Signed Tilings by Ribbon L n-Ominoes, n Even, via Gröbner Bases ()
Received 1 April 2016; accepted 26 July 2016; published 29 July 2016

1. Introduction
In this article, we study tiling problems for regions in a square lattice by certain symmetries of an L-shaped polyomino. Polyominoes were introduced by Golomb in [1] and the standard reference about this subject is the book Polyominoes [2] . The L-shaped polyomino we study is placed in a square lattice and is made out of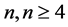 , unit squares, or cells (see Figure 1(a)). In a
, unit squares, or cells (see Figure 1(a)). In a 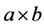 rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). They are ribbon L-shaped n-ominoes.
rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). They are ribbon L-shaped n-ominoes.
A ribbon polyomino [3] is a simply connected polyomino with no two unit squares lying along a line parallel to the first bisector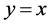 . We denote the set of tiles
. We denote the set of tiles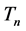 .
.
Related papers are [4] and [5] , investigating tilings by ![]() even. In [4] , we look at tilings by
even. In [4] , we look at tilings by ![]() in the particular case
in the particular case![]() . The starting point was a problem from recreational mathematics. We recall that a replicating tile is one that can make larger copies of itself. The order of replication is the number of initial tiles that fit in the larger copy. Replicating tiles were introduced by Golomb in [6] . In [7] , we study replication of higher orders for several tiles introduced in [6] . In particular, we suggested that the skewed L-tetromino showed in Figure 2(a) was not replicating of order
. The starting point was a problem from recreational mathematics. We recall that a replicating tile is one that can make larger copies of itself. The order of replication is the number of initial tiles that fit in the larger copy. Replicating tiles were introduced by Golomb in [6] . In [7] , we study replication of higher orders for several tiles introduced in [6] . In particular, we suggested that the skewed L-tetromino showed in Figure 2(a) was not replicating of order ![]() for any odd k. The question is equivalent to that of tiling a k-in- flated copy of the straight L-tetromino using only the ribbon orientations of an L-tetromino. The question is solved in [4] , where it is shown that L-tetromino is not replicating of any odd order. This is a consequence of a stronger result: a tiling of the first quadrant by
for any odd k. The question is equivalent to that of tiling a k-in- flated copy of the straight L-tetromino using only the ribbon orientations of an L-tetromino. The question is solved in [4] , where it is shown that L-tetromino is not replicating of any odd order. This is a consequence of a stronger result: a tiling of the first quadrant by ![]() always follows the rectangular pattern, that is, the tiling reduces to a tiling by
always follows the rectangular pattern, that is, the tiling reduces to a tiling by ![]() and
and ![]() rectangles, each tiled in turn by two tiles from
rectangles, each tiled in turn by two tiles from![]() .
.
The results in [4] are generalized in [5] to ![]() even. The main result shows that any tiling of the first quadrant by
even. The main result shows that any tiling of the first quadrant by ![]() reduces to a tiling by
reduces to a tiling by ![]() and
and ![]() rectangles. An application is the characterization of all rectangles that can be tiled by
rectangles. An application is the characterization of all rectangles that can be tiled by![]() , n even: a rectangle can be tiled by
, n even: a rectangle can be tiled by ![]() even, if and only if both sides are even and at least one side is divisible by n. The rectangular pattern persists if one adds an extra
even, if and only if both sides are even and at least one side is divisible by n. The rectangular pattern persists if one adds an extra ![]() tile to
tile to ![]() even. The new tiling set is denoted
even. The new tiling set is denoted![]() . A rectangle can be tiled by
. A rectangle can be tiled by ![]() if and only if it has both sides even. The main result also implies that a skewed L-shaped n-omino, n even, (see Figure 2(b)) is not a replicating tile of order
if and only if it has both sides even. The main result also implies that a skewed L-shaped n-omino, n even, (see Figure 2(b)) is not a replicating tile of order ![]() for any odd k. This development shows that the limitation of the orientations of the tiles can be of interest, in particular when investigating tiling problems in a skewed lattice.
for any odd k. This development shows that the limitation of the orientations of the tiles can be of interest, in particular when investigating tiling problems in a skewed lattice.
Signed tilings (see [8] ) are also of interest. These are finite placements of tiles on a plane, with weights +1 or −1 assigned to each of the tiles. We say that they tile a region R if the sum of the weights of the tiles is 1 for every cell inside R and 0 for every cell elsewhere. The existence of a regular tiling clearly implies the existence of a signed tiling. Many times solving a tiling problem can be reduced to a coloring argument. It was shown in [8] that the most general argument of this type is equivalent to the existence of a signed tiling. Consequently, different conditions for regular versus signed tilings can be used to show that certain tiling arguments are
![]()
Figure 1. (a) An Ln-omino with n-cells. (b) The set of tiles![]() .
.
![]()
Figure 2. (a) Skewed L-tetromino. (b) Skewed L n-omino.
stronger then coloring arguments. By looking at signed tilings of rectangles by ![]() and
and![]() , n even, we show that some of the results in [5] cannot be obtained via coloring arguments.
, n even, we show that some of the results in [5] cannot be obtained via coloring arguments.
A useful tool in the study of signed tilings is a Gröbner basis associated to the polynomial ideal generated by the tiling set. See Bodini and Nouvel [9] . One can associate to any cell in the square lattice a monomial in the variable x,y. If the coordinates of the lower left corner of the cell are (a, b), one associates![]() . This correspondence associates to any bounded tile a Laurent polynomial with all coefficients 1. The polynomial associated to a tile P is denoted
. This correspondence associates to any bounded tile a Laurent polynomial with all coefficients 1. The polynomial associated to a tile P is denoted![]() . The polynomial associated to a tile translated by an integer vector (c, d) is the initial polynomial multiplied by the monomial
. The polynomial associated to a tile translated by an integer vector (c, d) is the initial polynomial multiplied by the monomial![]() . If the region we tile is bounded and the tile set consists of bounded tiles, then the problem can be translated in the first quadrant via a translation by an integer vector, and one can work only with regular polynomials in x, y. See Theorem 10 below.
. If the region we tile is bounded and the tile set consists of bounded tiles, then the problem can be translated in the first quadrant via a translation by an integer vector, and one can work only with regular polynomials in x, y. See Theorem 10 below.
Signed tilings by ribbon L n-ominoes, n odd are studied in [10] , where we show that a rectangle can be signed tiled by ribbon L n-ominoes, n odd, if and only if it has a side divisible by n.
The main results of the paper are the following:
Theorem 1. A rectangle can be signed tiled by![]() , even, if and only if both sides of the rectangle are even and one of them is divisible by n, or one of the sides is odd and the other is divisible by
, even, if and only if both sides of the rectangle are even and one of them is divisible by n, or one of the sides is odd and the other is divisible by![]() .
.
Theorem 1 is proved in Section 5, after finding a Gröbner basis for ![]() even, in Section 3. A summary of Gröbner basis theory is shown in Section 2. Theorem 1 shows that some tiling results for
even, in Section 3. A summary of Gröbner basis theory is shown in Section 2. Theorem 1 shows that some tiling results for ![]() even, in [10] cannot be found via coloring arguments. We recall that it is shown in [4] that a rectangle is signed tiled by
even, in [10] cannot be found via coloring arguments. We recall that it is shown in [4] that a rectangle is signed tiled by ![]() if and only if the sides are even and one side is divisible by 4.
if and only if the sides are even and one side is divisible by 4.
Theorem 2. A rectangle can be signed tiled by ![]() if and only if both sides are even. A rectangle can be signed tiled by
if and only if both sides are even. A rectangle can be signed tiled by ![]() even, if and only if it has both sides even or one side is odd and the other side is divisible by
even, if and only if it has both sides even or one side is odd and the other side is divisible by![]() .
.
Theorem 2 is proved in Section 6, after finding a Gröbner basis for ![]() in Section 4. Theorem 2 shows that some tiling results for
in Section 4. Theorem 2 shows that some tiling results for ![]() even, in [5] cannot be found via coloring arguments.
even, in [5] cannot be found via coloring arguments.
Due to the Gröbner basis that we exhibit for ![]() even, we also have:
even, we also have:
Proposition 3. A k-inflated copy of the ribbon L n-omino, ![]() even, has a signed tiling by
even, has a signed tiling by ![]() if and only if k is even or k is odd and divisible by
if and only if k is even or k is odd and divisible by![]() .
.
The proof of Proposition 3 is shown in Section 7.
Barnes [11] [12] developed a method for solving signed tiling problems with complex number weights. Applied to our tiling sets, the method gives:
Theorem 4. If complex number weights are used, a rectangle can be signed tiled by ![]() even, if and only if it has a side divisible by n. If only integer weights are used, a rectangle that has a side divisible by n and all cells labeled by the same multiple of
even, if and only if it has a side divisible by n. If only integer weights are used, a rectangle that has a side divisible by n and all cells labeled by the same multiple of ![]() can be signed tiled by
can be signed tiled by ![]() even.
even.
Theorem 4 is proved in Section 8. A Gröbner basis for the tiling set helps even if Barnes method is used.
Theorem 5. If complex number weights are used, a rectangle can be signed tiled by ![]() even, if and only if it has an even side, and a rectangle can be signed tiled by
even, if and only if it has an even side, and a rectangle can be signed tiled by ![]() if and only if both sides are even.
if and only if both sides are even.
Theorem 5 is proved in Section 9. It is not clear to us if last statement in Theorem 4 implies Theorem 1 and if Theorem 5 implies Theorem 2. Guided by the work here, we conclude that Gröbner basis method for solving signed tiling problems with integer weights is sometimes more versatile and leads to stronger results then Barnes method.
The methods we use in this paper are well known when applied to a particular tiling problem. Here we apply them uniformly to solve an infinite collection of problems. Our hope was to see some regularity in the Gröbner bases associated to other infinite families of tiling sets, such as the family ![]() investigated in [5] . We recall that if
investigated in [5] . We recall that if ![]() are odd and n is even, tilings of the first quadrant by this family follow the rectangular pattern. Nevertheless, our hopes were not validated. The subfamily
are odd and n is even, tilings of the first quadrant by this family follow the rectangular pattern. Nevertheless, our hopes were not validated. The subfamily ![]() even, has a wide variety of Gröbner bases, making difficult to state a general result. Thus, for this particular family, we understand regular tilings of rectangles due to [5] , but cannot decide if the results follow from coloring invariants.
even, has a wide variety of Gröbner bases, making difficult to state a general result. Thus, for this particular family, we understand regular tilings of rectangles due to [5] , but cannot decide if the results follow from coloring invariants.
2. Summary of Gröbner Basis Theory
Let ![]() be the ring of polynomials with coefficients in a principal ideal domain (PID) R. A term in the variables
be the ring of polynomials with coefficients in a principal ideal domain (PID) R. A term in the variables ![]() is a power product
is a power product ![]() with
with![]() ; in particular
; in particular ![]() is a term. A term with an associated coefficient from R is called monomial. We endow the set of terms with the total degree-lexicographical order, in which we first compare the degrees of the monomials and then break the ties by means of lexicographic order for the order
is a term. A term with an associated coefficient from R is called monomial. We endow the set of terms with the total degree-lexicographical order, in which we first compare the degrees of the monomials and then break the ties by means of lexicographic order for the order ![]() on the variables. If the variables are only x, y and
on the variables. If the variables are only x, y and![]() , this gives the total order:
, this gives the total order:
![]() (1)
(1)
For ![]() we denote by HT(P) the leading term and by HM(P) the highest monomial in P with respect to the above order. We denote by HC(P) the coefficient of the leading monomial in P. We denote by T(P) the set of terms appearing in P and by M(P) the set of monomials in P. For a given ideal I in
we denote by HT(P) the leading term and by HM(P) the highest monomial in P with respect to the above order. We denote by HC(P) the coefficient of the leading monomial in P. We denote by T(P) the set of terms appearing in P and by M(P) the set of monomials in P. For a given ideal I in ![]() an associated Gröbner basis is introduced as in Chapters 5, 10 in [13] . If G is a finite set in
an associated Gröbner basis is introduced as in Chapters 5, 10 in [13] . If G is a finite set in![]() , we denote by I(G) the ideal generated by G in
, we denote by I(G) the ideal generated by G in![]() .
.
Definition 1. Let![]() . We say that f D-reduces to g modulo p and write
. We say that f D-reduces to g modulo p and write ![]() if there exists
if there exists ![]() with HM(p)/m, say m = mHM(p), and g = f ? mp. For a finite set Gin
with HM(p)/m, say m = mHM(p), and g = f ? mp. For a finite set Gin![]() , we denote by
, we denote by ![]() the reflexive-transitive closure of
the reflexive-transitive closure of![]() . We say that g is a normal form for f with respect to G if
. We say that g is a normal form for f with respect to G if ![]() and no further D-reduction is possible. We say that f is D-reducible modulo G if
and no further D-reduction is possible. We say that f is D-reducible modulo G if![]() .
.
If![]() , then
, then![]() . The converse is also true if G is a Gröbner basis.
. The converse is also true if G is a Gröbner basis.
Definition 2. A D-Gröbner basis is a finite set G of ![]() with the property that all D-normal forms modulo G of elements of I(G) equal zero. If
with the property that all D-normal forms modulo G of elements of I(G) equal zero. If ![]() is an ideal, then a D-Gröbner basis of I is a D-Gröbner basis that generates the ideal I.
is an ideal, then a D-Gröbner basis of I is a D-Gröbner basis that generates the ideal I.
Proposition 6. Let G be a finite set of![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
1) G is a Gröbner basis.
2) Every![]() , is D-reducible modulo G.
, is D-reducible modulo G.
We observe, nevertheless, that if R is only a (PID), the normal form associated to a polynomial f by a finite set G of ![]() is not unique. That is, the reminder of the division of f by G is not unique.
is not unique. That is, the reminder of the division of f by G is not unique.
We introduce now the notions of S-polynomial and G-polynomial that allows to check if a given finite set G of ![]() is a Gröbner basis for the ideal it generates. As usual, lcm is the notation for the least common multiple and gcd is the notation for the greatest common divisor.
is a Gröbner basis for the ideal it generates. As usual, lcm is the notation for the least common multiple and gcd is the notation for the greatest common divisor.
Definition 3. Let ![]() Let
Let ![]() with
with![]() , and
, and ![]() with
with![]() . The S-polynomial of
. The S-polynomial of ![]() is defined as:
is defined as:
![]() (2)
(2)
If ![]() such that
such that![]() . Then the G-polynomial of
. Then the G-polynomial of ![]() is defined as:
is defined as:
![]() (3)
(3)
Theorem 7. Let G be a finite set of![]() . Assume that for all
. Assume that for all ![]() and
and ![]() is top-D-reducible modulo G. Then G is a Gröbner basis.
is top-D-reducible modulo G. Then G is a Gröbner basis.
Assume now that R is an Euclidean domain with unique reminders (see page 463 [13] ). This is the case for the ring of integers Z if we specify reminders upon division by ![]() to be in the interval
to be in the interval![]() .
.
Definition 4. Let![]() . We say that f E-reduces to g modulo p and write
. We say that f E-reduces to g modulo p and write ![]() if there exists
if there exists ![]() with
with![]() , say
, say ![]() and
and ![]() where
where ![]() is the quotient of a upon division with unique reminder by
is the quotient of a upon division with unique reminder by![]() .
.
Proposition 8. E-reduction extends D-reduction, i.e., every D-reduction step in an E-reduction step.
Theorem 9. Let R be an Euclidean domain with unique reminders, and assume G subset of ![]() is a D-Gröbner basis. Then the following hold:
is a D-Gröbner basis. Then the following hold:
1) ![]() for
for![]() .
.
2) E-reduction modulo G has unique normal forms.
The following result connects signed tilings and Gröbner bases. See [9] and [14] for a proof.
Theorem 10. A polyomino P admits a signed tiling by translates of prototiles ![]() if and only if for some (test) monomial
if and only if for some (test) monomial ![]() the polynomial
the polynomial ![]() is in the ideal generated by
is in the ideal generated by![]() .
.
3. Gröbner Basis for Tn, n Even
We show first Gröbner bases for the ideals generated by![]() , as these are different from the general case.
, as these are different from the general case.
Proposition 11. The polynomials ![]() form a Gröbner basis for the ideal generated by
form a Gröbner basis for the ideal generated by![]() .
.
Proof. The polynomials corresponding to the tiles in ![]() are
are ![]() The last two can be generated by
The last two can be generated by![]() :
:
![]() (4)
(4)
It remains to show that the S-polynomial associated to ![]() can be reduced. One has:
can be reduced. One has:
![]() (5)
(5)
Proposition 12. A Gröbner basis for the ideal of polynomials generated by ![]() is given by:
is given by:
![]() (6)
(6)
Proof. The polynomials associated to ![]() are:
are:
![]() (7)
(7)
Similar to what is done in [10] the presence of ![]() in the Gröbner basis allows to reduce the algebraic proofs to combinatorial considerations. We leave most of the details of this proof to the reader. The proof that polynomials in Formula (7) are in the ideal generated by
in the Gröbner basis allows to reduce the algebraic proofs to combinatorial considerations. We leave most of the details of this proof to the reader. The proof that polynomials in Formula (7) are in the ideal generated by ![]() is similar to that of Proposition 5 in [10] . The proof that
is similar to that of Proposition 5 in [10] . The proof that ![]() are in the ideal generated by the polynomials in Formula (7) is similar to that of Proposition 6 in [10] . A geometric proof that
are in the ideal generated by the polynomials in Formula (7) is similar to that of Proposition 6 in [10] . A geometric proof that ![]() belongs to the ideal generated by
belongs to the ideal generated by ![]() is shown in Figure 3.
is shown in Figure 3.
For the rest of this section![]() . The polynomials associated to the tiles in
. The polynomials associated to the tiles in ![]() are:
are:
![]() (8)
(8)
We show that a Gröbner basis for the ideal generated by the polynomials in Formula (8) is given by:
![]()
Figure 3. The polynomial ![]() is generated by
is generated by![]()
![]() (9)
(9)
where ![]() is the integer part of x. It is convenient to visualize the elements of the basis as tiles with cells labeled by integers, see Figure 4.
is the integer part of x. It is convenient to visualize the elements of the basis as tiles with cells labeled by integers, see Figure 4.
Proposition 13. The polynomials ![]() belong to the ideal generated by
belong to the ideal generated by ![]()
Proof. Due to the symmetry, we only show that ![]() are in the ideal. The polynomials
are in the ideal. The polynomials ![]() allow to translate a horizontal domino with both cells labeled by the same sign, respectively a vertical domino, along a vector parallel to the line
allow to translate a horizontal domino with both cells labeled by the same sign, respectively a vertical domino, along a vector parallel to the line![]() . They also allow to translate horizontally or vertically a block of two cells adjacent at a vertex and labeled by different signs into a similar block. If the length of the translation is even, the signs stay the same. If the length of the translation is odd, all signs are changed. See Figure 5.
. They also allow to translate horizontally or vertically a block of two cells adjacent at a vertex and labeled by different signs into a similar block. If the length of the translation is even, the signs stay the same. If the length of the translation is odd, all signs are changed. See Figure 5.
We show how to build![]() . There are two cases to be considered, k odd and k even.
. There are two cases to be considered, k odd and k even.
The steps of a geometric construction for k odd are shown in Figure 6. To reach Step 1, we add several times multiples of![]() , as in Figure 5(b). To reach Step 2, we add several times multiples of
, as in Figure 5(b). To reach Step 2, we add several times multiples of![]() , as in Figure 5(a). To reach Step 3, first we subtract
, as in Figure 5(a). To reach Step 3, first we subtract![]() , then add several times multiples of
, then add several times multiples of ![]() as in Figure 5(c) and Figure 5(d). To obtain now
as in Figure 5(c) and Figure 5(d). To obtain now ![]() in the initial position, we multiply the tile in Step 3 by
in the initial position, we multiply the tile in Step 3 by![]() , which
, which
will translate the tile ![]() cells up, and then add multiples on
cells up, and then add multiples on![]() , as in Figure 5(c) and Figure 5(d).
, as in Figure 5(c) and Figure 5(d).
The steps of a geometric constructions for k even are shown in Figure 7. To reach Step 1, we add several times multiples of![]() , as in Figure 5(b). To reach Step 2, we add several times multiples of
, as in Figure 5(b). To reach Step 2, we add several times multiples of![]() , as in Figure 5(a). To reach Step 3, first we subtract
, as in Figure 5(a). To reach Step 3, first we subtract![]() , then add several times multiples of
, then add several times multiples of ![]() as in Figure 5(c) and Figure 5(d). To obtain now
as in Figure 5(c) and Figure 5(d). To obtain now ![]() in the initial position, we multiply the tile in Step 3 by
in the initial position, we multiply the tile in Step 3 by![]() , which will translate the tile
, which will translate the tile ![]() cells up, and then add multiples on
cells up, and then add multiples on![]() , as in Figure 5(c) and Figure 5(d).
, as in Figure 5(c) and Figure 5(d).
We show how to build![]() . There are two cases to be considered, k odd and k even.
. There are two cases to be considered, k odd and k even.
The steps of a geometric constructions for k odd are shown in Figure 8. To reach Step 1, we add several times multiples of![]() , as in Figure 5(b). To reach Step 2, we add several times multiples of
, as in Figure 5(b). To reach Step 2, we add several times multiples of![]() , as in Figure 5(a). To reach Step 3, first we subtract
, as in Figure 5(a). To reach Step 3, first we subtract![]() , then add several times multiples of
, then add several times multiples of ![]() as in Figure 5(c) and Figure 5(d). To obtain now
as in Figure 5(c) and Figure 5(d). To obtain now ![]() in the initial position, we multiply the tile in Step 3 by
in the initial position, we multiply the tile in Step 3 by![]() , which will translate the tile
, which will translate the tile ![]() cells up, and then add multiples on
cells up, and then add multiples on![]() , as in Figure 5(c) and Figure 5(d). The steps of a geometric constructions for k even are shown in Figure 9. To reach Step 1, we add
, as in Figure 5(c) and Figure 5(d). The steps of a geometric constructions for k even are shown in Figure 9. To reach Step 1, we add
several times multiples of![]() , as in Figure 5(b). To reach Step 2, we add several times multiples of
, as in Figure 5(b). To reach Step 2, we add several times multiples of![]() , as in Figure 5(a). To reach Step 3, first we subtract
, as in Figure 5(a). To reach Step 3, first we subtract![]() , then add several times multiples of
, then add several times multiples of ![]() as in Figure 5(c) and Figure 5(d). To obtain now
as in Figure 5(c) and Figure 5(d). To obtain now ![]() in the initial position, we multiply the tile in Step 3 by
in the initial position, we multiply the tile in Step 3 by![]() , which will translate the tile
, which will translate the tile ![]() cells up, and then add multiples on
cells up, and then add multiples on![]() , as in Figure 5(c) and Figure 5(d).
, as in Figure 5(c) and Figure 5(d).
Proposition 14. The polynomials ![]() belong to the ideal generated by
belong to the ideal generated by![]() .
.
Proof. Due to the symmetry, it is enough to show that ![]() and
and ![]() belong to the ideal. We show how to generate
belong to the ideal. We show how to generate ![]() (and consequently
(and consequently![]() ). To generate
). To generate ![]() we can reverse the process in Proposition 13. For
we can reverse the process in Proposition 13. For![]() , one has
, one has![]() . To generate
. To generate ![]() we first show how to obtain a configuration in which all nontrivial cells, 4 of them, are located on the main diagonal. See Figure 10. Then we use the tiles arithmetic shown in Figure 11 to pull the cells in positions
we first show how to obtain a configuration in which all nontrivial cells, 4 of them, are located on the main diagonal. See Figure 10. Then we use the tiles arithmetic shown in Figure 11 to pull the cells in positions ![]() and
and ![]() in positions
in positions ![]() and
and![]() . This gives
. This gives![]() .
.
Proposition 15. The sets ![]() and
and ![]() generate the same ideal.
generate the same ideal.
Proof. This follows from Propositions 13, 14.
Proposition 16. One has the following formulas:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
where![]() , which are given by D-reductions. Therefore,
, which are given by D-reductions. Therefore, ![]() form a Gröbner basis.
form a Gröbner basis.
Proof. We observe that we can always choose one of the coefficients ![]() in Definition 3 to be zero. So in order to check that we have a Gröbner basis, we do not need to use G-polynomials. Due to the symmetry, some formulas above follow immediately from others: (14) follows from (12), (15) follows from (11), (16) follows from (13), and second formula in (18) follows from the first. For the rest, note that the leading monomial in
in Definition 3 to be zero. So in order to check that we have a Gröbner basis, we do not need to use G-polynomials. Due to the symmetry, some formulas above follow immediately from others: (14) follows from (12), (15) follows from (11), (16) follows from (13), and second formula in (18) follows from the first. For the rest, note that the leading monomial in ![]() is
is![]() , the leading monomial in
, the leading monomial in ![]() is
is![]() , the leading monomial in
, the leading monomial in ![]() is
is![]() , the leading monomial in
, the leading monomial in ![]() is
is![]() , and the leading monomial in
, and the leading monomial in ![]() is
is![]() .
.
The D-reduction of ![]() is shown in Figure 12.
is shown in Figure 12. ![]() consists of two disjoint symmetric tiles. The reduction of them is similar and it is shown in parallel in Figure 12. We start with
consists of two disjoint symmetric tiles. The reduction of them is similar and it is shown in parallel in Figure 12. We start with
![]() (19)
(19)
The D-reduction of ![]() is shown in Figure 13. We start with
is shown in Figure 13. We start with
![]() (20)
(20)
From Step 3 to Step 4 we subtract ![]() or
or![]() , depending on k odd or even. From Step 4 to Step 5 we use the following formulas:
, depending on k odd or even. From Step 4 to Step 5 we use the following formulas:
![]() (21)
(21)
The D-reduction of ![]() is shown in Figure 14. We start with
is shown in Figure 14. We start with
![]() (22)
(22)
From Step 1 to Step 2 we subtract ![]() or
or![]() , depending on k odd or even. From Step 2 to Step 3 we use Formulas (21).
, depending on k odd or even. From Step 2 to Step 3 we use Formulas (21).
The D-reduction of ![]() is shown in Figure 15. We start with
is shown in Figure 15. We start with
![]() (23)
(23)
To reach Step 1, we subtract![]() . To reach Step 2, we subtract
. To reach Step 2, we subtract ![]() if k is
if k is
odd and ![]() if k is even. To reach Step 3, we add
if k is even. To reach Step 3, we add ![]() if k is odd and
if k is odd and
![]() if k is even.
if k is even.
The D-reduction of ![]() is:
is:
![]() (24)
(24)
The D-reduction of ![]() is:
is:
![]() (25)
(25)
4. Gröbner Basis for ![]() Even
Even
We consider first the case![]() .
.
Proposition 17. A Gröbner basis for the ideal generated by ![]() is:
is:![]() .
.
Proof. The pictures for tiles corresponding to the basis are shown in Figure 16. One has:
![]() (26)
(26)
thus the Gröbner basis can be generated by the polynomials in![]() . Conversely, one has:
. Conversely, one has:
![]() (27)
(27)
thus ![]() is generated by the Gröbner basis.
is generated by the Gröbner basis.
The S-polynomial ![]() is reduced as follows:
is reduced as follows:
![]() (28)
(28)
Let now![]() . Recall that
. Recall that ![]() is the set
is the set ![]() plus a
plus a ![]() tile with polynomial
tile with polynomial ![]() . We show that the Gröbner basis for the ideal generated by
. We show that the Gröbner basis for the ideal generated by ![]() is given by:
is given by:
![]() (29)
(29)
As ![]() is a subset of
is a subset of![]() ,
, ![]() generate the Gröbner basis
generate the Gröbner basis ![]() for
for![]() . Next formula shows how to generate
. Next formula shows how to generate![]() :
:
![]() (30)
(30)
Lemma 18. The polynomial ![]() is generated by
is generated by ![]() and
and![]() , and
, and ![]() is generated by
is generated by ![]() and
and![]() .
.
Proof. First produce![]() . Adding copies of this tile to
. Adding copies of this tile to ![]() gives the sum:
gives the sum:
![]() (31)
(31)
Expanding Formula (31) gives a telescopic sum that reduces to![]() .
.
Proposition 19. The polynomials ![]() belong to the ideal generated by
belong to the ideal generated by![]() .
.
Proof. We showed in Formula (30) how to generate![]() . By Lemma 18, we can start from
. By Lemma 18, we can start from ![]() to produce
to produce![]() . Then, subtract as follows:
. Then, subtract as follows:
![]() (32)
(32)
By the symmetry of ![]() about
about![]() , we can also generate
, we can also generate![]() . Combining the two:
. Combining the two:
![]() (33)
(33)
Finally, ![]() is produced from
is produced from ![]() and
and![]() , which we have from Formula (32):
, which we have from Formula (32):
![]() (34)
(34)
Lemma 20. The polynomials![]() ,
, ![]() ,
, ![]() belong to the ideal generated by
belong to the ideal generated by![]() .
.
Proof. We show below independently in Proposition 21 that ![]() is also in this ideal. Then one can easily check that:
is also in this ideal. Then one can easily check that:
![]() (35)
(35)
Proposition 21. The members of ![]() belong to the ideal generated by
belong to the ideal generated by![]() .
.
Proof. One has after calculations:
![]() (36)
(36)
To obtain![]() , begin with
, begin with
![]() (37)
(37)
By Lemma 18, this tile may be transformed into ![]() using only
using only![]() . We also get
. We also get ![]() by symmetry in the following way. Swap the variables
by symmetry in the following way. Swap the variables ![]() in Lemma 18. Then we have that
in Lemma 18. Then we have that ![]() and
and ![]() can each be produced from the other using either
can each be produced from the other using either![]() , which is symmetric about
, which is symmetric about![]() , or the tiles
, or the tiles![]() . Then swapping
. Then swapping ![]() in Formula (37) allows to obtain
in Formula (37) allows to obtain ![]() from the basis
from the basis![]() , which in turn can be obtained from the Gröbner basis itself by Lemma 20. Therefore the Gröbner basis also generates
, which in turn can be obtained from the Gröbner basis itself by Lemma 20. Therefore the Gröbner basis also generates![]() .
.
The polynomial ![]() can be used to change
can be used to change ![]() into
into![]() :
:
![]() (38)
(38)
By symmetry, the same process will change ![]() into
into ![]() using
using![]() . It remains, then, to show that the Gröbner basis for
. It remains, then, to show that the Gröbner basis for ![]() can generate
can generate ![]() and
and![]() . Start with
. Start with
![]() (39)
(39)
Then, multiply by ![]() and add
and add![]() :
:
![]() (40)
(40)
Once again, symmetry gives us a procedure for![]() , and the proof is complete.
, and the proof is complete.
Proposition 22. The sets ![]() and
and ![]() generate the same ideal.
generate the same ideal.
Proof. This follows from Propositions 19, 20.
Proposition 23. We have the following formulas:
![]() (41)
(41)
which are given by D-reductions. Therefore, ![]() forms a Gröbner basis.
forms a Gröbner basis.
Proof. We start with
![]() (42)
(42)
The reader may easily check that the given reductions are valid for these S-polynomials.
5. Proof of Theorem 1
The case ![]() follows as in paper [4] . We assume for the rest of this section
follows as in paper [4] . We assume for the rest of this section![]() . Consider a rectangle
. Consider a rectangle ![]() Using the presence of
Using the presence of ![]() and
and ![]() in the Gröbner basis, the rectangle can be reduced to one of the configurations in Figure 17(a) and Figure 17(b). Configuration (b) appears when
in the Gröbner basis, the rectangle can be reduced to one of the configurations in Figure 17(a) and Figure 17(b). Configuration (b) appears when ![]() are both even. The number of cells labeled by p is
are both even. The number of cells labeled by p is ![]() in a) and
in a) and ![]() in (b).
in (b).
In what follows the signed tile ![]() will play an important role. We recall that it can be moved horizontally/vertically as shown in Figure 5. The tile B does not belong to the ideal generated by
will play an important role. We recall that it can be moved horizontally/vertically as shown in Figure 5. The tile B does not belong to the ideal generated by![]() . Other signed tile of interest in the sequel is
. Other signed tile of interest in the sequel is![]() , which is the concatenation of a vertical bar of length n and B. The tile
, which is the concatenation of a vertical bar of length n and B. The tile ![]() belongs to the ideal generated by
belongs to the ideal generated by![]() .
.
Multiplying the polynomial associated to the rectangle by![]() , we can assume that the configurations in Figure 17 are at height
, we can assume that the configurations in Figure 17 are at height ![]() above the x-axis. Using the tiles
above the x-axis. Using the tiles ![]() and an amount of tiles B (p/2 if p is even and zero if p is odd), they can be reduced further to the configurations shown in Figure 17(c) and Figure 17(d). We observe that (b) is the sum of (a) with p/2 copies of B.
and an amount of tiles B (p/2 if p is even and zero if p is odd), they can be reduced further to the configurations shown in Figure 17(c) and Figure 17(d). We observe that (b) is the sum of (a) with p/2 copies of B.
Reducing further the configurations in Figure 17(c) and Figure 17(d), with copies of D, the existence of a signed tiling for the ![]() rectangle becomes equivalent to deciding when the following two conditions are both true:
rectangle becomes equivalent to deciding when the following two conditions are both true:
1) The polynomial ![]() divides:
divides:
![]() (43)
(43)
2) The extra tiles B that appear while doing tile arithmetic for 1), including those from Figure 17, can be cancelled out by![]() .
.
If![]() , then
, then![]() , so divisibility does not hold. If
, so divisibility does not hold. If![]() , we look at
, we look at ![]() as a sum of p polynomials with all coefficients equal to 1:
as a sum of p polynomials with all coefficients equal to 1:
![]() (44)
(44)
We discuss first 1) and show that it is true when p or q is divisible by n. Then, assuming this condition satisfied, we discuss 2).
1) Let![]() , and
, and![]() . The remainder
. The remainder ![]() of the division of
of the division of ![]() by
by ![]() is the sum of the remainders of the division of the p polynomials above by
is the sum of the remainders of the division of the p polynomials above by![]() .
.
If r is odd, one has the sequence of remainders, each remainder written in a separate pair of parentheses:
![]() (45)
(45)
If![]() , the sequence of remainders above is periodic with period n, given by the part of the sequence shown above, and the sum of any subsequence of n consecutive remainders is 0. So if p is divisible by n,
, the sequence of remainders above is periodic with period n, given by the part of the sequence shown above, and the sum of any subsequence of n consecutive remainders is 0. So if p is divisible by n, ![]() is divisible by
is divisible by![]() . If p is not divisible by n, then doing first the cancellation as above and then using the symmetry present in the sequence of remainders, the sum of the sequence of remainders equals 0 only if
. If p is not divisible by n, then doing first the cancellation as above and then using the symmetry present in the sequence of remainders, the sum of the sequence of remainders equals 0 only if![]() , that is, only if q is divisible by n.
, that is, only if q is divisible by n.
If r is even, one has the sequence of remainders, each remainder written in a separate pair of parentheses:
![]() (46)
(46)
If![]() , the sequence of remainders above is periodic with period n, given by the part of the sequence shown above, and the sum of any subsequence of n consecutive remainders is 0. So if p is divisible by n,
, the sequence of remainders above is periodic with period n, given by the part of the sequence shown above, and the sum of any subsequence of n consecutive remainders is 0. So if p is divisible by n, ![]() is divisible by
is divisible by![]() . If p is not divisible by n, then doing first the cancellation as above and then using the symmetry present in the sequence of remainders, the sum of the sequence of remainders equals 0 only if
. If p is not divisible by n, then doing first the cancellation as above and then using the symmetry present in the sequence of remainders, the sum of the sequence of remainders equals 0 only if![]() , that is, only if q is divisible by n.
, that is, only if q is divisible by n.
2) We assume now that n divides p or q and count the extra tiles B that appears. They are counted by the coefficients of the quotient, call it![]() , of the division of
, of the division of ![]() by
by![]() . We need to compute the sum
. We need to compute the sum ![]() of the coefficients in
of the coefficients in ![]() of the even powers of y and the sum
of the even powers of y and the sum ![]() of the coefficients in
of the coefficients in ![]() of the odd powers of y. The difference
of the odd powers of y. The difference ![]() gives the number of extra tiles B that we need to consider.
gives the number of extra tiles B that we need to consider.
We use the equation relating the derivatives:
![]() (47)
(47)
Note that![]() . Plugging in
. Plugging in ![]() gives:
gives:
![]() 48)
48)
Differentiating the equation of ![]() one has:
one has:
![]() (49)
(49)
While computing ![]() we recall that n is even and distinguish the following cases: Case A. p even, q odd, Case B. p odd, q even, Case C. p even, q even.
we recall that n is even and distinguish the following cases: Case A. p even, q odd, Case B. p odd, q even, Case C. p even, q even.
We need the following formulas:
![]()
![]()
![]() (50)
(50)
Case A. One has:
![]() (51)
(51)
The number of extra B tiles is![]() . To have a complete reduction, the number of B tiles has
. To have a complete reduction, the number of B tiles has
to be a multiple of![]() . As
. As ![]() and
and ![]() are relatively prime, p has to be a multiple of
are relatively prime, p has to be a multiple of![]() .
.
Case B. One has:
![]() (52)
(52)
The number of extra B tiles is![]() . We have the condition that q is a multiple of
. We have the condition that q is a multiple of![]() .
.
Case C. One has:
![]() (53)
(53)
The number of extra B tiles is ![]() In this case a signed tiling is always possible.
In this case a signed tiling is always possible.
6. Proof of Theorem 2
Let![]() . Consider a
. Consider a ![]() rectangle. Using the presence of
rectangle. Using the presence of ![]() and
and ![]() in the ideal, the rectangle can be reduced to one of the configurations in Figure 18, where the integers
in the ideal, the rectangle can be reduced to one of the configurations in Figure 18, where the integers ![]() represent the weights of the corresponding cells. The configuration in (a), and its copies appearing in (b), (c), (d), are multiples of
represent the weights of the corresponding cells. The configuration in (a), and its copies appearing in (b), (c), (d), are multiples of ![]() and can be reduced to zero. The remaining region in (b) can be reduced to
and can be reduced to zero. The remaining region in (b) can be reduced to![]() . As
. As ![]() is never a multiple of
is never a multiple of ![]() for
for![]() , this configuration can be reduced further by
, this configuration can be reduced further by ![]() to zero only if s is a multiple of
to zero only if s is a multiple of![]() . Same reasoning works for (c). The remaining region in (d) can be reduced further to
. Same reasoning works for (c). The remaining region in (d) can be reduced further to ![]() which is never a multiple of
which is never a multiple of![]() , thus cannot be reduced to zero.
, thus cannot be reduced to zero.
Assume now![]() . The proof is similar, but one observes that only configuration (a) in Figure 18 can be reduced to zero using the Gröbner basis for
. The proof is similar, but one observes that only configuration (a) in Figure 18 can be reduced to zero using the Gröbner basis for![]() .
.
7. Proof of Proposition 3
If k is even, finding a signed tiling for a -inflated copy of the Ln-omino can be reduced, via reductions by ![]() tiles, to finding a signed tiling for a
tiles, to finding a signed tiling for a ![]() rectangle. From Theorem 1 follows that such a tiling always exists. If k is odd, a reduction to a
rectangle. From Theorem 1 follows that such a tiling always exists. If k is odd, a reduction to a ![]() rectangle can be done only modulo a B tile, which does not belong to the ideal generated by
rectangle can be done only modulo a B tile, which does not belong to the ideal generated by![]() .
.
8. The Method of Barnes for ![]() Even
Even
In this section we give a proof of Theorem 4 following a method of Barnes. We assume familiarity with [11] [12] . We apply the method to ![]() even. Consider the polynomials (8) associated to the tiles in
even. Consider the polynomials (8) associated to the tiles in ![]() and denote by I the ideal generated by them. We show that the complex algebraic variety V defined by (8) consists only of the points
and denote by I the ideal generated by them. We show that the complex algebraic variety V defined by (8) consists only of the points![]() , where ε is an n-th root of identity different from 1.
, where ε is an n-th root of identity different from 1.
Separating x from![]() , replacing in
, replacing in ![]() and factoring the resulting polynomial gives:
and factoring the resulting polynomial gives:
![]() (54)
(54)
Denote the polynomial on the left hand side by![]() , and denote the corresponding polynomial in the variable x (obtained from
, and denote the corresponding polynomial in the variable x (obtained from ![]() and
and![]() ) by
) by![]() . Their roots are roots of unity of order
. Their roots are roots of unity of order ![]() and
and![]() . Using the system of equations that defines V, the roots of order
. Using the system of equations that defines V, the roots of order ![]() can be eliminated. Moreover, the only solutions of the system are as above.
can be eliminated. Moreover, the only solutions of the system are as above.
We show now that I is a radical ideal. We use an algorithm of Seidenberg which can be applied to find the radical ideal of a zero dimensional algebraic variety over an algebraically closed field. See Lemma 92 in [15] . Compare also with Theorem 7.1 in [11] . As V is zero dimensional, one can find square free polynomials ![]() and
and ![]() that belong to the radical ideal. We take these to be
that belong to the radical ideal. We take these to be ![]() where:
where:
![]() . (55)
. (55)
The ideal generated by![]() ’s and
’s and ![]() is radical. To show that I is radical, it is enough to show that
is radical. To show that I is radical, it is enough to show that ![]() belong to I. For
belong to I. For ![]() we have
we have ![]() and
and ![]() follows by symmetry.
follows by symmetry.
We apply Lemma 3.8 in [11] : a region R is signed tiled by ![]() if and only if the polynomial
if and only if the polynomial ![]() eva-
eva-
luates to zero on V. If R is a ![]() rectangle, then
rectangle, then ![]() which
which
evaluates to zero on V if and only if one of ![]() is divisible by n. This gives the first statement in Theorem 4.
is divisible by n. This gives the first statement in Theorem 4.
For the second statement in Theorem 4 we use the method described in the proof of Theorem 4.2 in [11] . A set of generators over the rationals for the rectangles that have a side divisible by n is given by the set ![]() and the polynomial with rational coefficients
and the polynomial with rational coefficients![]() . As
. As ![]() is already generated by H, this implies that
is already generated by H, this implies that ![]() multiples of the elements in H can signed tile with integer coefficients any
multiples of the elements in H can signed tile with integer coefficients any ![]() multiple of a rectangle with a side divisible by n.
multiple of a rectangle with a side divisible by n.
9. The Method of Barnes for ![]() Even
Even
Let![]() . Adding the extra polynomial
. Adding the extra polynomial ![]() to the set of generators, reduces the variety V to the point
to the set of generators, reduces the variety V to the point![]() . Proceeding as before, the ideal I is radical and the square free polynomials
. Proceeding as before, the ideal I is radical and the square free polynomials ![]() can be chosen to be
can be chosen to be![]() . The second one belongs to the Gröbner basis for
. The second one belongs to the Gröbner basis for ![]() and the first one can be generated as well as our set of generators
and the first one can be generated as well as our set of generators ![]() is symmetric in the variables
is symmetric in the variables![]() . The statement in Theorem 5 follows now from Lemma 3.8 in [11] .
. The statement in Theorem 5 follows now from Lemma 3.8 in [11] .
Assume now![]() . In this case the ideal I it is not radical. This follows using the theory developed in [11] about colorings. It is shown in [11] that
. In this case the ideal I it is not radical. This follows using the theory developed in [11] about colorings. It is shown in [11] that ![]() has 4 colorings, three standard and one nonstandard due to the differential operator
has 4 colorings, three standard and one nonstandard due to the differential operator![]() . It is easy to check that one of the standard colorings (see Figure 1 in [11] ) and the nonstandard coloring (see Figure 4 in [11] ) are the only colorings for
. It is easy to check that one of the standard colorings (see Figure 1 in [11] ) and the nonstandard coloring (see Figure 4 in [11] ) are the only colorings for![]() . One can check that a rectangle fits these colorings only if and only if it has both sides even, so it follows from Theorem 5.3 in [11] that a rectangle is signed tiled by
. One can check that a rectangle fits these colorings only if and only if it has both sides even, so it follows from Theorem 5.3 in [11] that a rectangle is signed tiled by ![]() if and only if it has both sides even.
if and only if it has both sides even.
10. Conclusions
Understanding tilings of rectangles by particular, even simple, polyominoes is a difficult combinatorial problem with a long history. Among the pioneering contributions, we mention those of Klarner [16] . In particular, Klarner on page 113 of [16] emphasizes the difficulty of the problem of classifying rectangles tileable by L-shaped n-ominoes of order two, that is, those for which two copies can be assembled in a rectangle: It seems impossibly difficult to characterize the rectangles which can be packed with an n-omino of order 2. A theorem of this kind restricted to the L-shaped n-ominoes of order 2 would probably still be too difficult to formulate.
Similar problems can be studied for parallelograms. As already mentioned in the introduction, the problem of tiling a general parallelogram positioned on a skewed lattice by all symmetries of a single skewed tile that has all sides parallel to the sides of the parallelogram is equivalent to the problem of tiling a rectangle by a polyomino (the straightened tile) allowing only a reduced set of orientations for that polyomino. This new problem seems to be more amenable to a solution and considerable progress has been done in the case of L-shaped n-ominoes of order two in several recent papers of one of the authors and collaborators [4] [5] [10] [17] . The results are consequences of more general tiling results for quadrants, showing that many of these tilings can be reduced to tilings by rectangles. Several general conjectures about the solution of this problem are formulated in [17] .
The main contribution of the present paper is a strengthening of the results in [5] . We show that the regular tiling results obtained in [5] for the tiling sets ![]() even, cannot be obtained from coloring invariants. The approach we used is via computations of explicit Gröbner basis for the ideals of polynomials generated by the tiling sets
even, cannot be obtained from coloring invariants. The approach we used is via computations of explicit Gröbner basis for the ideals of polynomials generated by the tiling sets ![]() even. In particular, we are able to classify signed tilings with integer weights of rectangles by
even. In particular, we are able to classify signed tilings with integer weights of rectangles by ![]() even. Our tools are graphic combinatorics and algebra. We also revisit some previous results of Barnes [11] [12] , relevant for signed tilings with complex/rational weights, and explain what they imply for
even. Our tools are graphic combinatorics and algebra. We also revisit some previous results of Barnes [11] [12] , relevant for signed tilings with complex/rational weights, and explain what they imply for![]() even.
even.
Acknowledgements
V. Nitica was partially supported by Simons Foundation Grant 208729. While working on this project, K. Gill was undergraduate student at West Chester University.