Study on a Ship with 6 Degrees of Freedom Inertial Measurement System and Related Technologies ()

Subject Areas: Oceanology

1. Introduction
The 6 DOF motion measurement technology has been a widespread concern in the industry. Due to the difficulty in finding a fixed point of reference, the real ship motion measurement is difficult in engineering, and the establishment of the line displacement is especially difficult. Feasible methods mainly include GPS and inertial measurement system, due to the current GPS accuracy is hard to meet the requirements. The research focused on the measured acceleration by inertial measurement system to reconstruct the ship displacement (linear displacement and angular displacement) [1] [2] .
Inertial measurement system can directly establish the ship heading and attitude, and in fact often needs the sway, surge and heave motion data, such as offshore supply, construction operations, aircraft etc. Strapdown inertial navigation system solves the problem of the traditional measurement platform system, and the measuring system has the advantage of light quality, small volume, low cost, long life and easy maintenance etc., and has been applied in practice [3] - [6] . In this paper, a new type of strapdown inertial navigation system is established, and an integral filtering algorithm is designed, which can reconstruct the ship line motion from the line acceleration and angular velocity measurement signals.
2. Coordinate System and the Posture Parameters of the Ship
The ship has 6 degrees of freedom movement, so first establish ship motion attitude coordinate system as shown in Figure 1, therefore, export express ship posture parameters, and then study the measuring method.
In the ship coordinate system, 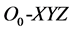 is coordinate system for inertial reference system,
is coordinate system for inertial reference system, 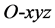 is ship carrier coordinates, O is a fixed point on the ship, Ox is parallel axis pointing to bow, point C is the particle of ship, the ship view as a rigid body, P is any point on the ship.
is ship carrier coordinates, O is a fixed point on the ship, Ox is parallel axis pointing to bow, point C is the particle of ship, the ship view as a rigid body, P is any point on the ship. 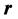 vector is from
vector is from 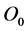 point to O point,
point to O point,  vector is from O point to P point,
vector is from O point to P point, 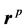 vector is from
vector is from  point to P point.
point to P point.
According to the definition of euler Angle, introducing coordinates  with new one to the attitude Angle
with new one to the attitude Angle  coordinates, and
coordinates, and 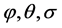 respectively for the roll Angle, pitching Angle and bow wave Angle, the ship swaying, surge and heave is the point C’s displacement in
respectively for the roll Angle, pitching Angle and bow wave Angle, the ship swaying, surge and heave is the point C’s displacement in . On the measuring point P at the ship, to establish the relationship between ship 6 degrees of freedom motion parameters and the measurement signal. According to Figure 1,
. On the measuring point P at the ship, to establish the relationship between ship 6 degrees of freedom motion parameters and the measurement signal. According to Figure 1,
 (1)
(1)
where ,
,  and
and  were compared with the vector inertial coordinate system
were compared with the vector inertial coordinate system![]() , this equation can also be described as,
, this equation can also be described as,
![]() (2)
(2)
The matrix A is the coordinate transformation matrix of coordinate system ![]() to coordinate system
to coordinate system![]() .
. ![]() vector in the vector coordinate
vector in the vector coordinate ![]() represented as
represented as ![]() vector. The formula (2) for one order guide, by the nature of the matrix,
vector. The formula (2) for one order guide, by the nature of the matrix, ![]() , this equation can also be described as,
, this equation can also be described as,
![]() (3)
(3)
The vector ![]() is the carrier coordinates with respect to the rotational angular velocity of
is the carrier coordinates with respect to the rotational angular velocity of ![]() inertial coordinate system
inertial coordinate system![]() , according to the principle of rigid body kinematics,
, according to the principle of rigid body kinematics,
![]() (4)
(4)
where
![]()
this Equation (4) can also be described as
![]() (5)
(5)
where ![]() is rotation angular velocity which is the carrier relative to the coordinate system
is rotation angular velocity which is the carrier relative to the coordinate system![]() , according to the equation
, according to the equation![]() , then
, then
![]() (6)
(6)
![]() (7)
(7)
where
![]() (8)
(8)
The Euler angles can be obtained by the formula of numerical integration. The seventh formula into formula (3) of the two order derivative,
![]() (9)
(9)
The Formulas (5) and Formulas (9) projects onto the carrier coordinates,
![]() (10)
(10)
![]() (11)
(11)
3. The Measurement Framework and Sensor Arrangement
In order to obtain the ship angular acceleration and sway, surge and heave parameter, taking the sensor layout as shown in Figure 2 the measurement system consists of 3 vertically mounted sensor group, each consisting of 1 angular velocity and acceleration sensor.
![]()
Figure 2. The sensor configuration for ship motion measurement.
According to the measurement scheme, firstly we can calculate the ship angular acceleration, taking into account the b in y and z direction of acceleration is not measured, so can be obtained,
![]() (12)
(12)
the same way for point a and c,
![]() (13)
(13)
![]() (14)
(14)
Therefore, the acceleration of the ship motion is obtained by the acceleration sensor and the angular rate gyro sensor. For ship swaying, surging and heaving motion parameters, it can be obtained by formula 9,
![]() (15)
(15)
![]() (16)
(16)
Therefore, as long as the acceleration angular velocity, angular acceleration of the ship and three axis are measured, we can calculate the ship sway, surge and heave acceleration.
4. Integral Filter Design Method
To design a second-order integration filter is the key to rebuilt displacement from the acceleration, and then determine the filter parameters. The ideal frequency response is,
![]() (17)
(17)
Two order integral filter design method includes the digital filter method and the frequency domain integral method. The finite impulse response (FIR) filter and infinite impulse response filter (IIR) digital filter has been widely used [7] [8] . Since the initial information of the IIR filter is needed to be measured, it is difficult to obtain the real ship, on the other hand, the FIR filter does not need the initial information of the measured object, but by choosing the appropriate filter parameters for two-order integral.
4.1. The Design of FIR Integration Filter
The design method of FIR filter includes maximum flatness and variational approximation. The main characteristic of maximum smoothness method is system filtering having best effect when near the angular frequency![]() , belonging to the band-pass filter, but it needs to estimate frequency in advance. The variational approximation method is transforming the two-order integral problem into an extremum problem,
, belonging to the band-pass filter, but it needs to estimate frequency in advance. The variational approximation method is transforming the two-order integral problem into an extremum problem,
![]() (18)
(18)
![]() ,
, ![]() ,
, ![]()
where ![]() is measured acceleration. It needs to solve a displacement function when it is transformed into functional problem,
is measured acceleration. It needs to solve a displacement function when it is transformed into functional problem,
![]() (19)
(19)
Obviously this is a boundary value problem, because it is difficult to measure the initial displacement and speed of the carrier, therefore, this function has no definite solution. For the ill posed problem, the regularization technique is used to estimate the solution in advance, and the reconstructed displacement is close to the given static displacement, because only the dynamic displacement can be reconstructed, the static equilibrium point can be set to zero. Then
![]() (20)
(20)
![]() is a regular function, r is determined solution domain, the regular conditional Equation (20) is introduced into the functional extremum problem in the form of penalty function.
is a regular function, r is determined solution domain, the regular conditional Equation (20) is introduced into the functional extremum problem in the form of penalty function.
![]() (21)
(21)
Functional extreme value problem formula (21) is called the Tikhonov regularization method, ![]() is a non negative regularization parameter. The larger the value of
is a non negative regularization parameter. The larger the value of ![]() is, the regular function have the greater the influence on the displacement solution, when
is, the regular function have the greater the influence on the displacement solution, when ![]() is zero, the Equation (21) become a boundary value problem. In the absence of the initial value, the equation is not solvable, the variation of functional problem Equation (21) is
is zero, the Equation (21) become a boundary value problem. In the absence of the initial value, the equation is not solvable, the variation of functional problem Equation (21) is
![]() (22)
(22)
The solution of this variational problem includes frequency domain and finite element method, etc. This paper uses the frequency domain method. According to the division of integral method,
![]() (23)
(23)
Then, functional extremum problem for control equations and boundary conditions are,
![]() (24)
(24)
![]()
Due to the displacement and velocity are unknowable at the boundary, so this paper uses the Newman boundary condition. Fourier transform of the Equation (24), and the transfer function of the control equation is
![]() (25)
(25)
where f is the frequency, ![]() represents the control equation of the transfer function, the displacement can be reconstructed by inverse Fourier transform,
represents the control equation of the transfer function, the displacement can be reconstructed by inverse Fourier transform,
![]() (26)
(26)
From the Equation (26) we can see that the low resistance filter does not need to be introduced in the displacement reconstruction, because the transfer function ![]() of the governing equation has the ability to suppress the low frequency noise.
of the governing equation has the ability to suppress the low frequency noise.
In order to determine the transfer function ![]() and the regularization parameter
and the regularization parameter![]() , the introduction of the normalized frequency
, the introduction of the normalized frequency![]() ,
, ![]() is the target frequency. The accuracy of the target frequency
is the target frequency. The accuracy of the target frequency ![]() is de-
is de-
fined as the control equation of the ratio of the transfer function and the ideal transfer function, then Equation (25) is related to the target frequency for normalization of transfer function
![]() (27)
(27)
The ratio between the transfer function of the control equation and the ideal transfer function ![]() is
is
![]() (28)
(28)
At the time of ![]() the precision function
the precision function![]() , precision to 0, when the frequency close to the target frequency, the precision function
, precision to 0, when the frequency close to the target frequency, the precision function ![]() rapid convergence to 1. At the time of
rapid convergence to 1. At the time of![]() , Precision function mainly depends on the regularization parameter values
, Precision function mainly depends on the regularization parameter values![]() . In the target frequency
. In the target frequency![]() , make
, make![]() , the accuracy at the target frequency is
, the accuracy at the target frequency is
![]()
So get regularization parameter values ![]() under certain precision
under certain precision
![]()
where![]() , then into Equation (27) and Equation (28),
, then into Equation (27) and Equation (28),
![]() (29)
(29)
![]() (30)
(30)
For different target accuracy![]() , control equation of the transfer function and the difference between ideal transfer function and accuracy function is shown in Figure 3 and Figure 4. When frequency is greater than the target, the control equation of the transfer function and the ideal transfer function almost unanimously, has
, control equation of the transfer function and the difference between ideal transfer function and accuracy function is shown in Figure 3 and Figure 4. When frequency is greater than the target, the control equation of the transfer function and the ideal transfer function almost unanimously, has
![]()
Figure 3. Comparison of transfer functions under different precision.
![]()
Figure 4. Comparison of accuracy functions under different precision.
nothing to do with the target accuracy, So the control equation of transfer function ![]() for signal reconstruc-
for signal reconstruc-
tion displacement; At the same time, the control equation of the transfer function can inhibit below target frequency acceleration signal, the signal is generally to measure noise and disturbance of constant value, the jamming signal frequency is lower, the transfer function of the noise suppression capability. The Figure 4 shows that the higher the accuracy of target, the transfer function of the lower noise suppression capability. As a result, precision of target and noise suppression ability between the two filter design index. The choice of target accuracy depends on the specific problem.
4.2. The Realization of FIR Integration Filter
The traditional FIR filter is similar to a given transfer function in frequency domain. Set the acceleration measurement time, every time the FIR filter can be expressed as
![]() (31)
(31)
where ![]() is FIR filter coefficient,
is FIR filter coefficient,![]() is displacement through the filter and the moment of t, time window width is
is displacement through the filter and the moment of t, time window width is![]() , the type of Fourier transform to Equation (31),
, the type of Fourier transform to Equation (31),
![]() (32)
(32)
![]() is the transfer function of the FIR filter,
is the transfer function of the FIR filter,
![]() (33)
(33)
Then,
![]() (34)
(34)
where ![]() is frequency,
is frequency, ![]() is the ratio of target frequency to sampling frequency. Control
is the ratio of target frequency to sampling frequency. Control
equation of the transfer function in frequency domain is even function. Because the control equation of the transfer function with increase rapidly declining, as shown in Figure 3, therefore, Equation (34) points in almost
has nothing to do with the integral upper limit![]() . So, it can be set
. So, it can be set![]() ,
, ![]() ,thus, the relation between
,thus, the relation between![]() ,
, ![]() and
and ![]() is independence. Although the number of FIR filter coefficients can be changed with the change of the filter order, when
is independence. Although the number of FIR filter coefficients can be changed with the change of the filter order, when ![]() is under certain circumstances, the filter coefficient
is under certain circumstances, the filter coefficient ![]() constant.
constant.
Gibbs phenomenon of high frequency oscillation occurs in the transfer function of FIR filter, in order to reduce the oscillation amplitude, filter order time should be enough big, smooth filter coefficients in p tends to k converge to zero. FIR filter, therefore, should be the last item on the coefficient of corresponds to the zero point,
![]() (35)
(35)
In general, select the rectangular window. Refactoring displacement can be used when no overlap or overlapping time window, corresponding to different displacement calculation strategy. In overlapping time window, will be calculated for each moment corresponding displacement, only will be a time window in central calculation result as the output, not the effect of overlapping time window boundary value estimation error will be reduced. Through the target cycle and the size of the window width defined filter
![]() (36)
(36)
where ![]() is expressed as a unit of time the filter size,
is expressed as a unit of time the filter size, ![]() is expressed as the filter size target cycle.
is expressed as the filter size target cycle.
Numerical analysis of Equation (34), ![]() and
and ![]() the relation curve between the zero return for 1.687 pe-
the relation curve between the zero return for 1.687 pe-
riod; The filter size relative to the initial three zero were 0.846, 4.22 and 7.594 times the target cycle; Due to the filter coefficient of zero in the first place not convergence, when![]() , a significant oscillating filter transfer function is; when
, a significant oscillating filter transfer function is; when ![]() and
and![]() , precision function of oscillation amplitude in the acceptable range. The larger the filter size, the smaller the oscillation amplitude of the precision function.
, precision function of oscillation amplitude in the acceptable range. The larger the filter size, the smaller the oscillation amplitude of the precision function.
Due to the symmetry of FIR filter coefficients, FIR filter transfer function can be expressed as
![]() (37)
(37)
FIR filter corresponding normalization transfer function and accuracy function is
![]() (38)
(38)
![]() (39)
(39)
5. Experimental Verification
The key of the problem is to reconstruct the line displacement from the acceleration measurement signal, the Oriental institute of vibration and noise control INV1601 vibration test system is adopted, the acceleration sensor is installed in the middle of the simple beam, the vibration acceleration of the beam is measured, and the displacement of the vibration of the beam is installed at the lower part of the measuring point. Reference sensitivity of piezoelectric accelerometer is 48.2 - 2 pC/m∙s−2. The test system shows in Figure 5.
The middle of the beam is subjected to harmonic excitation 5 Hz to 45 Hz, the acceleration sensor of laser displacement sensor sampling frequency and sampling frequency is 200 Hz. According to the accelerometer measurement signal, through FIR filter reconstruction beam displacement of measuring points, and compared with the laser displacement sensor measured displacement.
Vibration acceleration signal of a simply supported beam under 20 Hz excitation shows in Figure 6. The target frequency of the selected FIR filter is 20 Hz, the ratio between target frequency and sampling frequency is 0.1, the acceleration response reconstruction beam at the measuring point displacement. Reconstruction after partial details shows in Figure 7, there is no obvious phase lag between the output displacement and the actual displacement of the FIR filter, FIR filter reconstructed output displacement relative to the laser displacement sensor measurement more accurate the root mean square error (RMSE) is 0.004 mm, the mean value of the displacement peak value is 5.92%, close to the filter design accuracy is 97%, it shows that the FIR filter is designed to realize the second integral, reconstruct displacement from the acceleration signal, to the expected target design precision, and has certain ability of noise suppression.
![]()
Figure 6. The acceleration measurement signal of beam.
![]()
Figure 7. FIR filter reconstruction displacement.
6. Conclusions
A strap down inertial navigation attitude measurement system is established, and the integral filtering algorithm is used to measure the ship attitude and the three axis acceleration response; with the vibration of the beam simulation ship heaving, inverse displacement is measured by acceleration. The results of the study are as follows:
1) A strap down inertial measurement system for ship 6 degrees of freedom is established, sensor configuration technology is exported, measurement system is composed of three groups of vertical installation of sensors, and each group is made up of an angular rate and acceleration sensor.
2) The FIR integral filter is designed, and the design method of the filter parameters is studied to realize the goal of reconstructing the line displacement and angular displacement of the acceleration signal from the ship.
3) With the vibration of the beam simulation ship heaving, adopt the design of FIR filter, linear displacement from the accelerometer signal reconstruction, reconstruct displacement relative to the laser displacement sensor to measure the displacement of root-mean-square deviation of 0.004 mm, the displacement peak average error is 5.92%, close to the filter design precision being 97%.
4) The experimental results show that the 6 degree of freedom inertial measurement system and the FIR filter can effectively realize the reconstruction of the displacement from the acceleration signal and achieve the goal of the predetermined design precision. And it has certain ability of noise suppression.
5) Analysis shows that, in order to achieve a certain precision, the order of the filter is often high, the measurement system has a large amount of computation and memory cost.
Fund
This study is supported by the national science and technology major special sub task (2011ZX05056-003).