Weak Insertion of a Continuous Function between Two Comparable α-Continuous (C-Continuous) Functions ()

Subject Areas: Topology

1. Introduction
The concept of a C-open set in a topological space was introduced by E. Hatir, T. Noiri and S. Yksel in 1996 [1] . The authors define a set s to be a C-open set if , where u is open and A is semi-preclosed. A set s is a C-closed set if its complement is C-open set or equivalently if
, where u is open and A is semi-preclosed. A set s is a C-closed set if its complement is C-open set or equivalently if , where u is closed and A is semi-preopen. The authors show that a subset of a topological space is open if and only if it is an α-open set and a C-open set. This enable them to provide the following decomposition of continuity: a function is continuous if and only if it is α-continuous and C-continuous.
, where u is closed and A is semi-preopen. The authors show that a subset of a topological space is open if and only if it is an α-open set and a C-open set. This enable them to provide the following decomposition of continuity: a function is continuous if and only if it is α-continuous and C-continuous.
Recall that a subset A of a topological space  is called α-open if A is the difference of an open and a nowhere dense subset of X. A set A is called α-closed if its complement is α-open or equivalently if A is union of a closed and a nowhere dense set. Sets which are dense in some regular closed subspace are called semi-preopen or β-open. A set is semi-preclosed or β-closed if its complement is semi-preopen or β-open.
is called α-open if A is the difference of an open and a nowhere dense subset of X. A set A is called α-closed if its complement is α-open or equivalently if A is union of a closed and a nowhere dense set. Sets which are dense in some regular closed subspace are called semi-preopen or β-open. A set is semi-preclosed or β-closed if its complement is semi-preopen or β-open.
The concept of a set A was β-open if and only if 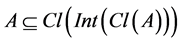 was introduced by J. Dontchev in 1998 [2] .
was introduced by J. Dontchev in 1998 [2] .
Recall that a real-valued function f defined on a topological space x was called A-continuous if the preimage of every open subset of 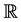 belongs to A, where A was a collection of subset of x and this the concept was introduced by M. Przemski in 1993 [3] . Most of the definitions of function used throughout this paper are consequences of the definition of A-continuity. However, for unknown concepts, the reader might refer to papers introduced by J. Dontchev in 1995 [4] , M. Ganster and I. Reilly in 1990 [5] .
belongs to A, where A was a collection of subset of x and this the concept was introduced by M. Przemski in 1993 [3] . Most of the definitions of function used throughout this paper are consequences of the definition of A-continuity. However, for unknown concepts, the reader might refer to papers introduced by J. Dontchev in 1995 [4] , M. Ganster and I. Reilly in 1990 [5] .
Hence, a real-valued function f defined on a topological space x is called c-continuous (resp. α-continuous) if the preimage of every open subset of 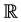 is c-open (resp. α-open) subset of x.
is c-open (resp. α-open) subset of x.
Results of Katĕtov in 1951 [6] and in 1953 [7] concerning binary relations and the concept of an indefinite lower cut set for a real-valued function, which was due to Brooks in 1971 [8] , were used in order to give necessary and sufficient conditions for the strong insertion of a continuous function between two comparable real-valued functions.
If g and f are real-valued functions defined on a space X, we write  in case
in case 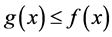 for all x in X.
for all x in X.
The following definitions were modifications of conditions considered in paper introduced by E. Lane in 1976 [9] .
A property p defined relative to a real-valued function on a topological space is a c-property provided that any constant function has property p and provided that the sum of a function with property p and any continuous function also has property p. If 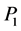 and
and 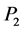 are c-property, the following terminology is used: A space x has the weak c-insertion property for
are c-property, the following terminology is used: A space x has the weak c-insertion property for 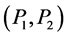 if and only if for any functions g and f on x such that
if and only if for any functions g and f on x such that  has property
has property  and f has property
and f has property , then there exists a continuous function h such that
, then there exists a continuous function h such that .
.
In this paper, it is given a sufficient condition for the weak c-insertion property. Also several insertion theorems are obtained as corollaries of this result.
2. The Main Result
Before giving a sufficient condition for insertability of a continuous function, the necessary definitions and terminology are stated.
Let ![]() be a topological space, the family of all α-open, α-closed, C-open and C-closed will be denoted by
be a topological space, the family of all α-open, α-closed, C-open and C-closed will be denoted by![]() ,
, ![]() ,
, ![]() and
and![]() , respectively.
, respectively.
Definition 2.1. Let a be a subset of a topological space![]() . Respectively, we define the α-closure, α-interior, C-closure and C-interior of a set a, denoted by
. Respectively, we define the α-closure, α-interior, C-closure and C-interior of a set a, denoted by ![]() and
and ![]() as follows:
as follows:
![]()
Respectively, we have ![]() are α-closed, semi-preclosed and
are α-closed, semi-preclosed and ![]() are α-open, semi-preopen.
are α-open, semi-preopen.
The following first two definitions are modifications of conditions considered in [6] [7] .
Definition 2.2. If ρ is a binary relation in a set S then ![]() is defined as follows:
is defined as follows: ![]() if and only if
if and only if ![]() implies
implies ![]() and
and ![]() implies
implies ![]() for any u and v in S.
for any u and v in S.
Definition 2.3. A binary relation ρ in the power set ![]() of a topological space x is called a strong binary relation in
of a topological space x is called a strong binary relation in ![]() in case ρ satisfies each of the following conditions:
in case ρ satisfies each of the following conditions:
1) If ![]() for any
for any ![]() and for any
and for any![]() , then there exists a set C in
, then there exists a set C in ![]() such that
such that ![]() and
and ![]() for any
for any ![]() and any
and any![]() .
.
2) If![]() , then
, then![]() .
.
3) If![]() , then
, then ![]() and
and![]() .
.
The concept of a lower indefinite cut set for a real-valued function was defined [8] as follows:
Definition 2.4. If f is a real-valued function defined on a space x and if ![]() for a real number
for a real number![]() , then
, then ![]() is called a lower indefinite cut set in the domain of f at the level
is called a lower indefinite cut set in the domain of f at the level![]() .
.
We now give the following main result:
Theorem 2.1. Let g and f be real-valued functions on a topological space x with![]() . If there exists a strong binary relation ρ on the power set of x and if there exist lower indefinite cut sets
. If there exists a strong binary relation ρ on the power set of x and if there exist lower indefinite cut sets ![]() and
and ![]() in the domain of f and g at the level t for each rational number t such that if
in the domain of f and g at the level t for each rational number t such that if ![]() then
then![]() , then there exists a continuous function h defined on X such that
, then there exists a continuous function h defined on X such that![]() .
.
Proof. Let g and f be real-valued functions defined on x such that![]() . By hypothesis there exists a strong binary relation ρ on the power set of x and there exist lower indefinite cut sets
. By hypothesis there exists a strong binary relation ρ on the power set of x and there exist lower indefinite cut sets ![]() and
and ![]() in the domain of f and g at the level t for each rational number t such that if
in the domain of f and g at the level t for each rational number t such that if ![]() then
then![]() .
.
Define functions F and g mapping the rational numbers ![]() into the power set of X by
into the power set of X by ![]() and
and![]() . If
. If ![]() and
and ![]() are any elements of
are any elements of ![]() with
with![]() , then
, then![]() , and
, and![]() . By Lemmas 1 and 2 of [7] it follows that there exists a function h mapping
. By Lemmas 1 and 2 of [7] it follows that there exists a function h mapping ![]() into the power set of X such that if
into the power set of X such that if ![]() and
and ![]() are any rational numbers with
are any rational numbers with![]() , then
, then ![]() and
and![]() .
.
For any x in x, let![]() .
.
We first verify that![]() : If x is in
: If x is in ![]() then x is in
then x is in ![]() for any
for any![]() ; since x is in
; since x is in ![]() implies that
implies that![]() , it follows that
, it follows that![]() . Hence
. Hence![]() . If x is not in
. If x is not in![]() , then x is not in
, then x is not in ![]() for any
for any![]() ; since x is not in
; since x is not in ![]() implies that
implies that![]() , it follows that
, it follows that![]() . Hence
. Hence![]() .
.
Also, for any rational numbers ![]() and
and ![]() with
with![]() , we have
, we have![]() . Hence
. Hence ![]() is an open subset of X, i.e., h is a continuous function on x.
is an open subset of X, i.e., h is a continuous function on x. ![]()
The above proof used the technique of proof of Theorem 1 of [6] .
3. Applications
The abbreviations ![]() and
and ![]() are used for α-continuous and c-continuous, respectively.
are used for α-continuous and c-continuous, respectively.
Corollary 3.1. If for each pair of disjoint α-closed (resp. c-closed) sets ![]() of X , there exist open sets
of X , there exist open sets ![]() and
and ![]() of X such that
of X such that![]() ,
, ![]() and
and ![]() then X has the weak c-insertion property for
then X has the weak c-insertion property for ![]() (resp.
(resp.![]() ).
).
Proof. Let g and f be real-valued functions defined on the X, such that f and g are ![]() (resp.
(resp.![]() ), and
), and![]() . If a binary relation ρ is defined by
. If a binary relation ρ is defined by ![]() in case
in case ![]() (resp.
(resp.![]() ), then by hypothesis ρ is a strong binary relation in the power set of x. If
), then by hypothesis ρ is a strong binary relation in the power set of x. If ![]() and
and ![]() are any elements of
are any elements of ![]() with
with![]() , then
, then
![]()
since ![]() is an α-closed (resp. c-closed) set and since
is an α-closed (resp. c-closed) set and since ![]() is an α-open (resp. c-open) set, it follows that
is an α-open (resp. c-open) set, it follows that ![]() (resp.
(resp.![]() ). Hence
). Hence ![]() implies that
implies that![]() . The proof follows from Theorem 2.1.
. The proof follows from Theorem 2.1. ![]()
Corollary 3.2. If for each pair of disjoint α-closed (resp. c-closed) sets![]() , there exist open sets
, there exist open sets ![]() and
and ![]() such that
such that![]() ,
, ![]() and
and ![]() then every α-continuous (resp. c-continuous) function is continuous.
then every α-continuous (resp. c-continuous) function is continuous.
Proof. Let f be a real-valued α-continuous (resp. c-continuous) function defined on the X. Set![]() , then by Corollary 3.1, there exists a continuous function h such that
, then by Corollary 3.1, there exists a continuous function h such that![]() .
. ![]()
Corollary 3.3. If for each pair of disjoint subsets ![]() of X , such that
of X , such that ![]() is α-closed and
is α-closed and ![]() is C-closed, there exist open subsets
is C-closed, there exist open subsets ![]() and
and ![]() of X such that
of X such that![]() ,
, ![]() and
and ![]() then x have the weak c-insertion property for
then x have the weak c-insertion property for ![]() and
and![]() .
.
Proof. Let g and f be real-valued functions defined on the X, such that g is ac (resp.![]() ) and f is
) and f is ![]() (resp. ac), with
(resp. ac), with![]() . If a binary relation ρ is defined by
. If a binary relation ρ is defined by ![]() in case
in case ![]() (resp.
(resp.![]() ), then by hypothesis ρ is a strong binary relation in the power set of X. If
), then by hypothesis ρ is a strong binary relation in the power set of X. If ![]() and
and ![]() are any elements of
are any elements of ![]() with
with![]() , then
, then
![]()
since ![]() is a c-closed (resp. α-closed) set and since
is a c-closed (resp. α-closed) set and since ![]() is an α-open (resp. c-open) set, it follows that
is an α-open (resp. c-open) set, it follows that ![]() (resp.
(resp.![]() ). Hence
). Hence ![]() implies that
implies that![]() . The proof follows from Theorem 2.1.
. The proof follows from Theorem 2.1. ![]()
Acknowledgements
This research was partially supported by Centre of Excellence for Mathematics(University of Isfahan).
NOTES
![]()
*This work was supported by University of Isfahan and Centre of Excellence for Mathematics (University of Isfahan).