Hardon-Quark Hybrid Stars Constructed by the Nonlinear σ-ω-ρ Mean-Field Model and MIT-Bag Model

Schun T. Uechi¹, Hiroshi Uechi²

¹Department of Physics & Astronomy, The University of Georgia, Athens, GA, USA.
²Osaka Gakuin University, Suita, Osaka, Japan.

DOI: 10.4236/oalib.1102012                

Abstract

Density-dependent relations among saturation properties of symmetric nuclear matter and hyperonic matter, properties of hadron-(strange) quark hybrid stars are discussed by applying the conserving nonlinear s-w-r hadronic mean-field theory. Nonlinear interactions that will be renormalized as effective coupling constants, effective masses and sources of meson equations of motion are constructed self-consistently by maintaining thermodynamic consistency to the mean-field approximation. The coupling constants expected from the hadronic mean-field model and SU (6) quark model for the vector coupling constants are compared; the coupling constants exhibit different density-dependent results for effective masses and binding energies of hyperons, properties of hadron and hadron-quark stars. The nonlinear s-w-r hadronic mean-field approximation with or without vacuum fluctuation corrections and strange quark matter defined by MIT-bag model are employed to examine properties of hadron-(strange) quark hybrid stars. The hadron-(strange) quark hybrid stars become more stable at high densities compared to pure hadronic and pure strange quark stars.

Keywords

Nonlinear σ-ω-ρ Mean-Field, Hyperon Onset Densities, Hyperon Coupling Ratios, Hadron-Quark Hybrid Stars

Subject Areas: Nuclear Physics, Nuclear Astrophysics, Many-Body Theory

1. Introduction

The symmetric nuclear matter is a self-bound matter whose binding energy exhibits a characteristic concave curve at saturation density, where pressure of nuclear matter vanishes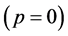. It has been known as a constraint to examine self-consistency to nuclear many-body approximations [1] - [3] . The self-consistency has been fundamental for many-body approximations in terms of Landau’s Fermi-liquid theory [4] - [6] , Kadanoff-Baym’s theory of conserving approximations [7] - [9] and the density functional theory [10] - [12] . The relativistic, field- theoretical, linear s-w mean-field approximations that maintain conditions of conserving approximations have been applied to finite nuclei, nuclear matter and neutron stars [13] [14] . These nuclear mean-field approximations reveal an important relation among self-consistent single particle energy, energy density and particle density, which is denoted as thermodynamic consistency [15] [16] . The conserving nonlinear s-w-r mean-field approximation which maintains thermodynamic consistency has been applied to investigate density-dependent correlations among properties of nuclear, neutron and hyperonic matter [17] - [19] . Thermodynamic consistency is important to derive consistent results for high energy and high density phenomena, such as heavy-ion collision, hypernuclei-formation experiments [20] and astrophysical phenomena [21] - [24] .

The nonlinear s-w-r mean-field approximation has several nonlinear coefficients whose values are determined by reproducing binding energy, symmetry energy and simultaneously searching the minimum value of incompressibility at saturation density, as well as reproducing a maximum mass of neutron stars at high density.

The binding energy at saturation is taken as −15.75 MeV at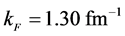, 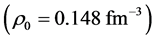with the symmetry energy, 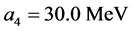in the current calculation [13] . The values of nonlinear coefficients which will produce effective masses of hadrons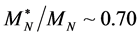, , 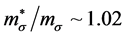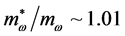and incompressibility, 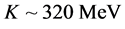, with symmetry energy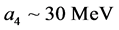, the maximum mass of neutron stars in b-equilibrium matter [23] , 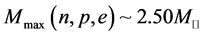(the solar mass: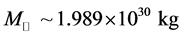), are found reasonable in the nonlinear s-w-r Hartree approximation [18] [19] .

The maximum masses of neutron stars are expected to be below 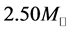[25] , or 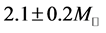[26] , which depend on the hadronic equation of state (EOS) for isospin asymmetric, hyperonic matter in the density range,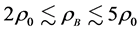. The hadronic liquid-gas phase transition at the surface of neutron stars and determination of the radius of smeared, gas-phase surface are not directly relevant to properties of hadronic matter and maximum masses of neutron stars. Hence, significant contributions to properties of neutron stars (mass, radius, moment of inertia…) come from hadronic EOS. The gas-phase equation of state which may exist on the surface of neutron stars produces negligible corrections and it is not relevant in the current hadronic analysis.

The nonlinear interactions exhibit significant density-dependent effects on incompressibility, K, and symmetry energy, 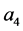, in high densities; these Fermi liquid properties monotonically increase about saturation density, but they are piecewise continuously softened at an hyperon onset density. These phenomena of piecewise continuous change of Fermi-liquid properties will be important for the analysis of Landau parameters, heavy-

ion collision, high energy and high density experiments. At a hyperon onset density from 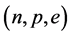to, the EOS suddenly becomes softer. This is because the nucleon Fermi energy, in the phase, will be redistributed to the hyperon Fermi energy, in the phase; consequently, the Fermi energies become relatively small in the phase compared with those of. The redistribution

and slow increase of Fermi energies appear whenever hyperons are generated, resulting in a softer equation of state and discontinuous changes of K and. This is numerically checked as discrete changes of physical quantities, such as effective masses of hadrons, incompressibility, symmetry energy and energy density [18] [19] .

Since the hyperon-onset confines Fermi-energies of baryons as explained above, single and double hyperon generations exhibit different density-dependent phenomena. For example, the -hyperon onset density such

as in - is; however, it gives when is generated in --. The same phenomena are observed with other hyperons, and generally the

onset-density of a hyperon is pushed up to a higher density, which is denoted as the push-up phenomena of hyperon onset-densities in many-fold hyperon generations [18] . Because of the push-up phenomena of the hyperon onset density, we have found that hyperon generations are confined at high densities and hyperons relevant to calculations of neutron stars are and. This is because hyperon generations make EOS softer and softer such that it is not possible to support observed maximum masses of neutron stars (shown in Section 4). The similar results are discussed in nonrelativistic Brueckner-Hartree-Fock [27] [28] and quark matter calculations [29] . The hyperon onset densities are related to hyperon single particle energies by way of phase equilibrium conditions. Hence, the Hugenholtz-Van Hove theorem and thermodynamic consistency at saturation of hyperon binding energy are essential to define self-consistent approximation of hyperonic matter. The single particle energies of nucleons and hyperons are important to study K and for magic nuclei [30] and hypernuclei [31] [32] .

Density-dependent effective masses and effective coupling constants, saturation properties for nucleons and hyperons are discussed in the nonlinear s-w-r mean-field approximation [18] [19] . The results shown that: 1) coupling constants of hyperons are related to those of nucleons by effective masses, effective coupling constants, binding energy at onset-density of respective hyperons. Hence, binding energies of symmetric nuclear matter and hyperon matter are self-consistently related to each other. 2) Self-consistency and density-dependent interactions may restrict hyperon generations at low densities, resulting in the push-up phenomena of hyperon onset densities. The suppression of hyperon generations is also discussed in different calculations [27] - [29] . 3) Coupling ratios of hyperons are expected to be, in order to be consistent with conditions of thermodynamic consistency, empirical values of nuclear matter and neutron stars. In the current calculations, we have included vacuum fluctuation corrections (VFC) into the nonlinear s-w-r approximation and examined properties of, , hyperonic matter, constrained by transitions to strange quark matter and properties of hadron-quark hybrid stars. The hadron-quark phase transitions are assumed to be a first order and computed by Maxwell construction [33] .

The conserving nonlinear s-w-r mean-field approximation [17] - [19] and quark-based effective nuclear models [34] [35] have been applied to finite nuclei, nuclear and isospin asymmetric, high-density matter. We have compared hyperon coupling constants required by the nonlinear s-w-r mean-field model with those required by SU(6) quark model for the vector coupling constants [36] [37] . The hyperon coupling constants required by hadronic and SU(6) quark models exhibit quite different results for effective masses, binding energies of hyperons [18] [19] and properties of hadron-quark hybrid stars. The coupling ratios required by SU(6) quark model cannot reproduce hyperon saturation properties, which will be discussed in terms of conditions of thermodynamic consistency in the Section 4. The analysis of discrepancies of predictions by hadronic and quark-based models may provide us with insight for constructing self-consistent nuclear many-body approximations [14] - [19] . The effective masses of hyperons depend on coupling ratios (, ,) and decrease analogous to effective masses of nucleons at high densities, which show strong density-dependent interactions. However, the effective masses of hyperons exhibit weak density-dependent results with required by SU(6) quark model for the vector coupling constants. In general, hadrons exhibit strong density- dependent interactions and correlations among properties of nuclear matter, hyperonic matter and neutron stars.

In the hadronic mean-field approximation, is preferred in order to be consistent with properties of nuclear matter and the maximum mass of neutron stars,. The value, , results in different effective masses and binding energies of hyperons; the discrepancies originate from density-depen- dent interactions of hadrons [19] .

The density-dependent many-body effects produced by the conserving nonlinear s-w-r mean-field approximation should be compared to chiral hadronic mean-filed approximations [38] - [41] . The effective quark-based chiral Lagrangian approach suggests that the appropriate in-medium scaling law,

, should be expected [42] . Although it is ambiguous whether

means that or at saturation density, they are certainly de- creasing above saturation density, since is model-independently expected to be decreasing. This is

significantly different from nonlinear mean-field approximations, since self-consistency of hadronic mean-field approximation demands [17] [43] and [44] at high densities. In other words, since effective masses and coupling constants are self-consistently related to each other, if some values decrease, the others have to counterbalance the variations. Therefore, all correlated effective masses and coupling constants must decrease or increase simultaneously in order to compensate for variations among others. At saturation density, effective masses of mesons are density-dependent and their ratios are approximately equal:. However, mesons exhibit different behaviors above saturation densities as explained. The discrepancy has been discussed in terms of thermodynamic consistency in the hadronic mean-field approximations [17] - [19] and should be investigated in other hadronic models to extract consistent model-independent results.

We have applied the nonlinear s-w-r mean-field approximation and MIT-bag model upon hadron-quark hybrid stars [23] [45] . The numerical analysis exhibits new results that the hadron-(strange) quark hybrid stars are more stable in high density than pure-hadronic and pure-strange quark stars. It suggests a relation between bag constant and QCD strong coupling constant, (B,) [46] [47] , to the central density and maximum mass of hadron-(strange) quark hybrid stars, (,). The results obtained in the current calculations should be examined from astronomical data whether or not hadron-quark stars are possible and the values of bag constant and strong coupling constant, (B,), could be consistent with astronomical data for neutron stars.

Self-consistent relations among saturation properties of nucleons and hyperons are briefly reviewed in Section 2. Quantitative numerical calculations for effective masses, onset densities and conditions of hyperon saturation are discussed in the articles [18] [19] . The MIT-bag quark matter and vacuum fluctuation correction to nonlinear mean-field approximation are explained in Section 3. Results of pure hadron and hadron-strange quark hybrid stars are discussed in Section 4; concluding remarks are in Section 5.

2. Self-Consistent Effective Masses and Coupling Constants in the Nonlinear s-w-r Mean-Field Approximation

The hadronic Lagrangian with nonlinear s-w-r interactions which yields density-dependent effective masses and coupling constants is given by [17] ,

(2.1)

where and denote the field of baryons and leptons, respectively. The meson-fields operators are: for the s-field, V for the vector-isoscalar w-meson, , and for r-meson. The vector field strengths, and, are defined as, and.

The coupled nonlinear quantum-field Lagrangian (2.1) is interpreted as baryon quantum-field Lagrangian in mean fields of mesons [13] . All dynamics generated by baryon fields are mediated by mean-fields of mesons which will be self-consistently defined in an approximation. The effective coupling constants, , denote renormalized, density-dependent coupling constants defined by self-consistent mean-field of s-meson. The nonlinear s-w-r mean-field model maintains the structure of Serot and Walecka’s linear s-w mean-field approximation [13] , Lorentz-invariance and renormalizability, the Hugenholtz-Van Hove theorem [2] , conditions of conserving approximations [7] - [12] , the virial theorem [15] [16] and Landau’s hypothesis of quasiparticles [4] - [6] . As we proved in the ref. [17] , nonlinear mean-field approximations are equivalent to Hartree approximation when nonlinear interactions are properly renormalized, and consequently, the concepts of effective masses and effective coupling constants are naturally generated by nonlinear mean-field interactions. Self-con- sistent relations among single particle energy, effective masses and coupling constants will restrict empirical values of low-density nuclear matter and high-density hadronic matter. The admissible values of effective coupling constants and masses are confined in certain values due to strong density-dependent correlations among physical quantities of nuclear matter and neutron stars [17] - [19] .

Meson-fields operators are replaced by mean-fields denoted by, , and. The equations of motion for baryons are given by,

(2.2)

where, and are effective coupling constants for, and mesons. One should notice that effective coupling constants cannot be simply introduced as external inputs to an employed approximation, since density-dependent coupling constants modify equations of motion for mesons. We self-consistently determine nucleon-meson coupling constants as density-dependent since we are interested in the density-dependent correlations among properties of symmetric nuclear matter. Nonlinear interactions are not assumed in the coupling constants for hyperons; effective masses of hyperons are defined by. The density-dependent nucleon-meson coupling constants that maintain thermodynamic consistency are,

(2.3)

The equations of motion for mesons are given by,

(2.4)

where is the total scalar source, the isoscalar density, and, the isovector density. The density-dependent coupling constants will modify the equation of motion for -meson which acquires a mass term, , and new source terms, from density-dependency of effective coupling constants.

The introduction of nonlinear -vertex interaction leads to the effective mass of nucleon:

(2.5)

and effective masses of nucleons and hyperons are related to each other as,

(2.6)

The total scalar source is obtained as,

(2.7)

where the scalar sources are respectively given by

(2.8)

and is the modified scalar density defined by; N is used to denote proton and neutron,; hyperons are denoted as,.

The w-meson and r-meson contributions to self-energies are given by

(2.9)

where the baryon-hyperon density, , is given by

(2.10)

and is the density-dependent ratio of hyperon-nucleon coupling constants. The self-energies, and, are briefly denoted as; the isovector density is denoted as where the Fermi momentum is for proton and for neutron [17] [18] . The isovector density, , and the ratios of sigma-nucleon coupling constants on r-meson are also defined;, where and.

Thermodynamically consistent effective masses of mesons compatible with effective coupling constants (2.3) are required to be:

(2.11)

Since effective masses of mesons and coupling constants depend on mean fields of mesons, they are density- dependent through meson fields. Note that the effective mass of s-meson depends on the scalar source of nucleons,. The modifications to equations of motion, propagators and self-energies produced by density-dependent effective coupling constants and masses are important for self-consistency.

The energy density, pressure of isospin-symmetric, asymmetric and charge-neutral hadronic matter are calculated by way of energy-momentum tensor, resulting in:

(2.12)

(2.13)

where is the Fermi-momentum; and are single particle energies for baryons and leptons, respectively. One can check that the thermodynamic relations, such as and the chemical potential, , are exactly satisfied with a given baryon density,.

The functional derivative of energy density, , with respect to the baryon number distribution, , is given by:

(2.14)

Thermodynamic consistency requires:, and [12] . Now, one can directly

prove that the self-energies calculated by propagators and the conditions of conserving approximations become equivalent, only if the effective masses and effective coupling constants of mesons are given by (2.3) and (2.11) [17] - [19] .

In order to start self-consistent hadronic matter calculations, nonlinear coupling constants, , , and other 9 nonlinear coefficients should be supplied; but admissible values of nonlinear coefficients are determined to satisfy properties of symmetric nuclear matter at saturation (−15.75 MeV at,), simultaneously searching for the minimum value of incompressibility and reproducing the maximum mass of isospin-asymmetric neutron stars. In addition, hadronic phase transitions from to should be carefully incorporated in EOS. The binding energies of hyperons required by hadronic model and SU(6) quark model for vector coupling constants [36] [37] are compared and discussed quantitatively in the articles [18] [19] .

3. The Nonlinear s-w-r Mean-Field Approximation with Vacuum Fluctuation Correction (VFC)

We have included vacuum fluctuation correction (VFC) into the nonlinear s-w-r mean-field approximation and applied the EOS with or without VFC to hadronic stars and hadron-quark hybrid stars. The EOSs for hadrons with VFC and quark matter generated by MIT-bag model are briefly discussed; based on the formalism, the pure hadronic and quark stars, stability of hadron-quark stars, are discussed in Section 4. The vacuum fluctuation corrections are explicitly performed with counter terms required by power-counting and the method of dimensional regularization [13] .

The self-energies with VFC in the conserving nonlinear s-w-r approximation are given with (2.7) by,

(3.1)

where, and for, since we are investigating effects of density-de- pendent interactions of nucleons; the density-dependent nonlinear self and mixing interactions among hyperons will be studied in the future. The self-energies and obtain no VFC in the mean-field approximation, which will be proven directly by dimensional regularization method. Note that it is also essential for an approximation with VFC to maintain conditions of conserving approximations in order to obtain (3.1).

The differences of VFC (3.1) given by the linear and nonlinear approximations appear by way of effective masses and effective coupling constants (2.3), (2.7), and (2.11). One will obtain the linear VFC correction by setting and in (3.1). It is essential to understand that equations of motion and self-consistency are rigorously satisfied with effective masses and effective coupling constants.

The energy density with VFC is obtained as,

(3.2)

Then, the total energy density is given with Equation (2.12) as,

(3.3)

The self-energies and pressure are also evaluated by dimensional regularization and thermodynamic consistency can be proved including VFC. As discussed in Section 2, all coupling constants have to be evaluated by maintaining properties at nuclear matter saturation, searching the minimum value of incompressibility. Incompressibility is and for (n, p, e) + VFC matter. The vacuum fluctuation corrections to nonlinear s-w-r mean-field approximation are not significant at low and high densities compared with those of nonlinear s-w-r self- and mixing-interactions.

Hadronic degrees of freedom give the most convenient description of EOS around nuclear matter saturation density, and at high densities where asymptotic freedom sets in, a quark description would be more natural. Hence, the hadronic equations of state obtained at the Section 2 and those of quark matter are combined as a two-phase model by assuming the first order phase transition from hadrons to quarks [17] [45] .

The energy density and pressure for quark matter given by MIT-bag model are obtained [45] - [47] :

(3.4)

(3.5)

where, , and B is the bag-constant (MeV/fm³); is the Fermi momen-

tum of flavor f. The energy density and pressure with the following given baryon density, charge neutrality and phase equilibrium conditions:

(3.6)

(3.7)

(3.8)

determine (u, d, s)-quark matter uniquely (note:). The thermodynamic potential for f to first order in the strong coupling constant is given by [23] [46] [47] :

(3.9)

where degeneracy. is the strong interaction coupling constant, and is the renormalization scale constant which is considered as a chemical potential of the problem and chosen as ~300 MeV [23] . However, the EOS of hadron-quark compact stars is not sensitive to the parameter, which is numerically checked and theoretically expected from (3.9) in high density region. It is suggested that EOS of quark matter interconnected with hadronic matter be mainly sensitive to parameters, in the current analysis. The expected value and restriction to can be numerically extracted from properties of hadron-quark matter and compact stars in the Section 4.

The energy density and pressure are now expressed as,

(3.10)

where and are chemical potential and particle distribution for the flavor f. The equations of state for hadronic and quark matter, phase transition conditions and TOV equation [21] are employed to calculate pure-hadron, pure-quark and hadron-quark compact stars.

4. The Properties of Hadronic and Hadron-Quark Hybrid Stars

We have applied the conserving nonlinear s-w-r mean-field approximation to examine properties of hadronic neutron stars and hadron-quark hybrid stars. The properties of pure hadronic stars are produced by employing hadronic equations of state, phase transition conditions, coupling ratios and TOV equation.

The masses v.s. central densities of hadronic stars produced by equations of state for -- matter are shown in Figure 1(a) and Figure 1(b). The solid line shows matter which produces the maximum mass of hadronic neutron stars, [18] , and LHA(n) (dot-dashed line) is the pure-neutron star calculated by the linear s-w mean-field approximation [13] . The arrows respectively indicate phase transitions from - and - matter.

The EOS of hadronic matter with generates the maximum mass (Figure 1(a)). However, the EOS with suggested by SU(6) quark model produces the small maximum mass of neutron stars: (Figure 1(b)), which is unable to support observed masses of neutron stars. The discrepancy calculated by and is clearly recognized by comparing the EOS and mass of neutron stars.

The properties of pure hadronic stars including VFC are shown in Figure 2(a) and Figure 2(b). The VFC effects are not so significant both in low and high densities compared with those of nonlinear many-body interactions. The difference of pressure and energy density in phase transition region is small (see arrows in Figure 2(a) and Figure 2(b)), which makes EOS smooth (see also Figure 1(a) and Figure 1(b)). Notice that the

(a) (b)

Figure 1. (a) Masses of hadronic neutron stars. Pure-neutron matter in linear s-w:. Isospin asymmetric b-equilibrium matter:. -- matter with the coupling ratios: (,) and (, ,) give; (b) Masses of hadronic neutron stars. -- matter with the coupling ratios: (,) and (, ,) give.

(a) (b)

Figure 2. (a) Hadronic neutron stars with VFC. -- matter with the coupling ratios: (,) and (, ,) give; (b) Hadronic neutron stars with VFC. -- matter with the coupling ratios: (,) and (, ,) give.

stable hadronic stars with are limited in the range of central energy density: , shown in bold, solid lines. The maximum masses are respectively , and for the coupling ratios, and. The maximum mass produced by SU(6) coupling ratios, and, is.

The EOS of pure-quark matter is used to calculate masses of pure-quark stars, which is shown in Figure 3. The bag constant should be, since normal nuclear matter becomes quark matter in the case of. The maximum masses of quark stars are , and . The MIT-bag model suggests that the stable quark stars with are limited in the range of bag constants, , and central energy densities:, shown in bold, solid lines in Figure 3.

The stable hadronic neutron stars with VFC and pure quark stars are shown in Figure 4, in order to remark energy-density regions of stable stars, respectively. The results of hadronic and quark stars in Figure 4 suggest that hadron-quark hybrid stars be possible about the central energy density, , since the EOS of quark matter could be energetically preferable in the high densities compared with that of hadrons. However, the overlap of central energy density between stable hadronic stars and pure-quark stars are very narrow. Hence, if the stable central energy densities are almost the same during H-Q phase transition, it indicates that hadron-quark stars would become unstable immediately [45] .

We assumed the first order hadron-quark phase transition, and solved phase transition conditions for chemical potential and pressure: and, by employing Maxwell construction. The TOV equation, hadronic and quark equations of state with phase transition conditions are applied to calculate properties of neutron stars. First, we have examined hadron-quark (H-Q) hybrid stars in case of + VFC and quark matter. The results are shown in Figure 5; the mass of H-Q stars is shown with a solid line, and the stable quark core is indicated by a dotted line. The results are not sensitive to the parameter in (3.9), which is checked numerically by changing. However, the H-Q stars are sensitive to the values of B and;, in order to produce observed masses of neutron stars:. This is because quark-EOS shifts to high energy densities if B is increased, which means that EOS becomes softer, resulting in compact stars with smaller mass and radius in high densities. In addition, if the QCD coupling constant is increased as, the masses of stable H-Q stars become small and shifted to high densities. Hence, appropriate values of B and to produce observed data of neutron stars in the current EOS are correlated to each other so that if B is increased, should be decreased, such as (,)

Figure 3. Masses of pure-quark stars with,. The stable pure-quark stars with are in.

Figure 4. Hadron stars with VFC and pure-quark stars. The stable hadronic stars are in.

Figure 5. Hadron-quark stars based on isospin asymmetric (n, p, e) + VFC matter. Note that the quark-core of H-Q stars is stable.

and (,). The property of in the analysis of hadron-quark infinite matter agrees with the results of bag-model fits to light-hadron spectra and renormalization group analyses in the paper by Farhi and Jaffe [47] .

Since H-Q stars are 2-phase compact stars (quark phase for star’s core and hadron phase for a mantle), the stability of H-Q stars should be reconsidered. The stability of pure hadronic and quark matter is examined respectively by the condition: [23] [48] . However, one should note that the stability criterion, , is for single phase compact stars, such as pure hadronic and quark stars.

The hadron-quark stars in Figure 5 show that the stable hadronic stars in the central energy range, , will undergo a phase transition (dotted horizontal line), reaching to H-Q stars. The total mass of H-Q stars decreases, but the stable quark-core will

develop. Therefore, it suggests that the H-Q star be stable, although the total mass of the star becomes smaller. Moreover, by comparing the stable energy densities of quark phase in Figure 4 with those of H-Q stars, it is found that the central energy density of stable H-Q stars is more extended for higher densities than that of single phase stars. It suggests that compact stars consisting of a mantle and a high density core be more stable than stars in a homogeneous single phase structure [47] [49] . When the QCD coupling constant, , increases, the H-Q phase transition density and quark-core will shift to higher densities, but the quark-core is stable and extended to higher densities. If the bag constant is small, such as, one will obtain a saturation curve (an inflection point for stability) within as in Figure 4, which suggests that the produced quark-core tends to become unstable.

The H-Q stars calculated with the EOS for -- + VFC to quark matter are shown in Figure 6(a) and Figure 6(b), respectively. The maximum masses in Figure 6(a) are and , whereas in Figure 6(b), and . A remarkable feature of H-Q stars in Figure 6(a) is that it can reasonably explain central energy densities and maximum mass configurations [26] for stable compact stars, ranging from.

In cases of the softer hadronic EOS in Figure 6(b) with and -correction, phase transitions occur in relatively low densities, resulting in smaller maximum masses of H-Q stars, , and hence, the EOS with the coupling constants may not be appropriate to explain observed masses of neutron stars. A physical reason from hadronic sector is clear in terms of EOS, but then, it is very interesting to investigate how hadronic and quark models reconcile problems pointed out in the paper.

If QCD coupling constant is set large, , in the soft EOS of Figure 6(b), the generation of quark-phase will move up to a very high density, further separating phase-transition energy densities of hadron and quark phases. In this case, stable hadron-quark stars produce masses much smaller than observed masses of neutron stars. Although more precise and detailed analyses are needed for many-body interactions of

(a) (b)

Figure 6. (a) Hadron-quark stars based on -- + VFC matter. The coupling ratios: (,) and (, ,); (b) Hadron-quark stars based on -- + VFC matter. The coupling ratios: (,) and (, ,).

hadronic and quark matter, the coupling constants for hadrons (or) suggested by SU(6) quark model would not be appropriate to examine properties of nuclear and hyperonic matter as well as maximum masses of high density compact stars.

5. Concluding Remarks

The quantum hadrodynamics (QHD) and mean-field approximations are useful for describing hadronic many- body systems at large distances, but they must ultimately break down at short distances where QCD is valid; hence, it is interesting to investigate how properties of hadron and quark dynamics will interconnect and influence each other dynamically [13] [14] . We applied the conserving nonlinear s-w-r mean-field approximation to study self-consistent, density-dependent interactions of hadrons and examined hadronic dynamics by employing coupling constants required from the QCD degrees of freedom. Discrepancies between hadronic and QCD predictions are explicitly shown by calculating masses of high density compact stars. The analysis is also applied to properties of nuclear matter, such as effective masses and effective coupling constants of nucleons, incompressibility and symmetry energy, saturation properties of hyperon binding energies [24] . The results may help understand predictions by effective hadronic and quark models as well as efficiencies and interrelations between models.

As saturation properties of symmetric nuclear matter are self-consistently related to those of hyperons, reproducing saturation properties of hyperons should be one of fundamental problems of nuclear many-body approximations. Although more quantitative and model-independent analyses are needed, it is concluded that hyperon coupling ratios required by SU(6) quark model for the vector coupling constants [36] [37] are not appropriate in order to generate saturation properties of hyperons. The coupling ratios of hyperons, , are appropriate to explain Fermi-liquid properties, saturation of hyperons [18] [19] and maximum masses of neutron stars. Discrepancies among hyperon coupling ratios and observables should be understood to improve calculations of effective models for hadrons.

Heavy-ion collision experiments as well as neutron stars are useful to examine validity of quark and hadronic models [50] [51] , since conditions of hadron-quark phase transition depend on both equations of state for hadronic and quark matter. The appropriate values of can be independently suggested from properties of infinite matter, which qualitatively support properties discussed in the paper [47] . The stable pure-hadronic stars and pure-quark stars based on MIT-bag model exist in different energy densities respectively, but if a first-order phase transition is assumed, the energy density of stable hadron-quark stars expands from 10¹⁴ to 10¹⁶

g/cm³. In the range of energy density, pure-hadron stars are less than, but H-Q stars are. It reasonably explains expected masses and energy density relations, [26] . Therefore,

existing high density compact stars are more likely to be regarded as hadron-quark stars rather than pure-hadron and pure-quark stars. These results should be further studied quantitatively by empirical data and effective theories of hadrons.

It is noteworthy that density-dependent many-body effects simulated by nonlinear s-w-r interactions are more important than those of vacuum fluctuation corrections (VFC). The contributions of VFC should be investigated further in more complicated nonlinear s-w-r HF, BHF approximations in order to study density-depen- dent and VFC corrections quantitatively. The role of chiral symmetry in hadronic models should be examined by extending the current nonlinear s-w-r mean-field approximation by including p-meson, which would help understand physical meaning and significance of chirality for hadronic and quark models.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Day, B.D. (1978) Current State of Nuclear Matter Calculations. Reviews of Modern Physics, 50, 495-521. http://dx.doi.org/10.1103/RevModPhys.50.495
[2]	Hugenholtz, N.M. and Van Hove, L. (1958) A Theorem on the Single Particle Energy in a Fermi Gas with Interaction. Physica, 24, 363-376. http://dx.doi.org/10.1016/S0031-8914(58)95281-9
[3]	Brueckner, K.A. and Levinson, C.A. (1955) Approximate Reduction of the Many-Body Problem for Strongly Interacting Particles to a Problem of Self-Consistent Fields. Physical Review, 97, 1344-1352. http://dx.doi.org/10.1103/PhysRev.97.1344 Brueckner, K.A. (1958) Single-Particle Energy and Effective Mass and the Binding Energy of Many-Body Systems, Single Particle Energies in the Theory of Nuclear Matter. Physical Review, 110, 597-600. http://dx.doi.org/10.1103/PhysRev.110.597 Brueckner, K.A. and Goldman, D.T. (1960) Single Particle Energies in the Theory of Nuclear Matter. Physical Review, 117, 207-213. http://dx.doi.org/10.1103/PhysRev.117.207 Brueckner, K.A., Gammel, J.L. and Kubis, J.T. (1960) Calculation of Single-Particle Energies in the Theory of Nuclear Matter. Physical Review, 118, 1438-1441. http://dx.doi.org/10.1103/PhysRev.118.1438
[4]	Landau, L.D. (1956) Theory of Fermi-Liquids. Soviet Physics JETP-USSR, 3, 920-925. Landau, L.D. (1957) Oscillations in a Fermi-Liquid. Soviet Physics JETP-USSR, 5, 101-108.
[5]	Pines, D. and Nozières, P. (1966) The Theory of Quantum Liquids. Addison-Wesley, Boston.
[6]	Nozières, P. (1964) Theory of Interacting Fermi Systems. Perseus Publishing, New York.
[7]	Baym, G. and Kadanoff, L.P. (1961) Conservation Laws and Correlation Functions. Physical Review, 124, 287-299. http://dx.doi.org/10.1103/PhysRev.124.287 Baym, G. (1962) Self-Consistent Approximations in Many-Body Systems. Physical Review, 127, 1391-1401. http://dx.doi.org/10.1103/PhysRev.127.1391
[8]	Takada, Y. (1995) Exact Self-Energy of the Many-Body Problem from Conserving Approximations. Physical Review, B52, 12708-12719. http://dx.doi.org/10.1103/PhysRevB.52.12708
[9]	Bonitz, M., Nareyka, R. and Semkat, D., Eds. (2000) Progress in Nonequilibrium Green’s Functions, Progress in Nonequilibrium Green’s Functions II. World Scientific, Singapore.
[10]	Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133. http://dx.doi.org/10.1103/physrev.140.a1133
[11]	Kohn, W. (1999) Nobel Lecture: Electronic Structure of Matter-Wave Functions and Density Functional. Reviews of Modern Physics, 71, 1253-1266. http://dx.doi.org/10.1103/RevModPhys.71.1253
[12]	Uechi, H. (2004) The Theory of Conserving Approximations and the Density Functional Theory in Approximations for Nuclear Matter. Progress of Theoretical Physics, 111, 525-543. http://dx.doi.org/10.1143/PTP.111.525
[13]	Serot, B.D. and Walecka, J.D. (1986) Advances in Nuclear Physics. Vol. 16, Negele, J.W. and Vogt, E., Eds., Plenum, New York.
[14]	Serot, B.D. (1992) Quantum Hadrodynamics. Reports on Progress in Physics, 55, 1855-1946. http://dx.doi.org/10.1088/0034-4885/55/11/001
[15]	Uechi, H. (1989) Fermi-Liquid Properties of Nuclear Matter in a Dirac-Hartree-Fock Approximation. Nuclear Physics A, 501, 813-834. http://dx.doi.org/10.1016/0375-9474(89)90162-0 Uechi, H. (1992) Landau Fermi-Liquid Theory and Approximations in the Quantum Hadrodynamical Model. Nuclear Physics A, 541, 397-412. http://dx.doi.org/10.1016/0375-9474(92)90183-K
[16]	Furnstahl, R.J. and Serot, B.D. (1991) Covariant Feynman Rules at Finite Temperature: Time-Path Formulation. Physical Review C, 44, 2141-2174. http://dx.doi.org/10.1103/PhysRevC.44.2141 Furnstahl, R.J. and Serot, B.D. (1990) Covariant Mean-Field Calculations of Finite-Temperature Nuclear Matter. Physical Review C, 41, 262-279. http://dx.doi.org/10.1103/PhysRevC.41.262
[17]	Uechi, H. (2006) Properties of Nuclear and Neutron Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation with Self- and Mixed-Interactions. Nuclear Physics A, 780, 247-273. http://dx.doi.org/10.1016/j.nuclphysa.2006.10.015 Uechi, H. (2008) Density-Dependent Correlations between Properties of Nuclear Matter and Neutron Stars in a Nonlinear σ-ω-ρ Mean-Field Approximation. Nuclear Physics A, 799, 181-209. http://dx.doi.org/10.1016/j.nuclphysa.2007.11.003
[18]	Uechi, S.T. and Uechi, H. (2009) The Density-Dependent Correlations among Observables in Nuclear Matter and Hyperon-Rich Neutron Stars. Advances in High Energy Physics, 2009, Article ID: 640919. http://dx.doi.org/10.1155/2009/640919
[19]	Uechi, H. and Uechi, S.T. (2009) Saturation Properties and Density-Dependent Interactions among Nuclear and Hyperon Matter. The Open Nuclear & Particle Physics Journal, 2, 47-60. http://dx.doi.org/10.2174/1874415X00902010047
[20]	Botvina, A.S. and Pochodzalla, J. (2007) Production of Hypernuclei in Multifragmentation of Nuclear Spectator Matter. Physical Review C, 76, Article ID: 024909. http://dx.doi.org/10.1103/PhysRevC.76.024909
[21]	Misner, C.W., Thorne, K.S. and Wheeler, J.W. (1973) Gravitation. W. H. Freeman and Company, New York.
[22]	Arnett, D. (1996) Supernovae and Nucleosynthesis. Princeton University Press, Princeton.
[23]	Glendenning, N.K. (2000) Compact Stars. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-1212-6
[24]	Uechi, H., Uechi, S.T. and Serot, B.D., Eds. (2012) Neutron Stars: The Aspect of High Density Matter, Equations of State and Related Observables. Nova Science Publisher, New York.
[25]	Akmal, A., Pandharipande, V.R. and Ravenhall, D.G. (1998) Equation of State of Nucleon Matter and Neutron Star Structure. Physical Review C, 58, 1804-1828. http://dx.doi.org/10.1103/PhysRevC.58.1804
[26]	Lattimer, J.M. and Prakash, M. (2007) Neutron Star Observations: Prognosis for Equation of State Constraints. Physics Reports, 442, 109-165. http://dx.doi.org/10.1016/j.physrep.2007.02.003
[27]	Vidaña, I., Polls, A., Ramos, A., Engvik, L. and Hjorth-Jensen, M. (2000) Hyperon-Hyperon Interactions and Properties of Neutron Star Matter. Physical Review C, 62, Article ID: 035801. http://dx.doi.org/10.1103/PhysRevC.62.035801
[28]	Baldo, M., Burgio, G.F. and Schulze, H.J. (2000) Hyperon Stars in the Brueckner-Bethe-Goldstone Theory. Physical Review C, 61, Article ID: 055801. http://dx.doi.org/10.1103/PhysRevC.61.055801
[29]	Maruyama, T., Chiba, S., Schulze, H.J. and Tatsumi, T. (2007) Hadron-Quark Mixed Phase in Hyperon Stars. Physical Review D, 76, Article ID: 123015. http://dx.doi.org/10.1103/PhysRevD.76.123015
[30]	Uechi, H. (2008) Correlations between Saturation Properties of Isospin Symmetric and Asymmetric Nuclear Matter in a Nonlinear σ-ω-ρ Mean-Field Approximation. Advanced Studies in Theoretical Physics, 2, 519-548.
[31]	Gal, A. (2003) To Bind or Not to Bind: ΛΛ Hypernuclei and Ξ Hyperons. Nuclear Physics A, 721, C945-C950. http://dx.doi.org/10.1016/S0375-9474(03)01248-X
[32]	Glendenning, N.K., Von-Eiff, D., Haft, M., Lenske, H. and Weigel, M.K. (1993) Relativistic Mean-Field Calculations of Λ and Σ Hypernuclei. Physical Review C, 48, 889-895. http://dx.doi.org/10.1103/PhysRevC.48.889
[33]	Bellac, M.L., Mortessagne, F. and Bartrouni, G.G. (2004) Equilibrium and Non-Equilibrium Statistical Thermodynamics. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511606571
[34]	Gelmini, G. and Ritzi, B. (1995) Chiral Effective Lagrangian Description of Bulk Nuclear Matter. Physics Letters B, 357, 431-434. http://dx.doi.org/10.1016/0370-2693(95)00924-A
[35]	Huguet, R., Caillon, J.C. and Labarsouque, J. (2007) Saturation Properties of Nuclear Matter in a Relativistic Mean Field Model Constrained by the Quark Dynamics. Nuclear Physics A, 781, 448-458. http://dx.doi.org/10.1016/j.nuclphysa.2006.11.046
[36]	Schaffner, J. and Mishustin, I.N. (1996) Hyperon-Rich Matter in Neutron Stars. Physical Review C, 53, 1416-1429. http://dx.doi.org/10.1103/PhysRevC.53.1416
[37]	Shao, G.-Y. and Liu, Y.-X. (2009) Influence of the σ-ω Meson Interaction on Neutron Star Matter. Physical Review C, 79, Article ID: 025804. http://dx.doi.org/10.1103/PhysRevC.79.025804
[38]	Furnstahl, R.J., Serot, B.D. and Tang, H.-B. (1997) A Chiral Effective Lagrangian for Nuclei. Nuclear Physics A, 615, 441-482. http://dx.doi.org/10.1016/S0375-9474(96)00472-1
[39]	McIntire, J., Hu, Y. and Serot, B.D. (2007) Loop Corrections and Naturalness in a Chiral Effective Field Theory. Nuclear Physics A, 794, 166-186. http://dx.doi.org/10.1016/j.nuclphysa.2007.08.008
[40]	Walecka, J.D. (1995) Theoretical Nuclear and Subnuclear Physics. Oxford University Press, Oxford.
[41]	Jha, T.K. and Mishra, H. (2008) Constraints on Nuclear Matter Parameters of an Effective Chiral Model. Physical Review C, 78, Article ID: 065802. http://dx.doi.org/10.1103/PhysRevC.78.065802
[42]	Brown, G.E. and Rho, M. (1991) Scaling Effective Lagrangians in a Dense Medium. Physical Review Letters, 66, 2720-2723. http://dx.doi.org/10.1103/PhysRevLett.66.2720
[43]	Chiapparini, M., Bracco, M.E., Delfino, A., Malheiro, M., Menezes, D.P. and Providência, C. (2009) Hadron Production in Non-Linear Relativistic Mean Field Models. Nuclear Physics A, 826, 178-189. http://dx.doi.org/10.1016/j.nuclphysa.2009.05.002
[44]	Uechi, H. and Uechi, S.T. (2008) Meeting Abstract. The Annual Meeting of Japan Physical Society, 63, Part 1, 49.
[45]	Serot, B.D. and Uechi, H. (1987) Neutron Stars in Relativistic Hadron-Quark Models. Annals of Physics, 179, 272-293. http://dx.doi.org/10.1016/0003-4916(87)90137-0
[46]	Chodos, A., Jaffe, R.L., Johnson, K., Thorn, C.B. and Weisskopf, V.F. (1974) New Extended Model of Hadrons. Physical Review D, 9, 3471-3495. http://dx.doi.org/10.1103/PhysRevD.9.3471
[47]	Farhi, E. and Jaffe, R.L. (1984) Strange Matter. Physical Review D, 30, 2379-2390. http://dx.doi.org/10.1103/PhysRevD.30.2379
[48]	Shapiro, S.L. and Teukolsky, S.A. (1983) Black Holes, White Dwarfs, and Neutron Stars. John Wiley & Sons Inc., Hoboken. http://dx.doi.org/10.1002/9783527617661
[49]	Witten, E. (1984) Cosmic Separation of Phases. Physical Review D, 30, 272-285. http://dx.doi.org/10.1103/PhysRevD.30.272
[50]	Dexheimer, V.A. and Schramm, S. (2009) Neutron Stars as a Probe for Dense Matter. Nuclear Physics A, 827, 579c-581c. http://dx.doi.org/10.1016/j.nuclphysa.2009.05.127
[51]	Bombaci, I., Logoteta, D., Panda, P.K., Providência, C. and Vidaña, I. (2009) Quark Matter Nucleation in Hot Hadronic Matter. Physics Letters B, 680, 448-452. http://dx.doi.org/10.1016/j.physletb.2009.09.039