Aggregation of Priorities in Multi-Criteria Decision Analysis (MCDA): Connecting Decision Spaces in the Cognitive Space ()
Received 7 June 2016; accepted 18 July 2016; published 21 July 2016

1. Introduction
In Multi-Criteria Decision Analysis (MCDA), often a complex decision problem is decomposed into a hierarchy of criteria, sub-criteria and alternatives. For such decomposition, one assumes that the decision about alternati- ves in respect of one criterion (or sub-criterion) can be made independent of decisions made in respect of other criteria (or sub-criteria). It also becomes easier for a decision maker (DM) to understand and analyze the decision hierarchy in small segments at a time. Finally, results (i.e., criteria and sub-criteria weights and alternative priorities) from different segments are aggregated. Integrated values for the decision alternatives can be presented as aggregate scores, normalised relative priorities or ordinal ranks. In this paper, we consider a simple three level hierarchy without any loss of generality. The top level represents the overall goal of the decision. The second level represents the criteria, and the third level is for a list of alternatives. The criteria are characterised by weights that may sum to one. The priorities of the alternatives under each criterion may be expressed as un-normalised preference scores or relative priorities that are normalised such that they sum to one. The preference scores or the relative priorities are often derived from a Multi-Criteria Decision Model (MCDM). Finally, the criteria weights and alternative priorities are aggregated to generate an overall rating for alternatives.
In addition, based on recursion relations that link two decision spaces having an added or deleted alternative, we introduce the concept of cognitive space spanning multiple decision spaces or scenarios. We present arguments for expanding the usual modelling experiences beyond a particular decision space into the cognitive space. Expanded modelling will help us detect shortcomings if any, of models developed on a particular decision space. In Section 2, we outline the new contributions of this paper. We provide a generalised derivation of a modified aggregation rule, further discuss recursion relations and overview the meaning of weights in this context. Section 3 and Section 4 demonstrate the use the new aggregation rule in the AHP with numerical examples. Section 5 delineates the concept of expanded analytical modelling in cognitive space and conclusions are made in Section 6.
2. Representation of the Generalised Decision Space and Formulation of the Modified Aggregation Rule
In this section, starting from a generalised multi-criteria decision space, a modified aggregation rule is derived and contrasted with the familiar WSM. Calculations involve combining measurements from two different spaces (i.e., criteria space and alternative space), each having different units of scale and may have different dimensions, too. However, no mathematical derivation for the WSM which represents a complex measurement procedure is available in the MCDA literature. Perhaps, the formula was introduced as a simple extension of the expected value formula with the normalised weights replacing probabilities. The earlier work [7] also started with the WSM and modified it to incorporate norms of the priority vectors. The new contributions in this paper include a formal mathematical derivation of the modified weighted sum method showing how the norms of priority vectors naturally appear in formal mathematics spanning the criteria and alternative spaces. The other contribution is the discussion of cognitive space that connects multiple decision spaces, each represented by a set of criteria and alternatives. This approach helps us to project the rank reversal problem as a cognitive issue in the context of an expanded analytic modelling framework. As an alternative is added or deleted, the logical connections between decision spaces are also analysed later in this section in terms of the recursion rules. In the end, we discuss the impact of normalisation of criteria weights whose meanings are further reviewed in reference to earlier MCDA research.
2.1. Modified Weighted Sum Aggregation Rule from the Generalised Decision Space
We consider a decision space with n alternatives judged with respect to m criteria as represented by the hierarchy diagram in Figure 1. The criteria and alternatives constitute two distinct spaces, S(C) and S(A) respectively. S(C) is m dimensional and S(A) is n dimensional vector spaces spanned by a set of orthonormal basis vectors αi, (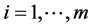 ) and βj, (
) and βj, ( ) respectively where the basis vectors are just column vectors of dimension m and n respectively,
) respectively where the basis vectors are just column vectors of dimension m and n respectively,
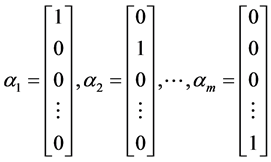

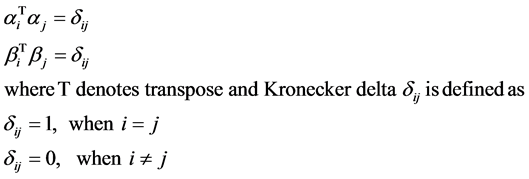 (1)
(1)
Let us assume that the criteria weights (implying the relative importance of the criterion) can be obtained from any available technique. We develop formulations of this section independent of any particular model (e.g.,
AHP). We represent the weights by a vector w and for the sake of convenience we assume that the weights are normalised such that they sum to one. The rest of the discussions in this section will not change even if the weights are not normalised (in that case weights will be a constant multiple of the normalised ones). So, the weight vector w is,
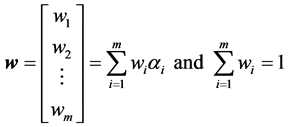 (2)
(2)
Similarly, with respect to ith criterion, let the priority vector for n alternatives be
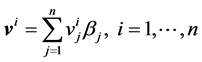 (3)
(3)
The priority vectors vi can be obtained in various ways subject to a decision model. For example, it can represent a set of scores as obtained from a decision maker’s mental model or it can be obtained from the pairwise comparison matrix (Pi) as in the AHP. If one employs the eigenvector method in the AHP, then it can be just an eigenvector (not necessarily normalised) derived from the eigenvalue equation,
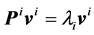 (4)
(4)
If ui is the corresponding normalised priority vector, then
 (5)
(5)
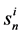 is the norm of the unnormalised priority vector with n alternatives with respect to the ith criterion. In the scoring method,
is the norm of the unnormalised priority vector with n alternatives with respect to the ith criterion. In the scoring method, 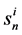 is known, but in the AHP it is unknown.
is known, but in the AHP it is unknown.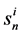 , the norm of n-dimensional priority vector sets the unit of scale for the normalised priority vector uij and can vary for different criteria. Therefore, the correct aggregation rule should incorporate
, the norm of n-dimensional priority vector sets the unit of scale for the normalised priority vector uij and can vary for different criteria. Therefore, the correct aggregation rule should incorporate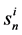 .
.
The combined decision space D is a direct product of the criteria space and the alternative space, i.e.,
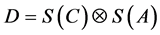
Thus, the priority state y is derived from a direct product of w and vi s so that it preserves the hierarchic structure of Figure 1. We compute the sum of the direct products of the orthogonal components of w in the criteria space with the corresponding priority vectors under each criterion. That is,
![]() (6)
(6)
![]()
Figure 2. Generating priority vector from DM’s preference inputs.
Please note that the column vectors αi s are defined in m dimensional criteria space and vi s are defined in the n-dimensional alternative space.
It is worth pointing out that, in general, there are arbitrary constants multiplying each term in the expansion of Equation (6). For convenience, we absorbed them in vi s and thus in the corresponding norms![]() . Therefore, the norms that set the scale of normalisation are also arbitrary at this stage. It is the decision maker who eventually sets values for the norms as it will be explained later in the text when we discuss the computational algorithm and the numerical example.
. Therefore, the norms that set the scale of normalisation are also arbitrary at this stage. It is the decision maker who eventually sets values for the norms as it will be explained later in the text when we discuss the computational algorithm and the numerical example.
Now expanding vi s in terms of the basis vectors βj given in Equation (3), we finally have,
![]() (7)
(7)
We project out the intensity of priority corresponding to the pth state of the criteria space and the qth basis state of the alternative space by multiplying on the left by ![]() and
and![]() ,
,
![]() (8)
(8)
In additive models, we sum over all criteria to obtain the aggregate priority Rq of alternative q,
![]() (9)
(9)
Now, using the relation between the unnormalised local priority ![]() and the normalised ones
and the normalised ones ![]() of Equation (5), we have
of Equation (5), we have
![]() (10)
(10)
The normalised aggregate priority rq (i.e.,![]() ) for the qth alternative is given by a Modified Aggregation Rule (MAR),
) for the qth alternative is given by a Modified Aggregation Rule (MAR),
![]() (11)
(11)
The above expression should be compared with the traditional weighted sum formula called Simple Aggregation Rule (SAR),
![]() (12)
(12)
The MAR was proposed as the correct aggregation procedure for obtaining overall priorities in [7] . It is worth pointing out at this stage that if the weight vector was not normalised (i.e., if in Equation (6) we used un-norma- lised weights Wp), we would have
![]() (13)
(13)
It is straightforward to check that the expression of the normalised aggregate priority rq in Equation (11) would remain the same confirming that we did not sacrifice any generality by considering a normalised weight vector at the very beginning in Equation (6).
It should be further noted that the proposed aggregation rule (MAR) becomes identical with the familiar weighted sum rule (SAR) only when norms of all priority vectors are equal (i.e.,![]() ). This implies a common unit of scale used to normalise the local priority vectors under all criteria. A similar general structure of decision space was earlier considered in [8] for developing the AHP in the Euclidean space where a common unit of scale was considered and thus lacked a general rule of aggregation.
). This implies a common unit of scale used to normalise the local priority vectors under all criteria. A similar general structure of decision space was earlier considered in [8] for developing the AHP in the Euclidean space where a common unit of scale was considered and thus lacked a general rule of aggregation.
The above result is independent of decision models that one would use to derive values for the alternative priority vectors. For example, Saaty [4] [5] developed an ingenious mechanism based on reciprocal pairwise comparison matrices and an eigenvalue equation for deriving the normalised local priorities in the AHP. Values for ![]() are unavailable. Thus, it used the familiar weighted sum rule (SAR) for aggregation, assuming same unit of scale for local priorities under all criteria causing rank reversals when it should not.
are unavailable. Thus, it used the familiar weighted sum rule (SAR) for aggregation, assuming same unit of scale for local priorities under all criteria causing rank reversals when it should not.
2.2. Recursion Rules
Two recursion rules used in [7] for the rank reversal analysis are re-stated below (can be derived easily following the same procedure with a slight change in notations).
1) When a new alternative (i.e., the (n + 1)th alternative) is added to the decision space (the primed items refer to the corresponding quantities in the new decision space with n + 1 alternatives), in a fully consistent case,
![]() (14)
(14)
![]() (15)
(15)
2) When an existing alternative (i.e., the nth alternative) is deleted from the decision space (the primed items refer to the corresponding quantities in the new decision space with n − 1 alternatives), in a fully consistent case,
![]() (16)
(16)
![]() (17)
(17)
Using the MAR, it can be proved [7] that ratio of two aggregate priorities for alternatives is preserved when a new alternative is added or an existing one is deleted (see Appendix A).
2.3. Meaning of Criteria Weights in the Modified Aggregation Rule
In MCDA research, it has been noted [10] that the most widely used and the simplest aggregation method is the weighted sum method (WSM). Considering n alternatives and m criteria, the aggregate preference Pi of alternative Ai (![]() ) is calculated according to the Formula (3)]:
) is calculated according to the Formula (3)]:
![]()
where, W j is the weight of the jth criteria. Here, ![]() s can be normalised (i.e.,
s can be normalised (i.e.,![]() ) or W j s can be norma- lised (i.e.,
) or W j s can be norma- lised (i.e.,![]() ) or both can be normalised. In the discussion following Equation (13), it is explained that
) or both can be normalised. In the discussion following Equation (13), it is explained that
the normalisation of weights does not affect the MAR that is being proposed here as the correct aggregation method as it prevents rank reversals. But, rank reversals may occur in the SAR where the ![]() s are normalised. Rank reversal arguments, often done in the context of the AHP, have not seriously raised questions about the validity of the SAR. Often, the normalisation of alternative priorities has been mentioned as possible reasons for it (see [1] and [2] ). Thus, keeping the SAR as the unquestioned aggregation rule, attempts are made [11] to find solutions for the rank reversal problem by adding ambiguity to criteria weights. New versions of the AHP called “referenced AHP” and “B-G modified AHP” were introduced. Examples used in [11] required additional information about the absolute preference scores of the alternatives (note variables Ti,k and other related derived ones in [11] ). But no further discussions were presented to indicate how computations can be done when such additional information would not be available as it is the case commonly encountered in the AHP.
s are normalised. Rank reversal arguments, often done in the context of the AHP, have not seriously raised questions about the validity of the SAR. Often, the normalisation of alternative priorities has been mentioned as possible reasons for it (see [1] and [2] ). Thus, keeping the SAR as the unquestioned aggregation rule, attempts are made [11] to find solutions for the rank reversal problem by adding ambiguity to criteria weights. New versions of the AHP called “referenced AHP” and “B-G modified AHP” were introduced. Examples used in [11] required additional information about the absolute preference scores of the alternatives (note variables Ti,k and other related derived ones in [11] ). But no further discussions were presented to indicate how computations can be done when such additional information would not be available as it is the case commonly encountered in the AHP.
Here, in this research, we may be tempted to redefine the criteria weights as follows absorbing the norms (i.e., additional information) of the priority vectors:
![]() (18)
(18)
But, because of the recursion relations in Equation (14) and Equation (16), the new weights![]() , which depend on the number of alternatives n, may change if a new alternative is added or an existing one is deleted. Thus,
, which depend on the number of alternatives n, may change if a new alternative is added or an existing one is deleted. Thus, ![]() can be called an adjusted weight. Choo, Schoner and Wedley [12] analysed the interpretation of criteria weights referring to several multi-criteria decision-making models (e.g., Linking pin AHP, Referenced AHP, Saaty’s AHP, Interactive MCDM, MVT SMART, Outranking Electre). They concluded that the most common interpretation of criteria weights was: marginal contribution, trade-offs, gradient of utility function, scaling factor and criteria importance. Here, in this research, criteria weights wp represent the importance of criteria as well and they get adjusted by the norms of priority vectors creating the adjusted weights
can be called an adjusted weight. Choo, Schoner and Wedley [12] analysed the interpretation of criteria weights referring to several multi-criteria decision-making models (e.g., Linking pin AHP, Referenced AHP, Saaty’s AHP, Interactive MCDM, MVT SMART, Outranking Electre). They concluded that the most common interpretation of criteria weights was: marginal contribution, trade-offs, gradient of utility function, scaling factor and criteria importance. Here, in this research, criteria weights wp represent the importance of criteria as well and they get adjusted by the norms of priority vectors creating the adjusted weights![]() . wp is obtained from a DM’s inputs and
. wp is obtained from a DM’s inputs and ![]() is a derived quantity. They appear in formulations as we propose that aggregation should be done using the modified rule MAR as the correct one and we derived it from a general mathematical approach independent of any particular MCDA tool or method.
is a derived quantity. They appear in formulations as we propose that aggregation should be done using the modified rule MAR as the correct one and we derived it from a general mathematical approach independent of any particular MCDA tool or method.
3. Using the Proposed Aggregation Rule: Special Case of the AHP
In the AHP, we can determine weights wp and the local normalised alternative priorities ![]() (
(![]() ) for each criteria p (p =1,.., m) through pairwise comparisons and possibly by the eigenvalue method. However, how do we compute
) for each criteria p (p =1,.., m) through pairwise comparisons and possibly by the eigenvalue method. However, how do we compute![]() ? Zahir [7] discussed this and presented a computational algorithm suggesting the need for extra inputs of m estimates for
? Zahir [7] discussed this and presented a computational algorithm suggesting the need for extra inputs of m estimates for ![]() (n = 1 and
(n = 1 and![]() ) and the use of the recursion relations of Equation (14). Alternatively, a) one can estimate m values for
) and the use of the recursion relations of Equation (14). Alternatively, a) one can estimate m values for ![]() for any particular value of n, assuming a stochastic distribution or b) one can make a direct estimate for the norms along with errors. Then, one can compute an overall error estimate for aggregate normalised priorities. In cases a) and b), once a set of values are chosen for
for any particular value of n, assuming a stochastic distribution or b) one can make a direct estimate for the norms along with errors. Then, one can compute an overall error estimate for aggregate normalised priorities. In cases a) and b), once a set of values are chosen for ![]() s, their successive values (i.e., for addition or deletion of an alternative) are restricted by the recursion relations given in Equation (14) and Equation (16). These equations manifest reasoning that links the decision spaces in the cognitive space of the decision problem (see Section 5 below for more).
s, their successive values (i.e., for addition or deletion of an alternative) are restricted by the recursion relations given in Equation (14) and Equation (16). These equations manifest reasoning that links the decision spaces in the cognitive space of the decision problem (see Section 5 below for more).
In the following formulations, we will assume that there are n alternatives, so we will suppress the index n and will restore it only in the final results. Estimating values for ![]() directly as in a) and b) above may be involved. However, in a fully consistent case, the recursion relation of Equation (14) can be used conveniently to get values for
directly as in a) and b) above may be involved. However, in a fully consistent case, the recursion relation of Equation (14) can be used conveniently to get values for ![]() for any n starting from n = 1 when we have only one alternative. The preference score of one alternative is the same as the norm of the priority vector in this case. The normalised criteria weights and the normalised relative priorities for alternatives can be obtained from eigenvalue equations from pairwise comparison matrices. The recursion relation will generate successive estimates for the norms and thus facilitate aggregation based on the MAR. We describe the procedure in an algorithmic form in Text Box 1 (see [7] ) for an earlier version) and demonstrate it step by step using a numerical example in Appendix B.
for any n starting from n = 1 when we have only one alternative. The preference score of one alternative is the same as the norm of the priority vector in this case. The normalised criteria weights and the normalised relative priorities for alternatives can be obtained from eigenvalue equations from pairwise comparison matrices. The recursion relation will generate successive estimates for the norms and thus facilitate aggregation based on the MAR. We describe the procedure in an algorithmic form in Text Box 1 (see [7] ) for an earlier version) and demonstrate it step by step using a numerical example in Appendix B.
![]()
In Step 3.1 of Text Box 1, m estimates for the preference scores for alternative 1 is required. In MAVT, such values are obtained from value functions. However, m estimates for the preference scores for alternative 1can be estimated assuming a Beta distribution as a possible choice if we want to deal with the underlying uncertainty stochastically.
Let a decision maker estimates the norm (n = 1), following a Beta distribution, as follows:
bp = high end estimate for![]() , ap = low end estimate for
, ap = low end estimate for![]() , mp = most likely estimate for
, mp = most likely estimate for ![]()
Then, then ![]() can represent the average value for the preference score as computed by using well-known formula
can represent the average value for the preference score as computed by using well-known formula
Average score for![]() , and variance
, and variance ![]()
Zahir [7] also suggested a technology-based visual interface for estimating the preference scores ![]() in a comparative mode in reference to m criteria. Such visual interfaces have been used in some AHP software (e.g., VISAÔ-a software package not currently available, MCDSS [13] .
in a comparative mode in reference to m criteria. Such visual interfaces have been used in some AHP software (e.g., VISAÔ-a software package not currently available, MCDSS [13] .
4. Discussion of Results and Future Research
In the preceding sections, we observed that as we move from one decision space to another (obtained by adding or deleting an alternative), the decision model can generate meaningful results only if the aggregation rule is the correct one. This “correctness” is based on our reasoning, i.e., ranks should not reverse when they are not expected to. We illustrated with numerical examples how the MAR supported our correct expectations. Deficiencies of the SAR were detected only when logical reasoning could not be satisfied by calculated results as an alternative was added to or deleted from a decision model. This observation emphasises the need for testing the validity of analytic modelling over an expanded model space. In the AHP (or MAVT using the SAR), if the early developers considered results of two decision spaces (obtained by adding and subtracting alternatives), they would have identified the deficiency of the SAR. An improved aggregation rule that incorporated the unit of scale would have been used in the normalisation of alternatives such as the MAR being discussed in this paper. Such an expanded “big picture” framework is outlined below.
4.1. Cognitive Space and Decision Space: Framework for Avoiding Modelling Deficiencies
As more alternatives (or criteria) are added or some are deleted, the decision space expands or contracts creating a new decision space for the underlying decision model. The set of related decision spaces collectively is the cognitive space of the decision problem, and we try to link them through reasoning and understanding. Each decision space is also a cognitive sub-space where model formulations are defined in terms of logic, reasoning and facts. Often, the links among decision spaces are done in human minds and are left out of the decision models and thus each model is treated independently in its own decision space. But, together they are discussed by researchers in their cognitive domain via reasoning processes. Our memory is a repository of information and it plays a significant role in linking the analyses of the decision spaces via reasoning. Thus, it helps us connect scenarios in decision spaces logically to the satisfaction of our rational minds.
We can think of a Gedanken experiment in reference to the example in Section 4. We keep the inputs same as in Section 4. Suppose a DM computes the relative priorities using the SAR for three alternatives. And then she takes a nap and wakes up when she has no memory of the priorities derived before the nap. Now, she computes the relative priorities using the SAR again for four alternatives and obtains new results. Since she has no memory of the results she obtained before the nap, does it matter even if the ranks now are reversed? Most probably it does not. However, in reality we have memory, and our cognitive process finds reasoning to link findings and results from related decision spaces. The links of reasoning connecting the results from one decision space to another as they reside in our memory are not incorporated in the decision models or, may be, models are deficient in part. We reason in our minds. Sometimes, we also fail to satisfy our reasoning and then we raise the question about the validity of a decision model as it stands. It may be due to a flaw in parts of the model and therefore it needs to be corrected. Another approach that has not been widely pursued in practice may be to extend the decision model across the cognitive space that would also model the reasoning links among the decision spaces. That would also help us find a solution to an apparent imperfection in a decision model.
As it has been discussed earlier, when a new alternative is added or an existing alternative is deleted (i.e., moving from one decision space to another in the cognitive space of the decision problem (see Figure 3) by expanding or contracting the decision space), the ranks may be reversed in the SAR-based AHP. We face a problem in our reasoning as we find it difficult to understand the reversal of ranks when such a reversal of ranks is not supposed to happen. In the MAR, associated recursion rules demonstrate how the units of scale (set by the norm of the preference vectors) change as we make a transition from one decision space to another (i.e., from DS-i to DS-j in Figure 3). The MAR takes this effect into the formulation and thus preserves ranks of existing alternatives when they are expected to preserve. The MAR models decision spaces DS-i and DS-j and also represents cognitive link CLij representing the reasoning that links DS-i and DS-j in the cognitive space. CLij represents the recursion rules that asserts that norms (setting the scale of normalisation) of priority vectors change as an alternative is added or deleted, and the MAR incorporates this assertion preserving ranks when it should. The SAR is deficient as it does not incorporate the scale of normalisation and hence produces unwanted rank reversals.
![]()
Figure 3. Decision spaces in cognitive space.
concept of a scenario is still an evolving one but it is clear that each scenario has a context. Tversky and Kahnemann [18] realised difficulties in developing scenarios and stated “it is exceedingly difficult for the human mind to apprehend sequences of variations of several interacting factors. We suggest that in evaluating the probability of complex events, only the simplest and most likely scenarios are likely to be considered.” In this paper, we keep our discussions about scenarios limited to the MCDA.
Parameter values change.
New parameters enter.
Old parameters may drop out.
Expressions are re-evaluated (e.g., the recursion relations in preceding sections).
New constraints may emerge.
And so on.
4.2. Future Research
While we discussed the multi-criteria decision problem in light decision spaces, we can extend the concept to scenarios applicable to other areas of decision sciences. In management science and operational research, we make models for inventory/supply chain, resource allocation, financial market analysis, portfolio management, etc. based on a particular scenario (analogous to a decision space). Then, we change models as scenarios change (often probabilities are assigned to each scenario in scenario analysis). We try to understand the varying results in our reasoning as we connect scenarios utilising our memory and cognitive strength. It may be possible to include intra-scenario reasoning by having cognitive links in the models spanning more than one scenario. If the models cannot explain results from two scenarios, that can be attributed to a deficient component or weakness of the model itself and thus will call for improvement in the model. We can also try to understand the significance of such integrated multi-scenario decision modelling in light of system thinking [20] . An inter-related reasoning embedded in the expanded analytics is expected to help understand “the whole” for better decision making. The multiple decision spaces or scenarios will be linked by a network in the cognitive space with an objective to assist in forming a decision representing a “big picture”.
5. Conclusion
We identified the deficiency of the traditional weighted sum aggregation rule used in the AHP and possibly in the MAVT with the prior normalisation as the cause for rank reversals and proposed a modified aggregation rule as a remedy. Utilising recursion rules, we analyzed the additive aggregation process in light of the new aggregation rule. We also suggested ways how it could be used with the AHP or MAVT with prior local normalisation. The ideas are illustrated with numerical examples. Also, we discussed possibilities for extending usual modelling techniques developed in the context of a particular decision space or scenario to an expanded form in the cognitive space. Concepts of satisficing and bounded rationality were invoked for managing such expansions. Testing the validity of mathematical models in decision sciences, operations management and possibly economics may need the support of a “big picture” beyond a single scenario.
Appendix A
The aggregation rule that we derived in the text (also see [7] ) preserves rank of any two alternatives when a new alternative is added or an existing one is deleted. This is independent of the model used to derive normalised local priorities of alternatives under each criterion. We give the mathematical proof below following previous work [7] .
1) An alternative is added
Let ![]() and
and ![]() be the aggregate relative priorities of two alternatives in the decision space having n alternatives and m criteria
be the aggregate relative priorities of two alternatives in the decision space having n alternatives and m criteria ![]() and
and ![]() be the same after we add another alternative (i.e., (n+1) alternatives in the decision space). From Equation (11) we have,
be the same after we add another alternative (i.e., (n+1) alternatives in the decision space). From Equation (11) we have,
![]() (A1)
(A1)
From Equation (14), we have
![]() (A2)
(A2)
However, in a fully consistent case, we have from Equation (5) and Equation (14),
![]() (A3)
(A3)
So, finally we get from Equation (A2),
![]() (A4)
(A4)
2) An existing alternative is deleted
Let ![]() and
and ![]() be the aggregate relative priorities of two alternatives in the decision space having n alternatives and m criteria
be the aggregate relative priorities of two alternatives in the decision space having n alternatives and m criteria ![]() and
and ![]() be the same after we delete an existing alternative (i.e., (n − 1) alterna- tives in the decision space). From Equation (11) we have,
be the same after we delete an existing alternative (i.e., (n − 1) alterna- tives in the decision space). From Equation (11) we have,
![]() (A5)
(A5)
From Equation (15) and Equation (A5), we have
![]() (A6)
(A6)
However, in a fully consistent case, we have from eqs (5) and Equation (15),
![]() (A7)
(A7)
So, finally we get from Equation (A6),
![]() (A8)
(A8)
Appendix B
A Numerical Example for Using the MAR
For the sake of illustration, in this section we demonstrate the use of the algorithm given in Section 3 for computing aggregate relative priorities in the AHP using a numerical example. It is a two-level hierarchy having three criteria and three alternatives. It is the same example as the one employed in [21] . Below it is presented in a tabular form. It is the same example as the one employed in [21] and is presented below in Table 1.
![]()
Table 1. Preference scores for three alternatives with three criteria.
With absolute scores known, we can construct pairwise comparison matrices under each criterion and compute normalised local relative priorities as in Table 2 (since we have the absolute scores, the relative priorities could be computed directly as well).
![]()
Table 2. Normalised relative priorities.
Aggregate relative priorities using the SAR and the MAR (Equation (12) and Equation (11) respectively) are given in Table 3.
![]()
Table 3. Aggregate relative priorities using the SAR and the MAR.
In Table 3, numbers in the SAR and the MAR columns are not the same as noted earlier. In the AHP, norms are not known and thus using the MAR is problematic. Algorithm of Text Box 1 utilizes additional information needed as shown in the shaded block in Table 1. The minimum set of information required is shown in the shaded block of Table 4,
![]()
Table 4. Initial inputs needed to implement the algorithm in Text Box 1.
We add another alternative and the PCMs are given in Table 5.
![]()
Table 5. Pairwise comparison matrices for two alternatives.
The normalised relative priorities obtained from the PCMs using the eigenvalue method are calculated in Table 6.
![]()
Table 6. Local relative priorities obtained from PCMs in Table 5 and using eigenvalue method.
Using the norms in the bottom row of Table 4 and the recursion relation Equation (14), we get new norms in Table 7.
![]()
Table 7. Calculated norms for two-alternative priority vectors using the recursion relation.
Next we add a third alternative and the PCMs are given in Table 8.
![]()
Table 8. Pairwise comparison matrices for three alternatives.
The normalised local relative priorities derived from the PCMs using the eigenvalue method are presented below in Table 9.
![]()
Table 9. Local normalised relative priorities obtained from PCMs in Table 8 and using eigenvalue method.
Using the numbers in Table 7, Table 9 and the recursion relation of Equation (14), we have the new norms for three alternatives in Table 10.
![]()
Table 10. Norms for three-alternative priority vectors using the recursion relation.
Finally, the aggregate relative priorities computed using the MAR are (compare with Table 3) given in Table 11.
![]()
Table 11. Aggregate relative priorities using the MAR.
The above numerical exercise demonstrates how the MAR can be used in the AHP as explained in the algorithm of Text Box 1. We performed extensive numerical analysis and confirmed that the final results are independent of the relative order of the alternatives. Rank reversals are avoided using the MAR as long as the comparisons are consistent. In the presence of inconsistency, rank reversal can happen even with the MAR; but that is acceptable as imperfections in judgments. We performed simulation of the algorithm with random presence of inconsistencies and observed rank reversals varying with amount of inconsistencies (see [22] for details). If we
have a simple hierarchy with one level of m criteria and n alternatives, we need m additional inputs for![]() . We need
. We need ![]() pairwise comparisons for the criteria and
pairwise comparisons for the criteria and ![]() pairwise comparisons for alternatives. In relative term, this fraction Q of additional information is,
pairwise comparisons for alternatives. In relative term, this fraction Q of additional information is,
![]() ; for m = 5 and n = 5, Q is only 9%.
; for m = 5 and n = 5, Q is only 9%.
However, the procedure involves extra computational steps but generates correct aggregate relative priorities for the alternatives. To substantiate this claim, let us add another alternative (D) to the example above. The PCMs are given in Table 12.
![]()
Table 12. Pairwise comparison matrices for four alternatives.
The normalised relative priorities obtained by eigenvalue method are calculated in Table 13.
![]()
Table 13. Local normalised relative priorities obtained from PCMs in Table 12 and using eigenvalue method.
Using the numbers in Table 10 and Table 13 and the recursion relation Equation (14), we present the computed norms for three alternatives Table 14.
![]()
Table 14. Norms for four alternative priority vectors using the recursion relation.
The aggregate relative priorities are (using both the MAR and the SAR) presented in Table 15.
![]()
Table 15. Aggregate relative priorities using the MAR and the SAR.
The important point to note is that the ranks of A and B are reversed by the SAR but are preserved by the MAR! Therefore, if we use the MAR that was derived in Section 3, we can avoid the rank reversal controversy not only of the AHP but also other additive MCDM s.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/