Newtonian Computation of Perihelion Precession of Mercury—An Update ()

Subject Areas: Classical Mechanics
1. Introduction
Recently [1] [2] we have made two successive numerical computations within the framework of Newton’s laws of the rate of perihelion precession of Mercury which seem to suggest that the actual value of this rate may be somewhat higher than the currently accepted value of 532 arc sec/cy. We have also pointed out that an important reason for introducing error into the method of computations is the ability of the double precision computing systems to handle numbers only up to about sixteen decimal digits in accuracy. All methods of numerical integrations of the differential equations of motion of the planetary system including even the simplest Euler’s algorithm are to a certain degree or other affected by this limitation insofar that such methods neglect the planetary contributions while retaining the corresponding solar ones. To illustrate this point more clearly let us for example consider the Euler’s algorithm in Ref. [2] (see Equation 2(a) and 2(b))
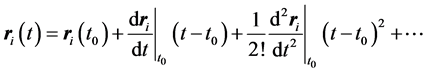 (1)
(1)
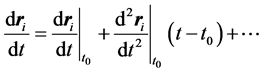 (2)
(2)
where the time step of integration is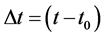 . In Section 2 below we will present results of computations when
. In Section 2 below we will present results of computations when 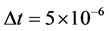 day. However for the moment let us see what effect such a value of the time step will have
day. However for the moment let us see what effect such a value of the time step will have
on the computation of the terms 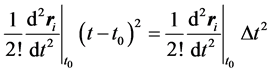 above. An estimate of the magnitude of
above. An estimate of the magnitude of 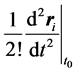 in the case of Mercury due to solar attraction is 108 meters/day2. If this is multiplied by
in the case of Mercury due to solar attraction is 108 meters/day2. If this is multiplied by 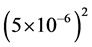
day2 we obtain a quantity which can be added to  (which has a magnitude roughly about
(which has a magnitude roughly about 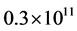 meters) in a double precision computing system for each single time step of integration. However the planetary
meters) in a double precision computing system for each single time step of integration. However the planetary
contribution to 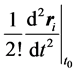 which is
which is 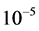 to
to  (for Jupiter to Earth + Moon respectively) times of that of
(for Jupiter to Earth + Moon respectively) times of that of
the solar contribution is entirely lost. Thus this is a neglect of a corresponding planetary contribution to some solar one and hence it will show a lower value of the perihelion precession in the final result as planets are solely responsible for Mercury’s perihelion advance in the Newtonian theory. We have noted in our previous paper (Ref. [2] ) that the Euler’s method is possibly the best amongst all methods to account for these planetary effects as the major contribution in Equation (1) and (2) above come from the terms linear in 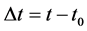 and if
and if 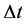 does not fall below
does not fall below  day this will be reflected well in the final result. In Section 3 we discuss a modified
day this will be reflected well in the final result. In Section 3 we discuss a modified
Euler algorithm which neglects the term 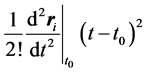 in Equation (1) which while introducing some error
in Equation (1) which while introducing some error
in the position coordinates for a particular value of  as compared with the Euler algorithm will give a more correct estimate of the perihelion advance rate within limitations of machine precision.
as compared with the Euler algorithm will give a more correct estimate of the perihelion advance rate within limitations of machine precision.
2. Computations of the Perihelion Advance Rate with ![]() Day
Day
In our previous paper [2] we have produced a table giving the calculated values of the perihelion advance per century for four different values of the time step. A method of obtaining the various values of the perihelion ad- vance per century corresponding to any arbitrary time step from these four values has been discussed there (see Equation (3) of this reference). In terms of the quantities![]() ,
, ![]() ,
, ![]() and
and ![]() in Equation (3) of Ref. [2] (which can be obtained from the four different values of the perihelion advance per century corresponding to four dif- ferent time steps) we express the perihelion advance per century x in terms of any arbitrary time step
in Equation (3) of Ref. [2] (which can be obtained from the four different values of the perihelion advance per century corresponding to four dif- ferent time steps) we express the perihelion advance per century x in terms of any arbitrary time step ![]() as
as
![]() (3)
(3)
From the previously determined values of![]() ,
, ![]() ,
, ![]() and
and ![]() we get for
we get for ![]() day the value of x to be 535.1 arc sec/cy. A direct computation of the perihelion advance by solving the equation of motion using Euler’s algorithm for this value of
day the value of x to be 535.1 arc sec/cy. A direct computation of the perihelion advance by solving the equation of motion using Euler’s algorithm for this value of ![]() is shown below in Figure 1 for the exactly same period as was done in Figure 1 of reference [2] . The Matlab data statistics calculator gave a mean value of perihelion advance to be 534.1 arc sec/cy. This difference between 535.1 and 534.1 arc sec/cy may be due to the fact that we have reached the limiting value of
is shown below in Figure 1 for the exactly same period as was done in Figure 1 of reference [2] . The Matlab data statistics calculator gave a mean value of perihelion advance to be 534.1 arc sec/cy. This difference between 535.1 and 534.1 arc sec/cy may be due to the fact that we have reached the limiting value of ![]() for our double precision computing system as explained in the previous section. Only a computation in a quadruple precision machine using the modified Euler algorithm can give a more accurate value of the quantity we are trying to calculate. Moreover we remind the reader that these small values of
for our double precision computing system as explained in the previous section. Only a computation in a quadruple precision machine using the modified Euler algorithm can give a more accurate value of the quantity we are trying to calculate. Moreover we remind the reader that these small values of ![]() require exceedingly large computer time so other more efficient algorithms like Adams or Adams Bashforth may be tried first in the quadruple precision system.
require exceedingly large computer time so other more efficient algorithms like Adams or Adams Bashforth may be tried first in the quadruple precision system.
3. The Modified Euler Algorithm
At the present moment the author does not have access to quadruple precision computing systems equipped with ODE solvers and so in order to make the best use of the available facilities we tried to apply a modified form of the Euler algorithm that is a modified form of Equations (1) and (2). These are
![]()
Figure 1. The advance of the longitude of perihelion of Mercury as obtained from a numerical solution of the coupled system of N (actually N − 1 of the type of Equation (1) of Ref. [2] ) ordinary differential equations. The initial time is JJ = 2451600.5 and the total period of computation is 220 years. The plot is that for a period of about the last 30 years. The value of time step = 5 × 10−6 day and the method of integration is the Euler algorithm.
![]() (4)
(4)
![]() (5)
(5)
and are identified as the “Euler algorithm” in certain textbooks instead of Equations (1) and (2). Although this neglect of the term proportional to ![]() will degrade the solution to a certain extent the value of the precession rate may be closer to the actual rate if it is calculated using this algorithm considering the reasons given in Section 1 above. The calculations were done for
will degrade the solution to a certain extent the value of the precession rate may be closer to the actual rate if it is calculated using this algorithm considering the reasons given in Section 1 above. The calculations were done for ![]() day time step and the perihelion advance is shown in Figure 2. The average perihelion advance rate as given by Matlab data statistics calculator is 546 arc sec/cy. This is substantially higher than the 538 arc sec/cy which is obtained using the normal Euler algorithm that is Equations (1) and (2). Thus without claiming that the Newtonian precession rate is indeed much higher than 532 arc sec/cy (the value predicted by perturbation calculations from the end of the 19th century) we just make a sober assessment that there is an urgent need to calculate the perihelion precession rate of Mercury using more sophisticated techniques. The actual value may well exceed 540 arc sec/cy.
day time step and the perihelion advance is shown in Figure 2. The average perihelion advance rate as given by Matlab data statistics calculator is 546 arc sec/cy. This is substantially higher than the 538 arc sec/cy which is obtained using the normal Euler algorithm that is Equations (1) and (2). Thus without claiming that the Newtonian precession rate is indeed much higher than 532 arc sec/cy (the value predicted by perturbation calculations from the end of the 19th century) we just make a sober assessment that there is an urgent need to calculate the perihelion precession rate of Mercury using more sophisticated techniques. The actual value may well exceed 540 arc sec/cy.
4. In Place of a Conclusion an Answer to the Constructive Comments of the Referee
First of all I would like to thank the anonymous referee for his constructive criticism. In his report he has referred to this link http://www.math.toronto.edu/~colliand/426_03/Papers03/C_Pollock.pdf from which I quote the following: “It is possible to model, very precisely, the Newtonian force each planet was expected to exert on Mercury. An elegant approximation, however, was described by Price and Rush in their paper entitled Non-relativistic contribution to Mercury’s perihelion precession. They replaced each of the outer planets by a ring of uniform linear mass density. Since Mercury’s precession is slow compared with the ortits of even Uranus, their approach yields a fairly accurate time-averaged effect of the moving planets’ effects. An sketch of their calculations follows. First, let’s replace each planet by a ring with linear mass density given by the following
![]()
Figure 2. The same computation as in Figure 1. using the modified Euler algorithm with time step = 2 × 10−5 day. The plot is for a period starting from about the 149th year after the initial time JJ = 2451600.5 and ending at about the 184th year after that same date.
equation:
![]()
where ![]() is the linear mass density along the orbit of the ith planet from the sun, Mi is the mass of the ith planet, and Ri is the radius of the ith planets orbit, which is assumed to be circular.” The present author feels that the ring like mass concept has been more precisely introduced by Stewart [3] where he considers an elliptical ring rather than a circular one. We quote the expression for the potential of this ring
is the linear mass density along the orbit of the ith planet from the sun, Mi is the mass of the ith planet, and Ri is the radius of the ith planets orbit, which is assumed to be circular.” The present author feels that the ring like mass concept has been more precisely introduced by Stewart [3] where he considers an elliptical ring rather than a circular one. We quote the expression for the potential of this ring
![]()
where all notations are explained in figure 1 of this reference. If we take the gradient of this quantity it will be found to be zero at ![]() which means that there is no force on the Sun by any of the perturbing planets. Thus the Sun remains fixed in an inertial frame except perhaps because of the small effect of Mercury. Thus in the heliocentric frame there are no pseudo forces on Mercury because of this inertial approximation. The referee in his report has asked “First at all, the author must state clearly in the paper the way in which the effect of the perturbation of the planets is took into account. Usually, the so-called ring approximation is used (see references above). In this approximation the planets are approximated by a ring of mass along their orbits but, in principle, the real orbit could also be used if the integration time is sufficiently large.” In Equation (1) of our previous papers (that is of the references [1] and [2] ) which we quote here once more
which means that there is no force on the Sun by any of the perturbing planets. Thus the Sun remains fixed in an inertial frame except perhaps because of the small effect of Mercury. Thus in the heliocentric frame there are no pseudo forces on Mercury because of this inertial approximation. The referee in his report has asked “First at all, the author must state clearly in the paper the way in which the effect of the perturbation of the planets is took into account. Usually, the so-called ring approximation is used (see references above). In this approximation the planets are approximated by a ring of mass along their orbits but, in principle, the real orbit could also be used if the integration time is sufficiently large.” In Equation (1) of our previous papers (that is of the references [1] and [2] ) which we quote here once more
![]()
shows that all the perturbing terms including the pseudo force terms are present in the summation. Numerical integration does not necessitate any ring like assumption as each of the terms above is integrated as it is by the integration algorithm. The only error that is introduced is by the use of finite quantities instead of infinitesimals. These errors are larger for the simple algorithms like the one used here necessitating smaller time steps. Of a different nature is the error introduced by machine precision which affects all algorithms although to varying extents as we noted earlier. It is difficult to quantify the extent of the error for any given algorithm. The referee has raised an issue which is quoted as “Another problem comes from the integration method. Finite precision methods introduce a perturbation by themselves and this gives rise to an extra precession of the perihelion (this is a general consequence of Bertrand’s theorem).” to which I should say that finite precision is a property of the computing system or the language and is dependent on the machine architecture for example the normal Matlab is double precision. By the phrase “finite precision method” (of integration?), I feel a certain amount of confusion is being introduced as it is not clear what is being referred to that is to the algorithm or to Matlab. Now the question as to whether such computations are overestimating the rate of perihelion advance is difficult to answer (it may well be underestimating). I would just like to state that if Prof. M.G. Stewart’s calculations are correct then perturbation theory should predict no more than 529 arc sec/cy as the node of Mercury precess at a rate of
−451 arc sec/cy and a term ![]() must be added to the value obtained by Stewart if we stick to the
must be added to the value obtained by Stewart if we stick to the
definition of longitude of perihelion as is used for example by Clemence. All these have been explained in one of our previous papers that is Ref. [1] . Lastly the referee has raised a connection of the present topic with that of general relativity. At the present moment I feel that this will create more confusion and divert the attention from the problem at hand. I would request the referee to leave this to posterity.