Particle Physics Can Be Investigated from a Thermodynamic Point of View ()
Subject Areas: Particle Physics, Thermodynamics

1. Introduction
Through generalizing in some interdisciplinary areas [1] [2] , thermodynamics has successfully led to a series of new concepts, such as quantum heat engine (employing as working agents multi-level systems instead of gas-filled cylinders) [3] [4] , information entropy (an equivalence between information and entropy is postulated) [5] and quantum entanglement (in some way analogous to thermodynamic energy) [6] [7] . These concepts imposing the thermodynamic aspects of microscopic objects of interest, inspire us to study particle physics from a thermodynamic standpoint, and make us believe that a single particle could also exhibit its thermodynamic properties since it carries an intrinsic spin, spreads like a wave and acts as a complicated system. In this paper, we will give the basic elements of our analogy between particle physics and thermodynamics. To provide background for the details of the analogy, we propose the particle thermodynamic laws, and further develop the operational definitions of particle state functions to discuss the thermodynamic properties of particle objects.
2. Analogy between Particle Object and Thermodynamic System
To develop the full analogy between particle object and thermodynamic system, we need to recall that particle decay is exactly representing a kind of spontaneous process, just as heat passing from a higher to a lower temperature (the situation is shown as Table 1). So, we take notice of the thermodynamic meaning of particle object
with moving velocity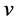 , and treat its relativistic energy
, and treat its relativistic energy 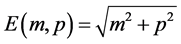 (nature units:
(nature units: 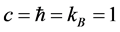 adopted) as the enthalpy function
adopted) as the enthalpy function
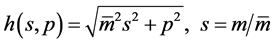 (1)
(1)
of which the differential reads
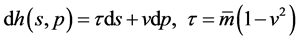 (2)
(2)
here 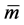 denotes the mean value of mass
denotes the mean value of mass 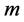 with a distribution width
with a distribution width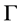 ,
, 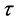 is the intrinsic temperature of particle object, and
is the intrinsic temperature of particle object, and 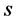 is the intrinsic entropy with a quantized mean value of
is the intrinsic entropy with a quantized mean value of 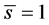 (here called entron, i.e. quantum of entropy). Therefore, following from the above form, there also exist other functions in which one or more variables is replaced by its slope, the functions with the same information content can be obtained by applying the following transform. For example, a function defined by
(here called entron, i.e. quantum of entropy). Therefore, following from the above form, there also exist other functions in which one or more variables is replaced by its slope, the functions with the same information content can be obtained by applying the following transform. For example, a function defined by
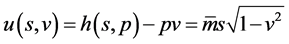 (3)
(3)
it yields the transition from independent variables 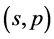 to
to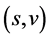 , and then gives
, and then gives
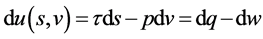 (4)
(4)
The differential above suggests that 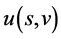 may be treated as the internal energy of moving particle with the natural variables
may be treated as the internal energy of moving particle with the natural variables ![]() (identified with entropy) and
(identified with entropy) and ![]() (analogous to usual volume),
(analogous to usual volume), ![]() is the bound or disorder energy (analogous to heat), and
is the bound or disorder energy (analogous to heat), and ![]() is the useful energy (analogous to work). Importantly, such analogy can help us to find an interesting connection with Carnot theory, and then explore PCE that works in speed space only when decay occurs. In working process, PCE exchanges energy with its surrounding fields (a special kind of heat reservoirs [8] [9] ) through field theory mechanism [10] [11] .
is the useful energy (analogous to work). Importantly, such analogy can help us to find an interesting connection with Carnot theory, and then explore PCE that works in speed space only when decay occurs. In working process, PCE exchanges energy with its surrounding fields (a special kind of heat reservoirs [8] [9] ) through field theory mechanism [10] [11] .
Now, let us imagine there is a particle ![]() of mass
of mass ![]() decaying into
decaying into ![]() of
of![]() :
:![]() , of which the
, of which the ![]() field can be treated as the working substance to be taken around the cycle. The surroundings consist of constant temperature heat reservoirs, one (the field used to excite
field can be treated as the working substance to be taken around the cycle. The surroundings consist of constant temperature heat reservoirs, one (the field used to excite![]() ) at
) at ![]() and the other (the
and the other (the ![]() field) at
field) at
![]() . The
. The ![]() field system and surroundings make up a PCE. It operates reversibly between
field system and surroundings make up a PCE. It operates reversibly between
the two heat reservoirs, with, in each cycle (called particle Carnot cycle), heat ![]() entering at
entering at![]() ,
, ![]() leaving at
leaving at ![]() and useful energy
and useful energy ![]() being delivered. The Carnot cycle operation can be schemed by four steps (see Figure 1):
being delivered. The Carnot cycle operation can be schemed by four steps (see Figure 1):
(i) Isothermal expansion of ![]() field from 1 to 2 at
field from 1 to 2 at![]() , with heat
, with heat ![]() absorbed and a particle
absorbed and a particle ![]() excited.
excited.
(ii) Emerging of ![]() and subsequent adiabatic evolution from 2 to 3.
and subsequent adiabatic evolution from 2 to 3.
(iii) Isothermal compression of ![]() field from 3 to 4 through thermal contact with the entropy sink of
field from 3 to 4 through thermal contact with the entropy sink of ![]()
field at![]() , releasing
, releasing ![]() and delivering
and delivering![]() . It requires
. It requires![]() , i.e.
, i.e.![]() .
.
(iv) Breaking of thermal contact and continuance of adiabatic compression of ![]() field at vacuum state from 4 to 1.
field at vacuum state from 4 to 1.
In the way, PCE is made up, and all PCEs operating between the same two reservoirs have the same efficiency of converting bound energy to useful form, that is
![]() (5)
(5)
![]()
Figure 1. Temperature-entropy diagram for particle Carnot cycle. In working process of the imagined PCE, the distribution of useful energy is completely determined by Carnot’s theorem.
![]()
Table 1. Natural symmetry suggests that a particle object should exhibit thermodynamic behaviors like a complicated system.
here the adiabatic case of ![]() is used. In turn, when observing on
is used. In turn, when observing on![]() , the particle would be at rest, and
, the particle would be at rest, and
![]() in motion with speed
in motion with speed![]() . So that, the temperatures of the two read respectively
. So that, the temperatures of the two read respectively![]() ,
, ![]() , which give
, which give![]() . It clearly tells us that, because of no useful energy de-
. It clearly tells us that, because of no useful energy de-
livered, the efficiency of presented PCE should be zero, namely
![]() (6)
(6)
Moreover, considering no engine more efficient than PCE, we have![]() , and further
, and further
![]() (7)
(7)
This is referred to as Clausius’ inequality, in which, “=” is allowed only for reversible decay process (i.e.![]() ), and in fact
), and in fact ![]() required by the momentum conservation principle (the situation is shown as Fig-
required by the momentum conservation principle (the situation is shown as Fig-
ure 2). Importantly, inequality (7) can lead directly to the principle of increasing entropy for particle physics: in any decay process, the total entropy of relevant particles increases or remains constant, but cannot decrease. In particular, for ![]() meson decay
meson decay
![]() (8)
(8)
the entropy increase trend can be shown as
![]() (9)
(9)
Thus we say it is the principle that determines the irreversibility of particle decay.
3. Particle Thermodynamic Laws
So far, based on the obtained above, we present the following particle thermodynamic laws.
0th law: Particle objects have well-defined values of some set of state variables, being of two types: to some extensive variables (such as![]() ,
,![]() ), there correspond the conjugate intensive variables (such as
), there correspond the conjugate intensive variables (such as![]() ,
,![]() ). When two particles unite to form a heavier one (nuclear fusion), they undergo no whole changes if and only if the intensive variables of the interacting sub-objects, have the same values.
). When two particles unite to form a heavier one (nuclear fusion), they undergo no whole changes if and only if the intensive variables of the interacting sub-objects, have the same values.
1st law: Energy is conserved for all particle processes. The law claims that the particle perpetual mobile of the first kind is absolutely impossible.
2nd law: Exactly as the usual one [12] , this law has two equivalent statements:
(i) Particle at lower temperature (corresponding to small mass) cannot decay spontaneously into the one at higher temperature (corresponding to a large mass); while the constraints on the system and the state of the rest of the world are left unchanged (analogous to Clausius’).
(ii) It is impossible to find a single particle that produces no effect other than the transformation of its bound energy into an equivalent amount of useful form (analogous to Kelvin’s).
In other word, the particle perpetual mobile of the second kind never occurs. The important point is here that, if allow a particle transform its bound energy directly into the useful form, namely![]() , an added momentum
, an added momentum ![]() is yielded, violating momentum conservation. It is proved that, the deep physics behind entropy increasing must be related to momentum transference, whereas in usual thermodynamics, this is overlooked.
is yielded, violating momentum conservation. It is proved that, the deep physics behind entropy increasing must be related to momentum transference, whereas in usual thermodynamics, this is overlooked.
2.5th law: In any particle process, the total momentum cannot increase, nor decrease, but remains constant. As a supplementary item, such law puts restrictions on which processes may occur, or more particularly which processes can never occur even though they are allowed by the 2nd. For example, the decay process of ![]() is forbidden.
is forbidden.
3rd law: It is impossible to design a procedure that can control particle temperature to zero, namely, the absolute zero of particle is never attainable. This law disallows any decay process with 100% efficiency, even if for photon (with nonzero mass) [13] [14] , no exceptions are made.
4. State Functions
To set up the state functions of a decay particle of mass width![]() , we are allowed to treat it as an open thermodynamic system [15] [16] , and substitute complex mass
, we are allowed to treat it as an open thermodynamic system [15] [16] , and substitute complex mass ![]() for
for![]() . This complex mass with a module of
. This complex mass with a module of
![]() (10)
(10)
can determine a mass distribution in the following form
![]() (11)
(11)
Combing with the decay function of![]() , it gives the composite probability distribution of unstable particle, that is
, it gives the composite probability distribution of unstable particle, that is
![]() (12)
(12)
Such the result can help us to write the adjusted enthalpy function in the form of
![]() (13)
(13)
followed by the internal energy
![]() (14)
(14)
So that, the total differential of the function reads
![]() (15)
(15)
with the identifications:
![]() (16)
(16)
Obviously, ![]() should have the meaning of chemical potential, describing the interaction between particle object and its surroundings [17] [18] ,
should have the meaning of chemical potential, describing the interaction between particle object and its surroundings [17] [18] , ![]() the decay efficiency of unstable particle, which in the case of
the decay efficiency of unstable particle, which in the case of ![]() or
or![]() , tends to zero, i.e.
, tends to zero, i.e.![]() . This actually tells us that, only the particle stable or moving with unit speed, would have a decay efficiency of zero.
. This actually tells us that, only the particle stable or moving with unit speed, would have a decay efficiency of zero.
Note that, the Maxwell relations for particle object are a consequence of the fact that the order of the cross derivatives of ![]() does not matter, namely
does not matter, namely
![]() (17)
(17)
accompanied with the chemical potential ![]() satisfies
satisfies
![]() (18)
(18)
These two are corresponding to the usual forms respectively![]() ,
, ![]() in thermodynamics. Figure 3 does make apparent the general trend of increasing chemical potential with increasing mass [19] . This feature can be explained as that, the particle chemical potential is determined by the field interaction with surroundings, the more massive the unstable particle, the higher temperature and the stronger interaction.
in thermodynamics. Figure 3 does make apparent the general trend of increasing chemical potential with increasing mass [19] . This feature can be explained as that, the particle chemical potential is determined by the field interaction with surroundings, the more massive the unstable particle, the higher temperature and the stronger interaction.
If further, apply Legendre transform to![]() , we can also get the free energy and enthalpy of particle object, those are
, we can also get the free energy and enthalpy of particle object, those are
![]() (19)
(19)
![]() (20)
(20)
including the variation of ![]()
![]() (21)
(21)
The relationship enables us to explore an equilibrium criterion for an individual particle keeping contact with its surrounding bath![]() . It is that, in equilibrium, the total entropy of the particle object and of the bath should be maximized at fixed temperature, specifically
. It is that, in equilibrium, the total entropy of the particle object and of the bath should be maximized at fixed temperature, specifically![]() ,
, ![]() , requiring
, requiring![]() ,
, ![]() ,
, ![]() and
and![]() . For example, the equilibrium between electron and radiation field can be reached at a temperature about
. For example, the equilibrium between electron and radiation field can be reached at a temperature about![]() . Now, we summarize the thermodynamic and particle analogies in Table 2.
. Now, we summarize the thermodynamic and particle analogies in Table 2.
Now, consider a particle state with free energy![]() , and by statistical mechanics [21] we define the partition function
, and by statistical mechanics [21] we define the partition function
![]()
Table 2. The suggested analogies between thermodynamic system (TDS) and particle object (PO).
![]() (22)
(22)
where ![]() denotes the occupation number of particle in phase space. Making the usual assumption that the integral is dominated by the most probable states, we obtain
denotes the occupation number of particle in phase space. Making the usual assumption that the integral is dominated by the most probable states, we obtain![]() , yielding
, yielding
![]() (23)
(23)
Hence, to agree with Eq. (19) identifies
![]() (24)
(24)
This is an analogue of Boltzmann relationship for particle physics, which can be made the basis of a theory of fluctuations about particle object in analogy to that of fluctuations about thermodynamic system. Specifically, the fluctuations in![]() ,
, ![]() and
and ![]() are given by
are given by
![]() (25)
(25)
where ![]() is the isochoric heat capacity,
is the isochoric heat capacity, ![]() the isothermal compressibility. Meanwhile, the relationship can also be used to examine the increasing behavior of particle entropy, and thus the evolution function of total decay entropy of
the isothermal compressibility. Meanwhile, the relationship can also be used to examine the increasing behavior of particle entropy, and thus the evolution function of total decay entropy of ![]() is given by
is given by
![]() (26)
(26)
Note the stable particle condition of ![]() and
and![]() , we have
, we have
![]() (27)
(27)
with a change ratio
![]() (28)
(28)
equal to ![]() as
as ![]() (meaning only
(meaning only ![]() decay at the beginning), and “=” allowed only
decay at the beginning), and “=” allowed only![]() . The result shows once again that: the total decay entropy of relevant particles increases or remains constant, but cannot decrease.
. The result shows once again that: the total decay entropy of relevant particles increases or remains constant, but cannot decrease.
Finally, by the definition of particle temperature, we can further get the following relation
![]() (29)
(29)
with ![]() called the probability density of mass, which is analogous to the usual ideal gas equation
called the probability density of mass, which is analogous to the usual ideal gas equation![]() .
.
5. Summary
Up to now, we have explored a new theory for the description of particle physics. And conceptually different from the conventional standpoint, this theory, by treating particle objects as a kind of thermodynamic system, has led to a number of apparently new results: (i) Particle decay behavior is restricted by Carnot’s theorem; (ii) There exist particle thermodynamic laws analogous to the usual ones. Especially, the momentum conservation principle is introduced to supplement the second law; (iii) Some thermodynamic functions, including an equilibrium criterion, are developed to describe particle states; (iv) Boltzmann relationship for particle physics is obtained. We here emphasize any microscopic particle in nature carries its intrinsic entropy with an absolute value near unit, and the total particle entropy never decreases for any decay process. It is important that we find a new route that can be followed to investigate particle physics in the mathematical framework of thermodynamics.