A Model for the Risk of Microcephaly Induced by the Zika Virus (ZIKV) ()
Received 11 May 2016; accepted 11 July 2016; published 14 July 2016

1. Introduction
Zika virus (ZIKV) is an arbovirosis that belongs to the flavivirus family and is transmitted by Aedes aegypti mosquitoes [1] . The first insight of the ZIKV dates back to 1947 in a monkey at the Zika forest in Uganda [2] . The first cases in humans were reported in 1952 in Eastern Africa. Between the years 1977 and 1978, it was reported an outbreak in Malaysia and Indonesia, that it was attributed to a strong rainy season. Several cases were detected again until the year 2007 in the Yap Island at the Micronesia [3] [4] . The WHO and other health care institutions of the affected countries consider the ZIKV as a public health problem. Besides the breeding places increase due to the climatic change, there exists evidence of perinatal transmission in the French Polynesia. Two cases were reported in December (2013) and February (2014). In the first case, the pregnant woman has presented ZIKV symptoms two days before the delivery, in the second one, the mother and the newborn have showed ZIKV symptoms three and four days after the delivery, respectively [5] . Moreover, evidence of sexual transmission has been reported. There were a couple of cases: the first one in Southeastern Senegal in 2008 and the second one during a ZIKV outbreak in Tahiti (2013) [6] [7] .
As the fourth mechanism of transmission, it has been studied the possibility of transmission through blood transfusions [8] . All these facts together lead to the increase of the susceptible people to this disease.
It is very interesting to analyze the possible perinatal transmission since there is not enough information about the potential consequences that ZIKV may cause in the central nervous system of the fetus or the newborn. Specially, taking into account the complications that other arboviruses may cause by the same way. As example, the Chikungunya produces encephalopathy and hemorrhagic fever, or the Dengue may cause a premature delivery or fetal anomalies [5] .
On the other hand, the WHO and the Brazilian ministry of health have alerted about a possible connection between ZIKV and the congenital microcephaly [4] [9] . The WHO has reported that till November 21, 2015 there were detected 739 cases of microcephaly in 9 states of Brazil [9] . Although it is necessary to have more evidence about this issue, this one has turned out in a severe problem for pregnant women since there is no vaccination against this disease.
Taking into account the importance of these previous reports about of the relation between ZIKV and microcephaly in newborns, it is proposed a mathematical model based on non-linear differential equations to describe the dynamics of the ZIKV transmission, with emphasis in a group of susceptible pregnant women.
2. The Model
It has been introduced a theoretical model based in non-linear ordinary differential equations to describe the dynamics of the population incidence of the infected pregnant women that may present fetal microcephaly induced by the ZIKV virus. The variables of the model are as follows:  average number of susceptible people,
average number of susceptible people, 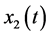 average number of ZIKV infected pregnant women that may induce fetal microcephaly,
average number of ZIKV infected pregnant women that may induce fetal microcephaly, 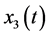 average number of persons infected by ZIKV,
average number of persons infected by ZIKV, 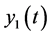 average number of non-carrier mosquitoes,
average number of non-carrier mosquitoes, 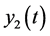 average number of virus-carrier mosquitoes,
average number of virus-carrier mosquitoes,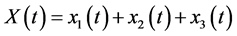 total people population and
total people population and  total population of mosquitoes at time t, respectively. On the other hand, the parameters used for the simulations are: δ: constant flux of susceptible people, μ: the people natural death rate, β: the virus transmission probability from the virus-carrier mosquitoes to the susceptible people, σ: the virus transmission probability from the infected pregnant women to the non-carrier mosquitoes, γ: virus transmission probability from infected people to the non-carrier mosquitoes,
total population of mosquitoes at time t, respectively. On the other hand, the parameters used for the simulations are: δ: constant flux of susceptible people, μ: the people natural death rate, β: the virus transmission probability from the virus-carrier mosquitoes to the susceptible people, σ: the virus transmission probability from the infected pregnant women to the non-carrier mosquitoes, γ: virus transmission probability from infected people to the non-carrier mosquitoes,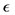 : the adult mosquitoes death rate, θ: the recovery rate of the infected pregnant women, α: the infected people recovery rate, f: the fraction of infected people,
: the adult mosquitoes death rate, θ: the recovery rate of the infected pregnant women, α: the infected people recovery rate, f: the fraction of infected people,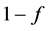 : is the fraction of pregnant women infected by ZIKV.
: is the fraction of pregnant women infected by ZIKV.
The differential equations system of the infectious process is (Figure 1):
 (1)
(1)
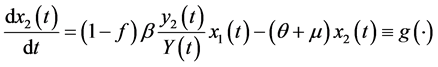 (2)
(2)
 (3)
(3)
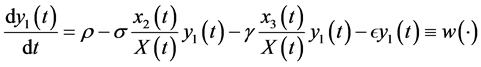 (4)
(4)
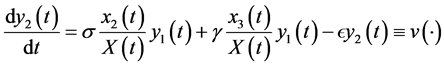 (5)
(5)
where, 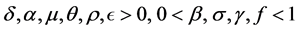 and initial conditions
and initial conditions![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() . By integrating Equations (1)-(5), the system trajectories were obtained:
. By integrating Equations (1)-(5), the system trajectories were obtained:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
These trajectories correspond to the solutions of each population, as shown in the simulations.
3. Stability Analysis
Accounting for an average temperature of around 23˚C, at Armenia (Quindío), we have estimated the transmission probabilities![]() ,
, ![]() and
and![]() ,using the functions reported in [10] [11] .
,using the functions reported in [10] [11] .
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
where,![]() . The parameters
. The parameters ![]() and
and ![]() were estimated considering the Poisson’s process
were estimated considering the Poisson’s process
theory in epidemiology![]() , accounting for a life expectancy in Colombia of 75 years, and an average
, accounting for a life expectancy in Colombia of 75 years, and an average
transmissibility period of 7 days![]() . The parameters values
. The parameters values ![]() and
and ![]() were assigned according to other ones previously reported, as shown in the Table 1.
were assigned according to other ones previously reported, as shown in the Table 1.
The local stability analysis of the model was made by using the data of Table 1. We begin with the calculation of the free of infection and prevalence equilibrium points.
These ones were obtained by solving the following non-linear algebraic system.
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
By applying the MAPLE software, the following equilibrium points were obtained, as seen in Table 2.
To achieve the linearization of the non-linear system 1-5, we have calculated the Jacobianin the generic
equilibrium point![]() ,
,
![]() (19)
(19)
here,
![]()
![]()
With the data of Table 1 and the equilibrium points, the analysis of local stability is realized.
By applying the Jacobian, we obtain the following results.
In Table 2, the local stability analysis of the dynamics system (1 - 5) corresponding to the infected women fraction is summarized. For each equilibrium point are indicated the eigenvalues which describe the stability according to the epidemic threshold (R0).
![]()
Table 2. Local stability analysis of the system for each f.
4. Basic Reproduction Number R0
The epidemic threshold R0 indicates the average number of cases generated by an infected person during the average time of infection in a susceptible population [12] [13] . This one is calculated applying the next generation matrix [13] [14] . To achieve this goal we come back to the dynamic system (1-5) in the following form:
![]() (20)
(20)
From the first three equations of the infectious process, the matrixes were achieved,
![]() (21)
(21)
And the next generation matrix,
![]() (22)
(22)
That it has a characteristic equation with the form,
![]() (23)
(23)
And eigenvalues
![]() (24)
(24)
So then, the spectral radio (dominant eigenvalue) is
![]() (25)
(25)
The local sensitivity is a relative measure of the change in a variable when a parameter changes [15] - [17] . The sensitivity index for R0 is calculated as:
![]() (26)
(26)
where, p is a parameter. From this equation the following indexes are obtained,
![]() (27)
(27)
Table 3 shows the sensitivity values respecting to each parameter. It is possible to see that ![]() is proportional to the infected people recovery rate
is proportional to the infected people recovery rate![]() . Likewise, if the adult death rate increases the
. Likewise, if the adult death rate increases the ![]() decreases, proving that control strategies applied to increase the mosquitoes’ mortality rate help to decrease the ZIKV incidence, and particularly the risk of microcephaly incidence.
decreases, proving that control strategies applied to increase the mosquitoes’ mortality rate help to decrease the ZIKV incidence, and particularly the risk of microcephaly incidence.
5. Simulations and Discussion
The simulations of the system (1 - 5) were performed with the data reported in Table 1 and the MAPLE software. The first graph of Figure 2 shows an almost linear-like behavior of the R0 respecting to the infected people (f) with![]() . The right part of Figure 2 shows the lines of each sensitivity index respecting to each parameter.
. The right part of Figure 2 shows the lines of each sensitivity index respecting to each parameter.
![]()
Table 3. Sensitivity indexes of the R0 as function of each parameter.
In Figure 3, it is observed that if f increase, the pregnant women population achieves a major epidemic peak in the first 10 days. When there is no infection in the pregnant women population the ZIKV virus incidence is around 1700 cases each 10 days. Over 80 days the populations tend to stabilize.
Regarding to the remaining part of the infected population there is a similar behavior with small variations in the epidemic peaks. This population tends to stabilize in values underneath 200 persons in around 40 days.
Finally, Figure 4 shows the trajectories of the infectious process for a small fraction of pregnant women infected by ZIKV. Under the hypothesis of microcephaly induced by ZIKV virus, the proposed model shows the risk of fetal exposition to acquire microcephaly.
![]()
Figure 4. Behavior of populations with f = 0.85.
6. Conclusion
From the analysis of the proposed model, it is observed the effect of the ZIKV acquirement by changing the pregnant women fraction, with the subsequent fetal exposition risk. So, in perspective it is important to model the dynamics including measures to prevent pregnancy as well as control strategies against the vector.
Acknowledgements
AML thanks to Grupo de Modelación Matemática en Epidemiología (GMME), Facultad de Educación, Univ- ersidad del Quindío-Colombia and to the Facultad de Medicina, Benemérita Universidad Autónoma de Puebla- México.