Iterative Method Based on the Truncated Technique for Backward Heat Conduction Problem with Variable Coefficient ()
Subject Areas: Numerical Mathematics, Partial Differential Equation

1. Introduction
In this article, we consider the following backward heat conduction problem (BHCP) with variable coefficient
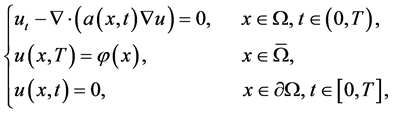 (1)
(1)
where 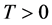 is a positive constant;
is a positive constant; 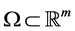 denotes a bounded and connected open domain; the coefficient
denotes a bounded and connected open domain; the coefficient 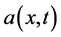 is assumed to be continuous and differentiable with respect to
is assumed to be continuous and differentiable with respect to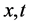 , respectively, and satisfying
, respectively, and satisfying
 (2)
(2)
and
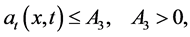 (3)
(3)
our purpose is to determine  for
for 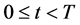 from the final measured data
from the final measured data  which satisfies
which satisfies ; here
; here 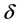 denotes the noisy level.
denotes the noisy level.
This problem is severely ill-posed and the regularization techniques are required to stabilize numerical computations [1] [2] . In past years, many authors have considered the regularization methods for the case  with constant coefficient
with constant coefficient  (see [3] - [6] etc.). For the BHCP with variable coefficients, [7] investigated a case that the coefficient is independent of the time t, i.e.,
(see [3] - [6] etc.). For the BHCP with variable coefficients, [7] investigated a case that the coefficient is independent of the time t, i.e.,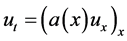 . In 2010, Feng et al. [8] considered problem (1) and proved a condition stability result of Hölder type, then applied a truncated method to regularize it, and the corresponding convergence results have been given. On the other references for BHCP, we can see [9] - [12] , etc.
. In 2010, Feng et al. [8] considered problem (1) and proved a condition stability result of Hölder type, then applied a truncated method to regularize it, and the corresponding convergence results have been given. On the other references for BHCP, we can see [9] - [12] , etc.
Followed the work in [8] , in this paper we use an iterative method to solve problem (1). The idea of this method (see Section 2) mainly comes from the reference [13] , where the authors investigated a backward heat conduction problem (BHCP) with densely defined self-adjoint and positive-definition operator. Recently this method has been used to solve some inverse problems of parabolic partial differential equation (PPDE). For instance, [14] investigated the same problem with [13] by rewriting the solution of inverse problem as the solution of a fixed point equation for an affine operator, and gave the convergence proof by using the functional analysis properties of the linear part of affine operator. Based on the variable relaxation factors, [15] treated the special case  with nonhomogeneous Dirichlet boundary condition and used the boundary element method (BEM) to implement numerical computation.
with nonhomogeneous Dirichlet boundary condition and used the boundary element method (BEM) to implement numerical computation.
Inspired by [13] , in the present paper, we firstly adopt a similar method in [13] to obtain an iterative scheme, then truncate it to get our iterative method (see Section 2); here the data ![]() for
for ![]() will be determined. Under an a-priori and an a-posteriori stopping rule for the iterative step number, the convergence of the algorithm also will be given, and we can see that our convergence results are order optimal as
will be determined. Under an a-priori and an a-posteriori stopping rule for the iterative step number, the convergence of the algorithm also will be given, and we can see that our convergence results are order optimal as ![]() in (1).
in (1).
This paper is constructed as follows. In Section 2, we make a simple review for the ill-posedness of problem (1) and give the description of our iteration method. Section 3 is devoted to the convergence estimates under two stopping rules. Numerical results are shown in Section 4. Some conclusions are given in Section 5.
2. The Ill-Posedness and Description of the Iteration Method
2.1. The Simple Review of the Ill-Posedness for Problem (1)
We make a simple review for the ill-posedness of problem (1) (also see [8] ).
We denote ![]() as the eigenvalues of negative Laplace operator
as the eigenvalues of negative Laplace operator ![]() defined in the space
defined in the space![]() , and satisfy
, and satisfy
![]() (4)
(4)
Further, we suppose that the corresponding eigenfunctions ![]() satisfy
satisfy
![]() (5)
(5)
then the eigenfunctions ![]() form an orthonormal basis of
form an orthonormal basis of![]() .
.
From [8] , we know that the unique solution of problem (1) can be expressed as
![]() (6)
(6)
where ![]() denotes the inner product in
denotes the inner product in![]() .
.
Setting![]() , use the mean value theorem of integrals, for every fixed t, there exists some points
, use the mean value theorem of integrals, for every fixed t, there exists some points![]() , such that
, such that
![]() (7)
(7)
from (5) and the integration formula by parts, we know
![]() (8)
(8)
thus, the solution (6) can be rewritten as
![]() (9)
(9)
From (9), it can be observed that ![]() tends to infinity as n tends to infinity, so in order
tends to infinity as n tends to infinity, so in order
to recovery the stability of solution ![]() given by (6), the coefficient
given by (6), the coefficient ![]() must decay rapidly. However, such a decay usually cannot occur for the measured data
must decay rapidly. However, such a decay usually cannot occur for the measured data![]() , thus we have to use a regularization technique to restore numerical stability.
, thus we have to use a regularization technique to restore numerical stability.
2.2. The Description of Iteration Method
In this subsection, we give our iteration method. Firstly, given ![]() as an initial guessed value for
as an initial guessed value for![]() , this method consist in solving the parabolic type equation
, this method consist in solving the parabolic type equation
![]() (10)
(10)
this is a direct problem, use the similar method as in [8] , we can derive that the solution of problem (10) can be expressed as
![]() (11)
(11)
Now, for![]() , let us choose a positive constant r, we need to solve the direct problem sequence of parabolic type equation
, let us choose a positive constant r, we need to solve the direct problem sequence of parabolic type equation
![]() (12)
(12)
then, for![]() , we can obtain the solution of problem (12) is as follow
, we can obtain the solution of problem (12) is as follow
![]() (13)
(13)
Take![]() , such that
, such that![]() , and denote
, and denote
![]() , then combine with (13), we can obtain the following iteration scheme
, then combine with (13), we can obtain the following iteration scheme
![]() (14)
(14)
Let the exact and noisy data ![]() and satisfy
and satisfy
![]() (15)
(15)
where ![]() denotes the
denotes the ![]() -norm, the constant
-norm, the constant ![]() denotes a noise level. Then for the noisy data
denotes a noise level. Then for the noisy data![]() , the iteration scheme can be expressed by
, the iteration scheme can be expressed by
![]() (16)
(16)
and we note that
![]() (17)
(17)
Now, we truncate (16) to obtain the following our iterative algorithm
![]() (18)
(18)
where N is a positive constant, which plays a role of the regularization parameter.
For simplicity, we take the initial guess as zero, then our iterative scheme becomes
![]() (19)
(19)
Further, we suppose that there exists a constant![]() , such that the following a-priori bound holds
, such that the following a-priori bound holds
![]() (20)
(20)
3. Convergence Estimate
3.1. An A-Priori Stopping Rule
In the iterative process, the iterative step number k can be chosen by the a-priori and a-posteriori rules. In this subsection, we choose it by an a-priori rule and give the convergence estimate for the iterative algorithm.
Theorem 3.1. Suppose that u given by (6) is the exact solution of problem (1) with the exact data ![]() and
and ![]() is the iteration solution defined by (19) with the measured data
is the iteration solution defined by (19) with the measured data![]() . Let the measured data
. Let the measured data ![]() satisfy (15), and the a priori bound (20) is satisfied. If we choose the iteration step number
satisfy (15), and the a priori bound (20) is satisfied. If we choose the iteration step number![]() , then for fixed
, then for fixed![]() , we have the following convergence estimate
, we have the following convergence estimate
![]() (21)
(21)
Proof. For![]() , we define two functions
, we define two functions![]() , and
, and![]() . Now we have the following two important inequalities [16] [17] .
. Now we have the following two important inequalities [16] [17] .
![]() (22)
(22)
![]() (23)
(23)
where
![]() (24)
(24)
Use the triangle inequality, it is clear that
![]() (25)
(25)
From the Equations (6), (19) with the exact data![]() , by the mean value theorem of integrals as in (7) of Subsection 2.1 and the integration by parts (8), and from the inequality (23), (24) with
, by the mean value theorem of integrals as in (7) of Subsection 2.1 and the integration by parts (8), and from the inequality (23), (24) with![]() , a-priori bound (20), and
, a-priori bound (20), and![]() , one can obtain that
, one can obtain that
![]()
On the other hand, from the Equation (19) with the exact and measured data![]() ,
, ![]() which satisfy (15), the inequality (22) with
which satisfy (15), the inequality (22) with![]() , the mean value theorem of integrals as in (7) and the integration by parts (8), we can get
, the mean value theorem of integrals as in (7) and the integration by parts (8), we can get
![]()
From the above estimates of![]() ,
, ![]() , and the triangle inequality (25), we can obtain the convergence result (21).
, and the triangle inequality (25), we can obtain the convergence result (21).
3.2. An A-Posteriori Stopping Rule
In the iterative process, the a-priori stopping rule ![]() needs the a-priori bound E for exact solution. And from the proof process of Theorem 3.1 we can notice that, for the iterative scheme (19), if an a-priori bound E is known, the bigger iterative step number k is, the better the iterative efficiency should be. However, a-priori bound generally can be not known, this is unfortunate for numerical computation. In order to make the convenient and accurate computation, instead of a-priori selection in Theorems 3.1, below we adopt the discrepancy principle [18] to control it, which is a kind of a-posteriori stop rule and the computation of iterative step number k does not need to know the a-priori bound of the exact solution.
needs the a-priori bound E for exact solution. And from the proof process of Theorem 3.1 we can notice that, for the iterative scheme (19), if an a-priori bound E is known, the bigger iterative step number k is, the better the iterative efficiency should be. However, a-priori bound generally can be not known, this is unfortunate for numerical computation. In order to make the convenient and accurate computation, instead of a-priori selection in Theorems 3.1, below we adopt the discrepancy principle [18] to control it, which is a kind of a-posteriori stop rule and the computation of iterative step number k does not need to know the a-priori bound of the exact solution.
For the iterative scheme (19), we control the iterative step number k by the following form
![]() (26)
(26)
where ![]() is a constant,
is a constant, ![]() denotes the first iterative step which satisfies the first inequality of (26).
denotes the first iterative step which satisfies the first inequality of (26).
Theorem 3.2. Suppose that u given by (6) is the exact solution of problem (1) with the exact data ![]() and
and ![]() is the iteration solution defined by (19) with the measured data
is the iteration solution defined by (19) with the measured data ![]() which satisfy (15). If the a priori bound (20) is satisfied and the iterative step
which satisfy (15). If the a priori bound (20) is satisfied and the iterative step ![]() is chosen by (26), then for fixed
is chosen by (26), then for fixed![]() , we have the following convergence estimate
, we have the following convergence estimate
![]() (27)
(27)
Proof. Firstly, for the estimate of![]() , adopting the similar procedure as in Theorem 3.1, from the inequality (22) with
, adopting the similar procedure as in Theorem 3.1, from the inequality (22) with![]() , (15), we have
, (15), we have
![]()
Below, we estimate![]() . From the scheme (19), the first inequality of stopping rule (26), and the orthogonal property of
. From the scheme (19), the first inequality of stopping rule (26), and the orthogonal property of![]() , it can be noted that
, it can be noted that
![]() (28)
(28)
then, we get
![]() (29)
(29)
Now, from the Equations (6), (19) with the exact data![]() , by the mean value theorem of integrals as in (7) and the integration by parts (8), and from the inequalities (23), (24) with
, by the mean value theorem of integrals as in (7) and the integration by parts (8), and from the inequalities (23), (24) with![]() , (29), a-priori bound (20), one can derive that
, (29), a-priori bound (20), one can derive that
![]()
From the above estimates of ![]() and
and![]() , the convergence result (27) can be obtained.
, the convergence result (27) can be obtained.
Remark 3.3.
For the a-priori case, in problem (1) and the inequality (2), if we take ![]() and choose
and choose
![]() ,
,
then it can be obtained that
![]()
Note that, ![]() , then it can be derived the following order optimal convergence result [19]
, then it can be derived the following order optimal convergence result [19]
![]() (30)
(30)
where
![]() .
.
Similarly, for the a-posteriori case, we can derived the convergence result of order optimal
![]() (31)
(31)
where![]() .
.
4. Numerical Implementations
In this section, we use a numerical example to verify how this method works. Since the ill-posedness for the case at ![]() is stronger than the case of
is stronger than the case of![]() , here we are only interested in the reconstruction of the initial data
, here we are only interested in the reconstruction of the initial data![]() .
.
Example. We take![]() , and consider the following direct problem
, and consider the following direct problem
![]() (32)
(32)
where![]() ,
, ![]() with the domain
with the domain![]() , its eigenvalue and the eigenfunction are
, its eigenvalue and the eigenfunction are![]() ,
, ![]() , respectively.
, respectively.
As in (10), (11), the solution of problem (32) can be written as
![]() (33)
(33)
here,![]() . We choose the exact data as
. We choose the exact data as
![]() (34)
(34)
and the measured data ![]() is given by
is given by![]() , where
, where ![]() is the error level.
is the error level.
In addition, we define the relative root mean square errors (RRMSE) between the exact and approximate solution is given by
![]() (35)
(35)
In order to make the convenient and accurate computation, we adopt the a-posteriori stopping rule (26) to choose the iterative step k. During the computation procedure, we take![]() ,
, ![]() to compute the iterative solution
to compute the iterative solution ![]() by (19) with
by (19) with![]() .
.
For![]() , the numerical results for
, the numerical results for![]() ,
, ![]() constructed from
constructed from ![]() with
with ![]() are shown in Figure 1. For
are shown in Figure 1. For![]() , the numerical results for
, the numerical results for![]() ,
, ![]() constructed from
constructed from ![]() are shown in Figure 2. For the constructed case from
are shown in Figure 2. For the constructed case from![]() , the relative root mean square errors (RRMSE) and iterative number k with
, the relative root mean square errors (RRMSE) and iterative number k with ![]() are shown in Table 1.
are shown in Table 1.
From Figure 1, Figure 2 and Table 1, we can see that our proposed method is stable and feasible. Figure 1 indicates that, with the increase of T, the construction effects become worse, this is because the information of final data will become less when T becomes big. From Figure 2 and Table 1, we note that the smaller the ![]() is, the better the computed efficiency is. This is a normal phenomena in the backward heat conduction problem (BHCP).
is, the better the computed efficiency is. This is a normal phenomena in the backward heat conduction problem (BHCP).
5. Conclusion
An iterative method is based on the truncated technique to solve a BHCP with variable coefficients. Under an a- priori and an a-posteriori selection rule for the iterative step number, the convergence estimates are established. Some numerical results show that this method is stable and feasible.
Acknowledgements
The authors appreciate the careful work of the anonymous referee and the suggestions that helped to improve the paper. The work is supported by the the SRF (2014XYZ08), NFPBP (2014QZP02) of Beifang University of Nationalities, the SRP of Ningxia Higher School (NGY20140149) and SRP of State Ethnic Affairs Commission of China (14BFZ004).
NOTES
![]()
*Corresponding author.