New Theory of Superconductivity. Magnetic Field in Superconductor. Effect of Meissner and Ochsenfeld ()

Subject Areas: Computational Physics, Theoretical Physics

1. Introduction
Kamerlingh and Onnes were those who could discover the phenomenon of superconductivity in 1911 [1] . According to the results obtained in 1933 it was found out that when a specimen was put in a relatively weak magnetic field, the superconductivity vanished. Such phenomenon was discovered by Meissner and Ochsenfeld [2] . Magnetic field strength Hc at which superconductivity is destroyed is known as the critical field. Temperature dependence on the critical field is described by the following empirical formula:
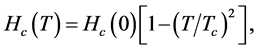 (1.1)
(1.1)
where 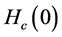 is the magnetic field strength at absolute zero of temperature T = 0; Tc is a critical temperature. The dependence (1.1) is plotted in Figure 1.
is the magnetic field strength at absolute zero of temperature T = 0; Tc is a critical temperature. The dependence (1.1) is plotted in Figure 1.
The plane (H, T) is represented by a superconductive state phase diagram. The substance in superconductive state S is found under the curve (1.1) and that to be in normal state N―above the curve. Any superconductor introduced by such state diagram is known as the type-I superconductor.
Brothers Fritz and Heinz London could develop the first macroscopic theory of superconductivity in 1935 [3] . They mathematically formulated the theory based on principal experimental factors: absence of resistance and the Meissner-Ochsenfeld effect:
 (1.2)
(1.2)
These facts were acknowledged a priori. For the superconductor magnetic field, the brothers obtained the following equation:
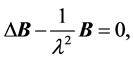 (1.3)
(1.3)
where
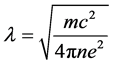
Value l is called a London length of the magnetic field penetration in a superconductor.
Let us consider a superconductor occupying the half-space y > 0, then the region y < 0 is filled with vacuum where a magnetic field B0 can be found as directed along the boundary surface (see Figure 2). In this case, the Equation (1.3) can be expressed as follows:
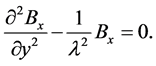 (1.4)
(1.4)
The Equation (1.4) may be expressed as follows:
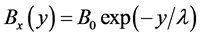 (1.5)
(1.5)
![]()
Figure 1. The H-T type-I superconductive state phase diagram.
![]()
Figure 2. The half-space filled by a superconductor in a magnetic field.
It should be noted that such function does not agree with the Meissner-Ochsenfeld effect. When magnetic- field strength produced on conductor surface exceeds its critical value Hc(T), the superconductivity vanishes. But, on the whole, the function (1.5) does not depend on any critical field.
The Meissner-Ochsenfeld effect is an experimental fact. If the function (1.5) does not depend on the critical field, then the Londons theory is not true. Moreover, the superconductivity shall be referred to equilibrium state of any matter, i.e. all values are not to be dependent on time t. But the very dependences can be used for deriving the London’s equation.
2. Density Matrix
Any quantum mechanics system can be much closely described by using the density matrix [4] - [12] . The single- particle density matrix  meets the following normalizing condition:
meets the following normalizing condition:
 (2.1)
(2.1)
where 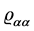 is the occupation probability for a particle to be in state α.
is the occupation probability for a particle to be in state α.
The two-particle density matrix 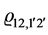 with figures 1, 2, 1′, and 2′ denoting states
with figures 1, 2, 1′, and 2′ denoting states 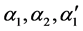 and
and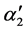 , as to be referred to the fermion system, is an antisymmetric function, i.e.
, as to be referred to the fermion system, is an antisymmetric function, i.e.
![]() (2.2)
(2.2)
Taking into account the above equality let us use the following approximate expression named as the mean field approximation for the two-particle density matrix:
![]() (2.3)
(2.3)
3. Energy of an N-Particle Fermion System
Internal energy of the identical particle system may be exactly expressed through the use of the density matrices ![]() and
and ![]() as follows:
as follows:
![]() , (3.1)
, (3.1)
where ![]() and
and ![]() are matrix elements of the single-particle Hamiltonian
are matrix elements of the single-particle Hamiltonian ![]() and two-particle interaction Hamiltonian
and two-particle interaction Hamiltonian![]() , respectively. Whereas the two-particle density matrix is antisymmetric, it follows from the expression (2.2) that the matrix elements
, respectively. Whereas the two-particle density matrix is antisymmetric, it follows from the expression (2.2) that the matrix elements ![]() are to be antisymmetric, as well:
are to be antisymmetric, as well:
![]() (3.2)
(3.2)
The coordinate representation to which the Hamiltonians commonly assigned passes to a certain α-represen- tation through the use of system of the orthonormal wave functions![]() , where q = {r, ξ}, ξ is a particle spin. If we know these functions, we can calculate matrix elements for Hamiltonians by using the known formulas:
, where q = {r, ξ}, ξ is a particle spin. If we know these functions, we can calculate matrix elements for Hamiltonians by using the known formulas:
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
where the above sign of integration is a symbol of both the coordinate integration and spin variable summation; Φ12 is a Slater two-particle wave function:
![]() (3.5)
(3.5)
On substituting such function in the formula (3.4), we can obtain an antisymmetric matrix as follows:
![]() (3.6)
(3.6)
where
![]() (3.7)
(3.7)
![]() is a potential dual-fermion interaction energy.
is a potential dual-fermion interaction energy.
With the expression (2.3) substituted in the formula (3.1), the following formula may be obtained:
![]() (3.8)
(3.8)
that agrees with the mean field approximation.
4. Unitary Transformation
Any single-particle density matrix may be represented by a diagonal element and, particularly, it can be formulated as follows:
![]() (4.1)
(4.1)
where n is a set of quantum numbers that defines state of newly represented single particle; ![]() is a parameter of diagonal density matrix elements;
is a parameter of diagonal density matrix elements; ![]() is a Kronecker symbol. Subject to the definition, function
is a Kronecker symbol. Subject to the definition, function ![]() is the probability that the state n can be occupied by one of the particles. Accordingly, function
is the probability that the state n can be occupied by one of the particles. Accordingly, function ![]() describes the pattern applicable to distribution of particles over various states and meets the following normalizing condition:
describes the pattern applicable to distribution of particles over various states and meets the following normalizing condition:
![]() (4.2)
(4.2)
The n-representation passes to the α-representation to which specific matrix elements of the Hamiltonians ![]() and
and ![]() are assigned by means of the unitary transformation.
are assigned by means of the unitary transformation.
![]() (4.3)
(4.3)
where ![]() is a unitary matrix;
is a unitary matrix;
![]() (4.4)
(4.4)
Now, we transform the energy (3.8) by the formula (4.3) to obtain the expression below:
![]() (4.5)
(4.5)
where
![]() (4.6)
(4.6)
―n-state kinetic particle energy,
![]() (4.7)
(4.7)
―double-particle interaction energy containing one n-state particle and another n′-state particle;
![]()
![]() (4.8)
(4.8)
5. Entropy
If to use the distribution function![]() , the following well-known approximate expression may be applied for the entropy of fermion systems:
, the following well-known approximate expression may be applied for the entropy of fermion systems:
![]() (5.1)
(5.1)
6. Variational Principle
For finding the fermion state distribution function![]() , we can formulate a particular extremum functional of the problem. And we can employ the Langrange method defined by its thermodynamic potential:
, we can formulate a particular extremum functional of the problem. And we can employ the Langrange method defined by its thermodynamic potential:
![]() (6.1)
(6.1)
where μ is a chemical potential. The variational principle may be expressed as follows for the distribution function![]() :
:
![]() (6.2)
(6.2)
where ![]() is mean one-particle energy:
is mean one-particle energy:
![]() (6.3)
(6.3)
7. Unitary Electron Matrix in the Crystal Lattice
The arrangement of atoms within a given type of crystal can be described in terms of the Bravais lattice with location of the atoms in an isolated unit cell specified. We will determine position of one of the atoms in the unit cell using vector R. Such description agrees with simple crystal lattices including those where type-I superconductivity can be observed. Let us consider s as a set of quantum numbers defining the wave function of one of the states of a valence electron located within the neighborhood of the atom, the position of which is determined by vector R. Now, we can write the orthonormal system of wave functions that describe localized electron states by using the form shown below:
![]() (7.1)
(7.1)
where![]() ,
, ![]() is a Wannier coordinate s-function;
is a Wannier coordinate s-function; ![]() is a spin function;
is a spin function;![]() ― is a set of quantum numbers defining state of an electron in the crystal lattice. The function (7.1) satisfies the normalizing conditions as follows:
― is a set of quantum numbers defining state of an electron in the crystal lattice. The function (7.1) satisfies the normalizing conditions as follows:
![]() (7.2)
(7.2)
The normalizing condition (7.2) may be expressed by:
![]() (7.3)
(7.3)
![]() (7.4)
(7.4)
Should a system of electrons in metal be brought to a state of thermodynamic equilibrium, any of the States ![]() in site R may be occupied by an electron of equal probability and such electrons will be nearly uniformly distributed among lattice sites. In this case, the density matrix will take the following form:
in site R may be occupied by an electron of equal probability and such electrons will be nearly uniformly distributed among lattice sites. In this case, the density matrix will take the following form:
![]() (7.5)
(7.5)
The probability ![]() of the state
of the state ![]() to be occupied by an electron is related to a diagonal matrix density element by the ratio of
to be occupied by an electron is related to a diagonal matrix density element by the ratio of![]() . In this case,
. In this case,
![]() (7.6)
(7.6)
where ![]() is the probability of filling of one state in site R.
is the probability of filling of one state in site R.
Let is assume that number of electron states localized in site R, as described by the Wannier functions![]() , is as follows:
, is as follows:![]() . As far as
. As far as![]() , the normalizing condition
, the normalizing condition
![]()
is formulated as follows:
![]() (7.7)
(7.7)
where NL is number of crystal lattice sites,
![]() (7.8)
(7.8)
―degree of state filling,
![]() (7.9)
(7.9)
―number of states within one site.
Let us assume the density matrix ![]() to be expressed in the form of complex Fourier series:
to be expressed in the form of complex Fourier series:
![]() (7.10)
(7.10)
where the summation is performed by using wave vectors k of the first Brillouin zone; wk is a wave-vector electron distribution function that satisfies the following normalizing condition:
![]() (7.11)
(7.11)
It follows from the equalities (7.5) and (7.10) that the density matrix ![]() can be transformed to its diagonal form by applying the unitary matrix as follows:
can be transformed to its diagonal form by applying the unitary matrix as follows:
![]() (7.12)
(7.12)
Thus, the density matrix ![]() is transformed to the following one:
is transformed to the following one:
![]() (7.13)
(7.13)
where![]() . And the probability
. And the probability
![]()
that the state κ, as described by the wave function![]() , is occupied, may be expressed as:
, is occupied, may be expressed as:
![]() (7.14)
(7.14)
8. Equation for the Electron Wave-Vector Distribution Function
Let us write the Equation (6.2) for the electron wave-vector distribution function![]() :
:
![]() (8.1)
(8.1)
where ![]() is a mean single electron energy to have the wave vector k:
is a mean single electron energy to have the wave vector k:
![]() (8.2)
(8.2)
The expression for two-electron and wave vector k and k′ interaction energy ![]() has been derived in the paper [13] :
has been derived in the paper [13] :
![]() , (8.3)
, (8.3)
herein, we use I and J that have particular dimension energy. Let us substitute this expression in the formula (8.2). Now, we will obtain as follows:
![]() . (8.4)
. (8.4)
Using the above formula (8.4) it is possible to transform the Equation (8.1) as follows:
![]() (8.5)
(8.5)
This equation describes all superconductor properties [14] - [25] .
9. Solution of the Equation for the Electron Wave-Vector Distribution Function when J = 3I
The Equation (8.5) contains two unknown quantities―i.e. ![]() and
and![]() . Let us interchange k and ?k.
. Let us interchange k and ?k.
Taking into account that any kinetic energy is an even function:![]() , we can obtain the following equation:
, we can obtain the following equation:
![]() (9.1)
(9.1)
As applies to the equations (8.5) and (9.1), the unknown functions wk and w−k are composite ones wherein the kinetic electron energy εk is used as an intervening variable:
![]() (9.2)
(9.2)
The functions
![]() and
and ![]()
are solutions of the equations
![]() (9.3)
(9.3)
where
![]() (9.4)
(9.4)
is expressed by the I and J energy relation as defined by the following parameter:
![]() (9.5)
(9.5)
In this Section, we will consider the case when parameter J = 3I. Wherein f = 1/2.
Any solutions of the Equations (9.3) may be rapidly found by computation. A plot of the w(ε, τ) distribution function is demonstrated in Figure 3 that satisfies τ = 0 and parameters J = 3I. Should the functions ![]() and
and ![]() be unequal, an anisotropic solution is required. With temperature being increased, an anisotropic solution starts decreasing and thereafter it disappears but should such temperature be rated as equal to a critical value, than:
be unequal, an anisotropic solution is required. With temperature being increased, an anisotropic solution starts decreasing and thereafter it disappears but should such temperature be rated as equal to a critical value, than:
![]() (9.6)
(9.6)
10. Electron Energy Computation at T = 0
As shown in Figure 3, the wave-vector electron equilibrium distribution function may be both anisochromic and multi-valued. The function with the electron energy to be of the least value may be only selected out of a number of other functions. Now, let us calculate the energy exhibited by electrons to be distributed both isotropically and anisotropically. For this purpose, we shall use the normalizing condition that may be expressed as:
![]() (10.1)
(10.1)
The electron system energy in approximation of a medium field takes the form as follows:
![]() (10.2)
(10.2)
If the distribution function ω = ω(ε) is known, it is possible to find a chemical potential and electron energy at T = 0. Such computation results have been demonstrated in the papers [13] - [25] . The macrostate in which electron energy is minimized can be actually applied. At T = 0, energy drops down to its minimum rate as specified for the state formulated below:
![]() (10.3)
(10.3)
This function is featured with anisotropy at![]() . A pattern of this function is plotted in Figure 4.
. A pattern of this function is plotted in Figure 4.
11. Electrons in the Superconductive State
Taking into account normalizing conditions, we can express the average electron travel velocity as follows:
![]() (11.1)
(11.1)
If the distribution function is isotropic, the average velocity of electron v will be zero. As applies to some anisotropic functions, the distributed formula (11.1) may produce nonzero electron directed motion velocity
![]()
Figure 3. Anisotropic conduction electron energy distribution function in case when J = 3I and at τ = 0.
![]()
Figure 4. Anisotropic conduction electron energy distribution function in case when J = 3I and at τ = 0.
values ? i.e. such distribution functions are those that describe electric current. If current states are rather stable and can exist even in the absence of any external fields such traveling electron system states are to be considered as superconductive.
Let us view the state of electron gas to be described by the anisotropic distribution function (10.3). Any value taken on by the average electron velocity function may be determined against the nature of initial electron gas state. The average velocity will be zero when pairs of free and occupied states (with vectors k and ?k) are distributed over the layer S randomly, i.e. no supercurrent flow will be induced in a conductor at![]() . For example, let us consider the probability
. For example, let us consider the probability ![]() at
at ![]() when T = 0. Since vector
when T = 0. Since vector ![]() is found in the region
is found in the region![]() , the probability
, the probability ![]() at
at![]() . This also holds true for the probability
. This also holds true for the probability ![]() and
and ![]() at
at![]() . Should vectors
. Should vectors ![]() and
and ![]() be randomly distributed over the region S, the average electron velocity will be zero:
be randomly distributed over the region S, the average electron velocity will be zero:![]() The wave vectors
The wave vectors ![]() and
and![]() , as randomly distributed over the region S, are shown in Figure 5 with probabilities
, as randomly distributed over the region S, are shown in Figure 5 with probabilities ![]() and
and![]() .
.
When all the states to be considered in one half of the layer S (e.g. at![]() ) are occupied and those in another half (at
) are occupied and those in another half (at![]() ) are free, the electron directed motion velocity will be brought to maximum
) are free, the electron directed motion velocity will be brought to maximum![]() . If the anisotropic wave-vector electron distribution function remains stable against slight variation of external conditions, the electron velocity value will be kept unchanged as long as it is can. This means that the metal becomes a superconductor.
. If the anisotropic wave-vector electron distribution function remains stable against slight variation of external conditions, the electron velocity value will be kept unchanged as long as it is can. This means that the metal becomes a superconductor.
The distribution function should be single-valued. This means that a single distribution function value corre- sponds to a single energy value. As concerns the anisotropic distribution function, it shall be a double-valued one. It simultaneously defines two k and ?k wave vector values that agree with two values of the distribution function ![]() and
and![]() . But the matter is that such vectors may also agree with
. But the matter is that such vectors may also agree with ![]() and
and![]() . This may be to say that it is the very superconduction phenomenon.
. This may be to say that it is the very superconduction phenomenon.
For detecting any superconductivity, low current flow is supplied along a conductor. Then, temperature is decreased. A circuit should be closed when temperature drops below a specified value. Steady current is conserved and keeps flowing as long as it can. Let us consider that current flows along axis x. The pattern of the k wave-vector space electron distribution function at T = 0 is shown in Figure 6.
12. Mean Electron Energy
Dependence ![]() of the electron mean energy
of the electron mean energy ![]() on the kinetic energy
on the kinetic energy ![]() can be found by the formula (8.4):
can be found by the formula (8.4):
![]() (12.1)
(12.1)
![]() (12.2)
(12.2)
Such dependence, as rated at various temperature τ values, is graphically represented in Figure 7.
The above curves are featured with the following specific characteristics. A “well” is demonstrated on each curve of the dependence ![]() at
at ![]() wherein it agrees with values of the kinetic energy ε that satisfies the following inequalities:
wherein it agrees with values of the kinetic energy ε that satisfies the following inequalities:
![]()
Figure 6. Electron distribution function for a substance subject to current flow.
![]() . (12.3)
. (12.3)
Value ![]() is specified as the least one of those of the kinetic electron energy ε wherefrom the functions
is specified as the least one of those of the kinetic electron energy ε wherefrom the functions ![]() and
and ![]() can be determined. Value
can be determined. Value ![]() satisfies the condition:
satisfies the condition:
![]() (12.4)
(12.4)
according to which borders of the “well”, as demonstrated on the curve of dependence![]() , are brought to the same level. The function is broken off at the right-hand border of the above well. This means that there is a certain “gap” in the spectrum of values of the electron energy
, are brought to the same level. The function is broken off at the right-hand border of the above well. This means that there is a certain “gap” in the spectrum of values of the electron energy![]() . The gap width ∆ is extended from zero to value J when temperature falls down from Tc to zero. With the temperature decreased, the well width
. The gap width ∆ is extended from zero to value J when temperature falls down from Tc to zero. With the temperature decreased, the well width
![]() (12.5)
(12.5)
is also extended from zero to value I at T = 0.
13. Magnetic Field-Induced Behavior of the Wave Function
Let us find the wave function ![]() from the Schrödinger equation:
from the Schrödinger equation:
![]()
Figure 7. Dependence of the mean electron energy ![]() on the kinetic energy
on the kinetic energy ![]() at various temperature values τ: 1―τ = 0; 2―τ = 0.75; 3―τ = 0.95.
at various temperature values τ: 1―τ = 0; 2―τ = 0.75; 3―τ = 0.95.
![]() (13.1)
(13.1)
where ![]() is a single-particle Hamiltonian that describes motion of one electron less interaction with other electrons. As for us, we are interested in motion of a valence electron in the metal.
is a single-particle Hamiltonian that describes motion of one electron less interaction with other electrons. As for us, we are interested in motion of a valence electron in the metal.
Since an electron has a spin, the Hamiltonian ![]() in a magnetic field will be formulated as:
in a magnetic field will be formulated as:
![]() (13.2)
(13.2)
where ![]() is a spin magnetic moment of an electron;
is a spin magnetic moment of an electron; ![]() is a Bohr magneton; ξ = ±1/2 is an electron spin; U(r) is potential electron energy; H is magnetic-field strength.
is a Bohr magneton; ξ = ±1/2 is an electron spin; U(r) is potential electron energy; H is magnetic-field strength.
![]() (13.3)
(13.3)
where![]() ,
, ![]() is a coordinate function; R is a vector that defines an ion around which an electron moves;
is a coordinate function; R is a vector that defines an ion around which an electron moves; ![]() is a spin function,
is a spin function,![]() .
.
Let us write the Schrödinger equation for the wave function![]() :
:
![]() (13.4)
(13.4)
and on substituting the product (13.3), we will obtain:
![]()
If the coordinate function satisfies the equation
![]() (13.5)
(13.5)
than a spin function shall be used for solving the following equation:
![]() (13.6)
(13.6)
where
![]() (13.7)
(13.7)
As follows from the Equation (13.6), the proper value ![]() will take up:
will take up:
![]() (13.8)
(13.8)
As a result, we will obtain:
![]() (13.9)
(13.9)
Now, we will accept the functions ![]() as equal to each other:
as equal to each other:
![]() (13.10)
(13.10)
where![]() . The spin functions are different only. Therefore, we well have two functions:
. The spin functions are different only. Therefore, we well have two functions:
![]() (13.11)
(13.11)
where![]() .
.
Let us consider the energies possessed by an electron when its spin is valued differently. As follows from the formula (13.9), when an electron spin is equal to -1/2, its energy is taken as
![]()
and when an electron spin is equal to 1/2, its energy is taken as
![]()
Thus,
![]()
Therefore, the probability ![]() when an electron has the spin taken as 1/2 exceeds the probability
when an electron has the spin taken as 1/2 exceeds the probability ![]() when an electron has the spin taken as −1/2:
when an electron has the spin taken as −1/2:
![]() .
.
14. Kinetic Energy of Electrons in the Crystal Lattice
Let us consider that two values of electron energy, as determined by the formula (13.9), correspond to each of the states specified in site R. So, matrix elements of the single-particle Hamiltonian may be expressed as:
![]() (14.1)
(14.1)
As a result, we will obtain:
![]()
Since
![]() (14.2)
(14.2)
here ![]() is the particle energy produced when passing from site R to site R′. As applies to spin functions, the normalizing condition will take up the following form:
is the particle energy produced when passing from site R to site R′. As applies to spin functions, the normalizing condition will take up the following form:
![]() (14.3)
(14.3)
In this case
![]()
where
![]()
Thus, the following formula is obtained:
![]() (14.4)
(14.4)
15. Magnetic Field-Dependent Unitary Transformation
As applies to the coordinate function (13.11) the normalizing condition will take up the following form:
![]() (15.1)
(15.1)
when a system of electrons in metal is at the state of thermodynamic equilibrium, any of the states ![]() in site R may be occupied by an electron of equal probability and such electrons will be nearly uniformly distributed among lattice sites. Need to say that this is not absolutely true. As follows from the formula (14.4), the probabilities, as referred to those intended to occupy any states with various spin orientation, are different from each other. But we will ignore such differences. As a matter of fact the density matrix will take the following form:
in site R may be occupied by an electron of equal probability and such electrons will be nearly uniformly distributed among lattice sites. Need to say that this is not absolutely true. As follows from the formula (14.4), the probabilities, as referred to those intended to occupy any states with various spin orientation, are different from each other. But we will ignore such differences. As a matter of fact the density matrix will take the following form:
![]() (15.2)
(15.2)
As such, the density matrix ![]() is transformed to take the diagonal form through the use of the unitary matrix:
is transformed to take the diagonal form through the use of the unitary matrix:
![]() (15.3)
(15.3)
where ![]() and the density matrix
and the density matrix ![]() pass to the matrix as follows:
pass to the matrix as follows:
![]() (15.4)
(15.4)
The probability ![]() that state κ―i.e. that one described by the wave function
that state κ―i.e. that one described by the wave function![]() ―is occupied can be expressed as:
―is occupied can be expressed as:
![]() (15.5)
(15.5)
16. The Energy of Electrons in the Wave Vector Space
Let us substitute the formula (14.4) in the following expression for noninteracting electron energy:
![]()
Upon simple transformation we can obtain the formula shown below:
![]() (16.1)
(16.1)
Now, we write:
![]() (16.2)
(16.2)
where
![]() (16.3)
(16.3)
Let us write the energy E1 as follows:
![]() (16.4)
(16.4)
The interacting electron energy will take up the below form:
![]() (16.5)
(16.5)
where an appropriate electron interaction energy will be formulated as:
![]()
On summing up the energies (16.4) and (16.5), we will obtain the following electron energy expression:
![]() (16.6)
(16.6)
17. Equation for the Electron Wave-Vector Distribution Function
On minimizing the thermodynamic potential Ω, as referred to the energy (16.6), we obtain the following nonlinear equation to be applied for finding the distribution function ![]() of wave-vector conduction electrons:
of wave-vector conduction electrons:
![]() (17.1)
(17.1)
Let us consider
![]() (17.2)
(17.2)
than the Equation (17.1) will take up its previous solution:
![]() (17.3)
(17.3)
Let us consider, for example,![]() . As follows from (17.2), we will obtain the expression
. As follows from (17.2), we will obtain the expression![]() .
.
This means that a curve of the electron wave-vector distribution function is displaced on its right by value Λ as compared with the graphical representation without a magnetic field. As follows from the Equation (17.3), the critical temperature is equal to:
![]()
18. Electron Energy Calculation at T = 0
As provided by computational results, the equilibrium distribution function applicable in a wave-vector region is multiple-valued. For selecting a real distribution function, it is necessary to find the least electron energy. Now, we shall consider the case when a magnetic field destroys the superconductivity at T = 0. Let us
![]() . (18.1)
. (18.1)
The graphical representation of the distribution function is displaced on its write by the above value (see Figure 8).
We can bring the upper integration level to ∞ since the probability of occupancy of states with the energy ε to be at a ceiling of the conductivity zone is virtually equal to zero. Now, the normalizing condition (10.1) may be expressed as:
![]() (18.3)
(18.3)
In such a case any energy of electrons (10.2) distributed isotropically may be expressed as:
![]()
The superconductivity disappears when the distribution function is taken as:
![]() (18.4)
(18.4)
As a result, we can obtain the following normalizing condition:
![]() (18.5)
(18.5)
Thus
![]() (18.6)
(18.6)
where ![]() is a Fermi energy. Any valence electron energy specified at J = 3I may be calculated as:
is a Fermi energy. Any valence electron energy specified at J = 3I may be calculated as:
![]() (18.7)
(18.7)
On calculating the above integral we will obtain:
![]()
![]()
Figure 8. Real conduction electron distribution over energies at τ = 0. The superconductivity-affected magnetic field is in active state.
As a result, the following formula is derived:
![]() (18.8)
(18.8)
But such superconducting state may in any way survive and the distribution function takes up the form as:
![]() (18.9)
(18.9)
As applies to the normalizing condition, the equation takes up the form as:
![]() (18.10)
(18.10)
The equation gives the following chemical potential:
![]() (18.11)
(18.11)
An electron energy may be calculated by the formula:
![]()
Let us suppose that J = 3I and Λ = I. And the following form will be obtained:
![]() (18.12)
(18.12)
As provided by the above equation, we can obtain:
![]() (18.13)
(18.13)
Now, we can find the difference in energy:
![]() (18.14)
(18.14)
As we can see, the energy of state ![]() to be induced under the superposition of the superconductivity―affected magnetic field occurs to be less than the superconductivity state energy
to be induced under the superposition of the superconductivity―affected magnetic field occurs to be less than the superconductivity state energy![]() :
:
![]() (18.15)
(18.15)
This means that the superconductivity can vanish under magnetic field effect when its strength, as defined on a surface of a superconductor, is equal to a critical field. This condition meets Meissner-Ochsenfeld effect.
19. Meissner-Ochsenfeld Effect
Let us consider that parameter Λ is equal to I. In this case, the distribution pattern is displaced on its right. Now, we can find the critical magnetic-field strength, as rated at T = 0, through the use of the formulas (16.2) and (18.1):
![]() (19.1)
(19.1)
If temperature τ exceeds zero, the critical magnetic-field strength subject to the formula (16.2) is formulated as:
![]() (19.2)
(19.2)
where ![]() is a width of the potential well (12.5) on the mean electron energy dependence of its kinetic energy.
is a width of the potential well (12.5) on the mean electron energy dependence of its kinetic energy.
With the graphical representation of the mean electron energy dependence applied against its kinetic energy shown in Figure 7, it is possible to plot the critical magnetic-field dependence of temperature. For the above graphical representation (refer to Figure 1). If to compare the plots demonstrated in Figure 1 and Figure 9 with the dependence of the critical-field strength considered against that of the theoretical one it can be seen that they match to each other.
By what way does the width of the energy well behave at constant temperature (τ = const), provided that the external magnetic-field strength jumps from zero to value H? In case of absence of the magnetic field, the width of a well will be rated at![]() . When the magnetic field of the strength H is produced on a superconductor surface, the kinetic energy (17.2) is displaced on its right by a certain value. In this case, energy wells are not subject to variation but displaced on their right. It is possible to assume that the electron energy will take up the least value when some portion of a well is displaced by value
. When the magnetic field of the strength H is produced on a superconductor surface, the kinetic energy (17.2) is displaced on its right by a certain value. In this case, energy wells are not subject to variation but displaced on their right. It is possible to assume that the electron energy will take up the least value when some portion of a well is displaced by value![]() . Thus, the superconducting well width is represented by the formula:
. Thus, the superconducting well width is represented by the formula:
![]() (19.3)
(19.3)
Let us substitute ![]() in the Equation (19.3) by using the formula (19.2). Now, we will obtain:
in the Equation (19.3) by using the formula (19.2). Now, we will obtain:
![]() (19.4)
(19.4)
When the magnetic-field strength H is equal to the critical value![]() , the superconducting well width will be brought to zero.
, the superconducting well width will be brought to zero.
20. Supercurrent
Any superconductor current flow is featured with its density matrix shown in Figure 6. Mean electron velocity is:
![]() (20.1)
(20.1)
Now, we substitute the sum (20.1) for the following integral:
![]() (20.2)
(20.2)
Using the above formula, we calculate mean velocity for T = 0 with the formula (18.2) considered as true.
This formula makes it possible to find radii k1 and k2 of the spheres shown in Figure 6:
![]()
As a result, we will obtain as follows:
![]()
The layer thickness, as specified in Figure 6, will be approximately equal to:
![]() (20.3)
(20.3)
In case of absence of external magnetic fields, when an electron distribution pattern is described by the formula (18.9), the largest value of mean electron velocity produced in the flow of supercurrent will be formulated as:
![]() (20.4)
(20.4)
As it is follows the respective electric current density vector can be expressed as:
![]() (20.5)
(20.5)
With the external magnetic field applied while its strength is kept on the level of less than the critical value, the following mean electron velocity can be obtained:
![]()
If to substitute the formula (19.4), we will obtain the expression shown below:
![]() (20.6)
(20.6)
Now, the current flowing along the superconductor will have the density determined by the current velocity (20.6):
![]()
As a result, we obtain the formula expressed as:
![]() (20.7)
(20.7)
where![]() . When the external field strength exceeds its critical value, the superconductivity vanishes and the density vector will be determined by the substance conductivity ρ.
. When the external field strength exceeds its critical value, the superconductivity vanishes and the density vector will be determined by the substance conductivity ρ.
21. Magnetic Field in the Superconductor
It is need to remind that we investigate equilibrium state of the superconductor. Time independent functions are to be considered only in this state. These functions satisfy the equations expressed as:
![]() (21.1)
(21.1)
![]() (21.2)
(21.2)
Let us consider the magnetic field effect produced on a planar border of the superconductor, provided that the magnetic field vector H runs parallel to the border. We arrange axes x lengthwise the conductor border and parallel to vector H and axis y―perpendicularly to the border (see Figure 10).
In this case, the Equation (21.1) takes up the form as:
![]() (21.3)
(21.3)
Since any superconducting current is produced by a negative component ![]() of vector J:
of vector J:
![]()
substituting the value (20.7) in this equation we will obtain the formula expressed as:
![]() (21.4)
(21.4)
where
![]() (21.5)
(21.5)
In view of the superposition principle, the magnetic field vector H can be considered as equal to the sum of the external and magnetic fields to be created by supercurrents:
![]() (21.6)
(21.6)
Let us consider that any supercurrent flowing along axis z, as demonstrated in Figure 10, is produced in a substance with the external magnetic field absent:
![]()
Such current may flow along the superconductor as long as it can. As concerns to electrons, they achieve their mean velocity. The supercurrent produces am self-magnetic field featured with the strength of ![]() that satisfies the equation as:
that satisfies the equation as:
![]()
Figure 10. Layout of the coordinate axes lengthwise the planar border of the superconductor. Currents produced by superconducting electrons are graphically represented here.
![]() (21.7)
(21.7)
Any strength produced by the supercurrent will be equal to zero at the superconductor border:
![]() (21.8)
(21.8)
Since the strength satisfies the very condition it can be expressed as:
![]() (21.9)
(21.9)
For the graphical representation of this function (see Figure 11).
Now, we create the external magnetic field running lengthwise axis x with its strength represented by
![]() . It is evident that the above field strength may have any alternate mark:
. It is evident that the above field strength may have any alternate mark: ![]() or
or
![]() . The self-magnetic field of the superconductor is added to a just created field as specified by the principle of superposition. Therefore, the complete field will be formulated as:
. The self-magnetic field of the superconductor is added to a just created field as specified by the principle of superposition. Therefore, the complete field will be formulated as:
![]() (21.10)
(21.10)
Let us substitute the complete field (21.10) in the Equation (21.4). We will obtain the formula shown below:
![]() . (21.11)
. (21.11)
We subtract the Equation (21.7) from the Equation (21.11). And the following external field equation is obtained:
![]() (21.12)
(21.12)
The external field strength, as determined at the border of the superconductor, will be equal to the given value ±H0 to be subject to change throughout an experiment:
![]() (21.13)
(21.13)
Since the function ![]() satisfies the starting condition it can be formulated as follows:
satisfies the starting condition it can be formulated as follows:
![]() (21.14)
(21.14)
This function is graphically represented in Figure 12. Here the value (21.14) is positive:
![]()
Thus, we could obtain the strength of the external magnetic field going down inside the superconductor. The
![]()
Figure 11. The self-magnetic field produced by supercurrent.
![]()
Figure 12. External magnetic field penetrating inside the superconductor.
complete field (21.10) is equal to the magnetic field produced by supercurrent and to the external field, provided that ![]() takes up the form as follows:
takes up the form as follows:
![]() (21.15)
(21.15)
When the external field strength takes up the following form
![]() (21.16)
(21.16)
the function (21.15) will be equal to the critical field:
![]() (21.17)
(21.17)
With ![]() subsequently increased, the self-magnetic field vanishes and the complete field strength will be equal to that of the external field:
subsequently increased, the self-magnetic field vanishes and the complete field strength will be equal to that of the external field:
![]() (21.18)
(21.18)
So, it is proved that when value H0 belongs to the interval
![]() (21.19)
(21.19)
the superconductivity will be applicable in the conductor under the Meissner-Achsenfeld effect. But if value ![]() exceeds the critical one:
exceeds the critical one:
![]() (21.20)
(21.20)
the superconductivity vanishes.
We have viewed in details the case when the strengths ![]() and
and ![]() of the external and self-magnetic fields runs in the same direction. And this is time to consider the strengths being directed differently. So we can obtain the following formula:
of the external and self-magnetic fields runs in the same direction. And this is time to consider the strengths being directed differently. So we can obtain the following formula:
![]() (21.21)
(21.21)
At![]() , this function will take up the form:
, this function will take up the form:
![]() .
.
As follows from the above, the Meissner-Ochsenfeld effect cannot be applicable. To remedy such condition, it is necessary to specify the external field as that changing direction of supercurrent flow. Thus, the direction of the superconductor self-magnetic field vector is considered as that matching the direction of the external magnetic field strength. As provided by the given calculations, the external magnetic field goes down inside the superconductor thanks to presence of the magnetic field produced by supercurrent.
Using the formula (20.7), let us find the supercurrent density as dependent on coordinate y. We substitute the formula (21.15) in the formula (20.7). As a result, we will obtain the following formula:
![]() (21.22)
(21.22)
where
![]()
As follows form the above formula, the density of current goes down from the superconductor border to an exponent. In case when the external magnetic field is absent (H0 = 0), the density will be equal to
![]() (21.23)
(21.23)
At![]() , the supercurrent density vanishes:
, the supercurrent density vanishes:
![]() (21.24)
(21.24)
22. Magnetic Field in the Spherical Superconductor
Let us now consider behavior of the magnetic field both inside and outside a spherically shaped superconductor. The superconductor at T > Tc, in case of absence of the superconductivity, is demonstrated in Figure 13.
In case when the temperature is brought to the level of below the critical value ? i.e. T < Tc, superconductivity is created in the superconductor. This very case is shown in Figure 14. Such a pattern exists till an external field has the strength less than that of the critical field. If the strength exceeds that of the critical field, the superconductivity vanishes and the pattern shown in Figure 13 is applied. Both the self-magnetic field and external field vectors have the same orientation.
Now, we will deactivate the external magnetic field in the state when temperature is less than the critical one: T < Tc. In this case, the superconductivity it is not vanished. The supercurrent is not changed but remains the same as before. And the structure of self-magnetic field lines is to be changed just a little (see Figure 15).
23. Quantum Capture and Quantum Levitation
Let is consider the quantum capture effect. Such capture effect is produced by any permanent magnet fixed at the constant height level. A disk-shaped superconductor is positioned below it less any supports. For a graphical layout (see Figure 16).
Let us assume that the external field vector H(external), superconductor self-magnetic field vector H(c) and superconductor magnetic moment vector Pm have the same orientation. According to the physical theory it is
![]()
Figure 13. External magnetic field produced in the superconductor at T >Tc.
![]()
Figure 14. Magnetic field in the conductor at T < Tc; the external magnetic field is forced out of the superconductor and its strength gets less than that of the critical field:![]() .
.
![]()
Figure 15. Self-magnetic field in the conductor pro- duced by supercurrent at T < Tc; no external magnetic field is applied.
![]()
Figure 16. Quantum superconductor capture at T < Tc.
known that in this case the potential superconductor energy produced in an external field will be equal to the following:
![]() (23.1)
(23.1)
The superconductor obtains the capacity to move in the space. The strength that makes effect on the superconductor is coupled with its potential energy formulated as follows:
![]() (23.2)
(23.2)
The external magnetic field is not homogeneous by nature and it has excess magnetic induction near a permanent magnet. Any force acting on the superconductor will make it move to those space regions wherein the energy (23.1) is reduced. If we direct the external magnetic field oppositely, it makes the supercurrent flow being reoriented to another direction along with the self-magnetic field. Thus, the external magnetic field, self- magnetic field and vector Pm will have the same orientation with the strength remained unchanged.
As provided by (23.1), the superconductor has the energy reduced at those areas where magnetic induction is exceeded. Therefore, the superconductor will be pulled into the region where an external field is stronger than that in other regions at x > x0, where x is a distance from a permanent magnet to the superconductor, x0 is an equilibrium position of the superconductor.
According to the formula (21.22) the supercurrent density will be approximately equal to as follows:
![]() (23.3)
(23.3)
where ![]() is a distance from the superconductor center to its edges; r is a radial coordinate;
is a distance from the superconductor center to its edges; r is a radial coordinate; ![]() is a external magnetic field strength on the superconducting disk surface edge. The external field strength
is a external magnetic field strength on the superconducting disk surface edge. The external field strength ![]() is increased while approaching to the permanent magnet till to the condition when it may be even equal to the critical field
is increased while approaching to the permanent magnet till to the condition when it may be even equal to the critical field![]() . In this case, the current density will be equal to zero. As a matter of fact, the superconductivity vanishes, the superconductor self-magnetic field is also brought to zero, and the superconductor fails pulling to the magnet but falls down. Therefore, the potential superconductor energy U(x) may have the approximate pattern demonstrated in Figure 17. While the superconductor is spaced off the permanent magnet, its potential energy exhibits an increasing function. On approaching it the permanent magnet its potential energy exhibits a decreasing function. The dependence of strength on the distance is graphically represented in Figure 18.
. In this case, the current density will be equal to zero. As a matter of fact, the superconductivity vanishes, the superconductor self-magnetic field is also brought to zero, and the superconductor fails pulling to the magnet but falls down. Therefore, the potential superconductor energy U(x) may have the approximate pattern demonstrated in Figure 17. While the superconductor is spaced off the permanent magnet, its potential energy exhibits an increasing function. On approaching it the permanent magnet its potential energy exhibits a decreasing function. The dependence of strength on the distance is graphically represented in Figure 18.
The graph in Figure 18 explains thequantum trappingof the superconductor. As can be seenfrom Figure 18, the strength of the superconductorreturnsto the position where![]() . This is thepositionof stable equilibrium superconductor, when heis in a stateof quantumtrapping.
. This is thepositionof stable equilibrium superconductor, when heis in a stateof quantumtrapping.
Now consider thequantumlevitation, when the superconductoris located above thefixedpermanent magnet (see. Figure 19).
The potential energy when![]() , which has a superconductor in an external field is determined by formula (23.1). The graphpotential energy are shown in Figure 20. Now let’s see how it will behave in a superconductor, when
, which has a superconductor in an external field is determined by formula (23.1). The graphpotential energy are shown in Figure 20. Now let’s see how it will behave in a superconductor, when![]() . Superconducting current is equal to (23.3). When the superconductor close to a permanent mag-
. Superconducting current is equal to (23.3). When the superconductor close to a permanent mag-
![]()
Figure 19. Quantum levitation of a superconductor at T < Tc.
![]()
Figure 20. The potential energy of a superconductor.
net, the value of ![]() decrease of xincreases and tends to the critical value of the
decrease of xincreases and tends to the critical value of the![]() . But until the moment when the current is zero, the magnetic moment of the superconductor
. But until the moment when the current is zero, the magnetic moment of the superconductor ![]() decreases. Consequently, the potential energy is the largest magnitude and becomes an increasing
decreases. Consequently, the potential energy is the largest magnitude and becomes an increasing
function (see Figure 20).
Differentiating the potential energy in xand from (23.2), we construct a graph of the power of location. The graphpower is shown in Figure 21. The strength of the superconductor is always striving to return to the position![]() , where the force is zero. This is the position of stable equilibrium.
, where the force is zero. This is the position of stable equilibrium.
24. Conclusions
The electron model in metal, as described in this paper, may be used as a basis of an alternative superconductivity theory. Such model significantly varies from those ones applied in the modern superconductivity theory.
![]()
Figure 21. The force acting onthe superconductor.
Here, the superconductivity is caused by repulsion of k and −k wave vector electrons but electron pairs and energy gap―by attracting of equal wave vector electrons. Such electrons are statically described in scope of a particular density matrix formalism featured with its simplicity typical for the appearance of mathematical formulas and their physical content. The problem under consideration demonstrates advantages of the density matrix method.
Influence of magnetic field effects on the superconductor has been studied in the context of this theory. The following aspects have been proved:
1. Any magnetic field is able to displace the electron wave vector distribution function pattern towards increased kinetic energy values.
2. The critical magnetic field ![]() is directly proportional to the energy well width δ ε.
is directly proportional to the energy well width δ ε.
3. It has been found that there are dependences on penetration of the supercurrent external field strength and self-magnetic field strength into the superconductor.
4. The dependence of the supercurrent density on the depth of penetration, temperature, and strength of external and critical fields has been found.