Size of the Electron Microparticle Calculated from the Oersted Law ()
Received 31 May 2016; accepted 5 July 2016; published 8 July 2016

1. Introduction
In order to obtain any classical property of an elementary microparticle, say the electron, an approach combined of both the quantum and classical physical laws seems to be necessary. In the present case―when the classical size parameter of the electron particle is aimed to be deduced―the quantum aspects can be provided by the Bohr model of the hydrogen atom. Here―for any quantum state―we have a definite orbital motion of a single electron in the electrostatic field of a positively charged proton nucleus. The motion―beyond of its orbital track ―has well-defined velocity and energy parameters. However, in order to make use of the equations of classical electrodynamics, especially the Maxwell equations, knowledge of the magnetic field―together with the electric field―in the atom seems to be necessary.
However both of the Maxwell equations―that consider the change of the magnetic induction and that concern the electric line current only (by assuming that the displacement current can be neglected)―take into account the time parameter on different footing [1] - [4] . In the first equation the time action is reduced to the use of a short interval representing the derivative of the magnetic flux with respect to time; in the second equation the time interval enters solely the current velocity, which can be assumed to be a constant term along an arbitrarily long quantity of time. This produces a stationary electric current whose charge density 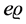 satisfies the equation
satisfies the equation
 (1)
(1)
If we assume the Bohr theory as valid for the hydrogen atom, the electric current given by the one-electron orbital motion is fully stationary for any chosen quantum level n. The velocity of the current composed of a single electron particle is [5]
 (2)
(2)
since
 (3)
(3)
is the orbit length and
 (4)
(4)
is the time period necessary to travel the distance 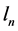 about the atomic nucleus.
about the atomic nucleus.
The aim of the present paper is, in the first step, to point out that the Maxwell equation concerning the electric line current
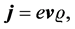 (5)
(5)
where  is the electron velocity and
is the electron velocity and 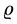 is the density of the electron particle, can be satisfied only when the microstructure properties of the electron particle are taken into account.
is the density of the electron particle, can be satisfied only when the microstructure properties of the electron particle are taken into account.
To this purpose we consider the quanta of the magnetic field  neglected in the original Bohr model [5] [6] . These quanta―introduced in Section 2―seem to be of importance (see [7] ) because they lead to the quanta of the magnetic flux identical with those known experimentally since a long time in superconductors [8] [9] . Moreover, a combination of the electric and magnetic field present in the atom gives the Poynting vector which approximately provides us with a proper rate of the energy emission due to the process of the electron transition between two quantum levels [10] . In Section 3 we show that the quanta
neglected in the original Bohr model [5] [6] . These quanta―introduced in Section 2―seem to be of importance (see [7] ) because they lead to the quanta of the magnetic flux identical with those known experimentally since a long time in superconductors [8] [9] . Moreover, a combination of the electric and magnetic field present in the atom gives the Poynting vector which approximately provides us with a proper rate of the energy emission due to the process of the electron transition between two quantum levels [10] . In Section 3 we show that the quanta  fulfill the Maxwell equation for the electric current with a satisfactory accuracy.
fulfill the Maxwell equation for the electric current with a satisfactory accuracy.
In the next step, in Section 4, the quanta of the magnetic field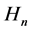 ―which are due to the electron orbital motion in the atom―are substituted into the equation representing the Oersted law:
―which are due to the electron orbital motion in the atom―are substituted into the equation representing the Oersted law:
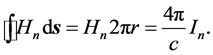 (6)
(6)
Here the path of  circumvents the circular cross-section area of the orbit, the area is assumed to have the radius r: it defines the surface of the orbital conductor at which the magnetic field is equal to
circumvents the circular cross-section area of the orbit, the area is assumed to have the radius r: it defines the surface of the orbital conductor at which the magnetic field is equal to  (see Figure 43 in Ref. [2] ). Since any orbit can be occupied solely by a single electron particle, r should be independent of the quantum index n. Symbol
(see Figure 43 in Ref. [2] ). Since any orbit can be occupied solely by a single electron particle, r should be independent of the quantum index n. Symbol ![]() in (6) represents the current intensity which is coupled with the circulation time period
in (6) represents the current intensity which is coupled with the circulation time period ![]() of the electron along the orbit n by the formula
of the electron along the orbit n by the formula
![]() (7)
(7)
It will be found that the indices n in (6) cancel together leaving the formula for the cross-section radius r of the orbit independent of n. This r is expected to approach the radius ![]() of the electron particle moving along the orbit.
of the electron particle moving along the orbit.
2. Maxwell Equation for the Electric Current and the Magnetic Field in the Hydrogen Atom
The Maxwell equation is written briefly in the form
![]() (8)
(8)
but it seems to be more convenient to apply an integral form of (8) which is
![]() (9)
(9)
The magnetic field ![]() in (9) is a constant term for a given n; see below. The length
in (9) is a constant term for a given n; see below. The length ![]() is given in (3). It should be noted that the integral on the left of (9) does not concern the dot product of
is given in (3). It should be noted that the integral on the left of (9) does not concern the dot product of ![]() and
and![]() , but is the integral of
, but is the integral of ![]() extended over the line having the length
extended over the line having the length ![]() [2] .
[2] .
The ![]() can be obtained as a result of a constant electric current on the level n if we note that the current is surrounding periodically the nucleus with the frequency
can be obtained as a result of a constant electric current on the level n if we note that the current is surrounding periodically the nucleus with the frequency
![]() (10)
(10)
where ![]() is given in (4). On the other hand, the
is given in (4). On the other hand, the ![]() is coupled with
is coupled with ![]() by the formula [7] [11]
by the formula [7] [11]
![]() (11)
(11)
This is an effect of the Lorentz force law in which the wave-vector ![]() of the electron particle satisfies the relation
of the electron particle satisfies the relation
![]() (11a)
(11a)
The last step in (11a) is due to the fact that the magnetic field is normal to the velocity vector along the orbit. For a full circulation time ![]() we have
we have![]() . Since
. Since ![]() we obtain from (11a) the relation
we obtain from (11a) the relation
![]()
identical with (11).
A substitution of ![]() from (4) into (10) gives together with (11) the equation
from (4) into (10) gives together with (11) the equation
![]()
from which we obtain
![]() (12)
(12)
It is interesting to note that ![]() in (12) can be obtained also from the theory of the cyclotron resonance in metals [11] . We have the relation [11]
in (12) can be obtained also from the theory of the cyclotron resonance in metals [11] . We have the relation [11]
![]()
where
![]() (13)
(13)
is the absolute electron energy in state n [5] , and
![]() (14)
(14)
is the area occupied by the electron orbit in that state. Here the constants ![]() and
and ![]() replace respectively the energy interval
replace respectively the energy interval ![]() and area interval
and area interval ![]() in the real space admitted in course of the change of the quantum state n. A substitution of
in the real space admitted in course of the change of the quantum state n. A substitution of ![]() from (13) and
from (13) and ![]() from (14) valid for the hydrogen atom gives together with the formula (11) for
from (14) valid for the hydrogen atom gives together with the formula (11) for ![]() the relation:
the relation:
![]()
This gives
![]()
which yields the square value of ![]() in (12).
in (12).
3. Current Analysis Done with the Aid of a Microstructure Parameter of the Electron Particle
Usually, when the electron is considered as a charged particle having the radius![]() , the potential energy of the charge extended on a spherical surface is assumed to be approximately equal to the rest energy of the electron [2] [12] :
, the potential energy of the charge extended on a spherical surface is assumed to be approximately equal to the rest energy of the electron [2] [12] :
![]() (15)
(15)
In effect
![]() (16)
(16)
The current (5) is composed, first, of the volume V occupied by the electron particle, so
![]() (17)
(17)
next the same current should move within a tube having a cross-section area equal approximately to
![]() (18)
(18)
Since the velocity ![]() for a given n is a constant [see (2)], we obtain for the right-hand side of (9) the formula
for a given n is a constant [see (2)], we obtain for the right-hand side of (9) the formula
![]() (19)
(19)
The left-hand side of (9) is
![]() (20)
(20)
A difference between the both sides of (9), or (19) and (20), is represented by the factor of 3/2.
4. The Quanta of the Magnetic Field and Time Periods Entering the Oersted Law Give the Radius of the Electron Microparticle
Any current is associated with the magnetic field and the lines of that field circumvent the line of the current. We assume that at the distance r from the center of the current cross-section area the field is ![]() for any orbit n. In this case the formulae (6) and (7) give the relation
for any orbit n. In this case the formulae (6) and (7) give the relation
![]() (21)
(21)
from which we obtain
![]() (22)
(22)
In effect the cross-section radius of the orbit which approximately can be identified with the radius of the electron microparticle becomes
![]() (23)
(23)
This result―evidently independent of the index n―is not much different than that given by the well-known formula (16) and the formula derived in [13] :
![]() (24)
(24)
5. Summary
The Maxwell equations, when applied to electrons, usually neglect the microsize parameters of the electron particle. In Appendix we demonstrate that the Poynting vector ![]() can be connected with the rest energy of the electron, therefore also with the radius r or
can be connected with the rest energy of the electron, therefore also with the radius r or![]() .
.
One of aims of the present paper was to indicate that these parameters can be essential in making the Maxwell equations satisfied for a given problem.
The Maxwell equation for the electric current has been examined for the case of the one-electron current present in the Bohr model of the hydrogen atom. It has been shown, for the magnetic field induced by the current, that the equation is satisfied on condition that the microstructure parameter of the electron radius ![]() is explicitly taken into account. Here an earlier result can be pointed out that the magnetic field strength
is explicitly taken into account. Here an earlier result can be pointed out that the magnetic field strength ![]() entering the Poynting vector constructed for the rate of the emission spectrum in the hydrogen atom cannot be reproduced from the Biot-Savart law unless the electron microstructure radius
entering the Poynting vector constructed for the rate of the emission spectrum in the hydrogen atom cannot be reproduced from the Biot-Savart law unless the electron microstructure radius ![]() is applied in the calculations (see [10] [14] [15] ).
is applied in the calculations (see [10] [14] [15] ).
But the size of the electron microradius can be of importance for itself, especially in quantum electrodynamics, so its calculation becomes a useful task. In the next step of the paper, a substitution of ![]() and
and![]() ―characte- ristic respectively for the magnetic field quanta and time periods of the electron circulation in the atom―into the Oersted formula gives the expression for the cross-section radius of the electron orbit equal to
―characte- ristic respectively for the magnetic field quanta and time periods of the electron circulation in the atom―into the Oersted formula gives the expression for the cross-section radius of the electron orbit equal to
![]() (25)
(25)
The result in (25), which can be identified with the size of the radius ![]() of the electron microparticle, does not differ much from the well-known formula (16) as well as the formula quoted in (24).
of the electron microparticle, does not differ much from the well-known formula (16) as well as the formula quoted in (24).
Appendix: Rest Energy of the Electron Mass Connected with the Poynting Vector of the Hydrogen Atom
The value of the Poynting vector for the energy emission in the hydrogen atom can be easily calculated with the aid of ![]() in (12) and the absolute value of the vector of the electric field intensity
in (12) and the absolute value of the vector of the electric field intensity![]() :
:
![]() (A1)
(A1)
where ![]() is the orbit radius applied in (2) and (3). For the spherical surface S having the radius
is the orbit radius applied in (2) and (3). For the spherical surface S having the radius![]() , so
, so
![]() (A2)
(A2)
we obtain the absolute value of the Poynting vector ![]() equal to
equal to
![]() (A3)
(A3)
The decrement of ![]() due to the change of the quantum state
due to the change of the quantum state ![]() into n for large n is equal to
into n for large n is equal to
![]() (A4)
(A4)
The time period ![]() of the electron circulation in state n of the hydrogen atom [see (4)] is entering the denominator of the last term in (A3) and (A4). This is a characteristic substitution of the transition time
of the electron circulation in state n of the hydrogen atom [see (4)] is entering the denominator of the last term in (A3) and (A4). This is a characteristic substitution of the transition time ![]() between two neighbouring quantum levels
between two neighbouring quantum levels ![]() and n in the hydrogen atom obtained in a quantum aspect of the Joule-Lenz energy dissipation theory [10] [16] :
and n in the hydrogen atom obtained in a quantum aspect of the Joule-Lenz energy dissipation theory [10] [16] :
![]() (A5)
(A5)
The emission rate (A4) can be compared with that given by the Joule-Lenz approach [10] [16] :
![]() (A6)
(A6)
We see that decrease of (A6) with increase of n is much more rapid than decrease of (A4). Moreover we have
![]() (A7)
(A7)
which makes any (A6) much smaller than (A4). The reason of the discrepancy seems to be the choice of S equal to (A2) instead of a much smaller S equal to the toroidal surface enclosing the orbit of the electron circulation about the nucleus.
In any way the Joule-Lenz approximation for the energy emission rate in the hydrogen atom works well as it is indicated by its comparison with the quantum-mechanical theory (see [17] [18] ).