Deceleration Parameter Q(Z) and Examining If a Joint DM-DE Model Is Feasible, with a Revisit to the Question of Cosmic Singularities ()
Received 29 April 2016; accepted 4 July 2016; published 8 July 2016

1. Introduction
We begin with a brief model as to singular universe, versus a multiverse in terms of input into singularity construction. The singularity behavior envisioned in this document is given by the following argument, as given by Kauffman [1] and the author in [2] , with the case of when one has been reevaluating the question of a “near singularity” in a multiverse. The multiverse will assume Ergotic mixing of space-time as given by [3] . Massless gravitons corresponds to the physics described in the beginMassless gravitons corresponds to the physics described in the beginning of the 2nd part of this document, whereas if massive gravitons exist, the resulting alterations of the general relativistic equations will be linking us to review questions as to if singularities exist at the start of cosmological expansion. Or, the start of cosmological expansions, if massive gravitons exist, assumes the existence of a small non singular regime of space-time. This sharply differentiates us from the physics given in reference [4] , as we explain in our document.
2. Review of the Formalism of Congruence or Lack of with Singularities If a Massive Graviton Exists, in Early Universe Geometry
We follow the recent work of Kauffmann [1] , which sets an upper bound to concentrations of energy, in terms of how he formulated the following equation put in below as Equation (1). Equation (1) specifies an inter-rela- tionship between an initial radius R for an expanding universe, and a “gravitationally based energy” expression we will call TG(r) which lead to a lower bound to the radius of the universe at the start of the Universe’s initial expansion, with manipulations. The term TG(r) is defined via (2) afterwards. We start off with Kauffmann’s expression [1]
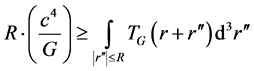 (1)
(1)
Kauffmann [1] calls 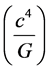 a “Planck force” which is relevant due to the fact we will employ (1) at the initial
a “Planck force” which is relevant due to the fact we will employ (1) at the initial
instant of the universe, in the Planckian regime of space-time. Also, we make full use of setting for small r, the following:
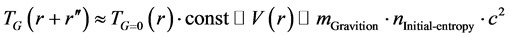 (2)
(2)
i.e. what we are doing is to make the expression in the integrand proportional to information leaked by a past universe into our present universe, with Ng [5] - [18] style quantum infinite statistics use of
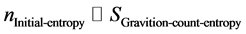 (3)
(3)
Then Equation (3) will lead to
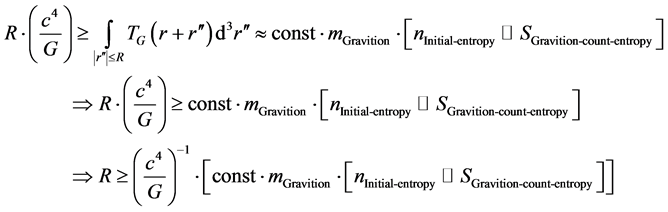 (4)
(4)
Here, 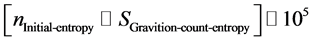 ,
, 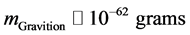 , and we set Planck length as:
, and we set Planck length as:
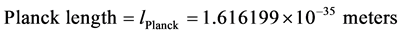 (5)
(5)
where we set 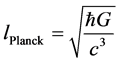 with
with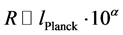 , and
, and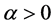 . Typically
. Typically  is about
is about 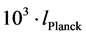 at
at
the outset, when the universe is the most compact. The value of const is chosen based on common assumptions about contributions from all sources of early universe entropy, and will be more rigorously defined in a later paper. We argue that the above methodology, giving a non zero initial starting point is made especially tend ible if one is using a low temperature start, allowing for the existence of prior recycling universes gravitons to play a role, i.e. that in the single universe repeated again and again, there would be real issues as to the survival of the graviton allowing for the conclusion as to Equation (4). What Equation (4) is doing is to help us determine if conditions exist for a massive graviton versus a massless graviton. If Equatuion (4) is consistent with the existence of massive gravitons, then our inflaton model contributes to models which have Dark Energy as due directly to the existence of massive gravitons in space-time.
3. Looking at Measuring Gravity Waves, and Gravitons, with Mass
We will start with a first-principle introduction to detection of gravitational wave density using the definition given by Maggiore [6]
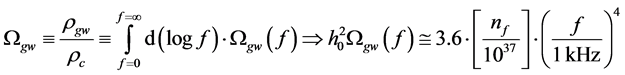 (6)
(6)
where 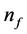 is the frequency-based numerical count of gravitons per unit phase space. The author suggests that
is the frequency-based numerical count of gravitons per unit phase space. The author suggests that ![]() may also depend upon the interaction of gravitons with neutrinos in plasma during early-universe nucleation, as modeled by M. Marklund et al. [7] . Having said that, the question is, what sort of mechanism is appropriate for considering macro effects of gravitons, and the author thinks that he has one, i.e. reacceleration of the universe, as far as a function of graviton mass, i.e. what Beck with is to modify is what was in reference [8] Assume Snyder geometry and look at use of the following inequality for a change in the HUP [8] ,
may also depend upon the interaction of gravitons with neutrinos in plasma during early-universe nucleation, as modeled by M. Marklund et al. [7] . Having said that, the question is, what sort of mechanism is appropriate for considering macro effects of gravitons, and the author thinks that he has one, i.e. reacceleration of the universe, as far as a function of graviton mass, i.e. what Beck with is to modify is what was in reference [8] Assume Snyder geometry and look at use of the following inequality for a change in the HUP [8] ,
![]() (7)
(7)
and that the mass of the graviton is partly due to the stretching alluded to by Fuller and Kishimoto [9] a supposition the author is investigating for a modification of a joint KK tower of gravitons, as given by Maartens [10] [11] for DM. Assume the stretching of early relic neutrinos that would lead to the KK tower of gravitons―for when![]() , is,
, is,
![]() (8)
(8)
Note that Rubakov [12] - [14] writes KK graviton representation as, after using the following normalization
![]() where
where ![]() are different forms of Bessel functions, to obtain the
are different forms of Bessel functions, to obtain the
KK graviton/DM candidate representation along RS dS brane world [12]
![]() (9)
(9)
This Equation (8) and Equation (9) is for KK gravitons having a TeV magnitude mass ![]() (i.e. for mass values at. 5 TeV to above a TeV in value) on a negative tension RS brane. What would be useful would be managing to relate this KK graviton, which is moving with a speed proportional to
(i.e. for mass values at. 5 TeV to above a TeV in value) on a negative tension RS brane. What would be useful would be managing to relate this KK graviton, which is moving with a speed proportional to ![]() with regards to the
with regards to the
negative tension brane with ![]() as an initial starting value for the KK graviton mass,
as an initial starting value for the KK graviton mass,
before the KK graviton, as a “massive” graviton moves with velocity ![]() along the RS dS brane. If so, and if
along the RS dS brane. If so, and if
![]() represents an initial state, then one may relate the mass of the KK graviton, moving
represents an initial state, then one may relate the mass of the KK graviton, moving
at high speed, with the initial rest mass of the graviton, which in four space in a rest mass configuration would have a mass lower in value, i.e. of![]() , as opposed to
, as opposed to![]() . Whatever the range of the graviton mass, it may be a way to make sense of what was presented by Dubovsky et al. [15] who argue for graviton mass using CMBR measurements, of
. Whatever the range of the graviton mass, it may be a way to make sense of what was presented by Dubovsky et al. [15] who argue for graviton mass using CMBR measurements, of ![]() Dubosky et al. [15] results can be conflated with Alves et al. [16] arguing that non zero graviton mass may lead to an acceleration of our present universe, in a manner usually conflated with DE, i.e. their graviton mass would be about
Dubosky et al. [15] results can be conflated with Alves et al. [16] arguing that non zero graviton mass may lead to an acceleration of our present universe, in a manner usually conflated with DE, i.e. their graviton mass would be about
![]() . Also assume that to calculate the deceleration, the following
. Also assume that to calculate the deceleration, the following
modification of the HUP is used: [2] ![]() , where the LQG condition is
, where the LQG condition is![]() ,
,
and brane worlds have, instead, ![]() Also (10) will be the starting point used for a KK tower version of (10) below. So from Maarten’s [10] [11] paper,
Also (10) will be the starting point used for a KK tower version of (10) below. So from Maarten’s [10] [11] paper,
![]() (10)
(10)
Maartens [10] [11] also gives a 2nd Friedman equation, as
![]() (11)
(11)
Also, we are in the regime for which ![]() for redshift values z between zero and 1.0 - 1.5 with exact equality of pressure being equal to the negative value of density,
for redshift values z between zero and 1.0 - 1.5 with exact equality of pressure being equal to the negative value of density, ![]() for redshift z between zero to 0.5. The net effect will be to obtain, due to (6), and use
for redshift z between zero to 0.5. The net effect will be to obtain, due to (6), and use
![]() . As given by Beckwith [17] [18]
. As given by Beckwith [17] [18]
![]() (12)
(12)
Equation (12) assumes![]() , and the net effect is to obtain, a substitute for DE, by presenting how gravitons with a small mass done with
, and the net effect is to obtain, a substitute for DE, by presenting how gravitons with a small mass done with![]() , even if curvature K = 0.
, even if curvature K = 0.
4. Consequences of Small Graviton Mass for Reacceleration of the Universe
In a revision of Alves et al. [16] , Beckwith [17] [18] used a higher-dimensional model of the brane world and Marsden [10] [11] KK graviton towers. The density ![]() of the brane world in the Friedman equation as used by Alves et al. [16] is use by Beckwith for a non-zero graviton [17] [18]
of the brane world in the Friedman equation as used by Alves et al. [16] is use by Beckwith for a non-zero graviton [17] [18]
![]() (13)
(13)
i.e. Equation (12), and Equation (13) above is making a joint DM and DE model, with all of. (13) being for KK gravitons and DM, and ![]() grams being a 4 dimensional DE. (11) is part of a KK graviton presentation of DM/DE dynamics. Beckwith [17] [18] found at z ~ 0.4, a billion years ago, that acceleration of the universe increased, as shown in Figure 1 [17] [18] .
grams being a 4 dimensional DE. (11) is part of a KK graviton presentation of DM/DE dynamics. Beckwith [17] [18] found at z ~ 0.4, a billion years ago, that acceleration of the universe increased, as shown in Figure 1 [17] [18] .
5. What If an Inflaton Partly Re-Emerges in Space-Time Dynamics? At z ~ 0.423?
Padmanabhan [19] [20] has written up how the 2nd Friedman equation as of (11), which for z ~ 0.423 may be simplified to read as [10] [11]
![]()
Figure 1. Reacceleration of the universe based on Beckwith [17] [18] (note that q < 0 if z < 0.423).
![]() (14)
(14)
Equation (14) would lead to an inflaton value of, when put in, for scale factor behavior as given by
![]() , of, for the inflatonand inflation of [19] [20]
, of, for the inflatonand inflation of [19] [20]
![]() (15)
(15)
Assuming a decline of![]() , Equation (15) yields [19]
, Equation (15) yields [19]
![]() (16)
(16)
As the scale factor of ![]() had time of the value of roughly
had time of the value of roughly
![]() have a power law relationship drop below
have a power law relationship drop below![]() , the inflaton took Equation (16)’s value which may have been a factor as to the increase in the rate of acceleration, as noted by the q factor, given in Figure 1. Note that there have been analytical work projects relating the inflaton, and its behavior to entropy via noting that inflation stopped when the inflaton field settled down into a lower lower energy state. The way to relate an energy state to the inflaton is, if
, the inflaton took Equation (16)’s value which may have been a factor as to the increase in the rate of acceleration, as noted by the q factor, given in Figure 1. Note that there have been analytical work projects relating the inflaton, and its behavior to entropy via noting that inflation stopped when the inflaton field settled down into a lower lower energy state. The way to relate an energy state to the inflaton is, if![]() , then in the early universe, one has a potential energy term of [19] [20]
, then in the early universe, one has a potential energy term of [19] [20]
![]() (17)
(17)
A situation where both ![]() grows smaller, and, temporarily,
grows smaller, and, temporarily, ![]() takes on Equation (16)’s value, even if the time value gets large, and also, if acceleration of the cosmic expansion is taken into account, then there is infusion of energy by an amount dV. The entropy
takes on Equation (16)’s value, even if the time value gets large, and also, if acceleration of the cosmic expansion is taken into account, then there is infusion of energy by an amount dV. The entropy![]() , will lead, if there is an increase in V, as given by Equation (17) a situation where there is an effective increase in entropy. If there is, as will be related to later, circumstances, where [5]
, will lead, if there is an increase in V, as given by Equation (17) a situation where there is an effective increase in entropy. If there is, as will be related to later, circumstances, where [5] ![]() number of graviton states [17] [18] as will be derived in Equation (17), then at least in higher dimensions, we have an argument that the re emergence of an inflaton, with a corresponding reduction of Equation (17) in magnitude may be part of gravitons playing a role in the re acceleration of the universe.
number of graviton states [17] [18] as will be derived in Equation (17), then at least in higher dimensions, we have an argument that the re emergence of an inflaton, with a corresponding reduction of Equation (17) in magnitude may be part of gravitons playing a role in the re acceleration of the universe.
6. Other than Five Dimensions for Cosmology? Problems Which Need Resolutions
If a way to obtain a graviton mass in four dimensions is done which fits in with the as given higher 5 dimensions specified by a slight modification of brane theory, or Maarten’s cosmological evolution [10] [11] equations, what benefits could this approach accrue for other outstanding problems in cosmology? The author, Beckwith, claims that due to the Friedmann equations, it would result in deceleration parameter q(z) similar to Figure 1 above. Snyder geometry for the four dimensional case with would specify Friedmann equations along the lines of ![]() in Equation (2) above. If one follows
in Equation (2) above. If one follows![]() , then the Friedmann equations appear as giving details to the following equation [21]
, then the Friedmann equations appear as giving details to the following equation [21]
![]() (18)
(18)
The construction done from sections 1 to 3 are for![]() . When
. When![]() , the claim is that almost all the complexity is removed
, the claim is that almost all the complexity is removed![]() , and what is left is a [21] treatment of the Friedmann equations, where he obtains, to first order, if
, and what is left is a [21] treatment of the Friedmann equations, where he obtains, to first order, if ![]() is a scalar field density,
is a scalar field density,
![]() (19)
(19)
and
![]() (20)
(20)
The interpretation of ![]() as a scalar field density [21] , and if one does as Alves et al. [16] uses Equation (7) above. We need to interpret the role of
as a scalar field density [21] , and if one does as Alves et al. [16] uses Equation (7) above. We need to interpret the role of![]() . In the LQG version, Equation (20) may be rewritten as follows: If conjugate momentum is in many cases, “almost” or actually a constant, using
. In the LQG version, Equation (20) may be rewritten as follows: If conjugate momentum is in many cases, “almost” or actually a constant, using ![]()
![]() (21)
(21)
Beckwith [17] [18] claims that the deceleration parameter q(z) incorporating Equation (19), Equation (20) and. Equation (21) should give much the same behavior as Figure 1 above. If so, then if one is differentiating between four and five dimensions by what is gained, in cosmology, one needs having it done via other criteria. The following is a real problem. As given by Maggiore [6] , the massless equation of the graviton evolution equation takes the form
![]() (22)
(22)
When![]() , the above becomes [6]
, the above becomes [6]
![]() (23)
(23)
The mismatch between these two equations, when![]() , is due to
, is due to ![]() as
as![]() ,
,
which is due to setting a value of ![]() The semi classical method by t’Hooft [22]
The semi classical method by t’Hooft [22]
[23] , using Equation (22) and Equation (23) is the solution. We generalize to higher dimensions the following diagram as given by Beckwith [24] [25] . Use an instanton- anti instanton structure, and t’Hooft [22] [23] equivalence classes along the lines of (24) below with equivalence class structure in the below wave functional to be set by a family of admissible values [24] [25] ![]()
![]() (24)
(24)
We state that the process of nucleation of a graviton at the initiation of space-time creation. is similar in part to what occurs in the instanton-anti instanton formulation of Figure 2, above. At the end of the document will be a supposition as to taking this analogy far more directly as to the nature of gravitons, as a future works project.
This discussion above, would be consistent upon having a graviton represented by not only Equation (24). If
one is adding the small mass of ![]() grams, with
grams, with ![]() grams, then the
grams, then the
problem being worked with is a source term problem of the form given by Peskins [26] as of the type
![]() (24a)
(24a)
![]()
Figure 2. The pop up effects of an intanton-anti-instanton in euclidian space [24] [25] .
This is, using the language Rubakov [12] put up equivalent to obtain,
![]() (24b)
(24b)
If ![]() is a constant, then the expression (24b) has delta functions. This is the field theoretic identification. Another way is to consider an instanton-anti instanton treatment of individual gravitons, and to first start with the supposed stretch out of gravitons to enormous lengths. Assuming
is a constant, then the expression (24b) has delta functions. This is the field theoretic identification. Another way is to consider an instanton-anti instanton treatment of individual gravitons, and to first start with the supposed stretch out of gravitons to enormous lengths. Assuming ![]() grams for gravitons in 4 dimensions, the supposition by Bashinsky [27] and Beckwith3 is that density fluctuations are influenced by a modification of cosmological density
grams for gravitons in 4 dimensions, the supposition by Bashinsky [27] and Beckwith3 is that density fluctuations are influenced by a modification of cosmological density ![]() in the Friedmann equations by the proportionality
in the Friedmann equations by the proportionality
factor given by Bashinsky [27] ,![]() . This proportionality factor for
. This proportionality factor for ![]() as
as
showing up in the Friedmann equations should be taken as an extension of results from Marklund et al. [7] , due to graviton-neutrino interactions as proposed by Marklund et al. [7] , where neutrinos interact with plasmons and plasmons interact with gravitons. Thereby implying neutrino-graviton interactions Also, graviton wavelengths have the same order of magnitude of neutrinos. Note, from Valev [28] ,
![]() (25)
(25)
Extending M. Marklund et al. [7] and Valev [28] , some gravitons may become larger14, i.e.
![]() (26)
(26)
A way to accommodate this wave length as to an instanton-anti instanton packaging of gravitons, was to start with an analogy between Giovannini, [29] from a least action version of the Einstein―Hilbert action for “quadratic” theories of gravity involving Euler-Gauss-Bonnet. Then Giovannini’s [28] Equation (6) corresponds to
![]() (26a)
(26a)
in Givannini [28] . Furthermore the similarity between Equation (26a) and ![]()
in Beckwith’s [24] [25] treatment with regards to density wave physics instantons is obvious. If ![]()
is part of representing a graviton as a kink-anti-kink combination, arising from a 5 dimensional line element, [28]
![]() (26b)
(26b)
The end result of this would be to have an instaton-anti instanton structure as to emergence of a massive graviton if noting, that there is the possibility of using t’Hoofts [17] [22] [23] classical embedding of “deterministic quantum mechanics” as a way to embed a nearly four dimensional graviton as having almost zero mass, in a larger non linear theory.
7. How DM Would Be Influenced by Gravitons
The interrelationship of structure of the profile of a DM cluster, with any perturbations DM density profile [29]
![]() (27)
(27)
As told to the author by Sabino Matarre [29] , in July, 2009, in Como Italy, the gravitational potential has, perturbatively speaking an additional term ![]() added to variations in the gravitational potential term which Matarre [29] gave as
added to variations in the gravitational potential term which Matarre [29] gave as
![]() (28)
(28)
It is suggested that the function ![]() is largely due to entropy variations, some of which occurred during relic GW/graviton production. Here the expression
is largely due to entropy variations, some of which occurred during relic GW/graviton production. Here the expression ![]() variations from gaussianity. Furthermore,
variations from gaussianity. Furthermore, ![]() is a linear Gaussian potential, and the overall gravitational potential is altered by inputs from
is a linear Gaussian potential, and the overall gravitational potential is altered by inputs from![]() . Note that neutrinos flavor physics oscillations are not very important in terms of
. Note that neutrinos flavor physics oscillations are not very important in terms of![]() , as specified in conversations. Beckwith had in September 23, 2009 in Erice with George Raffert [30] . Which leads to emphasizing the role of entropy pro- cesses due to graviton-neutrino physics, as
, as specified in conversations. Beckwith had in September 23, 2009 in Erice with George Raffert [30] . Which leads to emphasizing the role of entropy pro- cesses due to graviton-neutrino physics, as ![]() as written up by Beckwith [31] .
as written up by Beckwith [31] .
8. 1st Part of Massive Graviton Consequences
The real start to this investigation is to explain how and why the star HE0107-5240 could form with so little lithium in the first place [31] . As stated by Fuller et al. [9] neutrinos could interact with DM potential wells in ways Beckwith thinks could influence deviations from standard galaxy hierarchy formation models which will also have a counter part in deviations in the BBN nucleosynthesis of light elements, by examining the role of temperature fluctuations modeled on Equation (29) below, leading to fluctuations affecting BBN element rarity [31] .
![]() (29)
(29)
While Equation (29) above would have its maximum impact for regions as of about red shift![]() , the impact of Equation (29) would be as of red shifts
, the impact of Equation (29) would be as of red shifts![]() , with the corresponding
, with the corresponding ![]() influenced by Bashinsky’s [27] neutrino―gravition damping as stated by the coefficient of density fluctuation modified by
influenced by Bashinsky’s [27] neutrino―gravition damping as stated by the coefficient of density fluctuation modified by
![]() [27] . Note that
[27] . Note that ![]() would be larger than
would be larger than ![]() of Equation (28) and
of Equation (28) and
would be dominated by neutrino-graviton interactions, whereas ![]() would be dominated by graviton generated entropy, with neutrinos at
would be dominated by graviton generated entropy, with neutrinos at ![]() hitting DM directly. We submit that a graviton with a small rest mass may be more amendable to such interaction with neutrinos, and that in addition Equation (27), Equation (28) and Equation (29) may influence and affect structure formation as seen by the following diagram in Figure 1. Note that this is assuming that early universe interactions which we are talking about eventually play out and reach, with the re acceleration of the universe, as outlined in the 1st half of our document to also be indirectly responsible for the famous “halo merging tree diagram we call Figure 3 below. At or about when
hitting DM directly. We submit that a graviton with a small rest mass may be more amendable to such interaction with neutrinos, and that in addition Equation (27), Equation (28) and Equation (29) may influence and affect structure formation as seen by the following diagram in Figure 1. Note that this is assuming that early universe interactions which we are talking about eventually play out and reach, with the re acceleration of the universe, as outlined in the 1st half of our document to also be indirectly responsible for the famous “halo merging tree diagram we call Figure 3 below. At or about when
![]() begins to delineate the neutrino-GW interaction becoming a significant damping impact upon each other, one would be seeing variations from the usual structure formation, as given by the following diagram. [32] .
begins to delineate the neutrino-GW interaction becoming a significant damping impact upon each other, one would be seeing variations from the usual structure formation, as given by the following diagram. [32] .
We should keep in mind that the following holds, i.e. for flat space. That one will have Figure 3 in both flat and in curved space. Also note that, M. Marklund, G. Brodin, and P. K. Shukla [7] posted their own version of not only neutrino mass, as given by![]() , where the overall mass is set by Note, here, that the
, where the overall mass is set by Note, here, that the
![]()
Figure 3. How we obtain “bottom up” development of galactic super structure which duplicates a diagram given in reference [32] .
potential for where the frequency comes from is, here, is![]() , and, according to Eberle and Ringwald et al. [33] , may have lightest relic neutrino masses of the order of
, and, according to Eberle and Ringwald et al. [33] , may have lightest relic neutrino masses of the order of
![]() (30)
(30)
as opposed to, as given by D. Valev [34]
![]() (31)
(31)
where![]() , is a dimensionless Hubble constant, Very roughly put, for relic early universe conditions, one may be seeing that the neutrino has
, is a dimensionless Hubble constant, Very roughly put, for relic early universe conditions, one may be seeing that the neutrino has ![]() the effective mass than a graviton. Furthermore, for a neutrino we have
the effective mass than a graviton. Furthermore, for a neutrino we have
![]() (32)
(32)
This will tie in directly with a neutrino mass limit we state as [7]
![]() . (33)
. (33)
If, as if often expected in inflation, space becomes abruptly flat at the onset of inflation, then for a neutrino mass, as the ![]() will then lead to the following inequality [7] [31]
will then lead to the following inequality [7] [31]
![]() (34)
(34)
Now, how would variation from the above “halo Merging history tree”, partly due to the modulation, via entropy, of DM structure formation, due to GW/gravitons affecting DM profile affect the concentration for lithium in stars, and perhaps lead to the famous “lithium problem” being resolved? We are investigating it. But we do think that having a graviton with mass is affecting the particulars of the “halo mixing tree” diagram [32] .
9. 2nd Part of Massive Graviton Consequences
Beckwith [35] has concluded that the only way to give an advantage to higher dimensions as far as cosmology would be to look at if a fifth dimension may present a way of actual information exchange to give the following parameter input from a prior to a present universe, i.e. the fine structure constant, as given by [35]
![]() (35)
(35)
Equation (35) above is in tandem, with examining if the following holds, i.e. for the consistency of physical law, namely from cycle to cycle is there a preservation of Planck’s constant? Namely
![]() (35a)
(35a)
The wave length as may be chosen to do such an information exchange would be part of a graviton as being part of an information counting algorithm as can be put below, namely: Argue that when taking the log, that the 1/N term drops out. As used by Ng [5]
![]() (36)
(36)
This, according to Ng [5] , leads to entropy of the limiting value of, if ![]() will be modified by having the following done, namely after his use of quantum infinite statistics,
will be modified by having the following done, namely after his use of quantum infinite statistics,
![]() (37)
(37)
Eventually, the author hopes to put on a sound foundation what t’Hooft [22] [23] is doing with respect to t’Hooft [22] [23] deterministic quantum mechanics and equivalence classes embedding quantum particle structures. Doing so will answer the questions Kay [36] 29 raised about particle creation, and the limitations of the particle concept in curved and flat space, i.e. the global hyperbolic space time which is flat everywhere expect in a localized “bump” of curvature. Furthermore, if we have an initial universe count of gravitons as S (initial) ~1010 to at most S (initial) ~1020, we are assuming the existence of one operation per graviton. This one operation per graviton in the early universe may correspond to at least one unit of information per graviton, i.e. one unit of “information” per graviton is correlated directly with one “operation” per graviton. The operation in this case is likely the creation of initial gravitons, in the early universe. This datum needs experimental confirmation and is important to astro physics linkage of DE with DM, in the future. Equation (14) to Equation (17) if confirmed for Z ~ 0.423 may prove that higher dimensions are necessary for cosmology.
10. 3rd Massive Graviton Consequences, the Need to Find out the Border of the Introduction of Where Quantum Gravity Emerges from a Prior “Analog” Structure May, If Tied into Questions of Graviton Mass Determine If Multiple Universes Are Possible/Feasible
Beckwith [37] , in his FQXi document outlined a procedure where a graviton with mass may be indicative of the existence of multiple universes co existing. The details of the mapping of that multiple universe picture involve a transition from an analog physics (discrete, i.e. classical world picture) to one where octonian gravity is formed, i.e. a quantum picture as a pre cursor to quantum gravity. The existence of a small mass may mean the extension of quantum physics to a larger embedding/extension of quantum physics. Furthermore, keep in mind that tandem to that step of semi classical embedding of a graviton, that eventually we want to make explicit an idea by, T. Padmanabhan in DICE 2010 [38] , as to finding “atoms of space time” permitting a thermodynamic treatment of emergent structure similar to Gibbs treatment of statistical physics. i.e. for finding out if the following is possible, i.e. can an ensemble of gravitons, be used to construct an “atom” of space time congruent with relic GW. That is our ultimate end, as to our research. That would make our inquiry of the nature of gravitons most worthwhile. This idea was presented at DICE 2010, [39] and we would like to refine it in our future research work. This would be in tandem of adapting the Kiefer, Polarski, and Starobinsky [40] presentation of the evolution of relic entropy via the evolution of phase spaces, with ![]() being the ratio of “final (future)”/“initial” phase space volume, for k modes of secondary GW background. From “atoms of space time” treatment of early universe space time geometry according to [40]
being the ratio of “final (future)”/“initial” phase space volume, for k modes of secondary GW background. From “atoms of space time” treatment of early universe space time geometry according to [40]
![]() (38)
(38)
This lead to the author, Beckwith to derive the following a important for structure formation, note the following about what happens if ![]()
![]() (39)
(39)
i.e. especially if the degrees of freedom rises above![]() .
.
Note that ![]() at T ~ 100 KeV Unless the term for
at T ~ 100 KeV Unless the term for ![]() were absolutely enormous, and if
were absolutely enormous, and if![]() , then
, then ![]() could happen, which would be physically meaningless. The other situation is that there could be situations for which
could happen, which would be physically meaningless. The other situation is that there could be situations for which ![]() would be undefined, especially if
would be undefined, especially if ![]() were close to an equality. We state here unequivocally that Equation (38) and Equation (39) above are important, and that this has serious experimental import. Having said that, we will next go to what would be a way to determine if Gravitons can have mass (massive Gravitons). i.e. in the conclusions section, we radically extend the consequences if
were close to an equality. We state here unequivocally that Equation (38) and Equation (39) above are important, and that this has serious experimental import. Having said that, we will next go to what would be a way to determine if Gravitons can have mass (massive Gravitons). i.e. in the conclusions section, we radically extend the consequences if![]() , with a speculation as to what could happen as to dark matter and dark energy contributions, which we think is important to the matter of singularities and their purported connection to a multiverse. But before we get to that matter, we will examine the role of partition functions, in terms of background which will lead to several pages later, to
, with a speculation as to what could happen as to dark matter and dark energy contributions, which we think is important to the matter of singularities and their purported connection to a multiverse. But before we get to that matter, we will examine the role of partition functions, in terms of background which will lead to several pages later, to ![]() contributions, especially for the regime of values, say of 1100 to 1200, which we think has to be seriously looked at.
contributions, especially for the regime of values, say of 1100 to 1200, which we think has to be seriously looked at.
11. Working with a Partition Function Argument in the Case of a Multiverse
This section is to determine if gravitons have mass and backs the assertion made earlier that multiverse construction has massive gravitons. Note that this section is directly linked to the first part of this document, as to what was done by the author to extend Kauffman’s work [1] .
We assume that there are no fewer than N universes undergoing Penrose “infinite expansion” (Penrose, 2006) [41] - [43] contained in a mega universe structure. Furthermore, each of the N universes has black hole evaporation, with the Hawking radiation from decaying black holes. If each of the N universes is defined by a partition
function, called![]() , then there exist an information ensemble of mixed minimum information correlated as about
, then there exist an information ensemble of mixed minimum information correlated as about ![]() bits of information per partition function in the set
bits of information per partition function in the set![]() , so minimum information is
, so minimum information is
conserved between a set of partition functions per universe [44]
![]() (40)
(40)
However, there is non-uniqueness of information put into each partition function![]() . Furthermore
. Furthermore
Hawking radiation from the black holes is collated via a strange attractor collection in the mega universe struc-
ture to form a new big bang for each of the N universes represented by![]() . Verification of this mega
. Verification of this mega
structure compression and expansion of information with a non-uniqueness of information placed in each of the N universes favors ergodic mixing treatments of initial values for each of N universes expanding from a singularity beginning. The ![]() value, will be using
value, will be using![]() . How to tie in this energy expression, as in Equation (40) will be to look at the formation of a nontrivial gravitational measure as a new big bang for each of the N universes as by
. How to tie in this energy expression, as in Equation (40) will be to look at the formation of a nontrivial gravitational measure as a new big bang for each of the N universes as by ![]() the density of states at a given energy
the density of states at a given energy ![]() for a partition function. (Poplawski, 2011) [45]
for a partition function. (Poplawski, 2011) [45]
![]() . (41)
. (41)
Each of ![]() identified with Equation (41) above, are with the iteration for N universes (Penrose, 2006) [41] - [44] Then the following holds, namely [44]
identified with Equation (41) above, are with the iteration for N universes (Penrose, 2006) [41] - [44] Then the following holds, namely [44]
Claim 1, [44]
![]() (42)
(42)
For N number of universes, with each ![]() for j = 1 to N being the partition function of each
for j = 1 to N being the partition function of each
universe just before the blend into the RHS of Equation (42) above for our present universe. Also, each of the
independent universes given by ![]() are constructed by the absorption of one to ten million
are constructed by the absorption of one to ten million
black holes taking in energy. i.e. (Penrose, 2006) [41] - [44] . Furthermore, the main point is similar to what was done in [18] in terms of general ergodic mixing
Claim 2 [44]
![]() (43)
(43)
Claim 3 The idea here is to use what is known as CCC cosmology [41] - [44] .
First. Have a big bang (initial expansion) for the universe. After red shift z = 10, a billion years ago, SMBH formation starts. Matter-energy is vacuumed up by the SMBHs, which at a much later date than today (present era) gather up all the matter-energy of the universe and recycles it in a cyclic conformal translation, as follows, namely
![]() (44)
(44)
![]() (45)
(45)
![]() is a constant. Then the main methodology in the Penrose proposal has been in Equation (45) evaluating a change in the metric
is a constant. Then the main methodology in the Penrose proposal has been in Equation (45) evaluating a change in the metric ![]() by a conformal mapping
by a conformal mapping ![]() [43] [44] to
[43] [44] to
![]() (46)
(46)
Penrose’s suggestion has been to utilize the following [43]
![]() (47)
(47)
Infall into cosmic black hopes has been the main mechanism which the author asserts would be useful for the recycling apparent in Equation (47) above with the caveat that ![]() is kept constant from cycle to cycle as represented by a restatement of Equation (35a) as in the multiverse as
is kept constant from cycle to cycle as represented by a restatement of Equation (35a) as in the multiverse as
![]() (48)
(48)
Equation (47) is to be generalized, as given by a weighing averaging as given by Equation (42) where the averaging is collated over perhaps thousands of universes, call that number N, with an ergodic mixing of all these universes, with the ergodic mixing represented by Equation (42) to generalize Equation (47) from cycle to cycle.
12. Why This Just Outlined Multiverse Averaging Procedure Implies a Graviton with Mass. Also Why a Single Repeating Universe Has No Massive Gravitons
In this chapter, we are looking at a generalization of Kolb and Turner’s [46] gravitational radiation result which is given as
![]() (49)
(49)
In the immediate aftermath of inflation, and just before inflation, we generalize ![]() as a constant,
as a constant,
as well as approximate ![]() as a constant, with also putting in [34]
as a constant, with also putting in [34]
![]() (50)
(50)
Then we have that if “Before” is just before the formation of the present universe, and “Final” is just after the formation of the present universe
![]() (51)
(51)
Claim 4, in the case of a single repeating Universe, the RHS of (51) is zero, leading to
![]() implying that the mass of a graviton in a single repeating universe is zero.
implying that the mass of a graviton in a single repeating universe is zero.
Proof: We will use the following value of the net energy, i.e. if ![]()
![]() (52)
(52)
Now define an average gravitational energy as given by having a single universe, denoted by N (fixed), i.e. one universe out of N of them [maybe infinite] given as
![]() (53)
(53)
This is the single universe, repeated, i.e. in this case, we assume that the Volume, per single repeating universe, is the same for a regime of the BB immediately before and after the cosmic explosion. Hence, we have that.
In terms of equipartition function definitions, and to rewrite Equation (52) as in the case of a multiverse, i.e. one out of N “universes”
![]() (54)
(54)
It so happens, then that there are r “states” per universe, and an infinite number of them. Then the average graviton radiation density would be, for r =1 to infinite number of energy states per Nth universe, with the label N (full-range) being the number of universe domains in a multiverse.
![]() (55)
(55)
In terms of the averaging procedure of Equation (42), we then have the initial and final states for the multiverse as
![]() (56)
(56)
![]() (57)
(57)
This would be due to the behavior of ![]() before the big bang, which will lead to
before the big bang, which will lead to
![]() (58)
(58)
Which should be compared to
![]() (59)
(59)
Equation (58) and Equation (59) above are not the same value, hence the results given in Equation (56). Hence the masses of the gravitons would not be the same by Equation (51).
Note that Feynman and Hibbs [47] have a different way of writing a net energy as can be written using ![]() as the total energy of the ith universe, and
as the total energy of the ith universe, and ![]() energy of the rth sub domain of the ith universe i.e. two different energy expressions.
energy of the rth sub domain of the ith universe i.e. two different energy expressions.
![]() (60)
(60)
Then, using Feynman and Hibbs [47] , the net energy can be written as
![]() (61)
(61)
The results as outlined above are, again then, more obvious.
13. Conclusions and Further Tests as Far as Upper Bounds to a Graviton Mass. with Consequences
First of all, the contributions of Gravitons to reacceleration of the universe are outlined as a consequence of massive gravitons. In addition, the graviton mass of a non zero value is central to the process of entropy generation which leads to our next comment which is a further research project in its own right. For what it is worth, we will address an extension of an entropy versus graviton production linkage implied in the first linkage. This entropy versus gravition linkage, as seen below, will imply a non zero initial radius for the universe. Before that is brought up, we should consider entropy generation with an initial cosmological “constant” (vacuum energy) at the start of inflation.
13.1. Difficulty in Visualizing What g* Is in the Initial Phases of Inflation
Secondly, we look for a way to link initial energy states, which may be pertinent to entropy, in a way which permits an increase in entropy from about 1010 at the start of the big bang to about 10100 today.
One such way to conflate entropy with an initial cosmological constant may be of some help, i.e. if
![]() or smaller, i.e. in between the threshold value, and the cube of Planck
or smaller, i.e. in between the threshold value, and the cube of Planck
length, We change the cosmological constant, as given by Padmabhan, with ![]() defined via Equation (62), in the referenced equation below as given by Padmanabhan [17]
defined via Equation (62), in the referenced equation below as given by Padmanabhan [17]
![]() (62)
(62)
Then make the following identification of total energy with entropy via looking at ![]() models, i.e. consider Park’s model of a cosmological “constant” parameter scaled via background temperature [48]
models, i.e. consider Park’s model of a cosmological “constant” parameter scaled via background temperature [48]
![]() (63)
(63)
A linkage between energy and entropy may be seen in the following construction, namely looking at what Kolb puts in [46] , i.e.
![]() (64)
(64)
Here, we in the following Equation (65) derive an explicit relationship between maximum initial cosmological vacuum energy and the initial entropy, of 1010, at the initial beginning of cosmological expansion
![]() (65)
(65)
Note that in the case that quantum effects become highly significant and that the contribution as given by
![]() and potentially much smaller, as in the threshold of Plancks length,
and potentially much smaller, as in the threshold of Plancks length,
going down to possibly as low as 4.22419 × 10−105 m3 = 4.22419 × 10−96 cm3 leads us to conclude that even with very high temperatures, as an input into the initial entropy, ![]() is very reasonable. Note that even if we have an initial non Zero entropy, Kolb and Turner still have the initial degrees of freedom
is very reasonable. Note that even if we have an initial non Zero entropy, Kolb and Turner still have the initial degrees of freedom ![]() as with an upper bound of 120, in contravention of exotic beyond the standard models with significantly higher initial degrees of freedom, whereas the author, in conversation with H. De La Vega, in 2009 [49] indicates that even the exotic theories of
as with an upper bound of 120, in contravention of exotic beyond the standard models with significantly higher initial degrees of freedom, whereas the author, in conversation with H. De La Vega, in 2009 [49] indicates that even the exotic theories of ![]() have an upper limit of about 1200, and that it is difficult to visualize what
have an upper limit of about 1200, and that it is difficult to visualize what ![]() is in the initial phases of inflation. De La Vega stated in Como Italy, that he, as a conservative cosmologist, viewed defining
is in the initial phases of inflation. De La Vega stated in Como Italy, that he, as a conservative cosmologist, viewed defining ![]() in the initial phases of inflation as impossible [49] . If the DM and DE contributions to
in the initial phases of inflation as impossible [49] . If the DM and DE contributions to ![]() are allowed, then this supposition as given by [49] is then drawn into question.
are allowed, then this supposition as given by [49] is then drawn into question.
One should not assume that the issue (does a non zero initial radii of the universe exist) is of decisive importance for the following, i.e. determining conditions for either supporting or denying the existence of non zero initial entropy, whereas we claim that non zero entropy is necessary in information exchange. How we break out of the alleged circular reasoning is to go back again to the datum of (48), namely we assert non zero initial entropy, to exchange information, in order to seek having the following hold from cycle to cycle.
The following will be what is to be worked upon, namely for now assuming that we can break down the degrees of freedom question as follows,
![]() (66)
(66)
The figure for the first entry is from Kolb and Turner, and what we assume we have to investigate is the bona fides of looking at what happens due to
![]() (67)
(67)
13.2. How the CMBR Permits, via Maximum Frequency, and Maximum Wave Amplitude Values, an Upper Bound Value for Massive Graviton Mass mg
Camp and Cornish (2004) [50] use the typical transverse gravitational gauge ![]() with a typically traceless value summed as
with a typically traceless value summed as ![]() and off diagonal elements of
and off diagonal elements of ![]() on each side of the diagnonal to mix with a value of
on each side of the diagnonal to mix with a value of
![]() (68)
(68)
This assumes r is the distance to the source of gravitational radiation, with the retarded designation on Equa-
tion (68) denoting ![]() replaced by a retarded time derivative
replaced by a retarded time derivative![]() , while TT means taking the trans-
, while TT means taking the trans-
verse projections and substracting the trace. Here, we call the quadrupole moment, with ![]() a density measurement. Now, the following value of the
a density measurement. Now, the following value of the ![]() as given gives a luminosity function L, where R is the “characteristic size” of a gravitational wave source. Note that if M is the mass of the gravitating system [50] .
as given gives a luminosity function L, where R is the “characteristic size” of a gravitational wave source. Note that if M is the mass of the gravitating system [50] .
![]() (69)
(69)
![]() (70)
(70)
After certain considerations reported by Camp and Cornish (2004), one can recover a net GW amplitude
![]() (71)
(71)
This last equation requires that ![]() º gravitational radius of a system, with a black hole resulting if one sets
º gravitational radius of a system, with a black hole resulting if one sets![]() . Note that when
. Note that when ![]() we are at an indeterminate boundary where one
we are at an indeterminate boundary where one
may pick our system as having black hole properties.
Now for stars, Camp and Cornish (2004) [50] give us that
![]() (72)
(72)
![]() (73)
(73)
As well as a mean time ![]() for half of gravitational wave potential energy to be radiated away as
for half of gravitational wave potential energy to be radiated away as
![]() (74)
(74)
The assumption we make is that if we model![]() , for a sufficiently well posed net mass M that
, for a sufficiently well posed net mass M that
the star formulas roughly hold for early universe conditions, provided that we can have a temperature T for
which we can use the approximation ![]() that we also have
that we also have ![]() or
or
higher, so that at a minimum we recover Grishchuck’s [51] value of
![]() (75)
(75)
Equation (75) places, for a specified value of R, which can be done experimentally, an upper bound as far as what a mass M would be. Can this be exploited to answer the question whether or not there is a minimum value for the Graviton mass? The key to the following discussion will be that
![]() (76)
(76)
13.3. Inter Relationship between Graviton Mass mg and the Problem of a Sufficient Number of Bits of ![]() from a Prior Multiverse Contribution to the Present Universe, to Preserve Continuity between Fundamental Constants Namely Planck’s Constant
from a Prior Multiverse Contribution to the Present Universe, to Preserve Continuity between Fundamental Constants Namely Planck’s Constant
P. Tinyakov (2006) [52] gives that there is, with regards to the halo of sub structures in the local Milky Way galaxy an amplitude factor for gravitational waves of
![]() (77)
(77)
If we use LISA values for the Pulsar Gravitational wave frequencies, this may mean that the massive graviton
is ruled out. On the other hand ![]() as proportional to the initial entropy leads to look-
as proportional to the initial entropy leads to look-
ing at, if
![]() (78)
(78)
If the radius is of the order of ![]() billion light-years ~ 4300 Mpc or much greater, then we have, as an example
billion light-years ~ 4300 Mpc or much greater, then we have, as an example
![]() (79)
(79)
![]() (80)
(80)
Equation (71) is in units where![]() .
.
If ![]() grams per graviton, and 1 electron volt is in rest mass, so
grams per graviton, and 1 electron volt is in rest mass, so ![]()
![]() . Then
. Then
![]() (81)
(81)
Then, there exist
![]() . (82)
. (82)
Conceivably this mass M would be transferred from a prior multiverse to a present universe, and may have been enough to preserve the value of Planck’s constant in the sense of what is represented in (48), as given above. This has much to do with the assumptions as given in [52] - [54] and should be experimentally tested as soon as possible. Particularly the value of Equation (81) is a counterpart to the values calculated in [54] , while different in absolute magnitude, the same procedure is in common between Equation (82) and reference [54] .
Of special note, is [55] , namely that gravitational waves have been discovered so that one can say with confidence, that LIGO.
Observed a transient gravitational-wave signal. The signal sweeps upwards in frequency from 35 to 250 Hz with a peak gravitational-wave strain of 1.0 × 10^―21. It matches the waveform predicted by general relativity.
Hence, we have a pretty good idea that at least the outward forms of General relativity have been experimentally vetted. This needs to be contrasted with [29] , in which if there are Gaussianity or non Gaussianity issues to contend with, as far as gravitational waves, that the data of [54] be vetted. In addition, the experimentally verified details as of reference [56] concerning two black holes generating Gravitational waves have crucial experimental detail. The reference [56] has the following quote
We constrain the graviton Compton wavelength in a hypothetical theory of gravity in which the graviton is massive and place a 90%-confidence lower bound of 10^13 km. Within our statistical uncertainties, we find no evidence for violations of general relativity in the genuinely strong-field regime of gravity.
i.e. General relativity appears to hold up well, but in terms of configuring admissible values of a massive graviton, as alluded to in this document, it would be appropriate to review data as to the presumed Compton wavelength of a “massive graviton” and to insure that it is commensurate with Section 13.3 above. i.e. we view that it is, but that in the future we should make the great refinements outlined as given in Section 13.3 which should be adhered to, once the procedures of [56] are refined via additional experimentation.
Finally, and not least is, that the ultimate goal should be to determine the utility of not only [56] but of [57] , i.e. to determine if scalar-tensor gravity, which would be commensurate with 3, instead of 2 polarization states for gravitation, or classical General relativity is favored by the data. Correct review of [55] and [56] plus refinements of Section 13.3 will hopefully allow researchers to determine this, and it would be through utilization of
accurate angular and frequency dependent response functions of interferometers for GWs arising from various Theories of Gravity, i.e. General Relativity and Extended Theories of Gravity, will be the definitive test for General Relativity.
The good news is that we are through [55] and [56] learning enough so as to make this determination, and it has to do with refinement of enough information to look at frequency response functions, which was a particular focal point of [55] as to their very careful LIGO work.
In doing all of this it is useful to keep in mind that [55] to [57] plus review of Section 13.3 above will permit the following, namely as was stressed in an interaction the author had with the editors of this journal, that
the realization of gravitational wave astronomy will be important for discriminating among general relativity and other gravity theories
Finally what we will be doing through reference [58] is to take the analogy of instaton-anti instaton nucleation given in Figure 2 above a step further. What we obtain is possibly a way to link SO (4) theory and symmetry breaking to an alternative to the usual Higgs boson formation of mass, assuming that the Graviton has a slight mass. This requires serious analytical work and will be followed up in future publications. It likely entails further developments linking reference [58] to reference [59] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.