On the Concept of Circle and Angle in Galilean Plane

Abdullah Kurudirek, Hüseyin Akça

Eğitim Fakültesi Matematik Bölümü, Işık üniversitesi, Erbil, Irak.

DOI: 10.4236/oalib.1101256                

Abstract

In this paper, we try to show what some basic definitions like angle and circle which are taught in Euclidean plane at secondary and high schools, mean in Galilean plane. Furthermore we try and target to introduce the results of angle and circle concepts, comparing different situations of the same definitions in Galilean and Euclidean planes.

Keywords

Galilean Plane, Special Lines, Negative Angle, Parabolic Measure, Circle, Cycle

Subject Areas: Geometry, Mathematical Analysis

1. Giriş

Bilindiği gibi, Galileo düzleminde alınan herhangi ve noktaları arasındaki mesafe 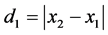eşitliği ile tanımlanıyordu. olduğu durumda ise, mesafe 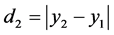eşitliği ile

tanımlanmaktaydı [1] . Eğer noktalar oy-koordinat eksenine parallel doğrular üzerinde olursa aralarındaki mesafe ikinci eşitlik ile hesaplanır. Bundandolayı, oy-koordinat eksenine paralel doğrulara özel doğrular adı verilir [2] .

2. Bulgular

Şimdi, iki nokta arasındaki mesafe kavramından ve çemberin Öklid düzlemindeki tanımından faydalanarak Galileo düzleminde çemberi tanımlayabiliriz.

Tanım: Galileo düzleminde, verilen herhangi bir noktaya eşit mesafede bulunan noktaların geometrik yerine

çember denir. Eğer 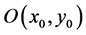çemberin merkezi, r çemberin yarıçapı ve çember üzerinde herhangi

bir nokta olsa bu çemberin denklemi,

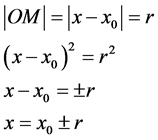
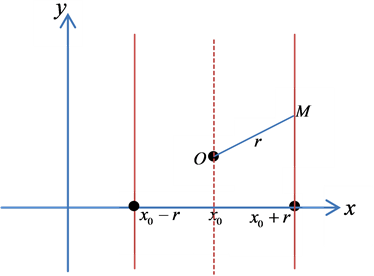
eşitliği ile ifade edilir.

Çemberin merkezi orijinde olursa o zaman çemberin denklemi olur ve burada çemberin merkezi de özel doğru noktalarından oluşur. O halde, Galileo düzlemindeki çemberin iki özel doğrudan oluştuğunu söyleyebiliriz [3] .

Galileo düzlemindeki açı kavramı da yine Öklid düzleminde kikavramlardan yararlanılarak tanımlanır. Açının ölçüsü olarak; merkezi, açı ucunda olan çember yayının uzunluğu alınır [4] .

Eğer ve 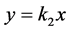doğruları, köşesiorijinde bulunan açının kenarları olursa bu açının ölçüsüile hesaplanır.

Galileo düzlemindeki açı arasında olup, buna açının parabolik ölçümü denir. Galileo düzlemindeki açı kavramını verme ve onun Öklid anlamındaki açı kavramı ile karşılaştırılmasını yapma fikri, okullarda normal geometri ders saatlerinin haricinde ki zamanlarda verilebilecek konulardır. Açı kavramınınher iki durumda verilebileceğinin mümkün olduğunu gösterdiği gibi aynı zamanda açı ölçüsünün sınırlandırılamayışı hakkında da malumat vermektedir.

ox-yatay ve oy-dikey koordinat eksenleri boyunca alınan dar açının parabolik anlamda ölçümü ve onların büyüklüklerinin kıyaslaması pratikde oldukça kolaydır.Burada açıyı, açıölçer yardımıyla ölçerken, açı ölçerin sade ve iyi tanımlanmasından dolayı hesaplamanın çok kolay olduğu görülür.

Galileo düzleminde açı kavramının kendisine aitgeniş özellikleri vardır. Mesela özel doğru, açının kenarları arasında olduğunda Galileo düzlemi, çemberi onun iki kenarını kesememektedir. Bu durumda açı kenarlarından birinindevam ettirilerek çember yayı ile kesişmesinden faydalanılır.

Burada elde edilen dış açı, verilen açı ölçüsü şeklinde alınır ve bazı durumlarda bu negatif açı olarak da hesaplanır. Ayrıca, doğal olarak Galileo düzleminde dar açı, dik açı ve geniş açı düşüncelerinden bahsedemeyiz.

Galileo düzleminde açı kavramı aşağıdaki özelliklere sahiptir.

1) Dikaçılar birbirlerine denktir.

2) Komşu açılar denk ve zıt işaretlidir, yani komşu açıların toplamı sıfırdır,.

3) Ortak kenara sahip iki açının toplamı aşağıdaki gibi ifade edilir.

4) Kenarları paralel olan açıların ölçümleri mutlak değerlerine denktir.

Öklid düzlemindeki paralel iki doğruyu kesen başka bir doğruyla meydana gelen açıların kendi arasındaki denkliklerini yada mutlak değerce denkliğinin ispatını göstermek öğrenciler için ilginç bir ödev konusu olabilir. Bilindiği gibi, Öklid geometrisindeki çember; “Verilen herhangi bir AB doğru parçası, her bir noktasından aynı açı altında görünen noktaların geometrik yeri” şeklinde de ele alınarak tanımlanabilir.

Şimdi, Galileo düzleminde bu özelliğe sahip olan noktaların geometrik yerine bakalım.

Теоrem: Galileo düzleminde verilen AB doğru parçasının her bir noktasından aynı açı altında görülen noktaların geometrik yeri bir paraboldür. Burada parabolün simetri ekseni özel doğrudur.

İspat: ve verilen AB doğru parçasının uç noktaları olsun. noktasından AB doğru parçasına h açısıylaşekildeki gibi CA ve CB doğruları arasındaki açı aynı h açısına denktir. Bunu göstermek için CA ve CB doğrularının denklemlerini bulup onlar arasındaki açıyı h’yeeşitleyelim.

Verilen iki noktadan geçen doğru denklem formülünü kullanarak;

denklemlerini yazabiliriz. Ayrıca bu doğruların eğimlerini sırasıyla

ile gösterecek olursak, olduğunu da göz önünde bulundurarak;

elde edilir.

Gerekli cebirsel işlemler yapıldığında,

bulunur.

Buradan da katsayıları,

şeklinde seçersek

deklemi elde edilir ki buda bir paraboldür.

Gerçekten de bu denklem noktaları, simetri ekseni özel doğruda olan parabole ait olduğunu ve olduğunda doğru parçasının ox-koordinat eksenine paralel olmadığını gösterir. Yani, bu incelenen doğru parçası özel doğru üzerinde değildir. Çemberin bu tanımını veren noktaların geometrik yerine cycle denir [4] . Buradan, Galileo düzleminde Öklid düzleminin çemberine aitözelliklerin olduğu doğrunun, parabol (cycle) olduğu sonucu çıkar.

Yine bilindiği gibi, Galileo düzlemindeki hareket denklemi ile ve koordinat eksenlerini h açısına döndürme ise ile tanımlanır [2] .

3. Sonuç ve Tartışma

Öklid düzleminde merkezi orjinde bulunan çember, koordinat düzlemini döndürüldükçe çember üzerindeki noktalar çember boyunca yerleşir, ama şekil değiştirmez. Galileo düzlemindeki cycle’ında bu özelliğe sahip olduğu gösterilebilir. Bu durumöğrenciler için düzlemi kendi içinde bir birimlik döndürüş özelliklerini öğrenmek için ödev olarak bırakılabilinir.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Artıkbayev, A., Kurudirek, A. and Akça, H. (2013) Occurrence of Galilean Geometry. Applied and Computational Mathematics, 2, 115-117.
[2]	Артыкбаев, А. and Соколов, Д.Д. (1991) Геометрия в целом в плоском пространстве-времени. Ташкент. Изд. «Фан».
[3]	Kurudirek, A., Akça, H. and Erdoğan, M. (2013) On Geometries in Affine Plane. Applied and Computational Mathematics, 2, 127-129. http://dx.doi.org/10.11648/j.acm.20130206.13
[4]	Yaglom, I.M. (1979) A Simple Non-Euclidean Geometry and Its Physical Basis. Springer-Verlag, New York.