Light and Entanglement Velocities for the Electron and the Proton in Minkowskian Space Require Surface Areas that Approximate the Human Cerebrum: Implications for Excess Correlations ()
Received 23 May 2016; accepted 24 June 2016; published 29 June 2016

1. Introduction
The concept of excess correlation between processes or events separated by distances that would exhibit a low probability of involving causality requires candidates for its manifestation. Causality implicitly assumes that the concordance of responding between phenomena occupying two loci occurs because of a serial mediator that can be measured or potentially measured. An upper limit to this diffusivity, such as the velocity of light in a vacuum, is assumed. Concordance can be defined as a significant correlation of the fluctuations of a shared property as a function of serial time whose increments (Δts) can be simultaneous or displaced. In most models the correlations approach 1.0 when causality is assumed. The serial mediator for causal events usually presumes a medium or process within the medium that permits the concordance. Historically these have ranged from the 19th century ether to the contemporary forms of permittivity and permeability of “space” and more recently macro-space manifestations of zero point vacuum oscillations [1] . Mediums determine boundaries. For example, the square root of the ratio of μ0 (permeability) to ε0 (permittivity) is the impedance (in ohms) of free space.
Causality is remarkably circumscribed by the locality. It is associated with small increments of space (Δs) and time (Δt). The progression through these serial increments involves energy to compensate the intrinsic impedance associated with traversing multiple proximal boundaries (Δs, Δt) within the medium. Within modern descriptions these boundaries are defined as properties of space that include impedance and capacitance. Consequently for processes such as forces that are mediated through causal and local phenomena the magnitude of the change in property that will contribute to the concordance with another phenomena usually decreases, most frequently as the inverse square, as a function of distance. The time with which this change can occur is also circumscribed. In general this is reflected as a relationship between order of magnitude for space and time [2] . For example, femtometer space (the level of the proton and electron) phenomena are optimally discernable with femtosecond time. Millimeter space phenomena (the level of the neuron) are optimally discernable with millisecond time. For processes to be discerned there must be at least two successive increments (2∙Δt).
On the other hand phenomena associated with non-locality display excess correlations that are not attenuated by distance and could occur anywhere within space or time. Traditionally it is assumed to be “instantaneous” although some quantitative value would not necessarily be excluded given that a non-zero value is always a probability. One explanation for this capacity is that non-local phenomena are coupled to the property of the entire set: the universe. Because it displays one ΔS and one ΔT, there can be no 2∙ΔT and hence no processes. As a result there is no “time” in the traditional sense. Some phenomena, such as photons, at the level of the total universal set would be timeless. Any event or process that shares this condition could respond, as manifested by excess correlation, to another homogeneous event or process anywhere with the space-time continuum of the total set (the universe). This concept is a more quantitative variant of the brilliant work of Sheldrake [3] .
This condition would allow quantum energy teleportation without a limit of distance [4] . The connection could occur anywhere within time because the properties diverge from the total age of the universe or just before it emerged as a single set as described by Hu and Wu [5] . Consequently, all components of the universe contain a subset of that initial state. One interpretation of this distinction for non-locality which involves a direct relationship to the entire set (ΔS, ΔT) and locality which is circumscribed in space-time increments is that causality is a subset of excess correlation (rather than a primary operator) that emerges or is apparent when the Δs, Δt is  ΔS ΔT. If locality is strongly related with diffusivities between loci that are bounded by the velocity of light, then non-locality must be associated with a second indicator of diffusivity that accommodates the much larger magnitude associated with the total set and the perception of “instantaneous” in order to accommodate the theoretical example of the “simultaneous” shift in the parity of one photon when its entangled photon’s parity is reversed.
ΔS ΔT. If locality is strongly related with diffusivities between loci that are bounded by the velocity of light, then non-locality must be associated with a second indicator of diffusivity that accommodates the much larger magnitude associated with the total set and the perception of “instantaneous” in order to accommodate the theoretical example of the “simultaneous” shift in the parity of one photon when its entangled photon’s parity is reversed.
2. Locality and Non-Locality Solve for Two Velocities in Minkowksi Space
Persinger [6] has suggested that the temporal solution for Gσ where G is the gravitational constant (6.67 × 10−11 m3∙kg−1∙s−2) and σ is the average density of matter in the current universe assuming a base unit particle, the proton (1.67 × 10−27 kg∙m−3). The upper boundary for the final epoch is about 2.996 × 1018 s or about 95 billion years. Similar values have been derived from different approaches as described by Hoffman et al. [7] for the final epoch. This suggests that the present duration of the universe is only about 13% - 15% of its totality. The proportion is very similar to the estimated values of baryons or regular matter. From this perspective the discrepancies in measurements that have been attributed to dark matter and energy would be matter and energy yet to occur. Its virtual presence suggests that there is some unifying variable that allows connection throughout the space-time manifold.
For entanglement to occur the events or processes would be required to share the properties of homogeneity and pervasiveness within the total set, the universe. Two traditional candidate particles would be the electron and proton. Although subatomic particles are important phenomena that indicate the potential constituents of the proton and electron, their properties (singly and when in aggregates) define the characteristics of elements and compounds that are the behaviour of matter. In previous calculations we [8] have indicated the possibility that the Compton wavelengths of the proton and electron are bifurcations of potentially a single source related by a fundamental geometry that describes the spatial structure of the universe. There are many potential geometric possibilities that could define essential space within the universe. One of them is 21.3π4 [9] which is the resultant constant of the product of the four dimensional representations of symmetrical closed boundaries. Application of this value allows rational estimates for the recondite energies of magnetic and electric fields represented within space but not as yet expressed [10] .
The metric for these four dimensions was described by Minkowski [11] as the square root of four indicators:
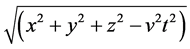 . Petkov [12] has discussed the possibility that Minkowski space is represented in reality
. Petkov [12] has discussed the possibility that Minkowski space is represented in reality
at the macroscopic level. The operation of a square root produces two implicit solutions (±) and an additional condition (imaginary, i) if the square root is obtained from a negative value. Presumably the transition point where the solution is the smallest value within the limit approaching 0 but positive is an interface of some type. In Minkowski’s original formulation v2 was set equal to c2 or the square of the velocity of light in a vacuum. When only the complex term v2t2 is considered the value required to reduce v2 to an identity (unity) is the duration whose frequency is 3 × 108 Hz. This is about 21% of the value for the neutral hydrogen line (1.42 × 109 Hz).
Hence only very small values in each of the three spatial planes would be sufficient for the square root of the entire equation to be > 0. The hydrogen line is primarily a single electron phenomenon as it orbits the proton. The energy associated with this wavelength is determined by the hyperfine changes in the 1 s orbit due to slight alterations in the interactions between rotational (spin) magnetic moments of the proton and electron. Once every approximately 10 million years the electron dipole shifts and this small discrepancy between the spin parallel or antiparallel with the direction of the orbit contributes to the energy that produces the 21 cm wavelength. Because the mass of the universe is approximately 90% hydrogen this wavelength will be ubiquitous within the volume.
Several theoretical astrophysicists have suggested that non-local phenomena are “instantaneous” [13] [14] . Most approaches assume a central role of non-local gravity and that this process is not limited to the velocity of light transfer. Hence there are no “gravity waves” in the traditional sense because gravity is nonlocal and instantaneous. Waves imply time and the amplitude changes over time could be considered a component of the effect of traversing successive boundaries that compose the structure of the medium. Quantum physicists who describe gravity from this perspective have employed the “jiffy” as a unit. It is the time required for the velocity of light to traverse the radius of an electron, or about 0.94 × 10−23 s. If the radius of an electron is coupled to its orbital velocity and the shift in spin associated with hydrogen line then this metric becomes illustrative. The equivalent distant covered within 2πλ where λ = 21.1 cm per jiffy would be equivalent to 1.41 × 1023 m∙s−1.
Persinger and Koren [15] have been pursuing the entanglement concept and the velocity of its diffusivity at the level of the entire universal set. Two different approaches indicated a value of ~1023 m∙s−1. The first was found when the product of the geometries 2πr, 4πr2 4/3πr3 and 2πrf was obtained (21.3π4 m7∙s−1) and set equal to the parsimonious dimensional equivalent that reflected G, and the mass (m), length (d) and duration (t) of the universe as now estimated. The optimal combination to balance the equation was 21.3π4f = G2∙m2∙d∙t3. When typical average values were substituted for the mass, length and duration, the result of the 7th root was 2.84 × 1023 m∙s−1. With the second approach the total energy within the universe, based upon an assumed mass of 2.38 × 1052 kg was 2.14 × 1069 Joules and when the equivalent electric field gradient was divided by the magnetic field strength [16] associated with this energy, the velocity term was ~1 × 1023 m∙s−1. The latter coefficient approached the first solution if the volume of the universe was assumed to be its value during the final epoch.
These two procedures that involved the entire universal set indicated the presence of an intrinsic velocity of ~1023 m∙s−1. The equivalent velocity involving the quantum jiffy when applied across the hydrogen line, which is proliferated within the universe, is also 1.23 × 1023 m∙s−1. Consequently the value is reflected at the micro-spatial level where matter emerges and at the total value, the universal set, where matter and energy become indistinguishable during the final epoch. The equivalent frequency required to converge to an identity for v2t2 or (2.84 × 1023 m・s−1)2 is 0.35 × 10−23 or 2.85 × 1023 Hz. The equivalent energy (when multiplied by Planck’s constant) is 18.88 × 10−11 J. The energy equivalence of the mass of a proton is 15.03 × 10−11 J. Consequently the “entanglement” related energy within Minkowski space is about 25% of the energy equivalence of the mass of a proton.
In other words, the two values for “v”, c (the velocity of light) and Ψ (the entanglement velocity) for the component of the Minkowski space, involve the temporal component required for energies that approach that which are relevant to the electron and the proton. The discrepancy from the exact value that would be equivalent to the energy associated with the hydrogen line and with the energy of a proton would require relatively small values for the three planes of space for the solution of the equation to be > 0. We have assumed this interface is a threshold for the emergence of entanglement. The exact values for three-dimensional space to produce this condition (>0) could be revealing.
3. The Ranges of Dimensions of the Human Cerebrum Accommodate the Residual Spatial Requirements
For the solution of 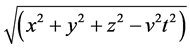 to be > 0 when v = c, the velocity of light, the aggregate −c2t2 would
to be > 0 when v = c, the velocity of light, the aggregate −c2t2 would
be a value that is > 4.46 × 10−2 m2 which is the product of c2 and the squared duration for the neutral hydrogen line frequency. Assuming the distances were equal for the three planes, x, y, and z, then the areas of each plane would be 1.49 × 10−2 m2 or a width of ~12.2 cm. This is within the range of volumetric values for the human cerebrum. According to the Blinkov-Glezer data [17] the actual x, y, z would be: length: 15.5 to 19. 0 cm, width 13.1 to 14.1 cm, and height: 10.8 to 11.7 cm.
The mean values for the diameter of each plane: 1.72 × 10−1 m, 1.36 × 10−1 m, 1.13 × 10−1 m and the volume, assuming an ellipsoid, would be 1380 cc which is a typical median volume for the human cerebrum. The radius would be 6.91 cm. Clearly the range around this centroid would be considerable. However a significant portion of all human brains’ three dimensional metrics would contain the values that would allow the hyperspace solution for the proton and the electron to be non-imaginary. Hence actual real ranges of the surface area of the cerebrum of the human brain would overlap with the threshold for the connection between hyperspace involving the hydrogen line and velocity of light. The cerebral dimensions would be distributed within a subpopulation of human beings who would be particularly resonant with the limen of > 0.
For the solution of 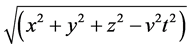 to be > 0 when v = Ψ, the entanglement velocity is considered a
to be > 0 when v = Ψ, the entanglement velocity is considered a
convergence. Because of the greater exactness of the “jiffy” and the inclusion of the neutral hydrogen wavelength in the numerator, the value 1.41 × 1023 m∙s−1 (1.98 × 1046 m2∙s−2) was assumed. Because entanglement and excess correlation are assumed to be mediated by the proton, the duration of its frequency equivalence was employed for t2. The energy of the mass equivalence for a proton is 15.03 × 10−11 J and when divided by Planck’s constant is 2.27 × 1023 Hz. The inverse is 0.44 × 1023 s or 0.19 × 10−46 s2.
The product of the squared entanglement velocity and duration equivalent of the energetic frequency of the proton is −0.376 m2. This means that a combination of spatial values within 3-D space must be at least equal to this value to approach zero and avoid an imaginary value. The cerebral cortical surface area ranges from 0.147 to 0.167 m2 according to several authors [18] . However, since two-thirds of the surface areas are contained within sulci and gyri, the total surface area folded within the surface volume would allow a value that would approach the threshold.
4. The Decay of Superimposed States with Self-Energy Equal to the Energy of an Action Potential
Just as spatial parameters of the human cerebrum satisfy values which approach threshold conditions for Minkowski solutions involving the hydrogen line and entanglement velocity, energies intrinsic to the brain could accommodate superposition of mass-equivalent neural states. Penrose [19] explains that a macroscopic quantum superposition of paired mass distributions is fundamentally unstable, where the lifetime T describes the temporal increment of decay and dissociation. It was suggested that T was approximately equal to the quotient of Planck’s constant (dividend) and the gravitational self-energy (divisor) of the system:
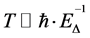 (1)
(1)
where ħ is reduced Planck’s constant (1.05 × 10−34 J∙s) and E∆ is the gravitational self-energy of the difference between the mass distributions of the two superposed states. The energy value of 2 × 10−20 J has been described as a fundamental unit which is conserved across the nervous system from the level of the whole brain to the cell membrane and biomolecular pathways which transduce cell-to-cell signals [20] . Solving for T, the temporal increment involved in the decay of supposed states would be 5 × 10−15 seconds if E∆ is equal to 2 × 10−20 J. This is the approximate time required for a photon travelling at c or 3 × 108 m∙s−1 to traverse the typical width of a neuron or ~5 - 10 µm. That is to say, the decay rate of superimposed mass distributions with equivalent self- energies approximating those which are involved with the action potential and the maintenance of the membrane electric potential difference (V) is equivalent to the time required for light to pass through a neuron or an equivalent micrometer-range spatial increment.
5. The Hydronium Proton within Brain Water as a Potential Mediator of Entanglement
Cognition is associated with the production of temporally-patterned action potentials. When the consequences of these temporal patterns are disrupted, such as the simultaneous release of neurotransmitters devoid of the corresponding temporal structure subsequent to a critical force to the skull, “unconsciousness” occurs. Each action potential is associated with a net change of about 1.2 × 10−1 V. If this potential difference was applied across the Compton wavelength of an electron (2.42 × 10−12 m) the equivalent voltage would be 0.5 × 1011 V∙m−1. When this value is divided by the estimated strength of the dynamic magnetic field associated with action potentials (0.5 × 10−12 T) as measured by magnetoencephalography [21] , the velocity term is ~1023 m・s−1. This velocity would be associated with the energy within Minkowski hyperspace for the proton that can be simulated when the action potential shift in voltage is represented within the space occupied by the electron’s energetic (Compton) wavelength.
The relationship between the energy associated with the Compton wavelength for the electron and the neutral hydrogen line that determines the first solution for the Minkowski hyperspace > 0 should be coupled to a universal property with which entanglement is associated. The energy associated with the mass equivalent of an electron is 8.1 × 10−14 J while the energy associated with the hydrogen line is 9.4 × 10−25 J. For the two to converge the neutral hydrogen line must have an intrinsic oscillation of 0.86 × 1011 Hz. This frequency when multiplied by Planck’s constant (6.626 × 10−34 J・s) results in an increment of energy that is 5.7 × 10−23 J. From the Boltzmann equation this energy would be reflected as 4.1 °K. This is within error of measurement of the Cosmic Microwave Background (2.72 °K) which has been suggested as the source of the limited duration of entanglement between proton energies in pH reactions in physiological-simulated water within our experiments involving weak rotating magnetic fields [22] .
The importance of 10−12 T magnetic fields is expressed from several perspectives. First the typical potential difference from quantitative electroencephalographic (QEEG) measurements of the cerebrum during cognition (40 Hz) is about 2 μV. When divided by the resistivity of the extracellular fluid of 2 Ω∙m the current gradient is 10−6 A∙m−1 and when multiplied by the average length of the cerebrum, the current is 10−7 A. When this value is divided by the inverse of the intrinsic diffusivity (Ω・m multiplied by magnetic permeability) the resulting magnetic field flux density is 10−12 T. This magnitude has been strongly correlated with fundamental cerebral functions during the conditions that are associated with consciousness and cognition. This is also the intensity of the Schumann Resonance magnetic field component within which human brains are immersed. These frequencies display harmonics from the fundamental (7 - 8 Hz) with increasing increments of about 6 Hz through 13 - 14 Hz, 19 - 20 Hz, etc. [23] . Saroka and Persinger [24] have measured manifestations of the Schumann Resonances within the spectral power densities of normal human quantitative electroencephalographic measurements.
The process within the cerebrum at the level of the membrane that results in the creation of pT magnetic fields should involve the proton if it is involved with entanglement. There are between 100 and 1000 more water or proton channels with the plasma cell membrane of cells than all of other types of channels combined [25] . The magnetic field generated within a channel, assuming it is the shape of a cylinder, can be estimated by:
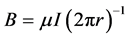 (2)
(2)
where I is the current and μ is magnetic susceptibility. The estimated current for a proton channel is pH dependent [25] . Within the range of pH found adjacent to the plasma cell membrane of the neuron the current is 10−15 A (femtoAmp). Assuming the width of the channel is 1 nm, then the magnetic field strength would be 10−12 T. If these values generated by a specific pH of proton channels were coupled to the similar intensity that defines the cerebral cortical field while it is immersed in galactic fields, then the potential for access to the geometry associated with Minkowski hyperspace and entanglement would be increased.
This magnetic field intensity may also be relevant to the temporal duration of the effect. A component of entanglement is that once it occurs it could be manifested anywhere within the space and time of the total unit. The change in angular momentum from an applied magnetic field can be described as:
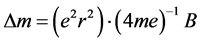 (3)
(3)
where e is the unit charge, r is the Bohr radius for the electron, me is the mass of the electron and B is the strength of the applied magnetic field. If the applied magnetic field strength is 10−12 T, the magnetic moment is 10−40 A∙m2. If this magnetic dipole moment is immersed within the galactic universal fields then the energy is 10−52 J [26] . When divided by Planck’s constant (6.626 × 10−34 J∙s), the resulting duration is within the range of 1018 s. This is the order of magnitude of the age of the universe.
6. Conclusion
Recent experiments have indicated that excess correlation between specific types of brain activity occurred between human subjects separated by thousands of kilometers while they shared very specific components of applied circum cerebral magnetic fields with specific rates of angular velocity. The effect was optimal when the product of the proton’s magnetic moment and portions of the applied field would have matched the energy whose quantum frequency was congruent with the rate of rotation. The capacity for this type of entanglement to involve much larger areas of space-time and to be mediated by a velocity much faster than light is suggested by the solution of the proton’s mass when the frequency associated with this “entanglement velocity” is applied within Minkowskian geometry. Only when the three spatial planes are at quantities that produce a greater square root value than zero would the solution be non-imaginary. The velocities of light in a vacuum and the hypothetical “diffusivity” associated with excess correlation (entanglement) solve for energies with equivalent masses coupled to the electron and proton. The discrete dimensions for these planes required for a non-negative (non- imaginary) solution traverse the range of volumes of the human cerebrum.