Received 5 May 2016; accepted 24 June 2016; published 27 June 2016

1. Introduction
Electron spin relaxation in semiconductors has attracted considerable attention because of its essential role in the application of spintronic devices [1] - [3] . Important electron spin relaxation mechanisms include the Elliot-Yafet (EY) [4] [5] and “Dyakonov-Perel” (DP) [6] mechanisms. For larger gap materials, the DP mechanism has been shown to dominate the spin relaxation at high temperatures [7] - [10] , whereas Dzhioev et al. [11] report that the dependence of the spin-relaxation rate on the electron mobility in lightly doped n-GaAs bulk crystals disagrees with the results predicted by the DP mechanism. They attribute the spin relaxation to the electron-electron interaction. Many studies have examined the temperature and magnetic field dependence of the spin relaxation time [11] - [15] , whereas the dependence of the spin relaxation time on the carrier concentration has received relatively little attention [9] [16] . Murdin et al. [16] show that the carrier density dependence of the spin lifetime in InAs is reversed at  and suggest that electron-electron interaction affects the dependence of the spin lifetime on the carrier concentration.
and suggest that electron-electron interaction affects the dependence of the spin lifetime on the carrier concentration.
This study calculates the electron density dependence of the electron spin relaxation time in a system of electrons interacting with piezoelectric acoustic and polar optical phonons through phonon-modulated spin-orbit coupling using the formula for the electron spin resonance obtained using the Kang-Choiprojection-Reduction (KCPR) method [17] . In spintronics, preserving the information injected into spin over a practical timescale is important for spintronics devices. Therefore, it is important to understand how the Planck distribution function for phonons and the Fermi distribution function for electrons are included in the spin relaxation time because the density and temperature dependence of the spin relaxation time are caused by the distribution functions. The formula used in this paper includes two distribution functions in multiplicative forms (not in simple additive forms), which is physically acceptable because electrons and phonons belong to different categories in a quantum-statistical classification. Therefore, the absorption and emission processes of phonons and photons in all electron transition processes can be explained in an organized manner, and the spin flipping and conserving processes can be interpreted from a fully microscopic point of view [18] .
This paper investigates the effects of piezoelectric acoustic and optical phonon scatterings on the electron spin relaxation. For that purpose, the electron density and temperature dependence of the spin relaxation time in GaAs are calculated and the results are discussed by a comparison with the experimental data.
2. Review of Theory
An electron transferred from a spin down state with a lower energy to a spin up state with a higher energy by absorbing electromagnetic radiation must return to the spin down state by an interaction with the background. This process is characterized by the electron spin relaxation time,  , which is related to the line shape function,
, which is related to the line shape function, 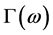 , where
, where  is the angular frequency of the electromagnetic wave, as
is the angular frequency of the electromagnetic wave, as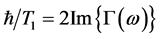 , where it means “the imaginary part of”.
, where it means “the imaginary part of”. 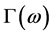 is contained in the electron spin resonance formula.
is contained in the electron spin resonance formula.
The electron spin relaxation time in a system of electrons interacting with phonons through phonon-modu- lated spin-orbit coupling is expressed as [17] [18]
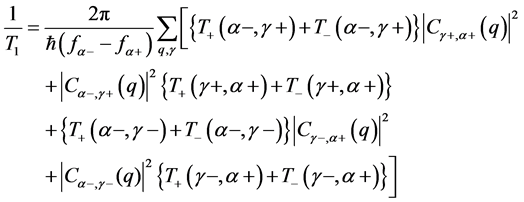 (1)
(1)
Here 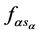 is the Fermi distribution function for an electron with energy
is the Fermi distribution function for an electron with energy  and spin
and spin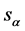 ,
, 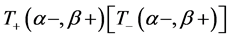 means the clockwise (counterclockwise) spin flipping process between the states,
means the clockwise (counterclockwise) spin flipping process between the states,  and
and , and
, and 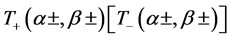 is the clockwise (counterclockwise) spin conserving process between the states,
is the clockwise (counterclockwise) spin conserving process between the states,  and
and ![]() [17] . The energy eigenvalue under a static magnetic field, B, applied along the z-axis can be written as
[17] . The energy eigenvalue under a static magnetic field, B, applied along the z-axis can be written as
![]() (2)
(2)
where![]() ,
, ![]() is the cyclotron frequency,
is the cyclotron frequency, ![]() is the z-component of the electron wave vector, g is the electron g-factor,
is the z-component of the electron wave vector, g is the electron g-factor, ![]() is the Bohr magneton,
is the Bohr magneton, ![]() for an up (down) spin, and
for an up (down) spin, and ![]() (
(![]() ) is the transverse (longitudinal) effective mass. In Equation (1), the electron-phonon coupling factor,
) is the transverse (longitudinal) effective mass. In Equation (1), the electron-phonon coupling factor, ![]() , is given as [4] [5]
, is given as [4] [5]
![]() (3)
(3)
where ![]() is the effective mass of an electron, c is the speed of the light,
is the effective mass of an electron, c is the speed of the light, ![]() is the momentum operator of an electron,
is the momentum operator of an electron, ![]() is the vector potential,
is the vector potential, ![]() is the Pauli spin matrix, and
is the Pauli spin matrix, and ![]() is the electron-phonon interaction potential that depends on the mode of the phonons.
is the electron-phonon interaction potential that depends on the mode of the phonons.
The first two terms in Equation (1) can be interpreted as follows: ![]() means an implicit spin flipping process between an initial spin down state (
means an implicit spin flipping process between an initial spin down state (![]() ) and an implicit spin upstate (
) and an implicit spin upstate (![]() ). Photon absorption or emission processes and phonon absorption or emission processes are included in
). Photon absorption or emission processes and phonon absorption or emission processes are included in ![]() (Figure 1(a)) corresponds to
(Figure 1(a)) corresponds to![]() . These processes form loops because the phonon absorption process maintains balance with the emission process.
. These processes form loops because the phonon absorption process maintains balance with the emission process.![]() , which is denoted by a blue (right) spring in Figure 1(a), means that an implicit spin up state is induced from a final spin up state (
, which is denoted by a blue (right) spring in Figure 1(a), means that an implicit spin up state is induced from a final spin up state (![]() ) by an electron-phonon interaction. The implicit spin up state and down state (
) by an electron-phonon interaction. The implicit spin up state and down state (![]() ) are thus named because they are included only in the relaxation time, not in the electron spin resonance formula. The second two terms correspond to the spin conserving processes, i.e.,
) are thus named because they are included only in the relaxation time, not in the electron spin resonance formula. The second two terms correspond to the spin conserving processes, i.e., ![]() means an implicit spin conserving process between an implicit spin up state and a final spin up state, and
means an implicit spin conserving process between an implicit spin up state and a final spin up state, and ![]() means that the implicit spin up state is induced from the initial spin down state (Figure 1(b)) corresponds to
means that the implicit spin up state is induced from the initial spin down state (Figure 1(b)) corresponds to![]() . The other four terms in Equation (1) can be interpreted in a similar manner [18] .
. The other four terms in Equation (1) can be interpreted in a similar manner [18] .
3. Numerical Results
Piezoelectric acoustic and polar optical phonon interactions are the dominant scattering mechanisms at high temperatures in III-V compounds. The acoustic strain induced by pressure in a crystal whose lattice lacks inversion symmetry gives rise to a macroscopic electric field, which is assumed to be proportional to the derivative of the atomic displacement, ![]() , where
, where ![]() is the mass density,
is the mass density, ![]() is the volume of the system,
is the volume of the system, ![]() is the polarization vector, and
is the polarization vector, and ![]() is the annihilation (creation) operator for a phonon with energy
is the annihilation (creation) operator for a phonon with energy![]() . In contrast,
. In contrast, ![]() is proportional to the polarization for the optical mode because the electric displacement is proportional to the polarization. Then, Equation (3) can be expressed as follows:
is proportional to the polarization for the optical mode because the electric displacement is proportional to the polarization. Then, Equation (3) can be expressed as follows:
![]() (4)
(4)
Here, ![]() for polar optical phonon scattering and
for polar optical phonon scattering and ![]() for piezoelectric phonon scattering, where two proportional constants,
for piezoelectric phonon scattering, where two proportional constants,
![]() and
and![]() , are used as the fitting parameters,
, are used as the fitting parameters, ![]() is the reciprocal of the Debye screening
is the reciprocal of the Debye screening
length, and ![]() and
and ![]() are the static dielectric constant and electron density, respectively.
are the static dielectric constant and electron density, respectively. ![]() (screening effect) decreases (increases) with increasing electron density.
(screening effect) decreases (increases) with increasing electron density.
The electron spin relaxation time in GaAs was calculated numerically for ![]() at the sub and edge (
at the sub and edge (![]() ) in the quantum limit. Figure 2 shows the electron density dependence of the electron spin relaxation times by piezoelectric acoustic and optical phonon scattering at
) in the quantum limit. Figure 2 shows the electron density dependence of the electron spin relaxation times by piezoelectric acoustic and optical phonon scattering at ![]() for
for![]() ,
, ![]() , and
, and![]() , where Matthiessen’s rule [19] was adopted to add the relaxation time by piezoelectric phonon scattering (
, where Matthiessen’s rule [19] was adopted to add the relaxation time by piezoelectric phonon scattering (![]() ) and that by optical phonon scattering (
) and that by optical phonon scattering (![]() ) to the total spin relaxation time (
) to the total spin relaxation time (![]() ) as
) as![]() . The spin relaxation time increases with increasing electron density because the spin relaxation time is proportional to the inverse of the relaxation rate, which decreases with increasing screening effect as the electron density is increased. The electron spins are relaxed mainly by optical phonon scattering at high electron densities and piezoelectric phonon scattering at relatively low electron densities.
. The spin relaxation time increases with increasing electron density because the spin relaxation time is proportional to the inverse of the relaxation rate, which decreases with increasing screening effect as the electron density is increased. The electron spins are relaxed mainly by optical phonon scattering at high electron densities and piezoelectric phonon scattering at relatively low electron densities.
![]()
Figure 1. Diagrammatic representation of the first and third terms in Equation (1). A photon with frequency ![]() is absorbed (emitted) during the forward (backward) process in a loop and a phonon with frequency
is absorbed (emitted) during the forward (backward) process in a loop and a phonon with frequency ![]() is absorbed (emitted) from (to) the spring during the lower (upper) half circle process. The red (left) and blue (right) processes correspond to the spin flipping and conserving processes, respectively.
is absorbed (emitted) from (to) the spring during the lower (upper) half circle process. The red (left) and blue (right) processes correspond to the spin flipping and conserving processes, respectively.
![]()
Figure 2. Electron density dependence of the electron spin relaxation time in GaAs at ![]() and
and![]() . The electron spins are relaxed mainly by the piezoelectric phonons at relatively low electron densities and the optical phonons at high electron densities. The black circles denote the results reported by Oertel et al. [9]
. The electron spins are relaxed mainly by the piezoelectric phonons at relatively low electron densities and the optical phonons at high electron densities. The black circles denote the results reported by Oertel et al. [9]
The energy of optical phonon is almost constant and that of piezoelectric phonon is dependent on the wave vector as ![]() where
where ![]() is the speed of sound. Therefore,
is the speed of sound. Therefore, ![]() for piezoelectric phonon scattering and
for piezoelectric phonon scattering and ![]() for optical phonon scattering. Figure 3 and Figure 4 show the q-dependence of
for optical phonon scattering. Figure 3 and Figure 4 show the q-dependence of ![]() for several electron densities. The spin relaxation times by piezoelectric phonon and optical phonon scattering increase because
for several electron densities. The spin relaxation times by piezoelectric phonon and optical phonon scattering increase because ![]() decreases with increasing electron density. The spin relaxation time increases with increasing number of phonons and the number of piezoelectric phonon decreases within creasing q, whereas the number of optical phonons is independent of q. Therefore, the spin relaxation time by piezoelectric phonon scattering increases more sharply than that by optical phonon scattering because the maximum points of
decreases with increasing electron density. The spin relaxation time increases with increasing number of phonons and the number of piezoelectric phonon decreases within creasing q, whereas the number of optical phonons is independent of q. Therefore, the spin relaxation time by piezoelectric phonon scattering increases more sharply than that by optical phonon scattering because the maximum points of ![]() are shifted to the right and the number of piezoelectric phonon contributing strongly to the spin relaxation decreases with increasing electron density.
are shifted to the right and the number of piezoelectric phonon contributing strongly to the spin relaxation decreases with increasing electron density.
The electron density dependence of the spin relaxation time at relatively low electron densities is similar to the experimental result reported by Oertel et al. [9] (the black circles in Figure 2). On the other hand, some experimental results [20] - [22] showed that the spin relaxation time increases with increasing carrier density and then decreases after reaching a maximum value at approximately![]() . Therefore, the discrepancy at relatively high electron densities (
. Therefore, the discrepancy at relatively high electron densities (![]() ) can be corrected if the electron-electron interaction is considered because the spin relaxation time (rate) by the electron-electron interaction decreases (increases) with increasing electron density. Figure 5 shows the temperature dependence of the relaxation relaxation times for different electron densities. The spin relaxation time decreases with increasing temperature because the number of phonons increases with increasing temperature. The spin relaxation time by piezoelectric phonon scattering decreases more sharply with increasing electron density than that by optical phonon scattering for the same reason shown in Figure 2.
) can be corrected if the electron-electron interaction is considered because the spin relaxation time (rate) by the electron-electron interaction decreases (increases) with increasing electron density. Figure 5 shows the temperature dependence of the relaxation relaxation times for different electron densities. The spin relaxation time decreases with increasing temperature because the number of phonons increases with increasing temperature. The spin relaxation time by piezoelectric phonon scattering decreases more sharply with increasing electron density than that by optical phonon scattering for the same reason shown in Figure 2.
4. Conclusions
This study calculated the electron spin relaxation time in a system of electrons interacting with piezoelectric acoustic and optical phonons through phonon-modulated spin-orbit coupling using the formula for the electron spin resonance obtained using the Kang-Choiprojection-Reduction (KCPR) method. The electron density dependence of the spin relaxation time was determined by ![]() and the distribution functions. The electron spin re-
and the distribution functions. The electron spin re-
laxation in GaAs was caused mainly by optical phonon scattering at high electron densities and piezoelectric phonon scattering at relatively low electron densities. The spin relaxation time decreased with increasing temperature and the electron density affected the electron spin relaxation differently according to temperature. The spin relaxation time increased with increasing electron density due to the screening effect. The meaning of two fit
![]()
Figure 5. Temperature dependence of the electron spin relaxation times in GaAs for several electron densities at![]() . The relaxation times decrease with different exponents for different electron densities as the temperature is increased.
. The relaxation times decrease with different exponents for different electron densities as the temperature is increased.
ting parameters, ![]() and
and![]() , was unclear at the present time. They affected the magnitude of the spin relaxation and it was inferred that they were related with the piezoelectric coupling constant (
, was unclear at the present time. They affected the magnitude of the spin relaxation and it was inferred that they were related with the piezoelectric coupling constant (![]() ) and Fröhlich coupling constant (
) and Fröhlich coupling constant (![]() ), respectively.
), respectively.
On the other hand, the spin relaxation time will decrease if the electron-electron interaction is considered at high electron densities. Therefore, it is expected that the electron spin relaxation time will increase with increasing electron density and then decrease after reaching a maximum value. Although it has been reported that the DP mechanism is important in a metallic regime [3] [23] for bulk III-Vn-type semiconductors, it is inferred that the DP mechanism can be quenched by an applied magnetic field or the (Dresselhaus) spin-orbit coupling term in conduction band can be suppressed at low electron densities. The formula used in this paper is applicable to the phonon-modulated spin-orbit interaction, which is dominant scattering mechanism at low electron density. Therefore, the formula is applied to GaAs at low electron density. By the Matthiessen’s rule, the total spin relaxation time (![]() ) is given by
) is given by![]() , where
, where ![]() is the spin relaxation time by the EY mechanism and
is the spin relaxation time by the EY mechanism and ![]() is the spin relaxation times by the other mechanisms including the “Dyakonov-Perel” (DY) mechanism. Therefore, small spin relaxation time corresponds to the dominant spin relaxation mechanism and the spin relaxation time by a single spin relaxation mechanism must exceed the experimental result. In conclusion, this paper shows that the dominant spin relaxation mechanism in bulk GaAs at low electron density is EY mechanism (Figure 1). The discrepancy between the present result and the experimental data [9] at high electron density may be corrected if other spin relaxation mechanisms such as electron-electron interaction and the DY mechanism or Marqulis and Marqulis (MM) mechanism [24] are considered. These will be examined using the present KCPR method in the future.
is the spin relaxation times by the other mechanisms including the “Dyakonov-Perel” (DY) mechanism. Therefore, small spin relaxation time corresponds to the dominant spin relaxation mechanism and the spin relaxation time by a single spin relaxation mechanism must exceed the experimental result. In conclusion, this paper shows that the dominant spin relaxation mechanism in bulk GaAs at low electron density is EY mechanism (Figure 1). The discrepancy between the present result and the experimental data [9] at high electron density may be corrected if other spin relaxation mechanisms such as electron-electron interaction and the DY mechanism or Marqulis and Marqulis (MM) mechanism [24] are considered. These will be examined using the present KCPR method in the future.