Transformation Formulas for the First Kind of Lauricella’s Function of Several Variables ()
Received 16 May 2016; accepted 24 June 2016; published 27 June 2016

1. Introduction
In 1994, Lavoie et al. [2] , obtained the following generalization of the classical Dixon’s theorem for the series :
:
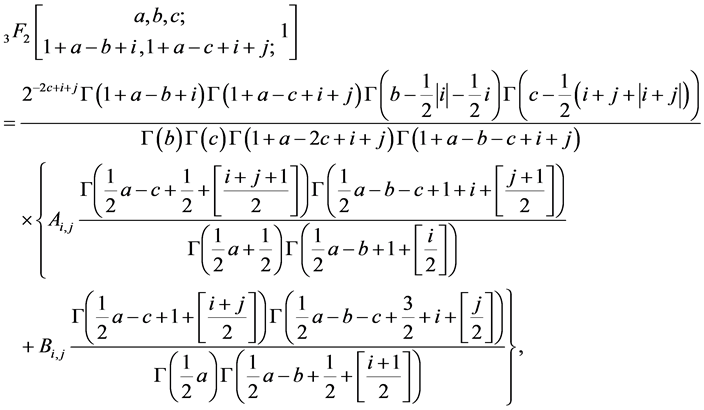 (1.1)
(1.1)
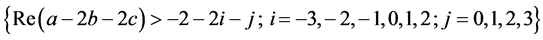 ,
,
where 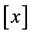 denotes the greatest integer less than or equal to x and
denotes the greatest integer less than or equal to x and 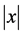 denotes the usual absolute value of x. The coefficients
denotes the usual absolute value of x. The coefficients 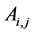 and
and 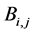 are given respectively in [2] . When
are given respectively in [2] . When , (1.1) reduces immediately to the classical Dixon’s theorem [3] , (see also [4] )
, (1.1) reduces immediately to the classical Dixon’s theorem [3] , (see also [4] )
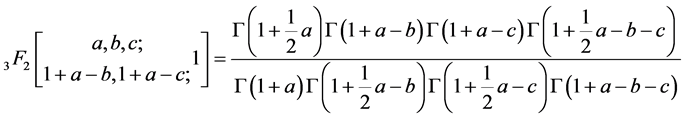 (1.2)
(1.2)
We recall that the first kind of the Lauricella hypergeometric function of ![]() -variables
-variables ![]() is defined as [5] :
is defined as [5] :
![]() (1.3)
(1.3)
![]() ,
,
where ![]() is the Pochhammer’s symbol defined by [5]
is the Pochhammer’s symbol defined by [5]
![]() (1.4)
(1.4)
When![]() , (1.3) reduces to the Lauricella function of 2r-variables
, (1.3) reduces to the Lauricella function of 2r-variables ![]()
![]() (1.5)
(1.5)
![]() .
.
Clearly, we have![]() , where F2 is Appell’s double hypergeometric function [5]
, where F2 is Appell’s double hypergeometric function [5]
![]() (1.6)
(1.6)
Next, we recall that the generalized Lauricella function of several variables is defined as [5] :
![]() (1.7)
(1.7)
where
![]() (1.8)
(1.8)
the coefficients![]() ,
, ![]() ,
,![]() ;
;![]() ,
,![]() ;
; ![]() for all
for all
![]() are real and positive;
are real and positive; ![]() abbreviates the array of A parameters;
abbreviates the array of A parameters; ![]() abbreviates
abbreviates
the array of ![]() parameters
parameters ![]() for all
for all ![]() with similar interpretations for
with similar interpretations for ![]()
and ![]()
![]() . Note that, when the coefficients in Equation (1.7) equal to 1, the genera-
. Note that, when the coefficients in Equation (1.7) equal to 1, the genera-
lized Lauricella function (1.7) reduces to the following multivariable extension of the Kampé de Fériet function [5] :
![]() (1.9)
(1.9)
where
![]() . (1.10)
. (1.10)
In our present investigation, we shall require the following results [5] :
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
2. Main Result
In this section, the following transformation formula will be established:
Theorem 2.1. For![]() , the following formula for Lauricella’s function
, the following formula for Lauricella’s function ![]() holds true:
holds true:
![]() (2.1)
(2.1)
where
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
The coefficients ![]() and
and ![]() can be obtained from the tables of Ai,j and Bi,j given in [2] by replacing a and c by
can be obtained from the tables of Ai,j and Bi,j given in [2] by replacing a and c by ![]() and
and![]() , also the coefficients
, also the coefficients ![]() and
and ![]() can be obtained from the same tables of Ai,j and Bi,j by replacing a and c by
can be obtained from the same tables of Ai,j and Bi,j by replacing a and c by ![]() and
and ![]() respectively.
respectively.
Proofs.
In order to prove the Theorem 2.1, let us first prove the following result:
![]() (2.5)
(2.5)
To prove (2.5), denoting the left hand side of (2.5) by I, expanding ![]() in a power series as in (1.6) and using the result [5] :
in a power series as in (1.6) and using the result [5] :
![]() ,
,
we have
![]() .
.
Now, using the elementary identities [5]
![]()
![]() ,
,
we have
![]() .
.
This completes the proof of (2.5).
Proof of Theorem 2.1. Denoting the left hand side of (2.1) by S, expanding ![]() in a power series as in (1.3), adjusting the parameters, using the results (1.11) and (2.5) and by repeating this procedure r-times, we have
in a power series as in (1.3), adjusting the parameters, using the results (1.11) and (2.5) and by repeating this procedure r-times, we have
![]()
where
![]()
Now, separating into even and odd powers of ![]() by using the elementary identity [5]
by using the elementary identity [5]
![]() ,
,
we have
![]()
Finally, if we use the result (1.1), then we obtain the right hand side of the Theorem 2.1. This completes the proof of the Theorem 2.1.
Remark. Taking x = 0 in (2.1), we deduce the following formulas:
Corollary 2.1. For![]() , the following formula for Lauricella’s function
, the following formula for Lauricella’s function ![]() holds true:
holds true:
![]() (2.6)
(2.6)
3. Applications
1) In (2.1) if we take r = 1, then we get a known extension formulas [6] for Lauricella’s function of three variables ![]() for
for ![]()
2) In (2.1), if we take![]() , we have
, we have
![]() (3.1)
(3.1)
Now, in (3.1) if we use the results (1.12)-(1.16) and simplify, we obtain the following transformation formula:
![]() (3.2)
(3.2)
which for![]() , reduces to
, reduces to
![]() (3.3)
(3.3)
3) Similarly, in (2.6), if we take![]() , we have
, we have
![]() (3.4)
(3.4)
which is a generalization of a known result of Bailey [7]
![]() . (3.5)
. (3.5)
Further, in (3.4) if we take![]() , then we get
, then we get
![]() (3.6)
(3.6)
4. Conclusion
We conclude our present investigation by remarking that the main results established in this paper can be applied to obtain a large number of transformation formulas for the first kind of Lauricella’s function of several variables![]() . Further, in the formulas (2.1) and (2.6), if we take
. Further, in the formulas (2.1) and (2.6), if we take![]() , then we can obtain two new families of transformation formulas for Lauricella’s functions of several variables
, then we can obtain two new families of transformation formulas for Lauricella’s functions of several variables
![]()
and
![]()
for![]() .
.