Received 24 May 2016; accepted 21 June 2016; published 24 June 2016

1. Introduction
The g-factor for an electron [1] is actually composed of two elements. The first element is the “bare” g-factor of exactly 2 and then the second element is a small correction to this, the anomalous magnetic moment. Total electron g-factor = 2 × (1.00116) = 2.00232. The anomalous magnetic moment correction of 1.00116 [2] is best explained by the virtual photons of QED theory [3] (see section 5 of the discussion section). In this paper, only the roots of the “bare” g-factor are investigated since the anomalous corrections due to QED’s virtual photons represent a different entity, the value of which varies from particle to particle. The reason that the electron has a bare g-factor of exactly 2 rather than 1 has been a source of mystery ever since spin was discovered. This paper should help solve this mystery.
What is the electron’s g-factor? The g-factor is a part of the calculation for the gyromagnetic ratio [4] , which is the ratio of the magnetic moment of a particle to the angular momentum of the same particle. G-factors are used for example in equations to calculate the various Larmor frequencies for MRI imaging purposes. Feynman shows, with a very simple equation, that if the mass and charge of an electron are distributed equally about a given radius, then the “classical” g-factor for the electron must be exactly “1” [5] , and in fact for calculations where the electron is orbiting a nucleus, the orbital g factor is indeed exactly one.
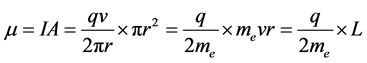 (Feynman) [5] (1)
(Feynman) [5] (1)
 = Magnetic moment (I = current, A = area enclosed by I, q = electron charge,
= Magnetic moment (I = current, A = area enclosed by I, q = electron charge,  = electron mass)
= electron mass)
L = angular momentum.
Therefore, 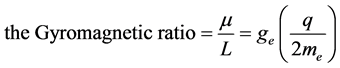 where the g-factor
where the g-factor 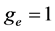 (2)
(2)
1.1. History of the g-Factor
A problem arose in the early days of trying to make quantum mechanical equations fit reality. It became apparent from experiments that the electron’s internal g-factor (as opposed to it’s orbital g-factor) needed to be 2 instead of 1.
i.e. the electron’s Gyromagnetic ratio =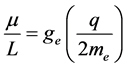 , Where
, Where 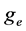 takes the value of 2 rather than 1.
takes the value of 2 rather than 1.
When Uhlenbeck and Goudsmit first discovered electron “spin”, they proposed that an electron has a magnetic moment due to a physically spinning sphere [6] but this led to two problems; First; a quick calculation based on the existing classical spherical model of the electron [7] showed that even if the charge were only on the surface of that sphere, it would need to exceed the speed of light in order to produce the correct magnetic moment [8] . The second problem was that the Fine-Structure and Zeeman spectral lines could not be accounted for correctly with a g-factor of one. i.e. only with a bare g-factor of “2”, (combined with a separate relativistic Thomas correction) could quantum mechanical equations reproduce the correct spectral lines [9] .
Note: See section 3 of the Discussions at end of paper for Dirac’s later insight into the mathematical necessity for the g-factor of 2 as well as the Thomas correction.
When Uhlenbeck and Goudsmit realized that the surface of their sphere would need to exceed the speed of light in order to produce the correct magnetic moment they had no explanation for how this could work, so they just submitted a note in their spin paper [6] explaining that there was a superluminal velocity issue. Note: The superluminal velocity problem goes away if one uses the Charged Electromagnetic Wave Loop (CEWL) model for the electron [10] , but first it is interesting to explore why Uhlenbeck and Goudsmit relied on a spherical model for the electron. They probably did so for the simple reason that a spherical model was already in use by other physicists, i.e. the classical radius model of 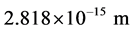 [7] that had been developed by Lorentz before spin was discovered. Another reason they used a spherical model was that they (incorrectly) thought that the necessary g-factor of 2 could be arrived at by using a surface charged spherical model. At the suggestion of their mentor Ehrenfest, they had used an existing g-factor calculation, previously done by another famous physicist [6] , which suggested that the necessary g factor of 2 could be accounted for by assuming that the charge of an electron resides only on the surface of a solid sphere. This previous calculation, which they included in their famous spin paper, produced the correct g-factor of two, which seemed to support the spherical model. However, a correct calculation, as shown below, will show that their spherical model would actually produce a g-factor of 5/3 (too small).
[7] that had been developed by Lorentz before spin was discovered. Another reason they used a spherical model was that they (incorrectly) thought that the necessary g-factor of 2 could be arrived at by using a surface charged spherical model. At the suggestion of their mentor Ehrenfest, they had used an existing g-factor calculation, previously done by another famous physicist [6] , which suggested that the necessary g factor of 2 could be accounted for by assuming that the charge of an electron resides only on the surface of a solid sphere. This previous calculation, which they included in their famous spin paper, produced the correct g-factor of two, which seemed to support the spherical model. However, a correct calculation, as shown below, will show that their spherical model would actually produce a g-factor of 5/3 (too small).
For a sphere of; M = mass, 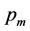 = density, w = angular frequency, the angular momentum “J” is:
= density, w = angular frequency, the angular momentum “J” is:
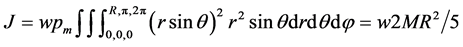 (3)
(3)
For the same sphere, if charge Q resides only on the surface, the magnetic moment “u” is:
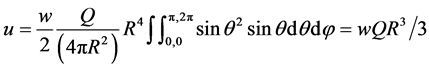 (4)
(4)
Therefore 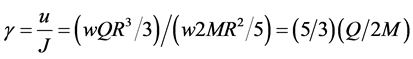 (5)
(5)
If the surface-charged-spherical model produces a g-factor of 5/3 instead of the necessary 2, then it can’t be correct. But in those early years of quantum mechanics this mistake was not known, and since it looked right, people moved on with the right answer of 2 for the wrong reason. The superluminal conflict was dismissed at the time by just saying the electron has an “intrinsic” spin that can’t be understood classically.
Both the erroneous g-factor explanation and the superluminal velocity issues go away if the Charged-Elec- tromagnetic-Wave-Loop (CEWL) Model is used, i.e. the charge can now rotate within Einstein’s laws of relativity, and the g-factor of 2 can easily be derived from the model. It can also be demonstrated that no other shape or diameter besides the CEWL model can get rid of the superluminal violations of relativity. The CEWL model, as described in the paper “An Electron Model Consistent with Electron-Positron Pair Production from High Energy Photons” [10] will also exactly generate the correct de Broglie matter-wave base frequency to over 6 decimal places while matching the known magnetic moment of the electron to over 6 decimal places simultaneously (Getting the de Broglie frequency to match was another problem with the original spherical superluminal model). Below is a quick summary of the CEWL model followed by some diagrams to help explain how it generates the correct g-factor of 2.
1.2. The CEWL Model
The CEWL model starts with the premise that since electron-positron pairs form from purely electromagnetic photons (of energy > 1.022 Mev [11] ), and since the resulting pairs of electrons and positrons (of energy 0.511 Mev each) have the same electromagnetic nature (as witnessed by their de Broglie wavelengths), then they must have the same electromagnetic wave nature as the photons from which they originated, except for one detail; The magnetic field lines of electrons and positrons can close back on themselves allowing matter to exist at rest, whereas the magnetic field lines of photons do not (and hence the magnetic and electric fields of photons chase each other forward at the speed of light).
Note: Maxwell was the first to be able to calculate the speed of light “c” with his equation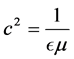 , where
, where 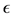
and 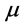 are the electric and magnetic permittivity constants of free space. Where does the mass come from? One can combine Maxwell’s equation above with Einstein’s
are the electric and magnetic permittivity constants of free space. Where does the mass come from? One can combine Maxwell’s equation above with Einstein’s ![]() to get
to get ![]() where mass can be equated to the purely electromagnetic terms on the right. The electromagnetic energy tensor equations of general relativity theory are also shown to contribute to space time distortion exactly the same as mass does (see below).
where mass can be equated to the purely electromagnetic terms on the right. The electromagnetic energy tensor equations of general relativity theory are also shown to contribute to space time distortion exactly the same as mass does (see below).
2. From Photon to Fermion
2.1. From Photon
Modern modelling of photons generally focuses on the “potential” E and B fields (Electric and Magnetic fields), but as Maxwell first envisioned a photon, it is actually composed of a charge separation spiralling through space at the speed of light [12] (the electric permittivity constant of free space Î describes the capacitance like ability to induce a charge separation in free space). Figure 2 “before” shows how Maxwell envisioned the charge separations of a photon (the spiral can be either right hand or left polarity). Note: The cross section perpendicular to the direction of travel is of the general form of an ellipse [13] , with “circularly” polarized light having a circular elliptical cross section, and regular “polarized” photons having a more elongated elliptical cross section (circularly polarized photons can be changed into “regular” elliptically polarized photons and “regular” photons can be changed to circularly polarized by sending the photon through non-linear optics such as “quarter wave plates” [14] ) The right hand or left hand spiral “spin” rotation direction however stays constant unless the photon is reflected by a mirror etc.)
2.2. To Fermion
When high energy gamma ray photons (of at least 1.011 Mev energy) collide with matter, they produce elec-
tron-positron pairs [11] (see Figure 1).
The CEWL model for electron positron pair production is shown below by the transition from a high energy photon in Figure 2 “before” to two charged loops in Figure 2 “after”. The positively charged loop is a Positron and the negatively charged loop is an Electron. Due to the original spin rotation of each at formation, the magnetic fields are opposed at the moment of formation, allowing the electron and positron to separate despite their enormous electrostatic attraction at that scale. The original paper [10] contains the math to show that the opposing magnetic field at initial formation of an electron-positron pair would exceed the electrostatic attraction between them.
The simplest definition of the g-factor of an electron is that it represents the ratio between the radius of the rotating charge, and the radius of the rotating mass. For example if we look at an electron orbiting in a circle, we know that it will generate a bare g-factor of one because the mass and the charge are both orbiting at the same radius around the atom. The CEWL electron model may look similar, with a rotating charged component, but unlike the case where an electron orbits a nuclei (where all the mass of the electron contributes to rotational mass), in the CEWL model only half the electron’s mass contributes to rotational mass. The electric energy, i.e. the rotating charge component, contributes to the rotational mass, but the magnetic energy, because the direction of its components only act in a plane perpendicular to the direction of the charge, as shown in Figure 3, the magnetic energy will not add “rotational” mass. (See the difference between electric energy mass and magnetic energy mass below).
2.3. Electromagnetic Energy and Mass
MIT Physics professors’ emeriti Slater & Frank have solved Maxwell’s Electromagnetic equations for the general case of plane wave propagation of photons to show that the total Electro-Magnetic Energy Density in free space, i.e. with no resistive component is:
![]() [16] (6)
[16] (6)
As further explained by Slater & Frank, the average magnetic component (the B half of this equation) is only greater than the average Electric component when a resistive component is present [16] . In any given rest frame, photons and electrons do not lose energy, i.e. internally they have no resistive component, so therefore if the electrons and positrons maintain the same electromagnetic wave nature as the photon from which they originated, then the average electric energy must exactly equal the average magnetic energy in both cases.
Using![]() , one can divide the above Energy density Equation (6) by
, one can divide the above Energy density Equation (6) by ![]() to get Mass density:
to get Mass density:
![]()
Figure 1. Electron-positron pair production in aluminum [15] .
![]() Figure 2 “Before” and Figure 2 “After” show the transition from a 1.022 Mev photon to positive and negative loops that are closed and repelling away from each other magnetically. The positive loop is a positron and the negative loop is an electron. Note: The wavelength in Figure 2.“Before” and the loop diameters in Figure 2. “After” are roughly in scale relative to each other, but the other dimensions such as the size, shape and distribution of the charged regions would differ from what is shown. Due to the compressive forces of the magnetic field lines inside and outside the loop, the thickness of this charged layer would most likely be a very thin in the same way that a barrel hoop is, with the charge most likely sinusoidally distributed as it rotates around the loop.
Figure 2 “Before” and Figure 2 “After” show the transition from a 1.022 Mev photon to positive and negative loops that are closed and repelling away from each other magnetically. The positive loop is a positron and the negative loop is an electron. Note: The wavelength in Figure 2.“Before” and the loop diameters in Figure 2. “After” are roughly in scale relative to each other, but the other dimensions such as the size, shape and distribution of the charged regions would differ from what is shown. Due to the compressive forces of the magnetic field lines inside and outside the loop, the thickness of this charged layer would most likely be a very thin in the same way that a barrel hoop is, with the charge most likely sinusoidally distributed as it rotates around the loop.
Figure 2.“Before” Photon λ = 12.13 × 10−13 m. “After” Loop Diam = 7.723 × 10−13 m .
![]()
Figure 3. The Magnetic “B” field lines which are due to the rotation of the charge inside an electron/positron have no component in the direction of the “I” current/charge rotation and hence can add no rotational energy/mass. Note: the positive charge in a positron would rotate as shown, but the negative charge of an electron would rotate in a direction opposite to that of the “I” arrow in order to conform to the North and South polarity shown. Due to its electromagnetic wave nature, the charge amount would most likely vary sinusoidally as it progresses around the loop at the speed of light (inside a loop of much smaller volume relative to radius than shown in this figure).
![]() (7)
(7)
Note: Using Maxwell’s ![]() to get rid of
to get rid of![]() , it is easy to show that this is exactly the same equation as the
, it is easy to show that this is exactly the same equation as the
Electromagnetic Stress-Energy tensor form for mass used in Einstein’s General Relativity [17]
Electromagnetic Tensor equation for Mass: ![]() [17] (8)
[17] (8)
Since only half the electromagnetic mass contributes to angular momentum, then we can simply substitute L/2 for L into Feynman’s electron gyromagnetic equation, Equation (2) above, and we get:
![]() (9)
(9)
The electron g-factor ![]() is now twice classical, i.e.
is now twice classical, i.e. ![]() instead of 1.
instead of 1.
Note: See the Conclusions section for a more detailed explanation.
This is similar to the Faraday Paradox in which a magnet rotating inside a conductive loop can impart no rotational energy out to the loop. [18] .
3. No Other Model Can Match Reality without Violating either Einstein’s
General Relativity or Maxwell’s Equations
The fact that the Tensor equations of general relativity show that the space time distortions due to electromagnetic energy density are no different from the space time distortions of “mass” suggests that they are one and the same. Furthermore, if we invoke some mystical “other” form of mass such as a sphere or disk on which the charge rotates, we run into a problem; If there is another form of “mass” (besides the electromagnetic energy components), then by Einstein’s![]() , that mass would come at the expense of the electromagnetic energy. We know that the base de Broglie frequency of an electron is exactly the same as the frequency of a purely electromagnetic photon of equal energy [10] , so this by itself should rule out any subtraction from the original electromagnetic energy (with which to make this different form of matter). Additionally, the charge cannot rotate at any diameter except the CEWL diameter (see below), and since the magnetic energy of any loop of moving charge would, of necessity, be both inside and outside the loop (see Figure 3), then the total mass cannot be completely inside the loop diameter. This rules out a charge on the edge of a disk of some hypothetical different form of mass for example. This also rules out any other exotic shape where all the mass is completely inside the CEWL diameter.
, that mass would come at the expense of the electromagnetic energy. We know that the base de Broglie frequency of an electron is exactly the same as the frequency of a purely electromagnetic photon of equal energy [10] , so this by itself should rule out any subtraction from the original electromagnetic energy (with which to make this different form of matter). Additionally, the charge cannot rotate at any diameter except the CEWL diameter (see below), and since the magnetic energy of any loop of moving charge would, of necessity, be both inside and outside the loop (see Figure 3), then the total mass cannot be completely inside the loop diameter. This rules out a charge on the edge of a disk of some hypothetical different form of mass for example. This also rules out any other exotic shape where all the mass is completely inside the CEWL diameter.
No other diameter except a circular loop of exactly the CEWL diameter can fit reality. This is because unless the charge is rotating in a circular loop of diameter ![]() Meter, at the speed of light, the correct magnetic moment and the correct de Broglie frequency will not be generated simultaneously. Only at precisely the correct CEWL diameter, will both match reality to over 6 decimal places [10] . Any smaller diameter requires superluminal velocities to generate the correct magnetic moment, and any larger diameter requires superluminal velocities to generate the correct de Broglie frequency. For the same reason, any loop besides a circle doesn’t work either; If for example we investigate an oval loop (instead of a circular loop), who’s transit frequency at the speed of light matches the de Broglie frequency, then the magnetic moment will be too small due to the fact that the magnetic moment depends on multiplying the amperage times the area enclosed inside the loop. It is only at precisely the CEWL diameter that all elements of reality can be met exactly and simultaneously [10] .
Meter, at the speed of light, the correct magnetic moment and the correct de Broglie frequency will not be generated simultaneously. Only at precisely the correct CEWL diameter, will both match reality to over 6 decimal places [10] . Any smaller diameter requires superluminal velocities to generate the correct magnetic moment, and any larger diameter requires superluminal velocities to generate the correct de Broglie frequency. For the same reason, any loop besides a circle doesn’t work either; If for example we investigate an oval loop (instead of a circular loop), who’s transit frequency at the speed of light matches the de Broglie frequency, then the magnetic moment will be too small due to the fact that the magnetic moment depends on multiplying the amperage times the area enclosed inside the loop. It is only at precisely the CEWL diameter that all elements of reality can be met exactly and simultaneously [10] .
4. Discussions
1) When the Grand Master of Physics Lorentz first heard of Uhlenbeck’s and Goudsmit’s ground-breaking spin paper, he pointed out a possible problem; i.e. since the magnetic energy is roughly the magnetic moment squared
divided by the radius cubed, i.e. ![]() [6] , then the radius would have to be roughly
[6] , then the radius would have to be roughly ![]() meter i.e. too big. This
meter i.e. too big. This
had also reinforced the concept that the spin must be “intrinsic” and physics moved on. But apparently Lorentz’s only objection to that size was that it conflicted with the then current estimates of atomic nuclei cross sections, and since he was aware that electron’s can be emitted from nuclei (beta decay), hence the size didn’t make sense to him. But the original CEWL model paper shows that the Muon and Tau higher energy states of the electron have a much smaller size [10] , and since the electron would most likely be in the form of a Muon while it still resides inside a neutron, Lorentz’s size estimate would not actually be the conflict he thought it to be. Lorentz’s rough estimate of size was not far from the Electron’s CEWL loop radius of ![]() Meter. The CEWL model predicts that the Muon form of the electron would be about 207 times smaller than the electron [10] , i.e. roughly
Meter. The CEWL model predicts that the Muon form of the electron would be about 207 times smaller than the electron [10] , i.e. roughly ![]() Meter (much closer to what Lorentz was expecting).
Meter (much closer to what Lorentz was expecting).
2) Two other distinguished physicists have suggested the same diameter as that of the CEWL model: Just before publishing the original paper, a book by Mac Gregor [19] was discovered, in which he had proposed a spherical model of exactly the same diameter as the CEWL model. Mac Gregor, (who studied under Uhlenbeck), suggests that a charge spins around the equator of this spherical model in order to produce the correct magnetic moment for an electron. The CEWL model differs in that it doesn’t use a spherical “scaffolding” to support the charge as it rotates since it has not been demonstrated what the spherical scaffolding would be made of or how it would form.
Another paper [20] , written in 1952 by the distinguished MIT professor emeritus Kerson Huang, has just come to light as well. In his 1952 paper Professor Huang explores the same diameter within the context of quantum mechanical equations. Professor Huang uses the same diameter for the same reason, i.e. because it generates the correct magnetic moment for the electron, but his interpretation of the electron is different from the CEWL model in that by using the quantum mechanical approach, he does not address the internal structure of the electron itself, or what it might be made of, and suggests that the mysterious matter of the electron can be either physically localized or physically spread out over large regions of space depending on the measurement. The CEWL model by contrast addresses the internal structure of the electron itself and says that it is a charged electromagnetic wave internally. (See next section for a comparison to the quantum mechanical approach).
3) A few years after Uhlenbeck’s and Goudsmit’s ground breaking spin paper, the famous physicist Dirac was able to derive an amazing 4 × 4 matrix version of quantum mechanics which included relativity corrections, and was able to show that both the g-factor of 2 as well as the Thomas correction of 2 could both be inferred as necessary from his more advanced mathematical descriptions of the electron [21] . This is similar to the way that the speed of light “c” can be inferred from either Maxwell’s equations or Einstein’s ![]() equation). Dirac however was working from a quantum-mechanical approach, which did not require presenting a physical model for the electron in the same way that Maxwell had put forth a rotating charge model of the photon in order to explain how Maxwell’s equations would generate the speed of light for a photon. The end result was that even decades after Uhlenbeck’s and Guoudsmit’s discovery of spin, the g-factor of 2 was still viewed as a mysterious mathematical necessity. As Einstein famously said towards the end of his life, “You know, it would be sufficient to really understand the electron.” [19] .
equation). Dirac however was working from a quantum-mechanical approach, which did not require presenting a physical model for the electron in the same way that Maxwell had put forth a rotating charge model of the photon in order to explain how Maxwell’s equations would generate the speed of light for a photon. The end result was that even decades after Uhlenbeck’s and Guoudsmit’s discovery of spin, the g-factor of 2 was still viewed as a mysterious mathematical necessity. As Einstein famously said towards the end of his life, “You know, it would be sufficient to really understand the electron.” [19] .
The CEWL model matches all known values for the electron, so it is compatible with the amazing equations of quantum mechanics, but it goes a step further by proposing an internal structure for the electron itself. Quantum mechanical equations were developed to fit the known spectral line data generated by quantum energy jumps of electrons as they transition between orbital levels within the ecosystems of atoms (electrons have characteristic wavelengths as they move through space, and because of this, only atomic orbits whose circumferences are integer values of these wavelengths are stable). The quantum energy jump equations address the energy level jumps within the ecosystem of an atom, but do not address the internal structure of the electron itself. Richard Feynman, one of the founders of QED theory, (one of the most advanced forms of quantum mechanics), lamented at the end of his 1985 book on QED that there is no theory that explains the masses of particles [3] . Other versions of quantum mechanics are also silent on what the internal structure of the electron might be. The CEWL model by contrast addresses the internal structure of the electron itself, showing it to be an electromagnetic wave internally, just like the photon from which it originated (with the only difference between a fermion and a photon being that the magnetic field lines of a fermion can close back on themselves allowing a fermion to exist a rest). The electromagnetic wave nature of the CEWL model, in addition to showing why the g-factor must be 2, also shows how the rotating charge would add both a positive and negative speed of light component to the average velocity of a moving electron as predicted by Dirac [21] , and also explains how the de Broglie wave nature of the electron can arise from the model [10] . (The de Broglie wave nature of the electron explains why quantum energy jumps are required within the ecosystem of atoms).
4) The CEWL model addresses the previously mysterious g-factor of 2 needed to make quantum mechanical equations fit reality, but how does this fit with the mysterious Pauli’s exclusion principle of quantum mechanics? And is it compatible with the mysterious “superposition of spin” demonstrated by the Stern Gerlach experiment [22] ? Here’s a quick and easy trick to show how everything fits together: Take two magnetic compasses as shown in Figure 4 “before” and then put one on top of the other as shown in Figure 4 “after”. Voila! One has spin up and the other has spin down! This is the nature of Pauli’s exclusion principle. Within the “ecosystem” of an atom, pairs of electrons within the same orbit interact with each other such that their magnetic field lines are minimized in the same way that the two compasses have done. This is a lower energy state than having both electrons “spin” in the same direction.
The heavier neutrons and protons of the nuclei have magnetic moments too, they are just much heavier than an electron. Imagine strapping a pound of lead to the needle of one of the compasses (assuming the heavy compass could still rotate freely); the two compasses would still align themselves as before, except that the lighter “electron” would respond to a magnetic field quicker than the heavy “nuclei”. In any atom, the first electron in any orbital pair would align itself with the nuclei, and the second would align itself with the first, and each successive electron pair in an atomic “ecosystem” would do likewise. The Stern-Gerlach experiment consisted of shooting randomly oriented silver atoms (which have one unpaired electron in the outer shell) through a strong magnet [22] . The
![]()
![]()
![]()
Figure 4. “Before” two isolated electrons. “After” electrons form pairs of one “Up” and one “Down”.
result was that the stream of silver atoms split into two streams and this result was used to demonstrate that electrons exist in a “superposition”. “Superposition” implies something mystical about an electron, but it’s not really that mysterious; what was really happening was that the heavy nuclei didn’t have time to react while going through the magnet, but the unpaired electron did. If the heavier nuclei were already somewhat aligned with the magnet, the electron flipped out of its normal state opposing the nuclei spin, and into a spin state closer to that of the nuclei (adding to the total magnetic moment). If on the other hand the nuclei happened to already be aligned somewhat opposite to the magnet, then the final orientation of the electron subtracted from the nuclei magnetic moment. The net effect is two magnetic states (of the atomic ecosystem) depending on whether the electron now adds to, or subtracts from, the original nuclei magnetic moment after going through the magnet (an electron by itself would not show a two state “superposition” since it would simply rotate into full alignment with the magnet).
5) The circular loop of the CEWL electron model is similar to the nature of an inductive loop antenna [23] in that the circumference around a loop antenna must match the wavelength of the received/transmitted electromagnetic radio wave photons. Likewise, the circumference of the CEWL model exactly matches the Compton wavelength of a photon of energy equal to that of an electron. (in the CEWL model, the electron has exactly the same nature as the electromagnetic photon that generated it, with the only difference being that the magnetic field lines have closed back on themselves allowing it to exist “at rest” rather than travel at the speed of light). Antenna theory subdivides electromagnetic interactions into 3 regions [24] ; 1) The “Near Field” where electromagnetic oscillations are induced near the antenna, but leads to no net loss of energy from the antenna (all “virtual photon” energy is reabsorbed by the antenna), 2) The “Fresnel” intermediate region, and 3) The “Far Field” where photons fully form and can propagate away (leading to net energy loss from the antenna). The “virtual photons” (and virtual particles) that start to form near the electron but then get immediately reabsorbed is the basis for how Feynman and Shwinger calculated the anomalous magnetic moment correction of 1.00116 for the electron’s g-factor [3] . The ability of electrons, positrons and other forms of matter to induce oscillations in the vacuum of free space is what distinguishes modern quantum type physics from the previous more “classical” interpretations of physics, i.e. interactions of particles with a pure vacuum cannot be calculated as simply “one-way” interactions, but rather the energy fluctuations of all the virtual photons (and virtual particles) induced near matter must also be calculated, both for their effect back on the original particle as well as for their effect on nearby photons and matter [3] .
By investigating the antenna nature of the CEWL model it may be possible to investigate, among other things, the directionality and polarity of the “virtual” photons of QED theory that are emitted (and immediately reabsorbed) in the vicinity of electrons. As semiconductors shrink down to sizes where ever smaller numbers of electrons are channelled through ever smaller channels, CEWL modelling of the antenna and spin characteristics at scales close to the CEWL size of the electron may provide insight into how to further reduce resistance losses in semiconductors.
6) The electron’s g-factor of 2 represents the highest gyromagnetic moment of any form of matter and this is most likely connected to the fact that the electron is an indivisible unit of matter and a building block for other forms of matter [10] . When for example the neutron’s g-factor is represented as −3.826, this does not mean that the gyromagnetic moment of a neutron is 3.826 times higher than an electron, i.e. it just represents an offset to an arbitrary gyromagnetic ratio equation. The g-factor equation for the heavier neutron looks similar to the electron’s equation, except that instead of using the charge and mass of the electron (which would require a g-factor correction 3 orders of magnitude smaller than the electrons g-factor), it instead arbitrarily uses the mass of one proton, ![]() (while still using the charge of one electron).
(while still using the charge of one electron).
This same arbitrary equation: ![]() [4] (10)
[4] (10)
Is used for neutrons and protons and all nuclei “For simplicity and consistency” [4] . In the same way that the electron’s g-factor gives a clue to its internal structure, the various g-factors of other nuclear components can most likely be investigated for information on how their internal building blocks are arranged.
5. Conclusions
By looking at how Feynman derived the electron’s gyromagnetic ratio in equation #2 from his equation #1, it is easy to see that when investigating an electron’s orbit around an atom, where both all the mass and all the charge of the electron orbit at the same radius around the atom, the bare g-factor must be exactly 1, so it has been a mystery why a bare g-factor of 2 is needed to make quantum mechanical equations fit reality. This paper shows that if a simple Charged-Electromagnetic-Wave-Loop (CEWL) model is used for the electron itself, whereby the electron maintains the same electromagnetic characteristics as the photon from which it originated, then it follows that only half of the electron’s mass contributes to the angular momentum inside the electron. This is due to the fact that the magnetic field lines inside the electron are perpendicular to the direction of the charge rotation internally (see Figure 3), and hence the magnetic energy half of the mass cannot add to the angular momentum inside the electron, which leads to the conclusion that the angular momentum inside the electron is exactly half of what it would be if the entire electromagnetic energy contributed to angular momentum (see Equations (6)-(8) and reference [16] ). This shows that inside the electron itself, the angular momentum as used by Feynman in Equation (2) would now need to take the value of L/2 instead of L, leading to a necessary correction to the other side of Feynman’s equation by increasing the g-factor to ![]() instead of 1 in order to keep the two halves of the equation equal. This explains the mystery of why quantum mechanical equations require an electron to have a bare g-factor of 2 rather than 1 in order to fit reality.
instead of 1 in order to keep the two halves of the equation equal. This explains the mystery of why quantum mechanical equations require an electron to have a bare g-factor of 2 rather than 1 in order to fit reality.
The CEWL model, in addition to explaining why a bare g-factor of 2 is needed for calculations involving the electron’s internal spin, also explains all other known values for the electron as well as showing how electron- positron pairs can form from high energy photons.
Acknowledgements
Many thanks to Robert V. Mulkern PhD for reviewing this paper as well as for the calculations to demonstrate that a surface charged spherical model can’t work, and for helpful discussions.