Aerodynamic Sound Radiated from Longitudinal and Transverse Vortex Systems Generated around the Leading Edge of Delta Wings ()
Received 14 May 2016; accepted 18 June 2016; published 21 June 2016
1. Introduction
The sound induced by turbulence in an unbounded fluid is generally called aerodynamic sound. With respect to aerodynamic sound, Lighthill [1] , Curle [2] and Howe [3] [4] have made their theoretical contributions to clarifying the relationship between turbulent flow and sound. Lighthill [1] transformed the Navier-Stokes and continuity equations to form an exact, inhomogeneous wave equation whose source terms are important only within the turbulent region. This equation is called Lighthill’s equation. In most applications of Lighthill’s theory it is necessary to generalize the solution to account for the presence of solid bodies in the flow. Curle [2] has made an extension to Lighthill’s general theory of aerodynamic sound so as to incorporate the influence of solid boundaries upon the sound field. Howe [3] [4] recast Lighthill’s equation in a form that emphasizes the prominent role of vorticity in the production of sound by taking the total enthalpy as the independent acoustic variable, which leads to the vortex sound equation. These theories have emphasized that unsteady motions of the vortex play a crucial role in the generation of aerodynamic sound.
Regarding the vortex, emphasis has been placed especially on longitudinal vortex which rotates about the axis whose direction coincides with the flow direction. In the automobile industry the reduction of aerodynamic noise becomes more and more important for the comfortable vehicle since noises caused by engine, power train, tires, and other noise sources have been steadily reduced in recent years. It is well known that the front pillar of an automobile is regarded as one of the most dominant area in generating aerodynamic noise due to strong longitudinal vortices. Separated flows behind the front pillar generate the longitudinal vortices. Based on the theories as mentioned above, many researchers have so far tried to reveal the generation mechanism of aerodynamic sound. Haruna, Nouzawa, Kamimoto and Sato [5] applied the Lighthill-Curle’s theory of aerodynamic sound to automobiles and experimentally estimated dipole noise emitted from the pressure fluctuations on the body surface. Recently Nouzawa, Li and Nakamura [6] have studied the mechanism of aerodynamic noise generated from front pillar and door mirror. Hamamoto, Okutsu and Yanagimoto [7] have investigated the effect of the external aerodynamic noise sources onto the interior noise around the front pillar where longitudinal vortices exist. Numerical approaches have also been conducted with delta wings and actual vehicles (Haruna, Hashiguchi, Kamimoto and Kuwahara [8] , Takeda and Ogawa [9] , Ogawa and Li [10] ). In addition to the aerodynamic engineering field, longitudinal vortex also has been focused in the heat transfer engineering field. Jacobi and Shah [11] reviewed enhancement of heat transfer through the use of longitudinal vortices. Recently Iwasaki, Hara and Honda [12] used longitudinal vortices for EGR (exhaust gas recirculation) system to cool down the temperature of exhaust gas from the engine.
There have been so many studies to reveal the generation mechanism of aerodynamic noise produced by longitudinal vortex. However, it has not yet been clarified that how the longitudinal vortex system has been generated and how this system produces the aerodynamic noise. The final objective of our study, therefore, is to simplify this specific aerodynamic noise problem to obtain a thorough understanding of how the longitudinal vortex is produced, and how the noise can be estimated quantitatively.
Ogawa and Takeda [15] have so far been investigating mechanism of generation and collapse of a longitudinal vortex system induced around the leading edge of a delta wing. As a second step, the present paper aims to clarify the difference between the longitudinal vortex system and the transverse vortex system in terms of their configurations, the distribution of pressure coefficients on the surface of the delta wings, the magnitude and the components of vorticity, and the characteristics of aerodynamic sound radiated from the longitudinal and the transverse vortex system. Theoretical discussion will be developed to reveal the source of aerodynamic sound from the perspective of Lighthill tensor, Reynolds stress, vortex sound, and Green’s function.
2. Visualization of the Vortex Systems by Running Water Channel
Figure 1 shows one of the delta wings employed for reproduction of the longitudinal and the transverse vortex system. The wing model has three dimensions with 260 mm long, 160 mm wide and 3 mm thick. The models have 6 tip angles of 40, 90, 110, 120, 130, and 140 degrees as shown in Figure 2. The models with 15 degrees as attack of angles were immersed in the running water channel shown in Figure 3. The uniform velocity of water flow is 0.2 m/s. The test section is 1500 mm wide × 800 mm high × 4000 mm long, which is large enough to visualize the flow around the delta wings.
Figure 4 depicts the longitudinal vortices and transverse vortices visualized by the hydrogen bubble method in the running water channel. The separated flows around the leading edge were rotating. Red lines indicate
![]()
Figure 1. Three dimensional delta wing used.
![]()
Figure 2. Six delta wings employed for flow visualization and their characteristic sizes are almost the same as that shown in Figure 1.
![]()
Figure 3. Running water channel (unit: mm).
![]()
Figure 4. The longitudinal vortex system and the transverse system visualized by the hydrogen bubble method.
rotating image of configuration of the vortex system. Chain line schematically shows rotating axes of the each vortex system. Two wings with the tip angles of 40 and 90 degrees show the longitudinal vortex system whose rotating axis is located in the flow direction has cone-shaped configurations. However, with the increase of tip angles, the cone-shaped configurations began to collapse around 110 degrees and over 120 degrees the vortex system shifted to the transverse vortex system whose shapes are no longer cone-shaped but elliptic with rotating axes vertical to the mean flow direction. This visualization method was able to clearly capture the change of vortex system from the longitudinal to the transverse vortex system. Although the spatial scale of the longitudinal vortex system is smaller than the transverse one, the rotating speeds of hydrogen bubbles in the longitudinal qualitatively seems to be faster than those in the transverse.
3. The Method of Numerical Simulation
As a next step, CFD will be employed to analytically investigate the structure of the longitudinal vortex. The study uses the software STAR-CCM+ with software V10.04.009. In the simulation, numerical delta wing model has six tip angles of 40, 90, 110, 120, 130, and 140 degrees just as in flow visualization experiment.
3.1. Numerical Method
This study employed RANS (Reynolds Averaged Navier-Stokes Simulation). This approach is valid when the maximum Mach number in the domain is less than 0.2 - 0.3. Eddy viscosity models use the concept of a turbulent viscosity to model the Reynolds stress tensor as a function of mean flow quantities. For the accurate simulation, Menter SST k-ω model was used as the hybrid models in the form that k-ω model was used close to the wall whereas the standard k-ε in the completely turbulent region was employed. The SST k-ω turbulence model is a two-equation eddy-viscosity model which has become very popular. The shear stress transport (SST) formulation combines the best of two worlds. The use of a k-ω formulation in the inner parts of the boundary layer makes the model directly usable all the way down to the wall through the viscous sub-layer, hence the SST k-ω model can be used as a Low-Re turbulence model without any extra damping functions. The SST formulation also switches to a k-ε behavior in the free-stream and thereby avoids the common k-ω problem that the model is too sensitive to the inlet free-stream turbulence properties. It therefore follows that SST k-ω model often merit it for its good behavior in adverse pressure gradients and separating flow. In the steady state analysis, the maximum step number is 3500. Reynolds number is defined in Equation (1), where mean air flow velocity U = 10 m/s, representative length L = 0.26 m, and kinematic viscosity ν = 1.43 × 10−5 m2/s and results in Re = 1.7 × 105. This implies that the flow is turbulent and Mach number is 0.029.
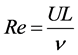(1)
3.2. Mesh Generation Method
Figure 5 shows the wing model in numerical wind tunnel. The models employed in the simulation have the tip angles of 40, 90, 110, 120, 130, and 140 degrees with three dimensions as shown in Figure 1. The characteristics of the vorticity in the two vortex systems were investigated at three sections, A, B, and C. The scale of the numerical wind tunnel is 600 mm × 600 mm × 1260 mm. The wind scale was determined so that the uniform
![]()
(a)![]()
(b)
Figure 5. The delta wing model in the numerical wind tunnel. (a) Side view; (b) Top view.
flows can be maintained around the delta wing model. The attack of angles for all the models are 15 degrees the same as that used in the running water channel. Total number of mesh ranges from 7.48 million to 8.11 million, depending on the tip angles of the model. Minimum mesh size is 0.25 mm in closest vicinity to the leading edge of the model. In generating mesh, the prism layer meshing method was adopted. This meshing method was used to optimize the mesh size in the boundary layer as shown in Figure 6. The prism layer mesh model is used with a core volume mesh to generate orthogonal prismatic cells next to the surface of the delta wing. This layer of cells is necessary to improve the accuracy of the flow solution. The prism layer mesh is defined in terms of its thickness, the number of cell layers, and the size distribution of the layers. In this study the total thickness of prism layer is 3 mm with five cell layers and prism layer closest to the model surface is 0.5 mm. To conduct the
![]()
(a)![]()
(b)
Figure 6. Mesh condition around the delta wing surface. (a) Prism layer close to the surface of the wing; (b) Distribution of wall Y+ on the wing surface.
simulation with higher accuracy, the thickness of prism layer was decided so that wall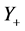 
can be less than 25 across the wing surface as shown in Figure 6. Wall 
indicates the dimensionless distance from the wall surface of the wing as defined in Equation (2), where 
is frictional velocity, y distance from the surface, and ν kinematic viscosity.
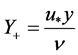(2)
4. Numerical Results and Discussion
4.1. Quantitative Characteristics of the Longitudinal and the Transverse Vortex System
Figure 7(a) shows the streamlines of the longitudinal vortex system and the transverse one generated behind the leading edge of the each delta wing with the tip angles of 40, 90, 110, 120, 130, and 140 degrees. In order to exactly grasp the streamlines which go through the region of the vortex systems, the streamlines was extracted so that total pressure coefficients Cpt could be less than 1.0 in the section C. The configuration of the vortex still remains cone-shaped until 100 degrees. Around 110 degrees the vortex system becomes unstable. Over 120 degrees, the rotational radius of the vortex increases and the configuration of the vortex begins to shift from cone-shaped to elliptical. That is, the vortex generated behind the leading edge changed from the longitudinal vortex system to the transverse vortex system whose rotating axis is vertical to the mean flow direction. It follows, therefore, that the longitudinal vortex can remain until the tip angle of 100 degrees, and going through the transient region around 110 degrees, the longitudinal vortex has been changed to the transverse vortex over 120 degrees. Figure 7(b) shows equi-contour lines of pressure coefficients. The definition of the pressure coefficient Cp is described in Equation (3) where Pm is the pressure on the wing surface and P∞ is the static pressure in the uniform flow speed U∞.
(3)
Cp coefficients show how the pressure on the wing behaves, compared with the pressure in the uniform fluid flow. It, therefore, follows that if Cp has negative value, the pressure on the wing surface is lower than that in the uniform flows. The characteristics of the longitudinal vortex are well reflected by pressure coefficients on the wing surface. The fast flows close to the wing tip are rapidly separated, but the rotational radius is small. Since the centrifugal force has the property that it is proportional to the square of the velocity and is in inverse proportion to the rotational radius, this causes the tip of the longitudinal vortex to induce the largest negative pressure. As a result, the wing tip has the lowest pressure coefficients in dark green color for θ = 90 and 110 degrees as shown in Figure 7(b). The pressures in the longitudinal vortex gradually tend to recover due to the diffusion of the vorticity and convection of flows. The characteristics of equi-contour lines of pressure coefficients agree well with the experimental results of actual vehicle by Ogawa [13] [14] especially for θ = 90 degrees. During the state of the longitudinal vortex system, the particles in the system will be accelerated until the velocities of the particles are faster than mean flow velocity. This makes pressure on the wing surface lower than that in the mean flow, and much lower than that in the mean flow particularly for θ = 90 degrees.
On the other hand, although the transverse vortex system is larger in spatial scale, the velocities of the particles are much slower than those of the particles in the longitudinal system. The numerical results agree well with the experimental ones obtained by flow visualization with the hydrogen bubble method in the running water channel. Due to the slow velocity of the fluid particles, the transverse vortex system causes smaller negative pressure on the wing surface, compared with the longitudinal system.
4.2. Vorticity Differences between the Longitudinal and the Transverse Vortex System
Although it is of great importance to investigate the relationships between the vorticity and the unsteady movement of the vortex systems in terms of aerodynamic sound generation, the characteristics of the longitudinal and the transverse vortex system were, as our first step, investigated to clarify the relationships between the typical vortex systems and the vorticity in detail. The vorticity of the longitudinal and the transverse vortex system were calculated for tip angles of the wing model with 40, 90, 110, 120, 130, and 140 degrees just as investigated in streamlines and Cp distributions. The vorticity will be described in Equation (4) to Equation (8) with respect to
the X, Y, Z coordinate axes and velocity vector![]()
. Three components![]()
, ![]()
, and ![]()
express the vorticity in the X, Y, Z axial directions respectively, and ![]()
expresses the magnitude of the vorticity.
![]()
(4)
![]()
(5)
![]()
(6)
![]()
(7)
![]()
(8)
Figure 8 shows the relationship between vorticity and tip angles in each section of A, B, and C for the tip angles of the wings 40, 90, 110, 120, 130, and 140 degrees. Of the three sections, the section A near the tip angle has by far the strongest vorticity in terms of magnitude of vorticity![]()
. In each section three quantities (![]()
, ![]()
,![]()
) fluctuate sharply whereas ![]()
remains almost constant. In particular, the component ![]()
which rotates on the X axis in the mean flow direction decreases rapidly between 110 degrees and 120 degrees in section A. On the other hand the ![]()
rotating on the Y axis increase until 110 degrees at which the ![]()
becomes almost equivalent to the ![]()
in both section A and B. Over 120 degrees, however, the ![]()
becomes much greater than the![]()
, and increase in all the sections. The ![]()
greatly decrease at 120 degrees due to the large decrease of the![]()
. Over 120 degrees, ![]()
begins to increase again due to increase of the![]()
. The longitudinal vortex can still remain until the tip angle of 110 degrees. However, between 110 degrees and 120 degrees the longitudinal characteristics become unstable. Over 120 degrees the characteristics of the vortex are considered to have been converted from the longitudinal to the transverse one. It is, therefore, found that the vorticity of the longitudinal vortex tends to be stronger than that of transverse vortex in terms of magnitude of the vorticity![]()
, although the governed component of the vorticity shifts from ![]()
to![]()
.
5. Experimental Measurement of Aerodynamic Noise
5.1. Low-Noise Wind Tunnel Test
The measurements of aerodynamic sound radiated from the delta wings with tip angles of 40, 90, 110, 120, 130, and 140 degrees were conducted at the wind flow velocity of 10, 20, 30, and 40 m/s in the low-noise wind tunnel of Kyushu University. Figure 9 shows the measurements of aerodynamic sound radiated from the delta wings and background noise without delta wings. Aerodynamic sound was measured at the position where a microphone was set at the same height as the delta wings 1.5 m away in the direction vertical to the delta wing as shown in Figure 10. The delta wings were set with 15 degrees of angles of attack just as in the flow visualization experiment and the numerical simulation for streamlines and vorticity.
5.2. Measuring Techniques
The microphone used is NL-52 of RIONCo., which can measure the sound with the frequency ranging 20 to 20,000 Hz. The measured aerodynamic sound was sent to the personal computer by means of a data-logger; NR-500 and a measuring unit; NR-HV04 of KEYENCE Co. All the data of aerodynamic sound were measured in the form of Z characteristics without any filter. Sampling frequency is 20 kHz and number of data are 400,000. To avoid frequency aliasing, digital sampling of the signal must be performed at least twice as rapidly as the highest frequency expected. This critical sampling rate is known as the Nyquist frequency. Therefore Nyquist frequency is 10 kHz in this test.
6. Experimental Results and Discussion
Aerodynamic sound measured in the far field is defined as Sound Pressure Level; SPL (dB) in Equation (9), where p is RMS of sound pressure measured 1.5 m away from the delta wing by the microphone, and p0 is
![]()
![]()
(a) (b)
Figure 9. Measurement of aerodynamic sound radiated from the delta wings in low-noise wind tunnel. (a) Measure- ments of aerodynamic sound; (b) Measurements of background noise without delta wings.
![]()
Figure 10. Setup of measurement of aerodynamic sound.
reference sound pressure; ![]()
![]()
(9)
Fast Fourier Transform (FFT) analyses were conducted under the condition that Hann window was used as window function with 50 blocks for data numbers of 400,000, overlapping coefficients 50%, numbers of arithmetic mean 99, and frequency resolution 2.5 Hz.
Figure 11 shows sound pressure level radiated from the delta wings for 4 airflow velocities with 6 tip angles of the wings. Aerodynamic sound is associated with frequency obtained by FFT analysis under the condition mentioned above. The study focuses on the frequency range from 200 to 5000 Hz where typical aerodynamic sound is captured, taking Nyquist frequency 10 kHz into consideration. The FFT results are processed by high- pass filter of 200 Hz and low-pass filter of 5000 Hz. In Figure 11 there exists a prominent frequency region with sound pressures which are larger than the background noise without wings shown in black color for each airflow
velocity. This prominent frequency region is considered to be aerodynamic sound radiated from the vortex systems behind the leading edge of the delta wings. Focuses are, therefore, put on the sound pressure level of the prominent frequency region. Since it is well known that human ear is the most sensitive in frequency band between 2000 to 4000 Hz, attention is paid to the prominent frequency band f from 2900 to 4000 Hz for the airflow velocity of 40 m/s. Generally speaking, the frequency f of shedding vortices from a bluff body is proportional to flow velocity U and inversely proportional to representative length of the body L, using Strouhal number St. The relationship is described as follows.
![]()
(10)
In the study, frequency band f was chosen as standard values of f = 2900 - 4000 Hz at U = 40 m/s. Since the frequency of shedding vortices is proportional to the airflow velocity in accordance with Equation (10), frequency bands are set as 0.25f = 725 - 1000 Hz at 0.25U = 10 m/s, 0.5f = 1450 - 2000 Hz at 0.5U = 20 m/s, and 0.75f = 2175 - 3000 Hz at 075U = 30 m/s. These chosen frequency bands are depicted in red-colored zone in Figure 11. Since the red-colored zone covers the prominent frequency band at the respective airflow velocity, it follows that measurements of aerodynamic sound are quite reasonable. With respect to aerodynamic sound obtained by FFT analyses, it is found that aerodynamic sound for the longitudinal vortex system with both red- colored line of θ = 40 degrees and green-colored line of θ = 90 degrees are larger than that for the transverse vortex system with other four colored lines.
Next step is to investigate the dependence of both aerodynamic sound produced by the longitudinal and the transverse vortex system on the airflow velocity. Aerodynamic sound is evaluated in the form of overall values SPLOA given by summing up sound pressure level Li of the frequency band in the red-colored zone for the respective airflow velocity, based on Equation (11).
![]()
(11)
The purpose of our research is to clarify not only the characteristics of aerodynamic sound but also generation mechanism of aerodynamic sound produced by the longitudinal and the transverse vortex system. As our first step, the characteristics of aerodynamic sound will be studied in the present paper. According to Equation (11), sound pressure levels were calculated for six delta wings and for mean airflow speeds as shown in Figure 12. It is found that the characteristics of aerodynamic noise radiated from the longitudinal and the transverse vortex
![]()
Figure 12. Relationships between aerodynamic sound and mean airflow velocities.
system increases in proportion to the 5th to the 6th power of mean airflow speeds, and that aerodynamic noise radiated from the longitudinal vortex system is greater than that from the transverse vortex system.
So far the two vortex systems have been investigated in terms of the configurations, vorticity, pressure coefficients on the wing surface, and aerodynamic noise experimentally and numerically. From now on, focuses are put on the generation mechanism of the aerodynamic noise from standpoints of the theoretical phase. As it is well known, Lighthill’s equation is described as Equation (12),
![]()
(12)
![]()
(13)
where Tij is Lighthill stress tensor, ρvivj: Reynolds stress.
The problem of calculating the turbulence generated sound is therefore equivalent to solving this equation for the radiation into a stationary, ideal fluid produced by a distribution of quadrupole sources whose strength per unit volume is the Lighthill stress tensor Tij.
The formal solution of Lighthill’s equation is given as
![]()
(14)
In the study, the mean density and sound speed are considered to be uniform throughout the fluid and the variations in the density ρ within a low Mach number, high Reynolds number source flow are then of order ρ0M2.
Therefore,![]()
. Similarly, if ![]()
is the local speed of sound in the source
region, it may also be shown that![]()
, so that
![]()
(15)
Thus, if viscous dissipation is neglected we make the approximation, provided that ![]()
![]()
(16)
The far-field acoustic pressure ![]()
in the far field is given by Equations (17) and (18), if Reynolds stress is known.
![]()
(17)
![]()
(18)
According to Howe [3] [4] , this equation is expressed in the form of the vorticity ![]()
as follows in terms of dipole source of the vorticity. This means that this equation is given by neglecting the retarded time caused by the difference of the place of the source in the source region due to the effects of the dipole from the quadrupole sound source
![]()
(19)
It therefore follows that since aerodynamic sound in the far field can be expressed as a function of the vorticity instead of the Reynolds stress, the vorticity plays a crucial role in generating aerodynamic sound. Equation (19) involves a double time rate of change. This implies that the vortices which change rapidly in time give great contributions to generating aerodynamic sound.
Curle [3] has derived a formal solution of Lighthill’s equation for the sound produced by turbulence in the vicinity of a solid body. The contribution to the dipole sound pressure pd from a surface element of diameter ![]()
within which the turbulence pressure fluctuations are correlated is evidently of order
![]()
(20)
which exceeds by an order of magnitude (![]()
) the sound pressure produced by a quadrupole in V of length scale![]()
. If A is the total surface area wetted by the turbulent flow, there are ![]()
independently radiating surface elements, and the total power Πd radiated by the dipole is proportional to the sixth power of airflow velocity.
![]()
(21)
This equation indicates that total power radiated by the dipole sound source increase in proportion to the sixth power of the mean airflow velocity. The direct power Πq radiated by quadrupole occupying a volume V0 in the absence of the body is given as in Equation (22). This is Lighthill’s eighth power law.
![]()
(22)
The sound produced by the turbulence near solid body S is therefore dominated by the dipole since M is nearly equivalent to 0.01 in this study, and as M approaches zero the acoustic power exceeds the quadrupole by a factor![]()
. That is, ratio of the dipole to the quadrupole is described as Equation (23)
![]()
(23)
Precisely how small M should be for this to be true depends on the details of the flow, which determine the approximate values of A and![]()
. Curle’s theoretical results support, following Equation (21), the experimental results that aerodynamic noise radiated from the longitudinal and the transverse vortex system increases in proportion to the 5th to the 6th power of mean airflow speeds as shown in Figure 12. The surface dipole represents the production of sound by the unsteady surface force that the body exerts on the exterior fluid. This increase in acoustic efficient brought about by surface dipoles on acoustically compact body occurs also for arbitrary, noncompact bodies when turbulence interacts with compact structural elements, such as edges, corners, and protuberances.
How [3] [4] derives the following vortex sound equation for the small Mach number
![]()
(24)
In the far field the acoustic pressure is given by the linearized approximation
![]()
(25)
where ![]()
is the total enthalpy.
The contribution to the sound from surface friction if normally of order
![]()
(26)
relative to the contribution from the volume vorticity, where ![]()
is the characteristic length scale of the turbulence or body and v is a typical velocity. At high Reynolds numbers the surface term can therefore be discarded, and in the present case in which the body does not vibrate, the acoustic far field is then given with the Green’s function ![]()
by
![]()
(27)
The next step of our study is, by means of the above vortex sound equation, to simplify this specific aerodynamic noise problem to obtain a thorough understanding of how the longitudinal and the transverse vortex system is produced, and how the noise can be estimated quantitatively.
7. Conclusions
Flows around the front pillar of an automobile are typical of a flow field with separated and reattached flow by a vortex system. It is known that the vortex system causes the greatest aerodynamic sound around a vehicle. The objective of the present study is to clarify the relationship between vortical structures and aerodynamic sound by the vortex system generated around the front pillar. The effects of the slant angles of the front pillars on the generation of the vortex systems were investigated by changing tip angles of the wings. The separation vortices behind the pillars generate the organized vortex systems, depending on the slant angles of the front pillars. The typical flows are reproduced by the three dimensional delta wings under the condition of low Mach numbers and high Reynolds numbers. The vortex systems were essentially reproduced by three-dimensional delta wings which consist of the longitudinal and the transverse system. The characteristics of the longitudinal vortex system were investigated in comparison with the transverse system. The results obtained are as follows.
1) The flow visualization experiment and the computational fluid dynamics (CFD) captured well the characteristics of the flow structure of the two vortex systems. These results showed that the longitudinal with the rotating axis along mean flow direction had cone-shaped configuration whereas the transverse with the rotating axis vertical to mean flow direction had elliptic one. Increasing the tip angles of the wings from 40 to 140 degrees, there first exists the longitudinal vortex system less than 110 degrees, with the transition region ranging from 110 to 120 degrees, and finally over 120 degrees the transverse vortex system appears.
2) The longitudinal vortex system with small tip angles of the wings less than 90 degrees has much faster streamlines due to the shape of the delta wing than those of the transverse one. The fast airflows cause the pressure on the wing surface to be much larger negative pressures, compared with those of the mean flow speeds. In the magnitude of the vorticity, the longitudinal vortex has much greater than the transverse vortex. The rotational velocity and vorticity have their largest values at the tip of the vortex and reduce downstream along the vortical axis. This resulted in inducing the largest negative pressure at the tip of the delta wing surface. Due to the slow velocity of the fluid particles, the transverse vortex system causes smaller negative pressure on the wing surface, compared with the longitudinal system.
3) The characteristics of aerodynamic sound radiated from the two vortex systems were investigated in low Mach number flows at high Reynolds numbers in the low-noise wind tunnel. As a result, it was found that the aerodynamic sound radiated from both the longitudinal and the transverse vortex system was proportional to the fifth from sixth power of mean flow velocity. The results almost agree with Curle’s dipole prediction.
4) The longitudinal vortex generates the aerodynamic sound larger than the transverse vortex system. This might be due to the fact that the vortex sound generation source div(ω×v) in the longitudinal vortex probably is larger than that in the transverse vortex system, as is the case with the comparison of steady vorticity for two vortex systems.
Nomenclature
Re: Reynolds Number
U: Flow Velocity (m/s)
L: Representative Length (m)
ν: Kinematic Viscosity (m2/s)
ω: Vorticity (1/s)
θ: Tip Angle of the Delta Wing (degree)
Cpt: Total Pressure Coefficient
Cp: Pressure Coefficient
Pm: Pressure of Measuring Point on the Wing (Pa)
P∞: Pressure in the Uniform Flow (Pa)
ρ: Density of Fluid (kg/m3)
SPL: Sound Pressure Level (dB)
f: Frequency
Tij: Lighthill Stress Tensor
ρvivj: Reynolds Stress
M: Mach Number
Πd : Total PowerRadiated by the Dipole
Πq: Total Power Radiated by the Quadrupole
G(x,y, t-τ): Green’s Function
![]()
Submit your manuscript at: http://papersubmission.scirp.org/