Some Integral Type Fixed Point Theorems in Dislocated Metric Space ()
Received 6 April 2016; accepted 6 June 2016; published 9 June 2016

1. Introduction
In 1986, S. G. Matthews [2] introduced some concepts of metric domains in the context of domain theory. In 2000, P. Hitzler and A.K. Seda [3] introduced the concept of dislocated topology where the initiation of dis- located metric space was appeared. Since then, many authors have established fixed point theorems in dislocated metric space. In the literature, one can find many interesting recent articles in the field of dislocated metric space (see for examples [4] - [10] ).
The study of fixed point theorems of mappings satisfying contractive conditions of integral type has been a very interesting field of research activity after the establishment of a theorem by A. Branciari [11] . The purpose of this article is to establish a common fixed point theorem for two pairs weakly compatible mappings with E. A. property and to generalize a result of B.E. Rhoades [1] in dislocated metric space.
2. Preliminaries
We start with the following definitions, lemmas and theorems.
Definition 1 [3] Let X be a non empty set and let 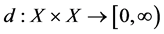 be a function satisfying the following conditions:
be a function satisfying the following conditions:
1. 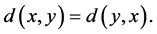
2. 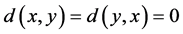 implies
implies 
3. 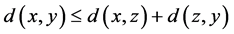 for all
for all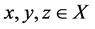 .
.
Then d is called dislocated metric (or d-metric) on X and the pair 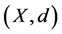 is called the dislocated metric space (or d-metric space).
is called the dislocated metric space (or d-metric space).
Definition 2 [3] A sequence 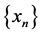 in a d-metric space
in a d-metric space 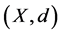 is called a Cauchy sequence if for given
is called a Cauchy sequence if for given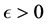 , there corresponds
, there corresponds 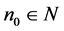 such that for all
such that for all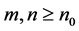 , we have
, we have .
.
Definition 3 [3] A sequence in d-metric space converges with respect to d (or in d) if there exists  such that
such that  as
as ![]()
Definition 4 [3] A d-metric space ![]() is called complete if every Cauchy sequence in it is convergent with respect to d.
is called complete if every Cauchy sequence in it is convergent with respect to d.
Lemma 1 [3] Limits in a d-metric space are unique.
Definition 5 Let A and S be two self mappings on a set X. If ![]() for some
for some![]() , then x is called coincidence point of A and S.
, then x is called coincidence point of A and S.
Definition 6 [12] Let A and S be mappings from a metric space ![]() into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is,
into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is, ![]() for some
for some ![]() implies
implies ![]()
Definition 7 [13] Let A and S be two self mappings defined on a metric space![]() . We say that the mappings A and S satisfy (E. A.) property if there exists a sequence
. We say that the mappings A and S satisfy (E. A.) property if there exists a sequence ![]() such that
such that
![]()
for some ![]()
3. Main Results
Now we establish a common fixed point theorem for two pairs of weakly compatible mappings using E. A. pro- perty.
Theorem 1 Let (X, d) be a dislocated metric space. Let ![]() satisfying the following con- ditions
satisfying the following con- ditions
![]() (1)
(1)
![]() (2)
(2)
where
![]()
is a Lebesgue integrable mapping which is summable, non-negative and such that
![]() (3)
(3)
![]() (4)
(4)
1. The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2. The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
if T(X) is closed then
1) the maps A and T have a coincidence point.
2 the maps B and S have a coincidence point.
3) the maps A, B, S and T have an unique common fixed point.
Proof. Assume that the pair ![]() satisfy E.A. property, so there exists a sequence
satisfy E.A. property, so there exists a sequence ![]() such that
such that
![]() (5)
(5)
for some![]() . Since
. Since![]() , so there exists a sequence
, so there exists a sequence ![]() such that
such that![]() . Hence,
. Hence,
![]() (6)
(6)
From condition (2) we have
![]() (7)
(7)
where
![]()
Taking limit as ![]() we get
we get
![]() (8)
(8)
Since
![]()
![]()
Hence we have
![]()
which is a contradiction, since![]() . Hence,
. Hence,![]() . Now we have
. Now we have
![]()
Assume ![]() is closed, then there exits
is closed, then there exits ![]() such that
such that![]() . We claim that
. We claim that![]() . Now from condition (2)
. Now from condition (2)
![]() (9)
(9)
where
![]()
Since
![]()
![]()
So, taking limit as ![]() in (9), We conclude that
in (9), We conclude that
![]() (10)
(10)
which is a contradiction. Hence![]() . Now we have
. Now we have
![]() (11)
(11)
This proves that v is the coincidence point of![]() .
.
Again, since ![]() so there exists
so there exists ![]() such that
such that
![]()
Now we claim that![]() . From condition (2)
. From condition (2)
![]()
where
![]()
Since
![]()
So if ![]() or
or ![]() we get the contradiction, since
we get the contradiction, since
![]()
or
![]()
Hence, ![]()
Therefore,![]() .
.
This represents that w is the coincidence point of the maps B and S.
Hence,
![]()
Since the pairs ![]() and
and ![]() are weakly compatible so,
are weakly compatible so,
![]()
![]()
We claim![]() . From condition (2)
. From condition (2)
![]()
where
![]()
Since
![]()
So if ![]() or
or ![]() or
or ![]() we get the contradiction. Since,
we get the contradiction. Since,
![]()
or
![]()
Hence, ![]()
Therefore,![]() . Similary,
. Similary,![]() . Hence,
. Hence,![]() . This represents that
. This represents that ![]() is the common fixed point of the mappings
is the common fixed point of the mappings ![]() and T.
and T.
Uniqueness:
If possible, let ![]() be other common fixed point of the mappings, then by the condition (2)
be other common fixed point of the mappings, then by the condition (2)
![]() (12)
(12)
where
![]()
Since
![]()
So if ![]() or
or ![]() or
or ![]() we get the contradiction, since
we get the contradiction, since
![]()
or
![]()
or
![]()
Hence, ![]() This establishes the uniqueness of the common fixed point of four mappings.
This establishes the uniqueness of the common fixed point of four mappings.
Now we have the following corollaries:
If we take T = S in Theorem (1) the we obtain the following corollary
Corollary 1 Let (X,d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
is a Lebesgue integrable mapping which is summable, non-negative and such that
![]()
![]()
1. The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2. The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
if S(X) is closed then
1) the maps A and S have a coincidence point
2) the maps B and S have a coincidence point
3) the maps A, B and S have an unique common fixed point.
If we take B = A in Theorem (1) we obtain the following corollary.
Corollary 2 Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
is a Lebesgue integrable mapping which is summable, non-negative and such that
![]() (13)
(13)
![]()
1. The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2. The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
if T(X) is closed then
1) the maps A and T have a coincidence point.
2) the maps A and S have a coincidence point.
3) the maps A, S and T have an unique common fixed point.
If we take T = S and B = A in Theorem (1) then we obtain the following corollary
Corollary 3 Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
is a Lebesgue integrable mapping which is summable, non-negative and such that
![]()
![]()
1. The pairs ![]() satisfy E. A. property.
satisfy E. A. property.
2. The pair ![]() is weakly compatible.
is weakly compatible.
if S(X) is closed then maps A and S have a unique common fixed point.
If we put S = T = I (Identity map) then we obtain the following corollary.
Corollary 4 Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]() (14)
(14)
![]() (15)
(15)
where
![]()
is a Lebesgue integrable mapping which is summable, non-negative and such that
![]() (16)
(16)
![]() (17)
(17)
if the pair (A, B) satisfy E.A. property and are weakly compatible then the maps A and B have an unique common fixed point.
Remarks: Our result extends the result of [14] .
Now we establish a fixed point theorem which generalize Theorem (2) of B. E. Rhoades [1] .
Theorem 2 Let (X, d) be a complete dislocated metric space, ![]() ,
, ![]() be a mapping such
be a mapping such
that for each ![]()
![]() (18)
(18)
where
![]() (19)
(19)
and
![]()
is a lebesgue integrable mapping which is summable , non negative and such that
![]() (20)
(20)
for each![]() , then f has a unique fixed point
, then f has a unique fixed point![]() , moreover for each
, moreover for each ![]()
![]()
Proof. Let ![]() and define
and define ![]() , then from (18)
, then from (18)
![]() (21)
(21)
now by (19)
![]()
But,
![]()
and similarly we can obtain, ![]()
Hence ![]()
Therefore by (21)
![]()
Similarly we can obtain,
![]()
Hence
![]()
Now taking limit as ![]() we get
we get
![]() (22)
(22)
by (20)
![]()
Now we claim that ![]() is a Cauchy sequence.
is a Cauchy sequence.
If possible let ![]() is not a Cauchy sequence, then there exists a real number
is not a Cauchy sequence, then there exists a real number ![]() and subsequences
and subsequences ![]() and
and ![]() such that
such that ![]() and
and
![]() (23)
(23)
Using (19) we have,
![]() (24)
(24)
Now using (22)
![]() (25)
(25)
Since by triangle inequality and (23)
![]()
Hence
![]() (26)
(26)
and
![]()
![]() (27)
(27)
Similarly
![]() (28)
(28)
Hence, from (20), (23), (24), (25), (26), (27) and (28)
![]()
which is a contradiction. Hence ![]() is a Cauchy sequence. Hence there exists a point
is a Cauchy sequence. Hence there exists a point ![]() such that the sequence
such that the sequence ![]() and its subsequences converge to z.
and its subsequences converge to z.
From the condition (18)
![]()
Now taking limit as ![]() we obtain
we obtain
![]()
which implies
![]()
So from the relation (20) we obtain ![]()
Uniqueness:
Let z and w two fixed point fixed points of the function f.
Applying condition (19) we obtain
![]()
If maximum of the given expression in the set is ![]() then
then
![]()
which is a contradiction, since![]() . Similarly for other cases also we get the contradiction. Hence z = w. This completes the proof of the theorem.
. Similarly for other cases also we get the contradiction. Hence z = w. This completes the proof of the theorem.