Theoretical Investigation of Structural, Electronic, and Mechanical Properties of Two Dimensional C, Si, Ge, Sn ()
Received 29 April 2016; accepted 3 June 2016; published 7 June 2016

1. Introduction
Hard materials are always of scientific interest due to their significance in fundamental science and industrial applications. It is also a well known fact that the covalently bonded light elements like carbon, boron, silicon etc. are very hard due to its nature of bonding. The number of publications exposes the enormous amount of interest shown by the research community on the noteworthy properties of 2D structures. The need for miniaturization of electronic devices also calls for extensive research among the 2D nanostructures that has obtained maximum hold in materials science and condensed matter physics.
Graphene has been documented as one of the thinnest, strongest, and stiffest materials ever discovered with a wide range of applications. The advances in the study have served as the motivating factor towards the extension of study in other 2D materials like silicene, germanane and stenane. Among these 2D nanostructures, graphene is the perfect semi metal which exhibits zero band gap due to the presence of massless Dirac Fermions. The orbital overlap of pz orbitals is maximum in graphene and so the hopping strength.
The other 2D materials are found to be stable only with buckling; silicene is next to graphene among the group IV elements and has an additional advantage of integrating it into Si based electronics and hence in nanoelectronics [1] . Germanene is also an important material as it has compatibility with Si in the semiconductor industry. The material also has high carrier mobility and can be a potential candidate in high speed electronic devices [2] . Stenane has an advantage over graphene that it can conduct electricity without dissipating energy as heat as per the predictions made by Shou-Cheng Zhang [3] . As all the 2D materials are reported to have excellent electronic properties suitable for the electronic industry, a perfect analysis on the mechanical properties would help to engineer these materials with suitable substrates for potential applications in engineering science.
2. Computational Details
The 2D structures of single layer graphene, silicene, germane and stenane as shown in Figure 1 have been constructed. The calculations were performed using the Density Functional Theory [4] [5] with Generalized Gradient Approximation (Perdew Burke-Ernzerhof, GGA-PBE) [6] exchange correlation functional as implemented in Cambridge Sequential Total Energy Package (CASTEP) code [7] . Ultrasoft pseudopotential [8] was used to represent the ionic cores. The total energy minimization is done using convergence tests that include lattice relaxation, energy convergence and k convergence to obtain a stable structure in the ground state. The crystal structures were geometrically optimized using Broyden-Fletcher-Goldfarb-Shanno [BFGS] [9] method with fixed basis quality as in CASTEP. Total energy is converged to 1 × 10−7 eV and the forces per atom were reduced to 5 × 10−5 eV. The calculations were carried out in the irreducible Brillouin zone with 44 × 44 × 1 k point mesh Monkhorst-pack scheme [10] . Kinetic energy plane wave cut off is set at 350 eV for all 2D materials except graphene which has the value set at 700 eV. A finite strain is applied to the optimized structure and the elastic stiffness matrix is determined from the linear relationship (Hooke’s law) between the resultant stress and the applied strain, and the polycrystalline bulk modulus and shear modulus were thus derived from the Voigt approximation scheme.
3. Results and Discussion
3.1. Structure
The pristine form of the 2D structures under study other than graphene is not experimentally manufactured successfully. It was predicted that the monolayer hexagonal structure of tin cannot be stable in freestanding form, whereas its binary compounds SnC, SnSi, and SnGe are stable even in free-standing form. There are a few reports on the synthesis of single crystals of silicon nanocrystals by thermal crystallization [11] . Germanene nanoribbons have also been fabricated in situ on C and BN nanotubes by Han et al. [12] . Li et al. have reported the synthesis of germanene sheet by its fabrication on a Pt(111) surface [13] . However, the existence of these superstructures on different substrates has been reported by many [14] - [17] . The progress in synthesis techniques has limited the experimental outputs to support most of the theoretical predictions. So far, the available synthesis approaches in producing graphene analogous Group IV elemental materials have been limited to epitaxial growth supported by substrates which leads to the metastable nature of these elemental sheets [18] . This is because unlike graphene, the other 2D structures do not have van der Waals interaction between layers in their bulk phase.
The unit cell of these 2D structures consists of two atoms. The interlayer distance is made reasonably large to ensure that there is no interaction between the layers. The schematic view of all 2D materials is shown in Figure 1. Silicene, germanene, and stenane the 2D analogues of graphene are structurally different from graphene due
to the buckling distortions in the individual six membered rings. Hence they can be easily functionalized through chemical reactions [19] . The electronic properties of 2D materials highly depend on the structure and its bonding characteristics [20] . The sp2 hybridization between one s orbital and two p orbitals leads to the formation of σ bond between carbon atoms that are separated by 1.42 Å. The planar σ bond is responsible for the robustness of the lattice structure. The unhibridized pz orbital which is perpendicular to the planar structure, can bind covalently with neighbouring carbon atoms, leading to the formation of a π bond. The π bond is not involved in covalent planar σ bond in the case of graphene [21] . Whereas the σ-π separation in other 2D structures reveals that the σ backbone gets stabilized and the π backbone is destabilized due to buckling. The π bonds in these structures are weaker than its counterpart in graphene and hence they tend to assume buckled structure [20] . The predictions made by the total energy calculations based on Density Functional theory also supports the fact that the planar structure is highly unstable, even though the structural and electronic properties of Si, Ge, and Sn resemble graphene.
The short range puckering seems to have pronounced effect in electronic properties. We find that it produces enormous effect in mechanical properties as well. The calculated total energies 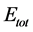 and structural parameters of all four structures after structural relaxation are tabulated in Table 1. The values agree well with the reported values. The space group of graphene is perfect D6h and changes to C3V in all other 2D materials. This is because the six-fold rotational and two mirror plane symmetries are missing in all materials other than graphene [22] .
and structural parameters of all four structures after structural relaxation are tabulated in Table 1. The values agree well with the reported values. The space group of graphene is perfect D6h and changes to C3V in all other 2D materials. This is because the six-fold rotational and two mirror plane symmetries are missing in all materials other than graphene [22] .
Bond order gives the stability of a bond and graphene is reported to have the highest bond order and hence proves its stability in the 2D form [20] . Present values are found to be in good agreement with the already predicted values.
Mulliken population analysis is performed to analyse the bonding behaviour. The overlap population may be used to assess the covalent or ionic nature of a bond [30] . A high value of the bond population indicates a covalent bond, while a low value indicates an ionic bond. The bond population of all four materials is calculated and given in Table 2. From the values obtained, we can infer that graphene exhibits maximum covalency compared to other materials. This endorses the strong mechanical properties of graphene. Also we could infer that the bond population decreases as we move down the column which in turn indicates the decrease in the covalency of the bonding and is reflected in the energy density contour. This is also due to the buckling present in the lattice structure. Furthermore the atomic population in s orbital increases and p decreases as we move down from graphene to stenane. This clearly indicates the overlapping of s and p orbitals which in turn proves the interaction between the planar σ bond and the perpendicular π bond. The overlapping increases from silicene to stenane and is found to be maximum in stenane and hence it exhibits more of sp3 hybridization. The bond angle in stenane is 110˚ which is very much closer to the bond angle of sp3 hybridized orbitals, 109.5˚. This results in the weakening of π bond due to the 5 pz orbital. This leads to the localization of electrons and hence will lose its Dirac like massless nature. This is reflected in energy dispersion curve, density of states histogram, and charge density contours.
The formation enthalpy refers to the thermodynamic stability. Negative formation enthalpy means an exothermic process and lower formation energy indicates the stability with respect to the decomposition to elemental constituents [31] . The values in Table 2 predict that all the materials are energetically favourable at ground state due to their negative formation enthalpies.
3.2. Electronic Band Structure
The band structure is calculated along the high symmetry directions Г, M, K, Г in the first Brillouin zone. The electronic band structure of all the four is generic in nature and agrees reasonably well with that reported in the literature. The sp2 hybridization and the presence of pz orbitals perpendicular to the plane in graphene give rise to the Dirac cone at the Fermi energy. The electrons in pz orbitals behave like massless fermions. Whereas in the
![]()
Table 1. Lattice parameter (Å), total energy (eV), bond angle (˚), buckling distance (Å), bond length (Å), and bond order of all four structures.
![]()
Table 2. Atomic population and Bond population of all materials.
case of other 2D materials like silicene, germanene, and stenane the hybridization tend to change from sp2 to sp3 and results in the formation of sp2/sp3 mixed orbital due to buckling. Buckling reduces the overlap area of pz orbitals in turn increases the overlapping of pz orbitals with the planar σ orbitals. Eventually the free movement of electrons as in the case of graphene is reduced. The linearity observed in graphene slowly changes to quadratic with an infinitesimal gap along the K direction at the Fermi level in the electronic dispersion curve. Dirac-like electronic structures are also seen in silicene, germanene and stenane that has been predicted already [32] . Figure 2 elucidates that the bands due to 2 s, 2 px, and 2 py orbitals in valence bands are highly localized and do not contribute towards the electronic properties. The conduction is mainly due to the electrons in pz orbitals. Dirac point in the energy dispersion curve endorses the behaviour of electrons as massless Fermions and it explicitly shows zero band gap in the case of Graphene. In other 2D materials the mobility of the electrons is reduced and hence effective mass is increased. Due to which a small bang gap is generated in turn the linear behaviour of energy dispersion at the K point changes to quadratic.
The energy of the hybridized s orbital along Г direction is very low in the case of graphene and is around 20 eV. The energy is increased to −11 eV in silicene and germanene and to −9 eV in stenane. The energy of the pz orbital in graphene is around −8 eV whereas in silicene and germanene it lies between −3 eV and −4 eV, which is close to zero in stenane. The energy gap shows a decreasing trend along the Γ direction: 7 eV in graphene, 3 eV in silicene, 1 eV in germanene and 0.6 eV in stenane. This proves that the energy of the orbitals decreases as the ionic radius increases. These values are in perfect agreement with the reported results.
3.3. Density of States
The density of states histogram (Figure 3) shows that the hybridization between the s and p orbitals near the Fermi level is close to zero in the case of graphene. The electronic contribution is purely due to pz orbital which leads to the zero gap in energy dispersion curves, whereas the hybridization between s and p at different degrees is found to occur in all other 2D materials near the Fermi level. The σ orbitals of buckled atom (Sublattice 2) overlap with the pz orbitals of planar atoms (sublattice 1). Hence s states are found near the Fermi level. This reduces the free nature of electrons in the pz orbital as in the case of graphene and hence linearity at the Dirac point becomes quadratic with a small band gap. The peaks due to the hybridized states in the case of silicene, germanene and stanene are found to be stronger than the peaks due to unhybridized states of pz orbitals in graphene near the Fermi level. Hence we can infer that the electrons in silicene, germanene and stenane will be more localized than the electrons in graphene near the Fermi level. Therefore the strength of C-C bond of graphene is lesser than the Si-Si, Ge-Ge, and Sn-Sn bonds. The DOS curves of all four are generic in nature except stenane. It is noted that the Fermi level has p states in stenane. This may be because of the influence of electrons in d orbitals which is beyond the scope of this work as this is done using pseudo code where only valence electrons are considered for calculation. The absence of band gap in the neighbourhood of the Fermi Level indicates that all the four have semi metallic character. The valence band starting from zero up to ~4 eV is mainly due to pz electrons. The main contribution from s electrons to the valence band is only from above ~4 eV. The states at the Fermi level are from pz electrons in all four materials. Hence we can conclude that the metallic behaviour of the materials is due to the pz electrons. The 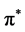 states dominate the bottom of the conduction bands ranging from zero to 10 eV in graphene, 6 eV in silicene, 4 eV in germanene and 4 eV in stenane. Besides the distribution from
states dominate the bottom of the conduction bands ranging from zero to 10 eV in graphene, 6 eV in silicene, 4 eV in germanene and 4 eV in stenane. Besides the distribution from  states there also exist some mixture of states due to the σ* states. The π* and σ* bands are split into several peaks: 8 π* peaks and 6 σ* peaks in graphene, 10 π* peaks and 9 σ* peaks in silicene, 12 π* peaks and 10 σ* peaks in germanene, 4 π* peaks and σ* peaks in silicene. In principle the energy difference between the peaks
states there also exist some mixture of states due to the σ* states. The π* and σ* bands are split into several peaks: 8 π* peaks and 6 σ* peaks in graphene, 10 π* peaks and 9 σ* peaks in silicene, 12 π* peaks and 10 σ* peaks in germanene, 4 π* peaks and σ* peaks in silicene. In principle the energy difference between the peaks
![]()
Figure 2. Electronic band structure of (a) graphene, (b) silicene, (c) germanene, (d) stenane. Orbital colours: 1st sp2 orbital (red), 2nd sp2 orbital (green), 3rd sp2 orbital (blue), unhybridized pz orbital (pink), π* orbital (cyan), σ* orbitals (yellow and dark magenta).
![]()
Figure 3. Density of states of (a) graphene, (b) silicene, (c) germanene, (d) stenane.
corresponds to the separation between the peaks in the K edges [33] . This would help us to analyse the possible excitations to the unoccupied orbitals that leads to the absorption spectra. Furthermore the pz orbitals at Fermi level in stanene shows reduced stability.
3.4. Charge Density Contours
Figure 4 depicts the electronic charge density of the upper valence bands of all four structures. In all four structures, the atoms are appeared to be covalently bonded. While in stenane the covalency seems to be decreased. Bonding between atoms also appears to be weaker compared to the other three structures. The charge distribution is found to be concentrated more at the core region which indicates more of ionicity. This is endorsed by our calculation of Poisson’s ratio which depicts stenane to be more ionic. May be this is the reason why the existence of freestanding form of stenane still remains as a challenge. The variation of the intensity of the electron density from ionic core is represented by blue (lower end) and red (higher end). The electron density is high in graphene followed by germanene as predicted [2] . The free electrons in the pz orbital which are responsible for conduction in other 2D materials is low due to the overlap of sp2 hybridized orbital with the pz orbital. The puckering effect is also seen clearly in the electron density contour of silicene where the atoms in the raised sublattice are seen prominently than the atoms in the other sublattice. It is more visible in stenane that the puckered atoms are not seen in the charge density contour.
3.5. Mechanical Properties
The elastic constants indicate the response of materials to an externally applied stress and offer important information regarding the bonding characteristics, anisotropy and hardness etc. [31] . In CASTEP symmetry-depen- dent strain patterns of different amplitudes are applied to the ground state structure. The corresponding stress tensors are calculated after a re-optimization of internal structural parameters. The elastic stiffness coefficients
are calculated from the applied strain and the computed stress. The calculation involves second order derivatives of the total energy with respect to lattice distortion. Young’s modulus, Poisson’s ratio, Bulk modulus and Shear modulus are derived from the elastic stiffness tensor and is mentioned in the following sections. The Young’s modulus, bulk modulus and shear modulus of graphene are very high compared to silicene, Germanene and stenane.
Elastic constants are critical parameters for analysing the mechanical properties of any material. The second order elastic constants exhibit the linear elastic response. The higher (>2) order elastic constants are important to characterize the nonlinear elastic response. The unit cell construction is done with 3D model by keeping the interlayer distance sufficiently large along the z-direction to minimize the van der Waals interaction.
The five independent elastic constants for a hexagonal structure Cij are C11, C12, C13, C33, C44 and C66. These are based on symmetry. C11, C22, & C33 are uniaxial elastic constants. C44, C55, and C66 are shear elastic constants. The born stability criteria [33] for a hexagonal structure are given as![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . The third and fourth conditions due to the shear elastic constants in the Born stability criteria appear to fail because they are 2D structures. This also proves that the van der Waals interactions along the z axis are perfectly minimized due to the large vacuum distance. However from the uniaxial elastic constants we can conclude that the planar structures are mechanically stable under ambient conditions. The shear stress does not hold much interest in 2D structures and hence the third and fourth conditions could be ignored. The uniaxial elastic constant C33 along the z axis is found to be very small which shows that the interactions along the z axis is minimized and it behaves as a perfect 2D structure.
. The third and fourth conditions due to the shear elastic constants in the Born stability criteria appear to fail because they are 2D structures. This also proves that the van der Waals interactions along the z axis are perfectly minimized due to the large vacuum distance. However from the uniaxial elastic constants we can conclude that the planar structures are mechanically stable under ambient conditions. The shear stress does not hold much interest in 2D structures and hence the third and fourth conditions could be ignored. The uniaxial elastic constant C33 along the z axis is found to be very small which shows that the interactions along the z axis is minimized and it behaves as a perfect 2D structure.
Hence for 2D materials, the stress-strain relation can be expressed in matrix form [34] which involves only two independent elastic constants
![]()
Besides the formation enthalpies, the elastic constants also endorse that they are mechanically stable.
The relationship between 3D elastic constants and 2D tension coefficients [35] are![]() ,
, ![]() ,
,![]() . Here
. Here ![]() represents the charge density and c is the distance along the z axis
represents the charge density and c is the distance along the z axis
between two layers. The in-plane Young’s modulus Ys and Poison’s ratio [25] are obtained from the following
relationships. ![]() and
and![]() .
.
The calculation of elastic constants shows that the Young’s modulus of graphene is 337 N/m along x-direction and y direction and agrees well with the already reported value of 340 N/m [36] . This indicates that the in-plane stiffness of graphene is highly isotropic along the x- and y-direction and weakens in all other materials. This suggests that graphene is highly incompressible along the in-plane direction. The calculated Young’s modulus of 340 N/m suggests that the material is very strong. The experimental value from chemically derived graphene is 250 GPa approximately 323 N/m [35] . The deviation observed in the values may be due to the impurity in the sample. The calculated elastic moduli are tabulated in Table 3.
Bulk modulus and shear modulus can also be obtained from the calculated elastic constants. Bulk modulus describes the resistance of a material to volume change and Shear modulus determines the resistance due to shape change. Three approximations are mainly used to obtain these values: Voigt, Reuss, and Hill. Voigt’s approach gives the upper bound of elastic properties in terms of uniform strain, the Reuss’s approach gives the lower bound in terms of uniform stress and Hill’s approach [37] gives an average between Voigt and Reuss. Here the calculations are done within the frame of Voigt Approximation.
Voigt Approximation [38]
![]()
![]()
Table 3. G/B values of graphene, silicene, germanene and stenane.
![]()
where ![]() gives the value of bulk modulus and
gives the value of bulk modulus and ![]() shear modulus. In all the four examined structures, the value of
shear modulus. In all the four examined structures, the value of ![]() is greater than
is greater than![]() . The bulk modulus describes the resistance towards change in shape against uniaxial tension [30] . The bulk modulus decreases as we move down the column from carbon to tin in 2D. Same is true for shear modulus. The overall mechanical moduli of graphene are very high compared to the other three.
. The bulk modulus describes the resistance towards change in shape against uniaxial tension [30] . The bulk modulus decreases as we move down the column from carbon to tin in 2D. Same is true for shear modulus. The overall mechanical moduli of graphene are very high compared to the other three.
The in plane stiffness of all the four is reported to decrease from graphene to stenane. The in-plane stiffness of Si, Ge, and Sn is 20%, 14% and 9% of that of graphene and can be explained with the help of bonding characteristics. In the periodic table Si, Ge, and Sn are found below C in the IV group and the bond length of all increases correspondingly from carbon. The atomic radius increases as we move down from carbon to tin and hence the bond length increases. Bond length increases from 1.42 (graphene) to 2.83 Å (stenane) in the present calculations and agree well with the reported values. This in turn reduces the bond strength. Bond length is inversely proportional to bond strength and the bond dissociation energy; a stronger bond will be shorter. Also all these structures form puckers in order to stabilize the honeycomb structure. This tends to the formation of sp3 hybridization results in a mixture of sp2/sp3 hybrid orbitals and hence weakens the π bond as against graphene. Thus the in-plane stiffness is lesser in all the structures other than graphene. Furthermore the electronegativity of carbon atoms is higher than all the other providing high mechanical strength to Graphene.
The ratio of shear to bulk modulus (![]() ) tabulated in Table 4 roughly gives an idea about the ductility of the material. The material is expected to be ductile when the G/B value is less than 0.5 and is brittle when it is greater than 0.5 [30] . From our results we infer that graphene and silicene are brittle in nature whereas germane and stenane exhibit ductility. It is in line with the results reported by material scientists from fracture toughness measurements that graphene is brittle in nature. The first systematic experimental analysis of elastic properties by Lee and co-workers also reveals the non-linear elastic behaviour and brittle fracture exhibited by graphene [36] .
) tabulated in Table 4 roughly gives an idea about the ductility of the material. The material is expected to be ductile when the G/B value is less than 0.5 and is brittle when it is greater than 0.5 [30] . From our results we infer that graphene and silicene are brittle in nature whereas germane and stenane exhibit ductility. It is in line with the results reported by material scientists from fracture toughness measurements that graphene is brittle in nature. The first systematic experimental analysis of elastic properties by Lee and co-workers also reveals the non-linear elastic behaviour and brittle fracture exhibited by graphene [36] .
Poisson’s ratio υ is associated with the volume change during the uniaxial deformation, which usually ranges from −1 to 0.5. The bigger the value of Poisson’s ratio, the better is the plasticity of the material. Typically, the value of υ is small for pure covalent materials (υ = 0.1), which is the case for graphene. The values are shown in Table 4. Besides G/B ratio, Poisson’s ratio also gives more insight into the brittle/ductile behaviour of materials. ![]() exhibits more of brittility. Graphene with
exhibits more of brittility. Graphene with ![]() shows covalent nature and increased brittleness. The value of υ for ionic and metallic materials is 0.25 and 0.33, respectively [42] . The covalent nature decreases from graphene to stenane and stenane shows typical metallic behaviour having
shows covalent nature and increased brittleness. The value of υ for ionic and metallic materials is 0.25 and 0.33, respectively [42] . The covalent nature decreases from graphene to stenane and stenane shows typical metallic behaviour having![]() , as materials with
, as materials with ![]() exhibit metallic behaviour. Silicene is between ionic and metallic whereas Germanene tends to be metallic [38] . It can be noticed that the Poisson ratio of silicene is about two times of graphene which is in perfect agreement with reports.
exhibit metallic behaviour. Silicene is between ionic and metallic whereas Germanene tends to be metallic [38] . It can be noticed that the Poisson ratio of silicene is about two times of graphene which is in perfect agreement with reports.
The hardness of materials is calculated using the expression![]() , given in Table 4, predicted by squared Pugh’s modulus ratio [45] . The results can give an insight into the hardness of the material as the calculation is meant for bulk materials. Our results display graphene to be the hardest compared to all other materials. It is because of the robustness of the covalent bonds between carbon atoms and also the construction is defect free, which might be an ideal condition. However predictions on graphene reveal that it is not the hardest material but is the strongest material and Diamond still owns the credit of being the hardest ever known.
, given in Table 4, predicted by squared Pugh’s modulus ratio [45] . The results can give an insight into the hardness of the material as the calculation is meant for bulk materials. Our results display graphene to be the hardest compared to all other materials. It is because of the robustness of the covalent bonds between carbon atoms and also the construction is defect free, which might be an ideal condition. However predictions on graphene reveal that it is not the hardest material but is the strongest material and Diamond still owns the credit of being the hardest ever known.
The elastic anisotropy of crystals is an important parameter for engineering science since it correlates the possibility of microcracks appearance in materials [41] [42] . The values of A1, A2 and A3 are equal to one for an
![]()
Table 4. G/B ratio, poisson ratio and hardness of graphene, silicene, germanene, and stenane.
![]()
Table 5. Values of A1, A2, and A3 of all materials.
isotropic crystal, while any value smaller or greater than one provides information on the degree of shear anisotropy possessed by the crystal [46] . The calculated results are listed in Table 5. It shows that the values of A1 and A2 are different for all four structures, while A1 = A2 ≠ A3. This is due to the crystal symmetry. The values of A3 equal to one for all structures indicate the isotropy on basal plane, which is consistent with the general feature of hexagonal close-packed structure.
Finally the strain energy per atom in-plane and out of plane is calculated considering compressions and tensions within the range −0.1 to +0.1. The strain energy per atom is calculated using the formula,![]() . Here
. Here ![]() is the energy of the strained system and
is the energy of the strained system and ![]() is the energy of the strain free system. n is the number of atoms in the unit cell. Figure 5 shows the strain energy per atom as a function of strain percentage in all the 2D materials. The strain energy per atom is found to be isotropic along the strain direction and symmetrical during compression and tension when uniaxial strain is applied along the x direction [25] . When the strain is applied along the other directions yz, zz, the strain energy per atom seems to be highly anisotropic along the strain directions and non symmetrical during compressions and tensions. Furthermore, the strain energy seems to remain almost constant in graphene whereas in other 2D materials it increases and decreases for certain strain percentage. This variation is attributed to the non uniform bond stretching between the planar atoms and the puckered atoms.
is the energy of the strain free system. n is the number of atoms in the unit cell. Figure 5 shows the strain energy per atom as a function of strain percentage in all the 2D materials. The strain energy per atom is found to be isotropic along the strain direction and symmetrical during compression and tension when uniaxial strain is applied along the x direction [25] . When the strain is applied along the other directions yz, zz, the strain energy per atom seems to be highly anisotropic along the strain directions and non symmetrical during compressions and tensions. Furthermore, the strain energy seems to remain almost constant in graphene whereas in other 2D materials it increases and decreases for certain strain percentage. This variation is attributed to the non uniform bond stretching between the planar atoms and the puckered atoms.
4. Conclusions
In summary, we have studied the structural stability and the electronic and mechanical properties of 2D nanostructures using DFT based First Principles Calculations. The structural analysis reveals that the sp2 hybridization occurs only in graphene. In all other materials hybridization tends to change from sp2 to sp3 due to buckling. The bond angle in stenane shows that the hybridization has almost become sp3. This buckling effect results in the weakening of π bond leading to a greater overlap between σ and π orbitals which in turn increases the bond energy. The buckling in the structure provides stability to form the hexagonal honeycomb structure in silicene, germanene and stenane. The negative values of formation enthalpy endorse the stable structural formation of all 2D structures under ambient conditions. However, the fabrication of free standing form of stenane still remains as a challenge to experimentalist. The electronic band structure calculations exhibits semimetallic behaviour of having zero band gap only for graphene. The other 2D structures under study posses an infinitesimal band gap at the K point due to the buckling in the structure.
The mechanical properties of all four 2D structures have been studied extensively. The strain energy per atom is isotropic along strain direction (along x). It is also symmetrical during tensile and compressive strains. This is not the same when strain is applied along other directions. This is due to the non-uniform stretching of bonds between the planar and raised sublattices which confirms the puckering in the structures. Graphene exhibits
![]() (a) (b)
(a) (b)
Figure 5. Strain energy per atom (a) strain applied along x direction, (b) strain applied along z and yz directions.
extreme mechanical properties compared to other 2D structures due to the pure covalent bonding between atoms. The in-plane stiffness is found to be very high for graphene whereas silicene, germanene and stenane have 20%, 14% and 9% graphene. Graphene and silicene are found to be brittle in nature, while germanene and stenane are ductile. Hence the latter two can be used extensively in semiconductor industry where substrates can add on to enhance the conduction properties. Crystal isotropy is observed in the basal plane of all four structures. This work concludes that not only graphene, other 2D structures: silicene, germanene, and stenane can also be used extensively in semiconductor and optical industries due to their similar structure and appreciable electronic and mechanical properties.
Acknowledgements
The computational facility offered by UGC-DAE Consortium of Indhira Gandhi Centre for Atomic Research is deeply acknowledged.