Received 6 April 2016; accepted 28 May 2016; published 31 May 2016

1. Introduction
Classical finite state automaton is the very basic model of classical finite machine. Likewise a quantum finite state automaton may be seen as basic model of finite state quantum machine. A variety of models of quantum finite state automaton are used. 1-way quantum finite automaton (1QFA) can be seen as the simplest model of quantum automaton .The two most popular models of quantum finite state automaton are quantum finite state automaton introduced by Moore and Crutchfield [1] (measure once quantum finite state automaton) and quan- tum finite state automaton introduced by Kondacs and Watrous [2] (measure many quantum finite state auto- maton). They have seemingly small difference, measure once quantum finite state automaton performs the mea- surement only at the end of computation,but for measure-many quantum finite state automaton the measure- ment will be performed by the automaton at every step of computation. Ambainis et al. [3] showed that measure many one-way quantum finite automata can accept all languages that can be accepted by measure once one-way quantum finite automata. Hence, in this paper,we consider the measure many quantum finite automata described by Kondacs et al. [2] . Whenever we mention one-way quantum finite automata we mean the model described by Konadacs et al. It has been shown by Kondacs et al. that the languages recognized by 1QFA’s form a proper subset of the regular languages. Besides these two models of QFA there are also such models of QFA as “enhanced” quantum finite state automaton [4] , latvian quantum finite state automaton [5] , 1-way QFA with control languages [6] , quantum finite state automaton with quantum and classical states (introduced by aharonov, kitaev and Nisan [7] ). Some other QFA models can be found in [8] [9] . In [10] , A. Nayek proposed a further generalization by allowing the QFA to perform several arbitrary measurements with intermediate unitary trans- formation at each step. The second model is 2-way quantum finite state automaton (2QFA) [2] . In this model,it is easy to simulate any deterministic automaton and some non-regular languages can be recognized as well; this implies that 2QFA’s are strictly more powerful than their classical counterparts. In [7] , they propose 2-way finite automaton with quantum and classical states, an intermediate model between 1QFA’s and 2QFA’s.
Languages accepted by multitape or multihead finite automaton were introduced in [11] and [12] . 1-way reversible and multihead finite automaton [13] and 2-way reversible multihead finite automaton [14] are in- troduced as a simple model of reversible computing and its language accepting capability is studied.
A konadacs and J Watrous [2] showed that 1QFA can only recognize regular languages,moreover, 1QFA cannot recognize all the regular languages. In [15] , they proposed a new model of one way QFA, namely, multiletter QFAs, that is an analogue of quantum automaton with classical memory containing the previously read letters. In these model,the automaton is not limited to seeing only one,the just incoming letter, but can see several earlier received letters as well. So a k-letter QFA is not limited to see only one,the just incoming input letter. Daowen Qiu et al. [16] further study the decidability of the equivalence and minimization problems of multiletter QFAs. In [17] , hierarchy and equivalence of multiletter quantum finite state automaton are studied.
Belovs et al. [15] have already showed that regular language 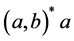 which can’t be accepted by 1QFA can be accepted by a 2-letter QFA.We continue the investigation of of 1-way quantum finite state automaton and k-letter quantum finite state automaton for improving their language accepting capabilities. In this paper, we introduce 1-way multihead quantum finite state automaton (1QFA(k)) by introducing multiple heads combined with existing automaton and study its language recognizing capabilities. It is proved that the newly introduced model 1QFA(2) can accept all unary regular languages.
which can’t be accepted by 1QFA can be accepted by a 2-letter QFA.We continue the investigation of of 1-way quantum finite state automaton and k-letter quantum finite state automaton for improving their language accepting capabilities. In this paper, we introduce 1-way multihead quantum finite state automaton (1QFA(k)) by introducing multiple heads combined with existing automaton and study its language recognizing capabilities. It is proved that the newly introduced model 1QFA(2) can accept all unary regular languages.
We know that the language  cannot be recognized by 1DFA(2) ( [18] [19] ) and
cannot be recognized by 1DFA(2) ( [18] [19] ) and
1RMFA(2) ( [13] ) respectively.Here we show that this language L can be recognized by our model 1QFA(k). It has been shown that 1QFA(2) is more powerful compare to 1RMFA(2) respectively.We consider the context- sensitive language: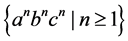 . It has been shown that this languages is also recognized by 1QFA(2).
. It has been shown that this languages is also recognized by 1QFA(2).
2. Preliminaries and Definitions
In this section we give different definitions and corresponding results for 1QFA.
2.1. Quantum Finite Automata
One-way quantum finite state automaton can been seen as the simplest model of quantum computation.Quantum finite automata could be of large importance is the fact that quantum memory seems to be very expensive and it is therefore of very much importance to know what can be achieved with limited amounts of quantum resources.
2.1.1. 1-Way Quantum Finite State Automata
One-way quantum finite state automaton seem to model very well the way very simple quantum processors work (Ambainis and freivalds, 1998), and also the way simple classical/quantum processors are expected to work: the classical part reads an input, picks up the corresponding quantum operator (a transition mapping) and performs it on a quantum memory of fixed size, independent of the size of input. 1QFA are very simple but less powerful than classical 1-way finite automaton.
Measure many quantum finite state automata (1QFA): We consider 1-way quantum finite automata (QFA) as defined in [2] .
Definition 1. Namely, a 1-way QFA is a tuple 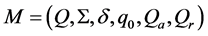 where
where
1) Q is a finite set of states,
2) 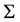 is an input alphabet,
is an input alphabet,
3) 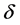 is a transition function,
is a transition function,
4) 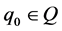 is a starting state,
is a starting state,
5) 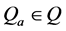 and
and 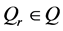 are sets of accepting and rejecting states.
are sets of accepting and rejecting states.
The states in 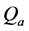 and
and 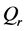 are called halting states and the states in
are called halting states and the states in 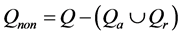 are called non- halting states.
are called non- halting states.  and
and 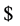 are symbols that do not belong to
are symbols that do not belong to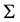 . We use
. We use ![]() and
and ![]() as the left and the right end marker, respectively. The working alphabet of M is
as the left and the right end marker, respectively. The working alphabet of M is![]() .
.
A superposition of M is any element of ![]() (the space of mappings from Q to
(the space of mappings from Q to ![]() with
with ![]() norm). For
norm). For![]() ,
, ![]() denotes the unit vector with value 1 at q and 0 elsewhere. All elements of
denotes the unit vector with value 1 at q and 0 elsewhere. All elements of ![]() can be expressed as linear combinations of vectors
can be expressed as linear combinations of vectors![]() . We will use
. We will use ![]() to denote elements of
to denote elements of![]() . The transition function
. The transition function ![]() maps
maps ![]() to C. The value
to C. The value ![]() is the amplitude of
is the amplitude of ![]() in the superposition of states to which M goes from
in the superposition of states to which M goes from ![]() after reading a. For
after reading a. For![]() ,
, ![]() is a linear transformation on
is a linear transformation on ![]() defined by
defined by
![]() (1)
(1)
The computation of a QFA starts in the superposition![]() . Then transformations corresponding to the left endmarker
. Then transformations corresponding to the left endmarker![]() , the letters of the input word x and the right endmarker
, the letters of the input word x and the right endmarker ![]() are applied. The transformation corresponding to a
are applied. The transformation corresponding to a ![]() consists of two steps. 1) First,
consists of two steps. 1) First, ![]() is applied. The new superposition
is applied. The new superposition ![]() is
is ![]() where
where ![]() is the superposition before this step. 2) Then
is the superposition before this step. 2) Then ![]() is observed with respect to the observable
is observed with respect to the observable ![]() where
where![]() ,
, ![]() ,
,![]() . This observation gives
. This observation gives![]() , with the probability equal to the amplitude of the projection of
, with the probability equal to the amplitude of the projection of![]() . After that, the superposition collapses to this peojection. If we get
. After that, the superposition collapses to this peojection. If we get![]() , the input is accepted. If we get
, the input is accepted. If we get![]() , the input is rejected. If we get
, the input is rejected. If we get![]() , the next transformation is applied.
, the next transformation is applied.
Theorem 1. Let L be any language recognized by 1QFA with bounded error. Then L is regular.
Proof. The proof is in [2] .
Proposition 1. Given a language![]() , it is not possible in general case to build a 1QFA that recognizes this language.
, it is not possible in general case to build a 1QFA that recognizes this language.
Proof. The proof is in [20] .
Theorem 2. The language ![]() a cannot be recognized by 1QFA with bounded error.
a cannot be recognized by 1QFA with bounded error.
Proof. This is shown in [2] .
2.1.2. 2-Way Quantum Finite State Automata
The model of 2-way quantum finite state automaton (2QFA) is first introduced by Watrous [2] . 2QFA is more powerful than their classical counterpart. A 2QFA consists of a finite state control and a 2-way tape head― which scans a read only input tape.
Definition 2. Formally, a 2-way QFA is specified by 6-tuplet ![]() where
where
1) Q is a finite set of states.
2) ![]() is an input alphabet.
is an input alphabet.
3) ![]() is a transition function which has a mapping of the form
is a transition function which has a mapping of the form![]() . In addition to input symbols
. In addition to input symbols![]() ,
, ![]() and
and ![]() are symbols that do not belong to
are symbols that do not belong to![]() . We use
. We use ![]() and
and ![]() as the left and the right end marker, respectively. The working alphabet of M is
as the left and the right end marker, respectively. The working alphabet of M is![]() .
.
4) ![]() is a starting state.
is a starting state.
5) ![]() are sets of accepting states.
are sets of accepting states.
6) ![]() are sets of rejecting states.
are sets of rejecting states.
The states in ![]() and
and ![]() are called halting states and the states in
are called halting states and the states in ![]() are called non- halting states.
are called non- halting states.
The 2QFA satisfies the following conditions (of well-formedness) for any![]() ,
, ![]() ,
,![]() :
:
1) Local probability and orthogonality condition
![]() .
.
2) Separability condition I
![]() .
.
3) Separability condition II
![]() .
.
4) Separability condition III
![]() .
.
In order to process an input word ![]() by M, we assume that the input is written on the tape with the endmarkers in the form wx = #x$ and such a tape of length |x| + 2 is circular, i.e., the symbol to the right of $ is #.
by M, we assume that the input is written on the tape with the endmarkers in the form wx = #x$ and such a tape of length |x| + 2 is circular, i.e., the symbol to the right of $ is #.
For an integer n let Cx be the set (of size (n + 2)|Q|) of all possible configuration of M, for inputs of length x. ![]() represents the amplitude with which a machine currently in state q and scanning symbol
represents the amplitude with which a machine currently in state q and scanning symbol ![]() will change state to
will change state to ![]() and move its tape head in direction d. For any tape
and move its tape head in direction d. For any tape ![]() induces an operator
induces an operator ![]() (called the time-evolution operator U on tape x) on
(called the time-evolution operator U on tape x) on ![]() as follows:
as follows:
![]() , k + d mod |x| for each
, k + d mod |x| for each ![]() and is extended to all
and is extended to all ![]() by
by
linearity. Consider the Hilbert space l2(Q), where Q is the set of internal states of a 2QFA M. Suppose that we havea linear operator ![]() for each
for each ![]() and a function D:
and a function D:![]() . Define tran- sition function
. Define tran- sition function ![]() as
as
![]()
and
![]()
M is well-formed when ![]() is unitary.
is unitary.
Theorem 3. Every regular language is accepted by a 2QFA.
Proof. The proof has been shown in [2] .
2.1.3. Multi-Letter Quantum Finite State Automata
Multi-letter quantum finite state automata has been introduced in [15] . In [16] , Qie etal. further study the decidability of the equivalence and minimization problems of multiletter QFAs. In [17] , hierarchy and equiva- lence of multiletter quantum finite state automaton are studied. k-letter QFA can be thought of as an analogue of quantum automata with classical memory containing the previously read letters. k-letter QFA is not limited to see only one, just incoming input letter, but can see several up to k of the earlier letter as well.
Definition 3. Formally, a k-letter QFA M is specified by a 5-tuple ![]() where
where
1) Q is a finite set of states,
2) ![]() are set of accepting states.
are set of accepting states.
3) ![]() is the initial quantum state from HQ.
is the initial quantum state from HQ.
4) ![]() is an input alphabet.
is an input alphabet.
5) ![]() is a transition function that assign a unitary trasition matrix
is a transition function that assign a unitary trasition matrix ![]() on
on ![]() to each string
to each string ![]()
and ![]() where Cn denotes Euclidean space consisting of all n-dimensional complex vectors.
where Cn denotes Euclidean space consisting of all n-dimensional complex vectors.
A k-letter QFA M works in the same way as an measure-once 1-way quantum finite state automaton [1] except that it applies unitary transformation corresponding not only to the last letter but to the last k-letters received. When k = 1, it is exactly same as measure once 1-way quantum finite state automaton. According to [16] , all languages accepted by k-letter QFAs with bounded error are regular language for any k.
To calculate the probability PM(x) that a k-letter QFA accepts an input string![]() , it fol-
, it fol-
lows that for any![]() ,
, ![]() is a unitary matrix. By
is a unitary matrix. By ![]() they define a map from
they define a map from ![]() to the set of
to the set of
of all ![]() unitary matrices.
unitary matrices. ![]() is induced by
is induced by ![]() in the following way. For
in the following way. For ![]()
![]()
and
![]()
which specifies the computing process of M for an input string x. They identify the states in Q with an orthonormal basis of the complex Euclidean space ![]() and let Pa denote the projection operator on the subspace spanned by Qa where
and let Pa denote the projection operator on the subspace spanned by Qa where
![]()
where ![]() denotes the conjugate transpose of vector
denotes the conjugate transpose of vector![]() .
.
3. Multihead Quantum Finite Automata
A k-head quantum finite automaton is a quantum finite automaton having a single read only input tape whose inscription is the input word in between two endmarkers. We define 1-way k-head QFA where k heads of the automaton can move to the right or stay on the current tape square but not beyond the endmarkers.
We show that 1QFA(2) is more powerful than 1RMFA(2).
3.1. 1-Way Multihead Quantum Finite State Automata (1QFA(k))
Definition 4. A 1-way multihead quantum finite state automaton is a automaton ![]() where
where
1) Q is a finite set of states,
2) ![]() are set of accepting states.
are set of accepting states.
3) ![]() is the initial quantum state superposition obeying normalization condition.
is the initial quantum state superposition obeying normalization condition.
4) ![]() is an input alphabet.
is an input alphabet.
5) ![]() is a transition function that assign a unitary trasition matrix
is a transition function that assign a unitary trasition matrix ![]() on
on ![]() to each string
to each string
![]() where Cn denotes Euclidean space consisting of all n-dimensional complex vectors. So
where Cn denotes Euclidean space consisting of all n-dimensional complex vectors. So ![]() is
is
a mapping of the form ![]() is the partial transition function where 1 means to move the head one square to the right and 0 means to keep the head at current square. We use # and $ as the left and the right end marker,respectively.
is the partial transition function where 1 means to move the head one square to the right and 0 means to keep the head at current square. We use # and $ as the left and the right end marker,respectively.
A superposition of M is any element in the Hilbert space l2(Q). For![]() ,
, ![]() denotes the unit vector with value 1 at q and 0 elsewhere. All elements of l2(Q) can be expressed as a linear combination of vectors.
denotes the unit vector with value 1 at q and 0 elsewhere. All elements of l2(Q) can be expressed as a linear combination of vectors.
The transition function ![]() maps
maps ![]() to
to ![]() where
where ![]() denotes the set of complex numbers. The value
denotes the set of complex numbers. The value ![]() is the amplitude of
is the amplitude of ![]() in the superposition of states to which M goes from
in the superposition of states to which M goes from ![]() after reading
after reading ![]() by 1st head,
by 1st head, ![]() by 2nd head and so on and moving the heads according to
by 2nd head and so on and moving the heads according to ![]() respectively. The head movement 0 denotes it stays in its position and 1 denotes head is moved to the right. For
respectively. The head movement 0 denotes it stays in its position and 1 denotes head is moved to the right. For ![]() is a linear transformation on l2(Q) defined by
is a linear transformation on l2(Q) defined by
![]()
We require all ![]() to be unitary. The check for wellformedness can be done in a similar manner as in [2] in the following way:
to be unitary. The check for wellformedness can be done in a similar manner as in [2] in the following way:
Consider the Hilbert space l2(Q), where Q is the set of internal states of a 1QFA(k) M. Suppose that we have a linear operator ![]() for each
for each ![]() and a function
and a function![]() . Define transition function
. Define transition function ![]() as:
as:
![]() (2)
(2)
and
![]() (3)
(3)
Here ![]() denotes the coefficient of
denotes the coefficient of ![]() in
in![]() . Eventually, M is well-formed if and only if
. Eventually, M is well-formed if and only if
![]()
and
![]()
for each ![]() pair. pair. The condition mentioned is similar to the condition for reversibility in [15] .
pair. pair. The condition mentioned is similar to the condition for reversibility in [15] .
The input word w begin with # and ends with $. The input is accepted if and only if the computation halts in an accepting states. It halts when the transition function is not defined for the current situation. In all other cases the input is rejected.
3.1.1. Matrices Representation of Different Automaton
In these section we write transition matrices of different automaton and discuss different properties of these automaton in terms of their transition matrices.
1) Deterministic finite state automaton
A deterministic finite automaton [20] consists of five tuple tuple ![]() where
where
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
3) ![]() is a transition function that takes as arguments a state and an input symbol and return a state,
is a transition function that takes as arguments a state and an input symbol and return a state,
4) ![]() is a starting state,
is a starting state,
5) ![]() is a set of final or accepting states.
is a set of final or accepting states.
We design a deterministic finite state automaton ![]() which accepts all of string having at least one alphabet “b” [see Figure 1] where
which accepts all of string having at least one alphabet “b” [see Figure 1] where
![]()
![]()
![]()
![]()
The transition matrix of the deterministic finite state automaton is shown in Figure 2.
Here each row of each transition matrix contain exactly one non-zero entry i.e. 1 for deterministic finite state automaton.
![]()
Figure 1. The deterministic finite state automaton accepts all length of string having at least one alphabet “b”.
![]()
Figure 2. The transition matrix of the deterministic finite state auto- maton accepts all length of string having at least one alphabet “b”.
2) Non-deterministic finite state automaton
An non-deterministic finite automaton [20] is represented essentially like a deterministic finite state auto- maton. It consists of five tuple ![]() where
where
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
3) ![]() is a transition function that takes a state in Q and an input symbol in
is a transition function that takes a state in Q and an input symbol in ![]() as arguments and returns a subset of Q,
as arguments and returns a subset of Q,
4) ![]() is a starting state,
is a starting state,
5) ![]() is a set of final or accepting states.
is a set of final or accepting states.
The only difference between an non-deterministic finite state automaton and deterministic finite state auto- maton is the value of ![]() that returns a set of states in the case of an non-deterministic finite state auto- matonand single state in the case of deterministic finite state automaton.We design a non-deterministic finite state automaton
that returns a set of states in the case of an non-deterministic finite state auto- matonand single state in the case of deterministic finite state automaton.We design a non-deterministic finite state automaton ![]() (shown in Figure 3) which accepts all of string having at least one alphabet “b” where
(shown in Figure 3) which accepts all of string having at least one alphabet “b” where
![]()
![]()
![]()
![]()
![]()
The transition matrix of the deterministic finite state automaton is shown in Figure 4.
There is atleast one row in a transition matrix for non-deterministic automaton which contain more than one non-zero entry.
3) Reversible finite state automaton
An automaton ![]() [21] is reversible if, for every state p in Q for every letter a in M there existsat most one transition in
[21] is reversible if, for every state p in Q for every letter a in M there existsat most one transition in ![]() that comes from p (respectively goes to p) with label a. Here
that comes from p (respectively goes to p) with label a. Here
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
3) ![]() is a transitions,is a subset of
is a transitions,is a subset of![]() ,
,
4) ![]() is a set of final states,
is a set of final states,
5) ![]() is a set of final states.
is a set of final states.
![]()
Figure 3. The non-deterministic finite state automaton accepts all length of string having at least onealphabet “b”.
![]()
Figure 4. The transition matrix of the non-deterministic finite state automaton accepts all length of string having at least one alphabet “b”.
A reversible automaton is a finite automaton in which each letter induces a partial one-to-one map from the set of states into itself. A reversible automaton may have several initial or final states. As a consequence, the minimal automaton of a reversible language may not reversible.
We define reversible automaton ![]() shown in Figure 5 which accept string of a’s of length 3 where
shown in Figure 5 which accept string of a’s of length 3 where
![]()
![]()
![]()
The transition matrix of the above automaton is shown in Figure 6.
In case of reversible automaton dot product of any two row is zero and there are no cycles within the transi- tion/output matrix that can’t accessed from one of the input states.
4) Probabilistic finite state automaton
A probabilistic finite state automaton [22] over the alphabet ![]() is a system consists of
is a system consists of ![]() where
where
1) Q is a finite set of states,
2) ![]() is a transition function from
is a transition function from ![]() into
into ![]() such that for
such that for![]() ,
, ![]() ,
, ![]() ,
, ![]()
3) ![]() is a starting state,
is a starting state,
4) ![]() is a set of final or accepting states.
is a set of final or accepting states.
In case of probabilistic finite state automaton we allow the fractional values in transition matrix with the provision that sum of each row give 1 [see Figure 7].
5) Quantum finite state automaton
We consider 1-way quantum finite state automata (QFA) as defined in [23] is a tuple ![]() where
where
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
![]()
Figure 5. The reversible automaton accept string of a’s of length 3.
![]()
Figure 6. The transition matrix of the reversible automaton accepts string of a’s of length of 3.
3) ![]() is a transition function,
is a transition function,
4) ![]() is a starting state
is a starting state
5) ![]() and
and ![]() are sets of accepting and rejecting states.
are sets of accepting and rejecting states.
The states in ![]() and
and ![]() are called halting states and the states in
are called halting states and the states in ![]() are called non- halting states.
are called non- halting states. ![]() and
and ![]() are symbols that do not belong to
are symbols that do not belong to![]() . We use
. We use ![]() and
and ![]() as the left and the right end marker, respectively. The working alphabet of M is
as the left and the right end marker, respectively. The working alphabet of M is![]() . Quantum finite state automaton is obtainby letting the transition matrix with complex entries.We also require each of the matrices to be unitary.
. Quantum finite state automaton is obtainby letting the transition matrix with complex entries.We also require each of the matrices to be unitary.
The transition matrix of the quantum finite state automaton looks like [Figure 8]:
The transition matrix is unitary since the sum of the squares of the norms in each row adds up to 1 and the dot product of any two row is 0.If all matrices only have 0 or 1 entries and the matrices are unitary,then the automaton is deterministic and reversible.
6) 1-way multihead deterministic finite state automaton
A 1-way k-head deterministic finite state automaton is a deterministic finite state automaton with k- independent read heads on a single input tape with the end markers. On each move the machine can si- multaneously read the k input cells scanned by k-heads,move each head one square to the right or keep stationary.
A 1-way multihead deterministic finite state automaton (1DFA(k)) [13] is a tuple ![]() where
where
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
3) ![]() is the number of heads.
is the number of heads.
4) ![]() is the partial transition function;where 1 means to move the head one square to the right and 0 means to keep the head on the current square,
is the partial transition function;where 1 means to move the head one square to the right and 0 means to keep the head on the current square,
5) ![]() is the left and
is the left and ![]() is the right endmarkers.
is the right endmarkers.
6) ![]() is a starting state,
is a starting state,
7) ![]() is a set of final or accepting states.
is a set of final or accepting states.
We define a 1DFA(2) ![]() shown in Figure 9 which accept
shown in Figure 9 which accept ![]() where
where
![]()
![]()
![]()
![]()
![]()
Figure 8. The transition matrix of the automaton contain complex entry.
![]()
Figure 9. 1DFA(2) accept a language ![]() labelover flow.
labelover flow.
The transition matrix of the above automaton is [see Figure 10].
Each row of transition matrix contain only one 1 which has the same property as deterministic finite state automaton.
7) 1-way Reversible multihead finite state automaton
A 1-way reversible multihead finite state automaton (1REV-DFA(k)) [13] is a tuple ![]() which has same structure as 1DFA(k) where
which has same structure as 1DFA(k) where
1) Q is a finite set of states,
2) ![]() is an input alphabet,
is an input alphabet,
3) ![]() is the number of heads.
is the number of heads.
4) ![]() is the partial transition function;where 1 means to move the head one
is the partial transition function;where 1 means to move the head one
square to the right and 0 means to keep the head on the current square,
5) ![]() is the left and
is the left and ![]() is the right endmarkers.
is the right endmarkers.
6) ![]() is a starting state,
is a starting state,
7) ![]() is a set of final or accepting states.
is a set of final or accepting states.
Let M be a 1DFA(k) and D be the set of all reachable configuration that occur in any computation of M beginning with an initial configuration and ![]() with
with![]() ,
, ![]() and
and![]() . D be the set of all reachable configurations that occur in any computation. M is said to be reversible if the following two conditions are fulfilled:
. D be the set of all reachable configurations that occur in any computation. M is said to be reversible if the following two conditions are fulfilled:
1) For any two transitions:
![]()
and
![]()
it holds if![]() .
.
2) There is at most one transition of the form
![]() .
.
The non-context free language ![]() is accepted by REV-1DFA(2)
is accepted by REV-1DFA(2)
![]() shown in Figure 11 where the transition function
shown in Figure 11 where the transition function ![]() is asfollows:
is asfollows:
![]()
Figure 10. The transition matrix of1DFA(2) accept a language![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The transition matrix of the above automaton is shown in Figure 12.
Dot product of any two row is zero for multihead reversible finite state automaton.
8) 1-way multihead quantum finite state automaton
1-way multihead quantum finite state automaton is a 1-way k-head quantum finite state automaton where k-heads of the automaton can move to the right or stay on the current tape square but not beyond the end markers.The language ![]() is accepted by the 1QFA(k)
is accepted by the 1QFA(k)
![]() [see Figure 13] where
[see Figure 13] where
![]()
![]()
![]()
Figure 12. The transition matrix of 1REV-DFA(2) accept a language![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The transition matrix of the above automaton is shown in Figure 14.
The sum of the square of the norms in each row adds up to 1 and dot product of any two row is zero formultihead quantum finite state automaton.
3.1.2. Recognition of Language Class
In this section we show that 1QFA(k) has more language recognizing power than 1QFA. 1QFA(2) can recognize regular language ![]() and context-sensitive language
and context-sensitive language ![]() respectively.
respectively.
Theorem 4. 1QFA(2) can accept all unary regular languages.
Proof. In [12] it has been shown that any unary regular language is accepted by some 1-way reversible 2-headdeterministic finite automaton. We find from the previous section that in a 1-way multihead quantum
![]()
Figure 13. 1QFA(2) accept a language ![]() with acceptance probability p > 0.
with acceptance probability p > 0.
![]()
Figure 14. The transition matrix of 1QFA(2) accept a language ![]() with acceptance probability p > 0.
with acceptance probability p > 0.
finitestate automaton where the transition matrices are only 0 and 1 entry, it is essentially a 1-way reversible multihead finite state automaton. So 1-way 2-head quantum finite state automaton accept all unary language.
Example 1. A 1-way 2-head quantum finite state automaton is a automaton ![]() can accept
can accept ![]() in the folowing manner:
in the folowing manner:
Let, ![]() ,
, ![]() ,
, ![]()
Define:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The automaton acts as follows: Initially both heads of the automaton M are at #. After reading the input symbols, the automaton M remain at state![]() . The first head remain stationary where the second head move one square to the right of the input tape whenever the automaton reaches at state
. The first head remain stationary where the second head move one square to the right of the input tape whenever the automaton reaches at state![]() . The movement of heads are similar as the previous case. Due to the movement of heads the second head may be at “a” or “b”.
. The movement of heads are similar as the previous case. Due to the movement of heads the second head may be at “a” or “b”.
For both cases the automaton M move to state ![]() from state
from state ![]() and both heads move one square to theright of the input tape. When the first head at “a” and second head at “$”, the automaton M goes to final state
and both heads move one square to theright of the input tape. When the first head at “a” and second head at “$”, the automaton M goes to final state ![]() from
from ![]() and the string will be accepted by the automaton M with probability 1.
and the string will be accepted by the automaton M with probability 1.
Consider a string w not in L. As w is not in L the heads of the automaton M will arrived in such a way that for that particular position of heads and state, no transition rules are defined. So, for a string w, which M does not accept, there is no sequence of transitions that makes M to its final state after consumption of w. So, M rejects with probability 1. Each pairs of ![]() is unitary.
is unitary.
Example 2. A 1-way 2-head quantum finite state automaton is a automaton ![]() can accept
can accept ![]() in the following manner:
in the following manner:
Let, ![]() ,
, ![]() ,
, ![]()
Define:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The automaton acts as follows: Initially both heads of the automaton M are at #. After reading the input symbols, the automaton M remains at ![]() and the first head remain stationary and the second head moveone square to the right of the input tape.Whenever the automaton M reach at state
and the first head remain stationary and the second head moveone square to the right of the input tape.Whenever the automaton M reach at state ![]() the movement of heads are similar as the above case.The automaton M performs similar task as previous one for all inputletter “a” until the next input letter read by second head is “b”. For reading input letter “b” by the second head of the automaton M, it moves to state
the movement of heads are similar as the above case.The automaton M performs similar task as previous one for all inputletter “a” until the next input letter read by second head is “b”. For reading input letter “b” by the second head of the automaton M, it moves to state ![]() and remains at state
and remains at state ![]() until the next input letter read by thesecond head is “c”. This steps counts the number of letter “b” with number of letter “a”. Both heads move one square to the right of the input string for state
until the next input letter read by thesecond head is “c”. This steps counts the number of letter “b” with number of letter “a”. Both heads move one square to the right of the input string for state![]() . After reading the letter “c” by second head where the first is reading letter “a” of the input string, the automaton M goes to state
. After reading the letter “c” by second head where the first is reading letter “a” of the input string, the automaton M goes to state ![]() from state
from state![]() . Both heads moveone square to the right of the input string whenever
. Both heads moveone square to the right of the input string whenever ![]() state will be reached. The automaton M now checks the number of letter “b” and “c” of the input string with two heads of the automaton until the second head readthe right endmarker $, for which the automaton goes to state
state will be reached. The automaton M now checks the number of letter “b” and “c” of the input string with two heads of the automaton until the second head readthe right endmarker $, for which the automaton goes to state![]() . When the automaton M is in state
. When the automaton M is in state ![]() and both heads read the right endmarker $, then the automaton accept the input string with probability 1.
and both heads read the right endmarker $, then the automaton accept the input string with probability 1.
Consider a string w not in L. As w is not in L the heads of the automaton M will arrived in such a way that for that particular position of heads and state, no transition rules are defined. So, for a string w, which M does not accept,there is no sequence of transitions that makes M to its final state after consumption of w. So, M rejects with probability 1. Condition of unitarity is satisfied for all pairs of![]() .
.
Theorem 5. 1QFA(2) is more powerful than 1QFA with respect to recognition of language.
Proof. In Theorem 2 it was proved that the language ![]() cannot be recognized by 1QFA with bounded error. In Example 1 we proved that it can be done with 1QFA(2).
cannot be recognized by 1QFA with bounded error. In Example 1 we proved that it can be done with 1QFA(2).
Theorem 6. Given a language ![]() it is possible in general case to build a 1QFA(k) that re- cognizes this language.
it is possible in general case to build a 1QFA(k) that re- cognizes this language.
Proof. In [24] it has been shown that this language consists of subset of words from ![]() language whichis recognize by 1QFA(2) as shown in Example 1.
language whichis recognize by 1QFA(2) as shown in Example 1.
Example 3. A 1-way 2-head quantum finite state automaton is a automaton ![]() can accept
can accept ![]() in the following manner:
in the following manner:
Let, ![]() ,
, ![]() ,
, ![]()
Define:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The automaton acts as follows: at each reading of the symbol ![]() the automaton goes into a super-
the automaton goes into a super-
position of two states ![]() and
and ![]() with amplitude a
with amplitude a ![]() respectively.This is done with the objective that at
respectively.This is done with the objective that at
each reading of the symbol the automaton guesses x to be the first character which does not match. Thus if the guess is rightthen the path corresponding to ![]() goes to an accepting states and the guess is wrong the path correspondingto
goes to an accepting states and the guess is wrong the path correspondingto ![]() goes to an rejecting state. Even if the guess is wrong the path corresponding to
goes to an rejecting state. Even if the guess is wrong the path corresponding to ![]() allows us to makeanother guess. So if the input word belongs to L and kth letter does not match with theend.
allows us to makeanother guess. So if the input word belongs to L and kth letter does not match with theend.
Then at the kth depth ![]() will reach an accepting states with probability
will reach an accepting states with probability![]() . But if the input word is an
. But if the input word is an
palindrome and does notbelong to L then no matter what depth we traversed ![]() will never go to an accepting state. As the aboveautomaton is 1-way and the length of the input word is finite, the above automaton will always halt in finitetime and the input string belonging to the language is accepted by the automaton if the probability of state
will never go to an accepting state. As the aboveautomaton is 1-way and the length of the input word is finite, the above automaton will always halt in finitetime and the input string belonging to the language is accepted by the automaton if the probability of state ![]() is greater than 0. We arrive at this conclusion because if the word is palindrome the probability of
is greater than 0. We arrive at this conclusion because if the word is palindrome the probability of ![]() will be 0. Each
will be 0. Each ![]() is unitary by inspection. So M is well-formed. Figure 15 and Figure 16 shown below describe the working steps of the automaton in pictorial form.
is unitary by inspection. So M is well-formed. Figure 15 and Figure 16 shown below describe the working steps of the automaton in pictorial form.
![]()
Figure 15. Input “abba” is palindrome and hence it is not accepted.
![]()
Figure 16. Input “abba” is not palindrome and hence it is accepted.
Theorem 7. ![]() where
where ![]() is the set of all languages accepted by 1-way 2-head quantum finite state automaton and
is the set of all languages accepted by 1-way 2-head quantum finite state automaton and ![]() is the set of all languages accepted by 1-way 2-headdeterministic finite state automaton.
is the set of all languages accepted by 1-way 2-headdeterministic finite state automaton.
Proof. The language ![]() cannot be recognized by 1DFA(2) ( [18] [19] ). In Example 3 we proved that it can be done with 1QFA(2).
cannot be recognized by 1DFA(2) ( [18] [19] ). In Example 3 we proved that it can be done with 1QFA(2).
Theorem 8. For every 1-way reversible 2-head finite state automaton M which accepts a language L, thereexists a 1-way 2-head quantum finite state automaton M’ which accepts the same language L.
Proof. We know that the transition matrix of 1-way reversible multihead finite state automaton has the following properties:
1) Dot product of any two row is zero for 1-way reversible multihead finite state automaton.
2) All matrices only have 0 or 1 entries.
Therefore the above two properties of the transition matrix ensures that the transition matrix is also unitary. As a result given a 1-way reversible 2-head finite state automaton M we get a 1-way 2-head quantum finite state automaton M’ which has the same transition matrix,same set of states, same set of accepting states and start state as M. as the transition matrix, start state and accepting states of M and M’ are same,they accept the same language.
Theorem 9. The set of all languages accepted by 1-way reversible 2-head finite state automata (1RMFA(2)) is a proper subset of set of all language accepted by 1-way 2-head quantum finite state automata. (1QFA(2))
Proof. Theorem 8 tells us that for every 1RMFA(2) which accept a language L there exist 1QFA(2) which accept the same language. So, the set of all languages accepted by 1RMFA(2) is a subset of set of all languages accepted by 1QFA(2). From ( [18] [19] ) we know that the language ![]() is not accepted by any 1DFA(2). Also from ( [13] ) we know that the set of all languages accepted by 1RMFA(2) is a proper subset of 1DFA(2). Therefore, there is no 1RMFA(2) which accepts the language
is not accepted by any 1DFA(2). Also from ( [13] ) we know that the set of all languages accepted by 1RMFA(2) is a proper subset of 1DFA(2). Therefore, there is no 1RMFA(2) which accepts the language![]() . In Example 3 ithas been shown 1QFA(2) accept the language L. Thus, the subset relation is proper.
. In Example 3 ithas been shown 1QFA(2) accept the language L. Thus, the subset relation is proper.
Corollary 1. 1QFA(2) is computationally more powerful than 1RMFA(2).
4. Conclusion
In this paper, we studied characteristics of 1QFA(k) with their language accepting capability. There are still many non-regular context free context sensitive languages accepted by 1QFA(k) other than shown in this paper. We show that ![]() where
where ![]() is the set of all languages accepted by 1-way 2-head quantum finite state automaton and
is the set of all languages accepted by 1-way 2-head quantum finite state automaton and ![]() is the set of all languages accepted by 1-way 2-head deterministic finite state automaton. We also show that 1QFA(2) is more powerful than 1RMFA(2) with respect to recognition of language. But though 1QFA(2) can accepts some non-regular languages but it is still not be proved that whether 1QFA(2) can accepts all regular languages.We can explore it by using the superposition property of 1QFA(k).
is the set of all languages accepted by 1-way 2-head deterministic finite state automaton. We also show that 1QFA(2) is more powerful than 1RMFA(2) with respect to recognition of language. But though 1QFA(2) can accepts some non-regular languages but it is still not be proved that whether 1QFA(2) can accepts all regular languages.We can explore it by using the superposition property of 1QFA(k).
Acknowledgements
Research of Debayan Ganguly is funded by the Council of Scientific Industrial Research (CSIR). This support is greatly appreciated.