
Received 18 March 2016; accepted 24 May 2016; published 27 May 2016

1. Introduction
Definition 1.1. Let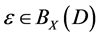 . If
. If  or
or 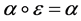 for any
for any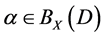 , then
, then 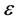 is called an idempotent element or called right unit of the semigroup
is called an idempotent element or called right unit of the semigroup 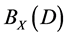 respectively.
respectively.
Definition 1.2. We say that a complete X-semilattice of unions D is an XI-semilattice of unions if it satisfies the following two conditions:
a)  for any
for any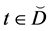 ;
;
b)  for any nonempty element Z of D (see [1] , Definition 1.14.2 or see [2] , Definition 1.14.2).
for any nonempty element Z of D (see [1] , Definition 1.14.2 or see [2] , Definition 1.14.2).
Definition 1.3. Let D be an arbitrary complete X-semilattice of unions,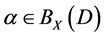 . If
. If
![]()
then it is obvious that any binary relation ![]() of a semigroup
of a semigroup ![]() can always be written in the form
can always be written in the form
![]() the sequel, such a representation of a binary relation
the sequel, such a representation of a binary relation ![]() will be called quasinormal.
will be called quasinormal.
Note that for a quasinormal representation of a binary relation![]() , not all sets
, not all sets ![]() can be different from an empty set. But for this representation the following conditions are always fulfilled:
can be different from an empty set. But for this representation the following conditions are always fulfilled:
a)![]() , for any
, for any ![]() and
and![]() ;
;
b) ![]() (see [1] , Definition 1.11 or see [2] , Definition 1.11).
(see [1] , Definition 1.11 or see [2] , Definition 1.11).
Theorem 1.1. Let D, ![]() ,
, ![]() and I denote respectively the complete X-semilattice of unions D, the set of all XI-subsemilattices of the semilattice D, the set of all right units of the semigroup
and I denote respectively the complete X-semilattice of unions D, the set of all XI-subsemilattices of the semilattice D, the set of all right units of the semigroup ![]()
![]() and the set of all idempotents of the semigroup
and the set of all idempotents of the semigroup![]() . Then for the sets
. Then for the sets ![]() and I the following statements are true:
and I the following statements are true:
a) if ![]() and
and![]() , then
, then
1) ![]() for any elements
for any elements ![]() and
and ![]() of the set
of the set ![]() that satisfy the condition
that satisfy the condition![]() ;
;
2)![]() ;
;
3) the equality ![]() is fulfilled for the finite set X.
is fulfilled for the finite set X.
b) if![]() , then
, then
1) ![]() for any elements
for any elements ![]() and
and ![]() of the set
of the set ![]() that satisfy the condition
that satisfy the condition![]() ;
;
2)![]() ;
;
3) the equality ![]() is fulfilled for the finite set X (see [1] [2] Theorem 6.2.3).
is fulfilled for the finite set X (see [1] [2] Theorem 6.2.3).
2. Results
Lemma 2.1. Let ![]() and
and![]() . Then the following sets are all XI-subsemilattices of the given semilattice D:
. Then the following sets are all XI-subsemilattices of the given semilattice D:
1) ![]() (see diagram 1 of the Figure 1);
(see diagram 1 of the Figure 1);
2) ![]() (see diagram 2 of the Figure 1);
(see diagram 2 of the Figure 1);
3) ![]() (see di-
(see di-
agram 3 of the Figure 1);
4) ![]() (see diagram
(see diagram
4 of the Figure 1);
5) ![]() (see diagram
(see diagram
5 of the Figure 1);
6) ![]() (see diagram 6 of the Figure 1);
(see diagram 6 of the Figure 1);
7) ![]() (see diagram 7 of the Figure 1);
(see diagram 7 of the Figure 1);
8) ![]() (see diagram 8 of the Figure 1);
(see diagram 8 of the Figure 1);
9) ![]() (see diagram 9 of the Figure 1);
(see diagram 9 of the Figure 1);
10) ![]() (see diagram 10 of the Figure 1);
(see diagram 10 of the Figure 1);
11) ![]() (see diagram 11 of the Figure 1);
(see diagram 11 of the Figure 1);
12) ![]() (see diagram 12 of the Figure 1);
(see diagram 12 of the Figure 1);
13) ![]() (see diagram 13 of the Figure 1);
(see diagram 13 of the Figure 1);
14) ![]() (see diagram 14 of the Figure 1);
(see diagram 14 of the Figure 1);
15) ![]() (see diagram 15 of the Figure 1);
(see diagram 15 of the Figure 1);
16) ![]() (see diagram 16 of the Figure 1);
(see diagram 16 of the Figure 1);
Proof: This lemma immediately follows from the ( [3] , lemma 2.4).
Lemma is proved.
We denote the following semitattices ![]() as follows:
as follows:
1)![]() , where
, where![]() ;
;
2) ![]() where
where![]() ;
;
3) ![]() where
where![]() ;
;
4) ![]() where
where![]() ;
;
5) ![]() where
where![]() ;
;
6) ![]() where
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
7) ![]() where,
where, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
8) ![]() where
where![]() ;
;
9) ![]()
10) ![]() where
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
11) ![]() where
where![]() ;
;
12) ![]() where,
where, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,![]() ;
;
13) ![]()
14) ![]()
15) ![]()
16) ![]()
Theorem 2.1. Let![]() ,
, ![]() and
and![]() . Binary relation
. Binary relation ![]() is an idempotent relation of the semigroup
is an idempotent relation of the semigroup ![]() iff binary relation
iff binary relation ![]() satisfies only one conditions of the following conditions:
satisfies only one conditions of the following conditions:
1)![]() ;
;
2)![]() , where
, where![]() ,
, ![]() , and satisfies the conditions:
, and satisfies the conditions:![]() ,
,![]() ;
;
3)![]() , where
, where![]() ,
, ![]() , and satisfies the conditions:
, and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
4)![]() , where
, where![]() ,
, ![]() , and satisfies the conditions:
, and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]()
Figure 1. All Diagrams XI-subsemilattices of the semilattice D.
5)![]() , where
, where![]() ,
,
![]() , and satisfies the conditions:
, and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
6)![]() , where
, where![]() ,
, ![]() ,
,
![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
7)![]() , where,
, where, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions: ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
8)![]() , where
, where![]() ,
,
![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
9)![]() , where
, where![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
10)![]() , where,
, where, ![]() ,
,
![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,![]() ;
;
11)![]() , where
, where![]() ,
,
![]() and satisfies the conditions:,
and satisfies the conditions:, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
12)![]() ,
,
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() and satisfies the conditions:,
and satisfies the conditions:, ![]() ,
, ![]()
![]() ,
,
![]() ,
, ![]() ,
,![]() ;
;
13)![]() , where
, where![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
14)![]() , where,
, where, ![]() ,
,
![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
15)![]() , where
, where
![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() ;
;
16)![]() ,
,
where, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
Proof. This Theorem immediately follows from the ( [3] , Theorem 2.1]).
Theorem is proved.
Lemma 2.2. If X be a finite set, then the following equalities are true:
a)![]() ;
;
b)![]() ;
;
c)![]() ;
;
d)![]() ;
;
e)![]() ;
;
f)![]() ;
;
g)![]() ;
;
h) ![]()
i) ![]()
j)![]() ;
;
k)![]() ;
;
l)![]() ;
;
m) ![]()
n) ![]()
o)![]() ;
;
p)![]() .
.
Proof. This lemma immediately follows from the ( [3] , lemma 2.6).
Lemma is proved.
Lemma 2.3. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula![]() .
.
Proof. By definition of the given semilattice D we have
![]() .
.
If the following equalities are hold
![]() ,
,
then
![]() .
.
[See Theorem 1.1] Of this equality we have:![]() .
.
[See statement a) of the Lemma 2.2.]
Lemma 2.4. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
if
![]() .
.
Then
![]() .
.
[See Theorem 1.1] Of this equality we have:
![]()
[See statement b) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.5. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
Then
![]()
[See Theorem 1.1]. Of this equality we have:
![]()
[See statement c) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.6. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
Then
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement d) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.7. Let ![]() and
and![]() .If X is a finite set, then the number
.If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
Then
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement e) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.8. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement f) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.9. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement g) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.10. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement h) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.11. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have![]() .
.
If the following equality is hold ![]() then
then![]() .
.
[See Theorem 1.1] Of this equality we have:
![]()
[See statement i) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.12. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice ![]() we have
we have
![]()
If
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement j) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.13. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
If
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement k) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.14. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have
![]()
![]()
![]()
[See Theorem 1.1] Of this equality we have:
![]()
[See statement l) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.15. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have![]() . If the following
. If the following
equality is hold ![]() then
then![]() .
.
[See Theorem 1.1] Of this equality we have:
![]()
[See statement m) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.16. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have![]() . If the following
. If the following
equality is hold ![]() then
then![]() .
.
[See Theorem 1.1] Of this equality we have:
![]()
[See statement n) of the Lemma 2.2).]
Lemma is proved.
Lemma 2.17. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. By definition of the given semilattice D we have![]() . If the following
. If the following
equality is hold ![]() then
then![]() .
.
[See Theorem 1.1] Of this equality we have:
![]()
[See statement o) of the Lemma 2.2).]
Lemma is proved.
Lemma 2.18. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]() .
.
Proof. By definition of the given semilattice D we have![]() . If the fol-
. If the fol-
lowing equality is hold ![]() then
then![]() .
.
[See Theorem 1.1] Of this equality we have:
![]() .
.
[See statement p) of the Lemma 2.2).]
Lemma is proved.
Theorem 2.2. Let ![]() and
and![]() . If X is a finite set, then the number
. If X is a finite set, then the number ![]() may be calculated by the formula
may be calculated by the formula
![]()
Proof. This Theorem immediately follows from the Theorem 2.1.
Theorem is proved.
Example 2.1. Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()