On the Foundations of Guidelines for Health Economic Assessment ()


1. Introduction
In the course of the last decades, the use of cost-effectiveness analysis as an aid to decision making in healthcare has been increasing steadily, so as to become a standard feature of medical research and medical decision making. Parallel to this, there has been a discussion of methods and foundations (see e.g. Johannesson and Weinstein [3], Dolan and Edlin [4], Meltzer and Smith [5]), although to a much smaller extent. Among the issues, which have been debated is the possibility of drawing up official guidelines for carrying out a cost-effectiveness analysis. Such guidelines have indeed been established and put to use, and in these one may observe a trend towards specification in greater detail of what must be done in order that the resulting cost-effectiveness analysis can be considered as satisfactory. This may perhaps be seen partly as a response to a demand from the pharmaceutical industry wanting exact instructions as to which documentation should be presented, partly by authorities looking for a precise set of rules regarding the information to be demanded from producers applying for market permit or drug reimbursement.
In many cases, the scientific community has been invited to participate in drawing up guidelines, so that the cost-effectiveness analyses which are made in accordance with the guidelines are those that are “best” from a purely theoretical point of view. The question of whether such scientifically correct guidelines can at all be found seems not to have attracted much, if any, attention. However, a similar question has been asked long ago in another field, which however is related, namely that of finding the “correct” accounting standards, rules for how the accounts of a company should be drawn up and presented. As pointed out by Demski [6], such correct accounting standards simply do not exist.
2. Cost-Effectiveness Analysis as an Information Service
We consider a situation where a decision maker―which in our application may be a health care organization deciding upon the best way of treating the patients under their responsibility―has to make a decision which is subject to some uncertainty. This uncertainty will be modeled in a very simple way, since we assume that there is a finite set of uncertain states, 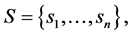 each of which affect the results of the treatment. The choices of the decision maker is given by a set A of decisions; for our purposes, a decision is a function
each of which affect the results of the treatment. The choices of the decision maker is given by a set A of decisions; for our purposes, a decision is a function 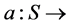 X, taking each uncertain state
X, taking each uncertain state 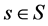 to an outcome
to an outcome 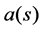 in a space of possible outcomes (to be specified later). In our application to health care, a decision is a particular treatment of patients (which may be a procedure in hospital or the administration of a particular medical drug); the effects of such treatments are usually not fully known, and neither are their costs. In our present case, we have assumed that there are some identifiable but random factors which are behind this uncertainty, which is indeed a simplification as compared with reality where the uncertainty about future consequences of a treatment tend to have a more complex nature. However, this simple structure allows us to obtain some results, which hopefully give insight into the more complicated reality.
in a space of possible outcomes (to be specified later). In our application to health care, a decision is a particular treatment of patients (which may be a procedure in hospital or the administration of a particular medical drug); the effects of such treatments are usually not fully known, and neither are their costs. In our present case, we have assumed that there are some identifiable but random factors which are behind this uncertainty, which is indeed a simplification as compared with reality where the uncertainty about future consequences of a treatment tend to have a more complex nature. However, this simple structure allows us to obtain some results, which hopefully give insight into the more complicated reality.
We shall assume that the decision maker has initial beliefs about the likelihood of each of the underlying states 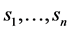 influencing outcome of the decisions, formulated as a (“prior”) probability distribution
influencing outcome of the decisions, formulated as a (“prior”) probability distribution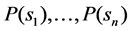 . Also, the decision cares about the consequences obtained, meaning that she has a utility function
. Also, the decision cares about the consequences obtained, meaning that she has a utility function 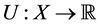 assigning utility or degree of satisfaction to each possible outcome. Relying only on the initial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utilityinitial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utility
assigning utility or degree of satisfaction to each possible outcome. Relying only on the initial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utilityinitial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utility

over all decisions . This behavior may not correspond fully to what decision makers in healthcare organizations actually do, but it is at least in line which what they pretend to do.
. This behavior may not correspond fully to what decision makers in healthcare organizations actually do, but it is at least in line which what they pretend to do.
In our discussion so far, there has been no mentioning of information; decisions were based on assessments of probabilities but not on any observation; to allow for this―and thereby formally introducing “evidence-based medicine” into the model, we should add the option of collecting and processing of information before the decision is made, which is what cost-effectiveness analysis is about. In particular, following the recent guidelines of NICE [1], information about the medical effects of a treatment should be gathered, if possible by a randomized clinical trial, which should also contain observations about health-related quality of life, and the information should be collected and processed according the specified rules. What the guidelines specify, is an information method, that is a procedure for collecting date and producing a signal (in our case, a report of the cost-effec- tiveness analysis, containing relevant cost-effectiveness ratios as well as other ingredients (such as sensitivity analysis, confidence limits etc.)
In our simplified formal world, an information method is a pair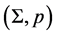 , where
, where  is a finite
is a finite
set if signals, and  is a system of conditional probabilities
is a system of conditional probabilities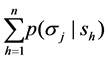 , for
, for , inter-
, inter-
preted as the probability that signal 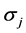 is reported given that the true state of nature is
is reported given that the true state of nature is![]() . Thus, in our model the information obtained reveals the true state of nature only partially, since there is a random error to be taken into account. This approach is in line with the usual approach to the treatment of uncertainly in cost-effective- ness analysis, cf. e.g. Drummond and McGuire [10], Drummond et al. [11], Muenig [12].
. Thus, in our model the information obtained reveals the true state of nature only partially, since there is a random error to be taken into account. This approach is in line with the usual approach to the treatment of uncertainly in cost-effective- ness analysis, cf. e.g. Drummond and McGuire [10], Drummond et al. [11], Muenig [12].
Given any observed signal![]() , the decision maker may compute posterior probabilities
, the decision maker may compute posterior probabilities ![]() of the states of nature using Bayes’ formula,
of the states of nature using Bayes’ formula,
![]()
where ![]() is the probability of observing the signal
is the probability of observing the signal![]() . Having now the updated pro-
. Having now the updated pro-
babilities over states of nature, conditional on the observed signal![]() , the choice of the decision maker must be the decision which maximizes
, the choice of the decision maker must be the decision which maximizes
![]()
over all![]() . This optimal decision, given the signal
. This optimal decision, given the signal![]() , is denoted
, is denoted![]() . The overall expected value (of taking optimal decisions, contingent on the observed signals) of the optimal decision, denoted
. The overall expected value (of taking optimal decisions, contingent on the observed signals) of the optimal decision, denoted![]() , will depend on the signal observed; before actually carrying out the observation, we may evaluate the potential gains in expected utility as
, will depend on the signal observed; before actually carrying out the observation, we may evaluate the potential gains in expected utility as
![]()
that is the difference between the ex ante expected utility with and without the information method. We call ![]() the value of the information method (at the utility function U).
the value of the information method (at the utility function U).
The value of information, as derived above, depended on the utility function U of the decision maker. Consequently, the choice of information method, if indeed such a choice is open to the decision maker, will in its turn depend on the utility function. In the case we have in mind, where an information method is a particular way of collecting and presenting data on different medical interventions, this means that the method for performing these operations should be chosen in accordance with the desires and goals of the decision maker. Simple and acceptable as this sounds, it carries a controversial message, namely that it is in general impossible to prescribe a single such method, independent of the decision maker who is going to use the results. In other word, ranking different methods of performing cost-effectiveness analysis seems not in general possible without recourse to a concrete decision maker, so that guidelines, which are applicable to all users cannot be constructed in a scientific way. In the following we give the precise formulation of this result.
For this, we need the notion that one information method is more informative that another. Let ![]() be information methods, with
be information methods, with![]() ,
,![]() . Then
. Then ![]() is more informative than
is more informative than ![]() if for each
if for each
signal ![]() such that
such that![]() , there are nonnegative numbers
, there are nonnegative numbers ![]() with
with ![]() such that
such that
![]()
An equivalent formulation of this condition is that there is an ![]() matrix R with all column sums 1 such that
matrix R with all column sums 1 such that
![]()
where ![]() is the
is the ![]() -matrix with characteristic element
-matrix with characteristic element![]() , P the
, P the ![]() matrix with characteristic element
matrix with characteristic element![]() , and R is
, and R is ![]() with elements
with elements![]() ,
, ![]() The following is a refor- mulation of a classical result of Blackwell (1948) adapted to our situation. We work with classes of acceptable utility functions which are more restricted than what is usually seen in the formulations of Blackwell’s theorem, where it is usual to allow all possible utility functions. The proof given below follows Bielinska-Kwapisz [13].
The following is a refor- mulation of a classical result of Blackwell (1948) adapted to our situation. We work with classes of acceptable utility functions which are more restricted than what is usually seen in the formulations of Blackwell’s theorem, where it is usual to allow all possible utility functions. The proof given below follows Bielinska-Kwapisz [13].
Theorem 1. Let ![]() be information methods, let
be information methods, let ![]() be a set of utility functions, A a set of actions such that for all vectors
be a set of utility functions, A a set of actions such that for all vectors![]() there are
there are ![]() such that
such that![]() ,
, ![]() ,
,![]() . Then the following are equivalent:
. Then the following are equivalent:
(i) ![]() is more informative than
is more informative than![]() ,
,
(ii) ![]() for all
for all![]() .
.
Proof: (ii)![]() (i): Suppose on the contrary that
(i): Suppose on the contrary that ![]() for all
for all ![]() but that
but that ![]() is not more informative than
is not more informative than![]() ; then by definition we have that there is a signal of the information method
; then by definition we have that there is a signal of the information method ![]() with
with ![]() such that
such that
![]()
By separation of convex sets, there must then be![]() ,
, ![]() , such that
, such that
![]()
![]()
Now we use the assumption on ![]() and A to find
and A to find ![]() and
and ![]() such that
such that ![]() ; in the following we assume that A contains only these two acts. Then for each
; in the following we assume that A contains only these two acts. Then for each ![]() we have that
we have that
![]()
since ![]() for each
for each![]() . It follows that
. It follows that
![]()
Assessing the value of the information method ![]() similarly, we get
similarly, we get
![]()
![]()
![]()
It follows that![]() , a contradiction, showing that (i) must hold.
, a contradiction, showing that (i) must hold.
(i)![]() (ii): We have that for each signal
(ii): We have that for each signal ![]() such that
such that![]() , there are nonnegative numbers
, there are nonnegative numbers ![]() with
with ![]() such that
such that
![]()
Therefore, if ![]() is the optimal decision given
is the optimal decision given![]() , then
, then
![]()
![]()
![]()
where we have used that ![]() maximizes
maximizes![]() . Multiplying by
. Multiplying by
![]()
and summing over![]() , we get that
, we get that
![]()
![]()
![]()
![]()
and it follows that![]() . ☐
. ☐
3. Conditions for Meaningfulness of Guidelines
For this, we take a closer look on the conditions on ![]() and A stated in the theorem, which state that there is a rather large supply (in terms of utility levels achieved in the different states of nature) of decisions which are in principle available. We now consider a case where this richness of action possibilities is a consequence of the underlying structure.
and A stated in the theorem, which state that there is a rather large supply (in terms of utility levels achieved in the different states of nature) of decisions which are in principle available. We now consider a case where this richness of action possibilities is a consequence of the underlying structure.
For this, we consider the environment in which a cost-effectiveness analysis is carried out. We outline briefly its theoretical background (or rather, one possible theoretical background, as there may be several, cf. Brouwer and Koopmanschap [14]): We consider medical interventions (in a broad sense) in a society with M individuals, each characterized by a vector ![]() describing current consumption of commodities and current state of health; the consumption part of the vector in its turn is a vector describing consumption of each of the l goods available,
describing current consumption of commodities and current state of health; the consumption part of the vector in its turn is a vector describing consumption of each of the l goods available, ![]() , and similarly the health component has the form
, and similarly the health component has the form![]() , where
, where ![]() measures the kth characteristic of health (which may be ability to move around, or ability to hear, or some other aspect of health). An intervention is described by the change
measures the kth characteristic of health (which may be ability to move around, or ability to hear, or some other aspect of health). An intervention is described by the change ![]() which it causes in the state (of consumption and health) of the individual i for
which it causes in the state (of consumption and health) of the individual i for![]() .
.
In the standard approach (Hansen, Hougaard, Keiding, Østerdal, [15]) it is assumed that each individual i has a utility function defined on the consumption-health pairs![]() , and the decision maker or society assesses allocations
, and the decision maker or society assesses allocations ![]() in accordance with a social welfare function S defined on m-tuples of utility levels, so that allocations are judged by the achieved value
in accordance with a social welfare function S defined on m-tuples of utility levels, so that allocations are judged by the achieved value
![]()
an approach often termed as “welfarist”. In our present setup, we do not insist that allocations are ranked exactly in this way, but only that the decisions in society are made in accordance with a utility function of the type![]() . Since an intervention is described as a change (from status-quo) in interventions, it follows that we may think of the decision maker’s utility function as defined directly on the outcomes of the interventions, that is the changes of allocation, namely by
. Since an intervention is described as a change (from status-quo) in interventions, it follows that we may think of the decision maker’s utility function as defined directly on the outcomes of the interventions, that is the changes of allocation, namely by
![]()
![]()
To make this setup fit with our model of the previous section, we assume that the changes in allocation are subject to random displacements, so that ![]() depend on the state of nature
depend on the state of nature![]() ,
, ![]() , so that an intervention takes the form
, so that an intervention takes the form![]() . In our application, the uncertainty mainly pertains to the effects of the medical treatment; the use of material resources may of course also be subject to randomness, although to a smaller extent. What does distinguish the two commodity and health components is however the possibility of compensation payments (between individuals and from outside); in the statement of our main result below we assume that effects, positive or negative, on the health components of the individuals, may be offset by suitable money compensations.
. In our application, the uncertainty mainly pertains to the effects of the medical treatment; the use of material resources may of course also be subject to randomness, although to a smaller extent. What does distinguish the two commodity and health components is however the possibility of compensation payments (between individuals and from outside); in the statement of our main result below we assume that effects, positive or negative, on the health components of the individuals, may be offset by suitable money compensations.
Theorem 2. Let A be a set of interventions of the form ![]() depending on an uncertain state of nature, which contains also the zero intervention (“do nothing”), and let be a set of utility functions of the decision maker. Assume that
depending on an uncertain state of nature, which contains also the zero intervention (“do nothing”), and let be a set of utility functions of the decision maker. Assume that
(i) A allows for all possible money compensations of health effects: For each intervention![]() , state
, state![]() , and each commodity allocation
, and each commodity allocation![]() , the set A contains an intervention
, the set A contains an intervention ![]() such that
such that
![]()
(ii) for each![]() ,
, ![]() is monotonic in the commodity components and the marginal rate of substitution between commodity and health (of any individual) is bounded (from above and below).
is monotonic in the commodity components and the marginal rate of substitution between commodity and health (of any individual) is bounded (from above and below).
If the cost-effectiveness methodology ![]() is better than
is better than ![]() for all
for all![]() , then
, then ![]() is a more detailed version of
is a more detailed version of ![]() (in the sense of being more informative).
(in the sense of being more informative).
Proof: The theorem is basically a reformulation of Theorem 1 and all that is needed is to show that A contains interventions such that for each vector![]() , there is an intervention
, there is an intervention ![]() with
with
![]()
But this follows easily from the assumptions (i) and (ii), which together show that there is an intervention, constructed from the original one combined with suitable commodity displacements in each state, such that the final utility level in each state corresponds to the vector![]() . The result now follows immediately. ☐
. The result now follows immediately. ☐
It may be noticed that our assumptions in Theorem 2 are stronger than what is really needed; indeed, we need not compensate everybody, what matters is only that some compensations can be made which make up for any loss and gain that the decision maker would experience from the uncompensated intervention. Also, it suffices to consider very small displacements since what mattered in Theorem 1 was not the absolute values of the utilities in each state but only their relative values.
4. Discussion
The implications for practice of the results are that guidelines for cost-effectiveness are of dubious value., at least when considered as a source of information. Given that the assumptions of Theorem 2 are reasonably weak and seem satisfied in practical situations where cost-effectiveness analysis is performed, the conclusion is that there can be no “best” way of setting up such an analysis. The reference case approach, specifying that observations on medical and other outcomes of an intervention should be carried out according to a standardized scheme, may have administrative merits but it has no scientific basis. The only rule that can be stated is that more detailed observation is better than less detailed information, which indeed is trivial.
Why, then, are guidelines so widespread and estimated? Again, Theorem 2 points to an answer: For purely medical interventions, the setup differs considerably from that of cost-effectiveness analysis, since there is no economic component, and obviously monetary transfers are irrelevant for the medical outcome. In such cases, information methods may indeed by ranked to an extent which permits a choice of a best one, singled out as a reference case.
What makes perfect sense in one context may however not necessarily work in another. Guidelines may be useful in medical practice and misleading in economic practice. The arguments of the present paper should indicate why this may be the case.