The Matching Equivalence Graphs with the Maximum Matching Root Less than or Equal to 2 ()
Received 23 March 2016; accepted 24 May 2016; published 27 May 2016

1. Introduction
Let G be a finite simple graph with vertex set 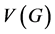 and edge set
and edge set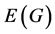 . A spanning subgraph H is called a matching of G, if every connected component of H is isolated edge or isolated vertex. k-matching of G is a matching with k edges. A matching polynomial of G is defined as
. A spanning subgraph H is called a matching of G, if every connected component of H is isolated edge or isolated vertex. k-matching of G is a matching with k edges. A matching polynomial of G is defined as
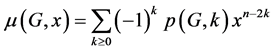
where 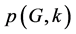 is the number of k-matchings of G.
is the number of k-matchings of G.
Two graphs G and H are called matching-equivalent if , and denoted by
, and denoted by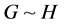 . A graph G is called matching unique if
. A graph G is called matching unique if 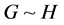 implies that
implies that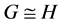 . The union of two graphs G and H, denoted by
. The union of two graphs G and H, denoted by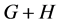 , is the graph with vertex set
, is the graph with vertex set 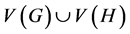 and edge set
and edge set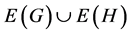 .
. 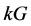 denotes the union of k graphs G.
denotes the union of k graphs G.
More than 30 years ago E. J. Farrell in [1] introduced the concept of matching polynomials. Latterly, Godsil and Gutman in [2] gave another definition. Here we use the definition given by Godsil. Form then on, the research on the properties of matching polynomials has largely been done (see [3] - [13] ). But the research on matching-equivalent of graphs is few. In this paper, we give a necessary and sufficient condition of matching equivalence of two graphs with the maximum matching root less than or equal to 2.
Throughout the paper, by 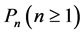 and
and , respectively, denote the path and the cycle with n vertices.
, respectively, denote the path and the cycle with n vertices. 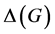 denotes the maximum degree of graph G. By
denotes the maximum degree of graph G. By ![]() denote the star graph with 5 vertices. By
denote the star graph with 5 vertices. By ![]() denote the tree which has one 3-degree vertex u and three 1-degree vertices
denote the tree which has one 3-degree vertex u and three 1-degree vertices ![]() and the distance between u and
and the distance between u and ![]() are
are![]() , respectively. A graph
, respectively. A graph ![]() is defined as the graph obtained by identifying one end of the path
is defined as the graph obtained by identifying one end of the path ![]() with a vertex of the cycle
with a vertex of the cycle![]() . Let
. Let ![]() be a path with vertices; sequence
be a path with vertices; sequence![]() ,
, ![]() denotes the tree obtained by adding pendant edges at vertices 2 and
denotes the tree obtained by adding pendant edges at vertices 2 and ![]() of
of![]() , respectively. The graphs
, respectively. The graphs ![]() are shown in Figure 1.
are shown in Figure 1.
2. Graphs with the Maximum Matching Root Less than or Equal to 2
Let G be a graph with order n. Since the roots of ![]() are real numbers (see [7] ), the maximum root of
are real numbers (see [7] ), the maximum root of ![]() denoted by
denoted by![]() , the characteristic polynomial of graph G denoted by
, the characteristic polynomial of graph G denoted by ![]() and the maximum root of
and the maximum root of ![]() denoted by
denoted by ![]() (
(![]() is also called spectral radius of graph G), respectively. In this section, we determine graphs with the maximum matching root less than or equal to 2, we firstly give some useful lemmas as follows:
is also called spectral radius of graph G), respectively. In this section, we determine graphs with the maximum matching root less than or equal to 2, we firstly give some useful lemmas as follows:
Lemma 2.1. [7] Let G be a graph with k components![]() . Then
. Then
![]()
Lemma 2.2. [7] Let G be a forest. Then![]() .
.
Lemma 2.3. [7] Let G be a connected graph and![]() . Then
. Then
1) ![]() is a single root of
is a single root of ![]() and
and![]() .
.
2) ![]() is a single root of
is a single root of ![]() and
and![]() .
.
Definition 2.1. Let G be a connected graph with a vertex u. The path-tree ![]() is a tree with the paths in G which start at u as its vertices, and where two such paths are joined by an edge if one is a maximal subpath of the other.
is a tree with the paths in G which start at u as its vertices, and where two such paths are joined by an edge if one is a maximal subpath of the other.
Clearly, if G is a tree, then the path tree![]() .
.
Lemma 2.4. [7] Let u be a vertex in the graph G and ![]() be the path tree of G with respect to u. Then
be the path tree of G with respect to u. Then
![]()
and ![]() divides
divides ![]()
Lemma 2.5. Let G is a connected graph and![]() . Then
. Then ![]() is spectral radius of path-tree
is spectral radius of path-tree![]() . i.e.,
. i.e., ![]()
Proof. By Lemmas 2.2 and 2.4, we have![]() , by Lemma 2.3, we have
, by Lemma 2.3, we have ![]() and
and![]() , comparing with the maximum root of
, comparing with the maximum root of ![]() and
and![]() , we can obtain
, we can obtain ![]()
□Lemma 2.6. [14] Let T be a tree. Then
1) ![]() if and only if
if and only if![]() ,
,
2) ![]() if and only if
if and only if![]() .
.
Theorem 2.1. Let G be a connected graph. Then
1) ![]() if and only if
if and only if![]() .
.
2) ![]() if and only if
if and only if![]() .
.
Proof. (1) Since the path-tree of ![]() respect to an arbitrary vertex and
respect to an arbitrary vertex and ![]() respect to the 3 degree vertex are
respect to the 3 degree vertex are ![]() and
and![]() , respectively. By Lemmas 2.5 and 2.6 the sufficiency is obvious.
, respectively. By Lemmas 2.5 and 2.6 the sufficiency is obvious.
Necessity:
Case 1. If G is a tree.
Clearly,![]() . By Lemma 2.6,
. By Lemma 2.6,![]() .
.
Case 2. If G isn’t a tree.
By Lemma 2.5 and 2.6, the path-tree respect to an arbitrary vertex u of G is![]() . Then we get that the maximum degree
. Then we get that the maximum degree ![]() and the number of 3-degree vertex of G is at most 1 (otherwise,
and the number of 3-degree vertex of G is at most 1 (otherwise,![]() ).
).
Subcase 2.1. If![]() . It is clear that G has only one 3 degree vertex, thus
. It is clear that G has only one 3 degree vertex, thus ![]() (otherwise,
(otherwise, ![]() or G is a tree). Clearly, the path-tree of G respect to the 3 degree vertex u is
or G is a tree). Clearly, the path-tree of G respect to the 3 degree vertex u is ![]() , Since
, Since![]() , thus we have
, thus we have![]() , i.e.,
, i.e.,![]() .
.
Subcase 2.2. If![]() .
.
Since G is connected and isn't a tree, then G is![]() . Thus
. Thus![]() .
.
(2) Since the path-tree of ![]() and
and ![]() respect to the 3 degree vertex are
respect to the 3 degree vertex are ![]() and
and![]() , respectively. By Lemmas 2.5 and 2.6 the sufficiency is clear.
, respectively. By Lemmas 2.5 and 2.6 the sufficiency is clear.
Necessity:
Case 1. If G is a tree.
Clearly,![]() . By Lemma 2.6,
. By Lemma 2.6,![]() .
.
Case 2. If G isn’t a tree.
By Lemma 2.5, the path-tree respect to an arbitrary vertex u of G is![]() , thus
, thus![]() . Denote
. Denote![]() . In order to complete the proof, we will divide four subcases as follows:
. In order to complete the proof, we will divide four subcases as follows:
Subcase 2.1. If![]() .
.
Let u is a 4 degree vertex of G. Since![]() , then
, then![]() , and thus
, and thus![]() .
.
Subcase 2.2. If ![]() and
and![]() .
.
It is clear that the number of 3 degree vertex of path-tree ![]() respect to an arbitrary vertex u of G is also greater than 2. Hence
respect to an arbitrary vertex u of G is also greater than 2. Hence![]() .
.
Subcase 2.3. If ![]() and
and![]() , then G is one of the graphs
, then G is one of the graphs ![]() and
and ![]() (see Figure 2) Clearly,
(see Figure 2) Clearly,![]() .
.
Subcase 2.4. If ![]() and
and![]() .
.
It is clear that ![]() and the path-tree respect to the 3 degree vertex u is
and the path-tree respect to the 3 degree vertex u is![]() . Since
. Since![]() , thus
, thus ![]() or
or![]() . i.e.,
. i.e., ![]() or
or![]() .
.
By Theorem 2.1 and Lemma 2.1, we can easily obtain the following Theorem 2.2:
Theorem 2.2. Let G be a graph. Then
1) ![]() if and only if every connected component of G belongs to
if and only if every connected component of G belongs to![]() .
.
2) ![]() and 2 is m multiple root of
and 2 is m multiple root of ![]() if and only if m connected components of G belong to
if and only if m connected components of G belong to ![]() and others belong to
and others belong to![]() .
.
![]()
Figure 2. Four connected graphs with ![]() and
and![]() .
.
3. Sufficient and Necessary Condition for Matching Equivalence of Graphs
In this section, the sufficient and necessary condition for matching equivalence of graphs with the maximum matching root less than or equal to 2 is determined. Firstly, we give some lemmas as follows:
Lemma 3.1. [7] Let G be a connected graph and![]() . Then
. Then
![]()
where ![]() is neighbor vertex set of u in graph G.
is neighbor vertex set of u in graph G.
Lemma 3.2. 1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12)![]() ,
,
13) ![]()
Proof. (1) Let the vertices sequence of path ![]() is
is![]() , by Lemma 3.1, consider
, by Lemma 3.1, consider ![]() with
with ![]() and
and ![]() with any one vertex, thus (1) holds.
with any one vertex, thus (1) holds.
(2) Let v be the 3 degree vertex and u be a such pendant vertex of ![]() that the distance between u and v is 1. By Lemma 3.1, consider
that the distance between u and v is 1. By Lemma 3.1, consider ![]() with u and
with u and ![]() with any one vertex, thus (2) holds.
with any one vertex, thus (2) holds.
(3)-(12) The results (3)-(12) can easily obtained by the following equalities.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(13) By Lemma 3.1, ![]() and
and
![]() . Then
. Then![]() .
.
Now, by using mathematical induction to prove (13). Firstly, By (8) and![]() ,
,
(13) holds for![]() . If
. If![]() ,
,
![]()
Hence (13) holds for![]() . □
. □
Lemma 3.3. 1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
Proof. Clearly, by Lemma 2.3, we obtain Lemma 3.3(1) immediately. And comparing with the maximum root of two sides of equalities in Lemma 3.2, other results in Lemma 3.3 is also obvious. □
Definition 3.1. Let G and ![]() be graphs, if
be graphs, if
![]()
where ![]() be integers. Then G is called a linear combination of
be integers. Then G is called a linear combination of![]() , and denote
, and denote ![]() .
.
Note that some ![]() is allowed to be negative. In fact, if all
is allowed to be negative. In fact, if all ![]() are positive, then
are positive, then ![]() is a graph. And when some
is a graph. And when some ![]() is negative for
is negative for ![]()
![]() doesn’t stand for a graph. In any case,
doesn’t stand for a graph. In any case, ![]() implies that polynomials
implies that polynomials ![]() and
and ![]() are equal. For example, since
are equal. For example, since![]() , we can denote
, we can denote![]() .
.
By Lemma 3.2, the following representations are also obvious.
Lemma 3.4. 1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
11) ![]() 12)
12)![]() .
.
Lemma 3.5. If![]() . Then G can uniquely be represented as a linear combination of the form
. Then G can uniquely be represented as a linear combination of the form
![]()
and the non-vanishing coefficient![]() , with the greatest
, with the greatest![]() , is positive. Furthermore, if
, is positive. Furthermore, if ![]() is the longest path with the non-vanishing coefficient
is the longest path with the non-vanishing coefficient![]() ,
,![]() .
.
Proof. Since![]() , by Theorem 2.2, every connected component of G belongs to
, by Theorem 2.2, every connected component of G belongs to![]() . According to Lemma 3.4, we get that G can be represented as a linear combination of paths. Next, without loss of generality, assume that G can be represented as
. According to Lemma 3.4, we get that G can be represented as a linear combination of paths. Next, without loss of generality, assume that G can be represented as
![]() (1)
(1)
where ![]() and
and![]() .
.
Now by transposition terms from side to side of Equations (1) to (2) such that the coefficients of ![]() and
and ![]() are positive, without loss of generality, Assumes that the Equation (2) as follows:
are positive, without loss of generality, Assumes that the Equation (2) as follows:
![]() (2)
(2)
where![]() ,
, ![]() and
and![]() .
.
Compare with the maximum root and its multiplicity of graphs in two sides of (2), we shall get![]() . Thus
. Thus
![]()
Repeat this proceeding, we shall get ![]() and
and ![]() for
for![]() . That is, G can uniquely be represented as a linear combination of paths.
. That is, G can uniquely be represented as a linear combination of paths.
Furthermore, assume that G be represented as a linear combination
![]() (3)
(3)
and ![]() is the non-vanishing coefficient of the longest path in (3). Then
is the non-vanishing coefficient of the longest path in (3). Then![]() .
.
In fact, assume that![]() , then by transposition terms from side to side of Equation (3) such that the coefficients of
, then by transposition terms from side to side of Equation (3) such that the coefficients of ![]() are positive, we can obtain Equation (4).
are positive, we can obtain Equation (4).
![]() (4)
(4)
where ![]() and
and![]() . By comparing with the maximum root of
. By comparing with the maximum root of ![]() and
and![]() , we can obtain
, we can obtain
![]()
![]()
it is a contradiction. Thus ![]() and then modify (4) as
and then modify (4) as
![]()
compare with the maximum root of ![]() and
and ![]() we can obtain
we can obtain
![]() □
□
Lemma 3.6. If![]() , then G can uniquely be represented as a linear combination of the form
, then G can uniquely be represented as a linear combination of the form ![]() and
and ![]() equals to the multiplicity of root 2 of
equals to the multiplicity of root 2 of![]() .
.
Proof. Since![]() , by Theorem 2.2, every connected component of G belongs to
, by Theorem 2.2, every connected component of G belongs to![]() . According to Lemma 3.4, we easily obtain that G can be represented as a linear combination of
. According to Lemma 3.4, we easily obtain that G can be represented as a linear combination of ![]() and some paths. Next, without loss of generality, assume that G can be represented as
and some paths. Next, without loss of generality, assume that G can be represented as
![]()
By transposition terms and comparing with the multiplicity of root 2, we have ![]() equal to the multiplicity of root 2 of
equal to the multiplicity of root 2 of![]() . Thus
. Thus
![]()
Furthermore, we can obtain ![]() and
and ![]() for
for![]() .
.
By Lemmas 3.5, 3.6 and Definition 3.1 we immediately get. □
Theorem 3.1. Let ![]() be graphs. Then
be graphs. Then
1) If![]() , then
, then ![]() if and only if G and H have the same linear combination repre- sentation of paths.
if and only if G and H have the same linear combination repre- sentation of paths.
2) If![]() , then
, then ![]() if and only if G and H have the same linear combination repre- sentation of
if and only if G and H have the same linear combination repre- sentation of ![]() and some paths.
and some paths.
Acknowledgements
This work is supported by National Natural Science Foundation of China (11561056), National Natural Science Foundation of Qinghai Provence (2011-Z-911), and Scientific Research Fund of Qinghai University for Nationalities (2015G02).