Understanding the Relativistic Generalization of Density Functional Theory (DFT) and Completing It in Practice ()
Received 21 January 2016; accepted 23 May 2016; published 26 May 2016

1. Introduction
From its introduction by Hohenberg and Kohn [1] , fifty one years ago, to 2014, density functional theory (DFT) and its local density approximation (LDA) [2] seemed to have serious limitations for an accurate description or the prediction of electronic and related properties of atoms, molecules, semiconductors, and insulators. Specifically, calculated energy gaps (for finite systems) and band gaps (for crystalline semiconductors and insulators) were mostly found to be unsatisfactory underestimates of the corresponding, measured values. Faced with this recalcitrant “band gap problem,” the condensed matter theory community searched for explanations of the underestimation and for remedies to it.
Self-interaction [3] and the derivative discontinuity of the exchange correlation energy [4] - [6] were respectively introduced in 1981 and 1983 to explain the perceived limitations of DFT and of its local density approximation (LDA) version. Other elements of the explanations included the fact that the exact form of the exchange correlation energy is not known; consequently, some limitations of DFT calculations could stem from approximations inherent to it and to its functional derivative, the exchange-correlation potential. In the case of LDA calculations, non-local effects are possible contributors to the disagreement between theory and experiment.
Steps taken to remedy the referenced limitations ascribed to DFT have partly consisted of the introduction of non-local versions of the exchange correlation potential, mostly in the form of generalized gradient approximations (GGA) [7] - [10] , and the construction of new potentials that have often entailed the use of fitting parameters or some other forms of adjustments or corrections. In particular, augmenting some LDA and GGA potentials with Hubbard U or other quantities is believed to improve significantly the description of strongly correlated materials [11] [12] . Hybrid versions [13] [14] of the exchange correlation potential have been particularly popular in chemistry. We should note that there appears to be a proliferation of ad hoc potentials that have the limitation of being devoid of predictive capabilities, given the fitting or adjustments that often vary from one material to another. The plethora of such potentials and the related efforts and related publications certainly take away from the search for fundamental, predictive solutions, if any. This situation is tantamount to a “band gap catastrophe”, inasmuch as accurate descriptions and predictions of properties of materials are concerned. The former and the latter are quintessentially needed for theory to inform and to guide the design and fabrications of devices and the related search for novel materials.
In 1998, our group presented exceptionally accurate, electronic and related properties of barium titanate (BaTiO3) [15] ; they were obtained with self-consistent calculations using a local density approximation (LDA) potential [16] [17] . Specifically, the calculated band gap, optical transition energies, and dielectric functions agreed very well with corresponding, experimental values for BaTiO3. Our calculated electronic and related properties for wurtzite GaN, C, and Si were also in general agreement with experiment [18] . The computational method we introduced in 1998 led to the identification of a basis set and variational effect as the source of several of the perceived limitations of DFT and LDA. The original form of this method is known as the Bagayoko, Zhao, and Williams (BZW) method [15] . After 2010, the work of Ekuma [19] and Franklin [20] resulted in an enhanced version of the method (BZW-EF). Both forms of the method are described further in Section 2. Our basis set and variational effect explanation of the underestimation of energy and band gaps by DFT calculations does not ascribe the problem to DFT, rather, it shows that calculations using a single basis set cannot search for and verifiably attain the absolute minima of the occupied energies (i.e., the ground state); for this reason, as further explained below, their results cannot be expected to have the full, physical content of DFT. Hence, disagreements with experiment cannot, for the most part, be credited to DFT.
Despite the clear success of the BZW and BZW-EF method in describing or predicting electronic and related properties of materials, as amply illustrated below, our alternative explanation of and solution to the band gap problem have mostly been ignored up to 2014. The argument has been that, without the self-interaction correction and the addition of the derivative discontinuity of the exchange correlation energy to the band gap obtained with a DFT potential, one is not expected to get an agreement with experiment. In 2014, we presented a new understanding of DFT that rigorously adheres to conditions inherent to it; i.e., we proved that these conditions have to be met by a self-consistent calculation before its results can possess the full physical content of DFT. We provide a brief review of this proof [21] below, in Section 2, and show how it completes the theory in practice. We subsequently extend this understanding to the relativistic formulation of DFT in Section 3. In Section 4, a short conclusion reiterates some salient points in this work.
2. Understanding Non-Relativistic Density Functional Theory (DFT) and Completing It in Practice
2.1. Understanding Non-Relativistic Density Functional Theory
We presented [21] a step by step recall of the derivation of density functional theory by Hohenberg and Kohn [1] . To appreciate fully what follows, the reader is urged to consult this publication [21] . For our purposes here, we summarize the key points relative to this derivation, with emphasis on their bearing on the validity of any electronic structure calculation employing a DFT potential.
The initial, non-relativistic form of density functional theory, as introduced by Hohenberg and Kohn, rests on two theorems the authors proved. The first one of these theorems states that, except for an additive constant, the external potential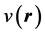 , acting on a system of electrons in a box, is a unique functional of the charge density of that system. Of course, in addition to the external potential, these electrons are subject to the electron-electron interaction. Hohenberg and Kohn [1] further established and important corollary of this theorem, namely that, with
, acting on a system of electrons in a box, is a unique functional of the charge density of that system. Of course, in addition to the external potential, these electrons are subject to the electron-electron interaction. Hohenberg and Kohn [1] further established and important corollary of this theorem, namely that, with
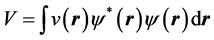 (1)
(1)
and T and U as the kinetic and electron-electron interaction operators, the energy
 , (2)
, (2)
where
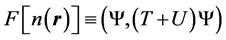 (3)
(3)
is a unique functional of the charge density.
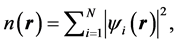 (4)
(4)
where the summation is over occupied states only.
The second theorem of Hohenberg and Kohn [1] , known as the variational principle of DFT, states that the above energy functional reaches its minimum, i.e., the ground state energy, when the density  is the ground state charge density. Specifically, provided that the admissible functions in Equation (4) are restricted by the condition
is the ground state charge density. Specifically, provided that the admissible functions in Equation (4) are restricted by the condition
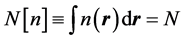 (5)
(5)
meaning that the total number of particles is kept constant.
Hohenberg and Kohn [1] established the inequality
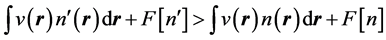 , (6)
, (6)
where 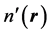 is the charge density associated with another external potential
is the charge density associated with another external potential . We emphasize the fact that, in Equation (6), the external potential
. We emphasize the fact that, in Equation (6), the external potential 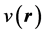 is utilized on both sides of the inequality: This inequality is the expression of the fact that the energy functional in Equation (2) attains its minimum for the correct, ground state density,
is utilized on both sides of the inequality: This inequality is the expression of the fact that the energy functional in Equation (2) attains its minimum for the correct, ground state density, 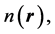 and not for a different density,
and not for a different density, 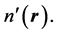 Replacing
Replacing  with
with 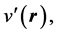 in Equation (6), reverses the direction of the inequality. Indeed, such a replacement signifies that the new system under study has a ground state charge density
in Equation (6), reverses the direction of the inequality. Indeed, such a replacement signifies that the new system under study has a ground state charge density ![]() Hence, the minimum of the energy functional can only be attained with this density.
Hence, the minimum of the energy functional can only be attained with this density.
The above steps in the derivation of density functional theory (DFT) directly lead to its rigorous, mathematical and physical understanding articulated by Bagayoko [21] , namely, for the results of electronic structure calculations to possess the full physical content of DFT, it is (a) necessary to keep the number of particles constant and (b.1) to employ the exact, three dimensional ground state charge density or (b.2) to search for and to attain the absolute minima of the occupied energies.
It is crucial to underscore here what appears to have been the key misunderstanding of DFT in many calculations, namely, the confusion between a stationary solution and the ground state solution; the former is obtained with most basis sets, following self-consistency iterations, while the latter is found after several successive, self-consistent calculations, with increasing, embedded basis sets, as explained below in connection with our computational method (BZW and BZW-EF). Embedding here signifies that, except for the first calculation with a small basis set, each of the other calculations employs the basis set of the one preceding it plus one orbital. Depending on the s, p, d, or f character of the added orbital, the size of the basis set increases by 2, 6, 10, or 14, respectively, taking the spin into account.
2.2. Completing DFT in Practice
The above new understanding of DFT requires that electronic structure calculations search for and attain the absolute minima of the occupied energies for the systems under study. Such an attainment signifies that the ground state of the system under study has been reached. As alluded to above, a self-consistent calculation with a single basis set produces a stationary solution among a potentially infinite number of such solutions. Given that such a calculation cannot claim to have attained the minimum of the energy content of the Hamiltonian in Equation (2), a unique functional of the charge density, its results should not be expected to possess the full, physical content of DFT and they generally do not, as attested to by the recalcitrance of the band gap problem. To reach the ground state energy, the use of our computational method (BZW and BZW-EF) or similar ones appears to be necessary. This method is fully described in several publications [15] [17] - [21] . We provide below a summary description of this method, with emphasis on its two features that complete DFT in practice.
The first of these features of our method is the performance of several self-consistent calculations with increasing, embedded basis sets. This implementation begins with a relatively small basis set that must be large enough to account for all the electrons in the atomic or ionic species in the molecules or solids under study. Successive, self-consistent calculations are subsequently performed, where each calculation employs the basis set of the one preceding it plus one additional orbital. Graphical and numerical comparisons of the occupied energies from two consecutive calculations, upon setting the Fermi energy to zero, show the lowering of some or of all the occupied energies as the basis set is augmented. The successive calculations stop when three consecutive ones lead to the same occupied energies, within our computational uncertainties of 0.005 eV. Three calculations are needed, given that instances were found where two consecutive calculations gave the same occupied energies, but the calculation following the second one led to some occupied energies lower than their counterparts from the two calculations. Clearly, these two calculations led to a local minimum that is not to be confused with the ground state for which absolute minima of the occupied energies are required. Further calculations, with much larger, augmented basis sets do not change the charge density. Hence, they do not change the content of the Hamiltonian, even though the corresponding matrices have larger dimensions. This feature of the BZW or BZW-EF method completes DFT in practice, inasmuch as it enables the required search and attainment of the ground state.
The above implementation of the linear combination of atomic orbitals (LCAO) is known as the Bagayoko, Zhao, and Williams (BZW) method if the added orbitals are in the order of increasing energies for the excited states in the atomic or ionic species that form the molecule or solid under study. In the BZW-EF enhancement, orbitals are not necessarily added in the order of increasing energies; rather, for a given principal quantum number n, on an atomic or ionic site, p, d, and f orbitals, if applicable, are added before the corresponding s orbital. This counter-intuitive approach recognizes the fact that, for the valence states, polarization has primacy over spherical symmetry. Even though LDA and GGA calculations with the BZW method led to accurate descriptions of several semiconductors, including predictions that have been confirmed by experiments for cubic Si3N4 [22] and InN [23] , there have been instances where band gaps obtained with the BZW method have been slightly lower than corresponding, experimental values by 0.1 to 0.3 eV. In contrast, band gaps obtained with the BZW-EF method are in agreement with experiment within the applicable uncertainties.
The second feature of the method that completes DFT in practice consists of the determination, among the potential infinite number of calculations that produce the same occupied energies, of the one that provides the DFT description of the material under study. Among the first three consecutive calculations that produce the same occupied energies, the first one, with the smallest of the three basis sets, provides the DFT description of the system. The corresponding basis set is called the optimal basis set. This choice, introduced by the BZW method and maintained in the BZW-EF enhancement, is based on the Rayleigh theorem for eigenvalues [21] [24] . This theorem states that when an eigenvalue equation is solved with basis sets with N and (N + 1) functions, where the N functions are augmented to get the (N + 1), then, the ordered eigenvalues obtained with the (N + 1) functions are lower than or equal to their corresponding ones obtained with the N functions. In other words, the increase (by augmentation) of the size of the basis set lowers a given eigenvalue, unless it has reached its minimal value; in the latter case, the eigenvalue remains unchanged.
Clearly, upon the attainment of the absolute minima of the occupied energies, a further lowering of an unoccupied energy is not due to any interaction in the Hamiltonian which does not change from its value obtained with the optimal basis set. Hence, such a lowering is a mathematical artifact stemming from the Rayleigh theorem. This artifact is the well-defined basis set and variational effect noted in the introduction. It can be invoked only after the occupied energies have reached their absolute minima; before that, the lowering of occupied and unoccupied energies is ascribed to physical interactions contained in the Hamiltonian that changes from one calculation to the next. In principle, there is an infinite number of augmented basis sets that are larger than the optimal one, some of them lower some unoccupied energies. The above referenced basis set and variational effect is not to be confused with the rather ill-defined basis set effect. In 2014, Bagayoko [20] provided a DFT based explanation for the above selection of the referenced, optimal basis set.
Indeed, the first calculation to reach the absolute minima of the occupied energies is the one providing the true DFT description of the material under study. Calculations with basis sets obtained by augmenting that of this calculation (i.e., the optimal basis set) do not change the charge density. So, as already noted, they do not change the content of the Hamiltonian. The energy content of this Hamiltonian, as given in Equation (2), is a unique functional of the charge density, according to the first Hohenberg-Kohn theorem. Another way of stating this fact is that the spectrum of the Hamiltonian is a unique functional of the charge density. Consequently, the lowered, unoccupied energies, while the charge density does not change, do not belong to the true DFT spectrum of the Hamiltonian. Such lowered, unoccupied energies, while the occupied ones do not change, explain the band gap underestimation by calculations that do not deliberately search for and attain the absolute minima of the occupied energies. The above second feature of the BZW and BZW-EF method completes DFT in practice, inasmuch as it enables the identification of the optimal basis set, i.e., that of the calculation that provides the true DFT description of the material under study. In doing so, this feature of our method avoids the destruction of the DFT or physical content of the lowest, unoccupied energies with the use of over-complete basis sets.
2.3. Experimental Confirmation of Our Understanding of DFT
Bagayoko discussed the cases of nine semiconductors [21] whose band gaps were underestimated by some 99 single basis set calculations. For each of these semiconductors, the BZW and BZW-EF results are in agreement with experiment, not just for the band gaps, but also for a host of electronic and related properties. The reader is urged to consult Reference 21 for these semiconductors that are c-InN [23] , AlAs [25] , zb-ZnS [26] , w-GaN [27] , zb-GaN [27] , rutile TiO2 [28] , w-ZnO [20] , zb-BP [29] , and c-BN [30] , where c-, w- and zb-stand for cubic, wurtzite, and zinc blende, respectively. Dozens of other semiconductors have been accurately described by DFT BZW and BZW-EF calculations, including some key, elemental ones, i.e., diamond [18] , silicon [18] , and germanium [19] .
While the above agreements attest to the correct nature of our understanding of DFT and of our completion of it in practice, the term confirmation is more appropriate for the predictions we have made and that have been later verified by experiment. Specifically, for c-Si3N4, LDA-BZW calculations of Bagayoko and Zhao [22] predicted a band gap of 3.68 eV in 2001. In 2003, Egdell et al. [31] reported two different experimental results of 3.6 eV and 3.7 eV that agree rather well with the BZW predictions. The LDA-BZW prediction for the bulk modulus of this material was 330 GPa. J. Z. Jiang et al. [32] reported a measured value of 317 ± 11 GPa, in excellent agreement with the prediction. Similarly, the LDA-BZW calculations of Bagayoko et al. [23] predicted an equilibrium lattice constant of 5.017 Å and a band gap of 0.65 eV for cubic InN (c-InN) in 2004. In 2006, Schörmann et al. [33] reported their measurements of 5.01 ± 0.01 Å for the equilibrium lattice constant and 0.61 eV for the band gap, again in agreement with the predictions.
In 2005, Bagayoko and Franklin [34] were the first to settle, with ab-initio results, the controversy between two groups of experiments about the band gap of w-InN. Before 2000, experiments mostly reported band gaps of about 2 eV. After 2000, with relatively pure crystals, experiments reported band gaps of 0.7 - 1.0 eV. The 2005 result of 0.88 eV from the LDA-BZW calculations by Bagayoko and Franklin [33] agrees rather well with the experimental one of 0.883 eV [35] , for a sample with moderate carrier concentration. Our theoretical settling of this controversy between groups of experiments is tantamount to a prediction. Wurtzite InN is well known to exhibit the Burstein-Moss effect, i.e., the increase of the band gap of a material with that of carrier concentration. Bagayoko and Franklin [34] explained how the relatively crude fabrication methods, before 2000, led to very high carrier concentrations as compared to the relatively refined, deposition methods (i.e., with molecular beam epitaxy) employed after 2000.
Our prediction of the indirect nature of the band gap of rutile TiO2 [28] , contrary to known experimental and theoretical results, deserves a special mention. Indeed, upon obtaining the indirect band gap of 2.95 eV, for rutile TiO2, and the smallest of the direct gaps of 3.05 eV, we felt compelled to publish these results. For us, it was a matter of informing the condensed matter theory community of a very rare instance where DFT-BZW-EF calculations appear to have led to an erroneous result for the band gap of a material. In 2014, Santara et al. [36] reported experimental results that show an indirect, fundamental gap for nanostructures and bulk rutile TiO2.
The above confirmation of the accuracy of LDA or GGA BZW and BZW-EF calculations for the description and prediction of electronic and related properties of materials is a motivation for extending our understanding of non-relativistic DFT to the relativistic generalization of DFT. This understanding and the accompanying completion of relativistic DFT are expected to be needed for theoretical studies of heavy elements (i.e., Z of 57 and higher) and of many systems that include them. Several high temperature superconductors, for which there remains much theoretical work to do, are examples of such materials. Depending on the degree of accuracy desired, this relativistic DFT can be very useful for the description of most atoms, molecules, semiconductors, insulators, or metals.
3. Understanding Relativistic DFT and Completing It in Practice
As we have done in the non-relativistic case, we closely follow below the derivation of the relativistic generalization of DFT, by Rajagopal and Callaway [37] , in order to elucidate its understanding that takes into account conditions that are inherent to its validity. The authors considered an arbitrary number of electrons in a box,
subject to the four-vector potential![]() . Using the formulation of quantum electrody-
. Using the formulation of quantum electrody-
namics by Schweber [38] , they wrote the Schrödinger equation in Fock space [38] as
![]() , (7)
, (7)
where the Hamiltonian is
![]() . (8)
. (8)
The terms on right hand side of the above expression follow. ![]() is the operator for describing the non-interacting Dirac and electromagnetic fields. A Fock space is an infinite dimensional vector space extensively utilized in quantum field theory to construct the states of a multi-particle system from those of a single particle system.
is the operator for describing the non-interacting Dirac and electromagnetic fields. A Fock space is an infinite dimensional vector space extensively utilized in quantum field theory to construct the states of a multi-particle system from those of a single particle system.
![]() . (9)
. (9)
![]() represents the free radiation field and
represents the free radiation field and![]() , given below, is the single particle Dirac Hamiltonian.
, given below, is the single particle Dirac Hamiltonian.
![]() . (10)
. (10)
Using the radiation gauge, the authors wrote the Coulomb interaction between electrons explicitly as
![]() . (11)
. (11)
![]() , the interaction between the transverse radiation field and matter, is
, the interaction between the transverse radiation field and matter, is
![]() . (12)
. (12)
The last term on the right hand side of Equation (8), ![]() , is the interaction between the electrons and a non-quantized external field,
, is the interaction between the electrons and a non-quantized external field,![]() . For convenience, the authors included in this external field the Coulomb field produced by the nuclei in the system. They assumed these nuclei to be fixed.
. For convenience, the authors included in this external field the Coulomb field produced by the nuclei in the system. They assumed these nuclei to be fixed.
![]() . (13)
. (13)
The above assumption of fixed nuclei consists of neglecting the motion of nuclei, as compared to that of electrons. This assumption therefore requires the classic Born-Oppenheimer approximation, i.e., that the motion of nuclei and that of electrons can be separated. Rajagopal and Callaway [37] subsequently defined the four-current density in the ground state as
![]() , (14)
, (14)
where ![]() represents the ground state of the system of matter and electromagnetic fields.
represents the ground state of the system of matter and electromagnetic fields.
The continuity equation, with the four-current density in the ground state above, is
![]() (15)
(15)
After defining the terms above, Rajagopal and Callaway proceeded to show that the external potential, ![]() , is a unique functional of the four-current density. In so doing, they established the relativistic counterpart of the first Hohenberg-Kohn theorem. As done by Hohenberg and Kohn, Rajagopal and Callaway employed le raisonnement par l’absurde (reduction ad absurdum). The usual corollary, that the energy content of the Hamiltonian is a unique functional of the four-current density, follows straightforwardly. Another way of expressing this corollary is that the spectrum of the Hamiltonian is a unique functional of the four-current density. This last formulation is particularly pertinent for electronic structure calculations employing a linear combination of four- component spinor orbitals. The above referenced energy content of the Hamiltonian is
, is a unique functional of the four-current density. In so doing, they established the relativistic counterpart of the first Hohenberg-Kohn theorem. As done by Hohenberg and Kohn, Rajagopal and Callaway employed le raisonnement par l’absurde (reduction ad absurdum). The usual corollary, that the energy content of the Hamiltonian is a unique functional of the four-current density, follows straightforwardly. Another way of expressing this corollary is that the spectrum of the Hamiltonian is a unique functional of the four-current density. This last formulation is particularly pertinent for electronic structure calculations employing a linear combination of four- component spinor orbitals. The above referenced energy content of the Hamiltonian is
![]() (16)
(16)
where
![]() . (17)
. (17)
Following the approach of Hohenberg and Kohn, Rajagopal and Callaway [37] established the relativistic counterpart of the second Hohenberg-Kohn theorem. They first integrated the continuity equation to obtain
![]() . (18)
. (18)
Equation (18) is the expression of the requirement to have the total number of particles kept constant.
With ![]() and
and ![]() as the ground state vectors corresponding to two different external potentials
as the ground state vectors corresponding to two different external potentials ![]() and
and![]() , respectively, Rajagopal and Callaway proved the following inequality,
, respectively, Rajagopal and Callaway proved the following inequality,
![]() , (19)
, (19)
with ![]() on both sides of the inequality.
on both sides of the inequality.
The above inequality, in Equation (19) above, expresses the relativistic counterpart of the second Hohenberg- Kohn theorem.
As in the case of non-relativistic DFT, the use of the relativistic generalization of DFT for electronic structure calculations has the following requirements, if the results are to possess the physical content of relativistic DFT: (a) the number of particles has to be kept constant and (b.1) one has to utilize the correct ground state current density or (b.2) one has to search for and reach the absolute minima of the occupied energies. As in the non-re- lativistic case, the four-current density corresponding to the absolute minima of the occupied energies is that of the ground state. Again, Equation (19) clearly shows that the results of calculations with a single four-component spinor basis set cannot be expected to provide the correct relativistic DFT description of a material. Such results are merely from an arbitrary, stationary solution out of a practically infinite number of such solution.
4. Conclusion
From the above understanding of the non-relativistic and relativistic density functional theory (DFT), it follows that failures of single basis set calculations to produce the correct description of materials stems from their non- adherence to one condition inherent to the validity of DFT. Indeed, in the absence of a known, exact ground state charge or four-current density, the search and attainment of the absolute minima of the occupied energies is simply required for results of electronic structure calculations to possess the full, physical content of relativistic or non-relativistic DFT. The Bagayoko, Zhao, and Williams (BZW) method, as enhanced by Ekuma and Franklin (BZW-EF) leads to highly accurate descriptions and predictions of electronic and related properties of materials, with DFT potentials. It does so without invoking the derivative discontinuity of the exchange correlation energy or self-interaction correction. Further, with this method, one does not seem to need ad hoc potentials to obtain or to approach results in agreement with experiment. The above understanding of DFT and the BZW-EF method open the way for highly accurate descriptions and predictions of electronic and related properties of materials. In so doing, they enable theory to inform and to guide the design and fabrication of material-based devices.
Acknowledgements
This work was funded in part the US National Science Foundation [NSF, Award Nos. EPS-1003897, NSF (2010- 2015)-RII-SUBR, and HRD-1002541], the US Department of Energy, National Nuclear Security Administration (NNSA, Award No. DE-NA0002630), LaSPACE, and LONI-SUBR. The author thanks Ms. Lashounda Franklin for her assistance in editing this article.