Fixed Points Associated to Power of Normal Completely Positive Maps* ()
Received 1 April 2016; accepted 21 May 2016; published 24 May 2016

1. Introduction
Completely positive maps are founded to be very important in operator algebras and quantum information. Especially recent years, it has a great development since a quantum channel can be represented by a trace preserving completely positive map. Fixed points of completely positive map are useful in theory of quantum error correction and quantum measurement theory and have been studied in several papers from different aspects, many interesting results have been obtained (see [1] - [12] ).
For the convenience of description, let H be a separable complex Hilbert space and 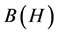 be the set of all bounded linear operators on H. Let
be the set of all bounded linear operators on H. Let ![]() on
on ![]() be a contractive
be a contractive ![]() map. As we know, every contractive and normal (or weak
map. As we know, every contractive and normal (or weak ![]() continuous) completely positive map
continuous) completely positive map ![]() on
on ![]() is determined by a row contraction on H in the sense that
is determined by a row contraction on H in the sense that
![]()
where if![]() , the convergence is in the weak * topology (see [13] and [14] ) and then denoting
, the convergence is in the weak * topology (see [13] and [14] ) and then denoting![]() , we call
, we call ![]() a completely positive map associated with A.
a completely positive map associated with A.
Let ![]() be an at most countable subset of
be an at most countable subset of ![]() with
with![]() , where the series is convergent in the strong operator topology. In this case, A is called a row contraction. Then
, where the series is convergent in the strong operator topology. In this case, A is called a row contraction. Then ![]() is well defined on
is well defined on ![]() and also a normal completely positive map. Moreover, we denote j-power for
and also a normal completely positive map. Moreover, we denote j-power for ![]() by
by![]() , that is
, that is![]() . In addition, For a row contraction
. In addition, For a row contraction![]() , we say that the operator sequence A is unital if
, we say that the operator sequence A is unital if ![]() is commutative, if
is commutative, if ![]() for all
for all ![]() is normal, if each
is normal, if each ![]() is normal and positive, and if every
is normal and positive, and if every ![]() is positive. If A is unital (resp. commutative) then we say that
is positive. If A is unital (resp. commutative) then we say that ![]() is unital (resp. commutative). Moreover,
is unital (resp. commutative). Moreover, ![]() or A is called trace preserving if
or A is called trace preserving if![]() . For a subset
. For a subset![]() , we denote the commutant of S in
, we denote the commutant of S in ![]() by
by![]() . We say that an
. We say that an ![]() is a fixed point of
is a fixed point of ![]() or a fixed point associated to the row contraction A if
or a fixed point associated to the row contraction A if![]() . Let
. Let ![]() be the set of fixed points of
be the set of fixed points of![]() . Some authors compared the commutant
. Some authors compared the commutant ![]() of
of![]() , where
, where![]() , and some conditions for which
, and some conditions for which ![]() are given (as in [1] , [10] ).
are given (as in [1] , [10] ).
For a trace preserving quantum operation![]() , it was proved that
, it was proved that ![]() if
if ![]()
in [1] . And![]() , if Kraus operators A is a spherical unitary [10] . On the other hand, the authors [12] consider some conditions for a unital and commuting row contraction A to be normal and therefore
, if Kraus operators A is a spherical unitary [10] . On the other hand, the authors [12] consider some conditions for a unital and commuting row contraction A to be normal and therefore ![]() in those cases. Moreover, the fixed points set
in those cases. Moreover, the fixed points set ![]() of
of ![]() is represented when A is a commuting and trace preserving row contraction [15] .
is represented when A is a commuting and trace preserving row contraction [15] .
The purpose of this paper is to investigate fixed points of j-power of the completely positive map ![]() for
for
![]() . It is obtained that
. It is obtained that ![]() and
and ![]() when A is self-adjoint and commutable. Furthermore,
when A is self-adjoint and commutable. Furthermore, ![]() holds under certain condition.
holds under certain condition.
2. Main Results
In this section, let A be a normal and commuting row contraction. To give main results, we begin with some notations and lemmas. Let ![]() be the strong operator topology limit of
be the strong operator topology limit of![]() .
.
Lemma 1 ( [10] ) Let ![]() be a unital and normal commuting row contractions. Then
be a unital and normal commuting row contractions. Then![]() .
.
Lemma 2 ( [10] ) Let ![]() be a commuting row contraction. If
be a commuting row contraction. If![]() , then there exists a triple
, then there exists a triple ![]() where K is a Hilbert space,
where K is a Hilbert space, ![]() is a bounded operator from K to H and
is a bounded operator from K to H and ![]() is a spherical unitary on K satisfying the following properties:
is a spherical unitary on K satisfying the following properties:
1)![]() ;
;
2) ![]() for all k;
for all k;
3) K is the smallest reducing subspace for ![]() containing
containing![]() ;
;
4) The mapping
![]()
defined by
![]()
is a complete isometry from the commutant of ![]() onto the space
onto the space![]() ;
;
5) There exists a *-homomorphism ![]() such that
such that
![]() .
.
Lemma 3 ( [16] ) (Fuglede-Putnam Theorem) Let![]() , if A and B are normal, then
, if A and B are normal, then ![]() implies
implies![]() .
.
In general, there is no concrete relation between ![]() and
and ![]() for different positive integers k and j.
for different positive integers k and j.
Example 4 Let ![]() and
and![]() , then
, then ![]() is well defined and
is well defined and ![]() . However, by a direct computation,
. However, by a direct computation, ![]() and
and![]() . Hence,
. Hence,![]() .
.
But if A is self-adjoint and commutable, the following result holds.
Theorem 5 If A is unital, self-adjoint and commutable, then ![]() and
and ![]() for any
for any![]() .
.
Proof. For any![]() , we first prove
, we first prove![]() . For any
. For any![]() , then
, then![]() . So
. So![]() for any j. It is only to prove
for any j. It is only to prove![]() . According to A is unital, self- adjoint and commutable, then
. According to A is unital, self- adjoint and commutable, then ![]() is so. For any operator
is so. For any operator![]() , then A and
, then A and ![]() are commutable for any k by lemma 1. By the function calculus, A and
are commutable for any k by lemma 1. By the function calculus, A and ![]() are commutable
are commutable
since ![]() is self-adjoint, and so
is self-adjoint, and so![]() . Therefore,
. Therefore,
![]() .
.
Next, we prove![]() . For any
. For any![]() , then
, then
![]() , for any
, for any![]() .
.
So ![]() since
since![]() , thus
, thus![]() . It follows that
. It follows that ![]()
and![]() . So
. So![]() . Conversely, for any
. Conversely, for any![]() ,
,![]() , then
, then![]() . So
. So ![]() for any j. Therefore
for any j. Therefore![]() . So
. So ![]() and
and ![]() . Therefore, the result holds. This completes the proof.
. Therefore, the result holds. This completes the proof.
Corollary 6 Let ![]() be unital, self-adjoint and commutable, then
be unital, self-adjoint and commutable, then
![]() ,
,
where ![]()
Proof. From Theorem 5 and Lemma 1, it is only to prove that![]() . Let
. Let ![]() and
and![]() , for any operator
, for any operator![]() , then
, then![]() .
.
From Lemma 1, we have
![]() .
.
It follows that ![]() for any k and then
for any k and then![]() . This completes the proof.
. This completes the proof.
Theorem 7 Let ![]() be unital and commutable. Supposing that there is an
be unital and commutable. Supposing that there is an ![]() such that
such that ![]() is positive and invertible, then
is positive and invertible, then![]() , where
, where![]() .
.
Proof. From Lemma 2, there exists a triple ![]() where K is a Hilbert space,
where K is a Hilbert space, ![]() is abounded operator and
is abounded operator and ![]() is a normal unital and commuting operator sequence on K having the properties 1)
is a normal unital and commuting operator sequence on K having the properties 1)![]() ; 2)
; 2)![]() ; 3) K is the smallest reducing subspace for
; 3) K is the smallest reducing subspace for ![]() containing
containing![]() ; 4) The mapping
; 4) The mapping ![]() defined by
defined by ![]() and
and ![]() is a complete isometry from the commutant of
is a complete isometry from the commutant of ![]() onto the space
onto the space![]() ; also it is obtained that
; also it is obtained that ![]() for any k, where
for any k, where ![]() is a unital *-homomorphism. Then
is a unital *-homomorphism. Then ![]() is positive and invertible since
is positive and invertible since ![]() is positive and invertible. Next, we write
is positive and invertible. Next, we write ![]() and
and ![]() for any
for any![]() . In fact,
. In fact, ![]() if and only if
if and only if ![]() for any
for any![]() . On one hand,
. On one hand, ![]() if
if![]() ; on the other hand, if
; on the other hand, if![]() , then
, then ![]() and so
and so ![]() by the function calculus. Moreover,
by the function calculus. Moreover, ![]() , thus
, thus ![]() since
since ![]() is invertible. That is to say,
is invertible. That is to say, ![]() and
and ![]() have the same reducing subspace. It follows that K is also the smallest reducing subspace for the unital, normal and commuting operator sequence
have the same reducing subspace. It follows that K is also the smallest reducing subspace for the unital, normal and commuting operator sequence ![]() containing
containing![]() . Thus
. Thus ![]() is also a complete isometry from the commutant of
is also a complete isometry from the commutant of ![]() onto the space
onto the space![]() . Combining with
. Combining with![]() , it is easy to get
, it is easy to get![]() . The proof is completed.
. The proof is completed.
Acknowledgements
This research was supported by the Natural Science Basic Research Plan of Henan Province (No. 14 B110010 and No. 1523000410221).
NOTES
![]()
*Fixed points of completely positive maps.