Measuring Crustal Lg-Waves Attenuation in the Northern Part of Africa ()
Received 7 March 2016; accepted 21 May 2016; published 24 May 2016

1. Introduction-Objectives
Attenuation of regional seismic waves has been studied for years from various points of view including theoretical researches and numerous applied researches in various geophysical environments. Among these studies, Lg-waves have often been studied in order to characterize continental crust, because these wavetrains are often those which carry the most part of the seismic energy. Resulting from both theoretical and observational studies, it is now widely recognized that attenuation of Lg-waves can be represented by two terms:
・ The first one only represents the conservation of energy as a function of distance from the source. Thereby, this geometrical attenuation is simply represented by a decaying function of distance: 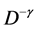 characterized by a unique value
characterized by a unique value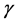 .
.
・ The second one represents all the effects of inelastic attenuation, such as energy loss or energy redistribution such as scattering. This term is represented by a function of distance and frequency, controlled a quality factor Q, which appears to also depend on frequency: 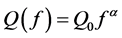 [2] [3] .
[2] [3] .
Aki (1969) [4] was the first researcher who observed that the seismic Lg-coda could be fruitful to study this quality factor, even by the use of a unique station. From this key study, numerous theoretical studies have been conducted, in particular to try to separate the two origins of inelastic attenuation. This is still a difficult problem, because the theoretical models are very similar. Nevertheless, some authors [5] - [7] have shown using simulation that the early part of the coda is mainly controlled by scattering attenuation, and the late coda is controlled by intrinsic attenuation. Also, observations of Lg-codas have been used to measure the Lg Q-factor in various crustal structures. As a general rule, in tectonic areas, Q0 can be less than 100, and strongly depends on frequency with 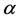 close to 1 [8] but in the opposite, in stable areas such as cratons, Q0 can be as high as one or 2000 [2] [3] and slightly depends on frequency with
close to 1 [8] but in the opposite, in stable areas such as cratons, Q0 can be as high as one or 2000 [2] [3] and slightly depends on frequency with 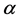 nearly equal to 0.1. Due to an evident lack of seismicity, and consequently often a lack of stations, in theses stable areas, the Q factor is not documented as well as in tectonic areas. In particular, in North Africa, most of the studies are carried out on the borders of the continent:
nearly equal to 0.1. Due to an evident lack of seismicity, and consequently often a lack of stations, in theses stable areas, the Q factor is not documented as well as in tectonic areas. In particular, in North Africa, most of the studies are carried out on the borders of the continent:
・ Using seismic networks in Spain and Morocco, [9] had established a map of the propagation efficiency of Lg and Sn waves between the north of Africa and the south of Europe;
・ [8] proposed a tomography of Lg wave attenuation from Turkey to Arabia, leading to strong variations of the quality factor, less than 100 in the western and eastern parts of Turkey, and between 600 and 800 in the Arabian plate;
・ The East African Plateau had been studied by [10] who had tried to separate intrinsic and scattering Q, leading to QI between 300 and 600, and QS between 1000 and 2000;
・ Finally, in the south-west, in the area of Mount Cameroon, [11] used a local network and the local seismicity which is detected to study attenuation close to the volcano: they found a very low attenuation: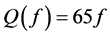 .
.
From 2007, a broadband seismic station has been installed in Chad close to the city of Abeche in the eastern part of the country, and is operated by the University of N’Djamena. Recording well developed Lg-wavetrains generated by earthquakes located in the tectonic areas surrounding the north of Africa, this station can be efficiently used to study the Lg Q-factor in this wide stable area. In the following, we successively present the used dataset, the processing method and finally discuss the results.
2. Data
The seismic station is ideally situated in the middle of the Nubian plate, which is mainly composed of different cratons and various old geological features, their story beginning during the proterozoic era. The oldest Archean cratons in Africa (West Africa, Congo and Kalahari) are separated by more weak grounds [12] which exhibit a little seismicity, such as the Sirt basin, the North of Egypt [13] and the volcanic line of mount Cameroon [14] . A little seismic activity is also found along the coast line and along the passive Atlantic margin. Not yet fully understood, this seismicity cannot be explained by the velocity inside the Nubian plate (less than 0.6 mm/year [15] : much lower than the velocities which can be observed on the edges of the Nubian plate: the convergence velocity between Nubia and Eurasia is close to 5 mm/year, and can reach up to 25 mm/year at the south of the Hellenic arc). To the east, Nubia is going away of Arabia at roughly 20 mm/year [16] and the divergence velocity through the East African Rift ranges from 6 to 3 mm/year from North to South [15] [17] .
This situation explains that the events recorded by the ABC (Abeche) seismic station are mainly located far from the station, more precisely at distances greater than 1700 km (Table 1, Figure 1). Nevertheless, due to a very low seismic noise, as shown by Figure 2, most of them have developed a well-defined Lg wave train followed by a long duration coda, as shown by the top part of Figure 3. From all these events, we have selected those for which an Lg-wavetrain can be clearly identified. These events are shown by colored dots on Figure 1, color representing magnitude. Then, it appears that some seismic areas cannot be investigated, due to the lack of Lg waves such as the events located south of Italy for which the path travels through the oceanic crust lying between Italy and Africa, which extends also a bit between Greece and Africa. Finally, some events occurred off the western coast of Africa near Morocco; these are low magnitude events, very far from our station, which does not record any available coda.
Furthermore, the special case of the event located in south Algeria, close to the city of Tamanrasset, is of major interest. This mb 4.2 event clearly occurs in a very stable area; it is well recorded in the ABC station as shown by Figure 3. Fortunately, a seismic station, operated by the GeoScope French institute, is located close to the city. The recorded data show a very nice record of this event, as shown by the bottom part of Figure 3. This record
![]()
Figure 1. Geographical distribution of the studied events (circles) and Chad station ABC (diamond) displayed on a map of Africa; black little crosses indicate the natural seismicity (magnitude greater than 4) during the studied timeframe.
![]()
Figure 2. Averaged (median) background seismic noise for ABC station (black line), compared with the Peterson’s noise model (NLNM, 1993) [18] (dotted line).
![]()
![]()
Figure 3. Records and time-frequency distribution of energy for the Tamanrasset event; top: Chad station (ABC), bottom: Tamanrasset station (TAM).
exhibits a well developed coda ranging at least 600 s, very fruitful for coda-Q measurement.
3. Processing
As described in the introduction, we have used the original model of coda decay, proposed by [4] in which the amplitude is represented by a function of frequency and time as follows:
 . In this equation, C(f) is the source term,
. In this equation, C(f) is the source term,  is the geometrical attenuation and Qc characterises the effects of inelasticity. For each frequency band centered around frequency f, the logarithm of the envelope of the filtered coda, computed by a smoothed Hilbert transform, is fitted by a straight line, the slope of which representing the Qc factor for frequency f (Figure 4).
is the geometrical attenuation and Qc characterises the effects of inelasticity. For each frequency band centered around frequency f, the logarithm of the envelope of the filtered coda, computed by a smoothed Hilbert transform, is fitted by a straight line, the slope of which representing the Qc factor for frequency f (Figure 4).
The frequency bands are organised by a logarithmic scale, covering the range [0.1; 5] Hz. However, depending on the events, the available frequency bands are limited for most of them to the [0.5; 2] Hz band.
Finally, for each event we compute the frequency dependency of Qc (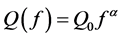 ), as shown by Figure 5, in which the retained values of Q are chosen manually before computing the linear regression.
), as shown by Figure 5, in which the retained values of Q are chosen manually before computing the linear regression.
4. Results
4.1. Estimating the Stability of the Results
In order to evaluate the stability of the processing, we have selected 6 events which occurred in the same area (south of Kenya) at a distance of roughly 3000 km from the station. These events occurred the same day (i.e. December 6, 2009), and their magnitudes range from 4.5 to 5.0. Table 1 gives the results in terms of Q0 and 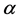 coefficients. It shows that the Q0 factor is more stable (i.e. 718 ± 7) than (i.e. 0.6 ± 0.1), which can be explained by the low range of available frequencies.
coefficients. It shows that the Q0 factor is more stable (i.e. 718 ± 7) than (i.e. 0.6 ± 0.1), which can be explained by the low range of available frequencies.
4.2. Global and Regional Results
The results for the global dataset (namely 70 events) are presented on Figure 6 by a color scale. In order to
![]()
Figure 4. For each frequency band, centered on the f0 frequency displayed at the top of each plot, the logarithm of the coda envelope is represented by a color curve and the smoothed coda by a black curve; the white line, delimited by the vertical dashed lines, is the portion of coda which is used for computing the Q value.
![]()
Figure 5. Final estimation of Qc factor: the red circles are the Qc estimated by the fit of the linear part of the coda; the black line is the best linear fit of the selected values delimited by the two vertical dashed lines. The blue dots are the Qc values which are not selected.
![]()
Table 1. Results obtained for 6 events located close to one another showing the dispersion of the results.
estimate some regional effects, we have grouped the events by region and computed average values of Q0 and![]() ; Table 2 presents these values.
; Table 2 presents these values.
Although the values are not very different from one region to others, we can see that the lowest values are obtained for events in Turkey, according to a propagation partly in the oceanic crust in the central Mediterranean Sea, and the highest ones are obtained for the events in the East African Rift, in the considerable exception of the event located close to Tamanrasset in South Algeria, discussed in the following section.
4.3. Special Case of Tamanrasset Event
As discussed earlier, this event is very particular because it occurred in the middle of the stable plate, providing a path fully included into the continental plate. Fortunately, the GeoScope French global network operates a station close to Tamanrasset, which has recorded this event. Figure 3 shows time-frequency plots of the records at both stations; they show a well-developed coda ranging to at least 400 s after the Lg arrival-time for the Chad station, and more than 500 s for the Tamanrasset station. Finally, Table 3 gives the parameters resulting from the processing. Despite the very different distances of propagation, these results show very similar values for both Q0 and a. This is a strong indication that our measures of Q0 correspond to an averaged value available for
![]()
Figure 6. Geographical representation of the Q0 factor obtained for each event (color scale).
![]()
Table 2. Averaged results for the main regions of interest and for the global dataset.
![]()
Table 3. Q0 and a parameters obtained for the Tamanrasset earthquake at Chad (ABC) and Tamanrasset (TAM) stations.
the whole stable crust of the northern part of Africa.
4.4. 3-Component Results
The Chad station in Abéché is equipped with a 3-component seismometer. In this section, we compare results obtained by the coda processing on each component.
Unfortunately, background seismic noise is often higher on horizontal components than on the vertical one.
![]()
Figure 7. Comparison between Qc computed on the vertical and east components. The black line is the best linear fit assuming crossing 0.
This leads to a less important dataset; more precisely, only 30 of the original 70 events can be used to compute the horizontal Qc factor. Figure 7 is a plot of the resulting Q0 for these events; the black line is the best linear fit assuming crossing 0; it leads to an averaged ratio very close to 1, suggesting that there is no evidence of any difference between vertical and horizontal coda generations.
4.5. Discussion-Conclusion
We have taken advantage of the ideal situation of the seismic station ABC (Abeche, Tchad) in the center of the northern part of Africa, which is a quiet seismic area and a very stable tectonic plate. Seismicity is located in the outskirts of the plate, at distances often greater than 1500 km , mainly in the north and east directions. Due to this stability, Lg-waves can propagate in the crust over long distances and are then recorded on the ABC station. Lg-codas are then used to study attenuation of Lg-waves in the crust according to Aki’s formulation. For the whole area, we have found a frequency dependence described by the following formula: ![]() similar values are obtained for the attenuation measured on horizontal components. However, some events lead to lower values indicating higher attenuation; they are located close to South Turkey, which is consistent with the fact that no Lg-waves are recorded at ABC for events located in this area. Finally, the largest value is obtained for an event located in the middle of the place close to the city of Tamanrasset. Using records of the station TAM located close to the event, we obtained a very similar value for the attenuation; this strongly validates that the obtained values represent the attenuation at the global scale.
similar values are obtained for the attenuation measured on horizontal components. However, some events lead to lower values indicating higher attenuation; they are located close to South Turkey, which is consistent with the fact that no Lg-waves are recorded at ABC for events located in this area. Finally, the largest value is obtained for an event located in the middle of the place close to the city of Tamanrasset. Using records of the station TAM located close to the event, we obtained a very similar value for the attenuation; this strongly validates that the obtained values represent the attenuation at the global scale.