Received 25 April 2016; accepted 20 May 2016; published 23 May 2016

1. Introduction
First and foremost, by starting from radical and controversial assumptions, Heisenberg himself attributed a general and far-reaching status to his own uncertainty principle. We are prepared to be confronted with Heisenberg’s most radical step.
“Weil alle Experimente den Gesetzen der Quantenmechanik und damit der Gleichung (1) unterworfen sind, so wird durch die Quantenmechanik die Ungültigkeit des Kausalgesetzes definitiv festgestellt.” [1]
Translated into English:
“Because all experiments are governed by the laws of quantum mechanics and thus far by equation (1), it is therefore that quantum mechanics has established the invalidity of the principle of causality definitively.”
We are faced with the necessity of a radical revision of the foundation for the explanation and description of objective reality as such. We shall not go too deeply into this matter but it is precisely this requirement which prevents us from being able to take into account that Heisenberg’s uncertainty principle can be treated as mathematically and logically consistent.
2. Material and Methods
Logically or mathematically, Heisenberg’s uncertainty principle is formulated as a non strict inequality.
2.1. Definitions
2.1.1. Definition: Strict Inequalities
In terms of algebra, a strict inequality possesses either the symbol > (strictly greater than) or < (strictly less than). A strict inequality is without an equality condition. In general, it is
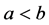 (1)
(1)
while the notation a < b means that “a is strictly less than b”. In the same respect, it is
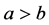 (2)
(2)
while the notation a > b means that “a is strictly greater than b”.
2.1.2. Definition: Non-Strict Inequalities
In contrast to strict inequalities, a non strict inequality is an inequality where the inequality symbol is ≥ (either greater than or equal to) or ≤ (either less than or equal to). Consequently, a non strict inequality is an inequality which has equality conditions too. In terms of algebra, we obtain
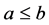 (3)
(3)
The notation a ≤ b means that “a is either less than or equal to b”. Equally it is
 . (4)
. (4)
The notation a ≥ b means that “a is either greater than or equal to b”. A non strict inequality can lead to a either or fallacy, a so called “black or white” fallacy.
2.1.3. Definition: Heisenberg’s Uncertainty Principle
A preliminary and simplistic formulation of the quantum mechanical uncertainty principle for momentum and position can be found in Heisenberg’a article of 1927, entitled as “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik” as
“Im Augenblick der Ortsbestimmung… verändert das Elektron seinen Impuls unstetig. Diese Änderung ist um so größer, je kleiner die Wellenlänge des benutzten Lichtes, d. h. je genauer die Ortsbestimmung ist… also je genauer der Ort bestimmt ist, desto ungenauer ist der Impuls bekannt und umgekehrt” [1] .
Translated into English:
“When the position is determined… the electron undergoes a discontinuous change in momentum. This change is the greater the smaller the wavelength of the light employed, i.e., the more exact the determination of the position… thus, the more precisely the position is determined, the less precisely the momentum is known, and conversely.”
Let us now move to another question about Heisenberg’s uncertainty principle. Speaking, as it is often done, Heisenberg himself did not provide a general and exact derivation of his uncertainty principle. Finally, on a more formal level, we note that the first mathematically exact formulation of Heisenberg’s uncertainty principle is due to Kennard [2] . In particular, in his Chicago Lectures Heisenberg himself pointed out that Kennard’s proof “does not differ at all in mathematical content” [3] from the argument he had presented earlier. Finally, the only difference is that Kennard’s proof “is carried through exactly” [3] . Heisenberg’s uncertainty principle often reads as
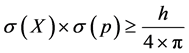 (5)
(5)
where σ(p) is the standard deviation of momentum, σ(X) is the standard deviation of position, h is Planck constant and π is the mathematical constant. Heisenberg’s explanation of the relationship between position and momentum is not defined as an equality in the sense that . Heisenberg explains the relationship between position and momentum as a non-strict inequality as
. Heisenberg explains the relationship between position and momentum as a non-strict inequality as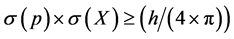 . Thus far and contrary to expectation, Heisenberg is not demanding that two different terms either
. Thus far and contrary to expectation, Heisenberg is not demanding that two different terms either  or
or 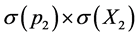 are needed to fulfill his above non-strict inequality. Heisenberg demands that the same term
are needed to fulfill his above non-strict inequality. Heisenberg demands that the same term 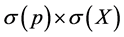 must fulfill the non-strict inequality
must fulfill the non-strict inequality . The logical form of Heisenberg’s uncertainty principle is either
. The logical form of Heisenberg’s uncertainty principle is either
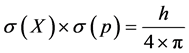 (6)
(6)
is true or
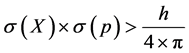 (7)
(7)
is true. From Equation (7) follows that
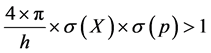 . (8)
. (8)
The following table is able to illustrate the last relationship (Table 1).
![]()
Table 1. Heisenberg’s uncertainty principleas a strict inequality.
Due to Equation (8), Heisenberg’s uncertainty principle demands that
![]() . (9)
. (9)
2.1.4. Definition: Heisenberg’s Term H
In general, we define Heisenberg’s term H as
![]() . (10)
. (10)
Under conditions of Equation (9) Heisenberg’s term H has to be greater than zero or it is
![]() . (11)
. (11)
2.2. Axioms
Axiom I. (Lex identitatis).
To avoid any kind of a logical fallacy, the following theory is based on the axiom:
![]() (12)
(12)
3. Results
3.1. Theorem: Heisenberg’s First Way to Define the Number 1
Claim.
Heisenberg’s uncertainty principle defines the number 1 as
![]() . (13)
. (13)
Direct proof.
Due to our Axiom I, it is
![]() . (14)
. (14)
We multiply the equation before by the term ![]() and do obtain the relationship
and do obtain the relationship
![]() . (15)
. (15)
According to Equation (6), this is equivalent with
![]() . (16)
. (16)
Under these conditions, Heisenberg’s term H is not needed or can be set to H = 0 to define the number +1. In general, Heisenberg’s uncertainty principle defines the number +1 under conditions of Equation (6) as
![]() . (17)
. (17)
Quod erat demonstrandum.
3.2. Theorem: Heisenberg’s Second Way to Define the Number 1
Claim.
Heisenberg’s uncertainty defines the number 1 in the same respect in a second way as
![]() . (18)
. (18)
Direct proof.
Due to our Axiom I, it is
![]() . (19)
. (19)
We add 0 to Equation (19) and do obtain the relationship
![]() . (20)
. (20)
Using the same term ![]() as before, Equation (20) can be rearranged as
as before, Equation (20) can be rearranged as
![]() (21)
(21)
and simplified in general as
![]() . (22)
. (22)
Heisenberg’s term is defined as![]() . Thus far, the number +1 is the same and does not depend under conditions. Consequently, even under conditions of Equation (7) it is possible to define the number +1. Heisenberg’s uncertainty principle defines the number +1 under conditions of Equation (7) and due to Equation (10) and Equation (11) as
. Thus far, the number +1 is the same and does not depend under conditions. Consequently, even under conditions of Equation (7) it is possible to define the number +1. Heisenberg’s uncertainty principle defines the number +1 under conditions of Equation (7) and due to Equation (10) and Equation (11) as
![]() . (23)
. (23)
Quod erat demonstrandum.
The following table may illustrate this relationship (Table 2), which is equivalent with Table 3.
![]()
Table 2. Heisenberg’s uncertainty and the number 1.
![]()
Table 3. Heisenberg’s uncertainty and the number 1.
3.3. Theorem: Refutation of Heisenberg’s Uncertainty Principle in General
Claim.
Heisenberg’s uncertainty principle is neither mathematically nor logically correct. If you accept Heisenberg’s uncertainty principle as valid then you must accept too that
![]() . (24)
. (24)
Proof by contradiction.
In general, due to axiom I it is
![]() . (25)
. (25)
According Equation (23), we obtain
![]() . (26)
. (26)
Due to Equation (17) we find then straightforwardly that
![]() . (27)
. (27)
Heisenberg himself did not defined his uncertainty principle as either ![]() or as
or as ![]() but as
but as![]() . By contrast, it is important to note that Heisenberg’s uncertainty principle is characterized by using the same term
. By contrast, it is important to note that Heisenberg’s uncertainty principle is characterized by using the same term ![]() and not two different terms like
and not two different terms like ![]() and
and ![]() as the generally valid definition of Heisenberg’s uncertainty principle. Thus far, let us follow strictly Heisenberg himself is his own line of thought. Rearranging Equation (27), we obtain
as the generally valid definition of Heisenberg’s uncertainty principle. Thus far, let us follow strictly Heisenberg himself is his own line of thought. Rearranging Equation (27), we obtain
![]() . (28)
. (28)
Dividing Equation (28) by Heisenberg’s term (![]() ), it is
), it is
![]() . (29)
. (29)
Finally, Heisenberg’s uncertainty principle demands that
![]() . (30)
. (30)
Quod erat demonstrandum.
4. Discussion
It is appropriate to mark that the historical development of algebraic notations is characterized by a progressive introduction of symbols and the elimination of non mathematical verbal expressions. For instance, the historical development of algebraic equations and algebraic inequalities is associated with names like Robert Recorde, Thomas Harriot and other too. As a matter of fact, let us note that Robert Recorde (ca. 1512 - 1558), a Welsh mathematician and physician, initiated in 1557 [4] our symbol for algebraic equations as “=”. The symbol “<” for the strict inequality to mean “is less than” and the symbol “>” for the strict inequality to mean “is greater than” was devised by Thomas Harriot 1631 in his book Artis analyticae praxis ad aequationes algebraicas nova expedita et generali methodo resolvendas [5] [6] . Thus far, the notions and the meaning of equalities and inequalities are well known and clear since centuries.
Under some certain circumstances Heisenberg’s uncertainty principle defined as ![]() is already refuted. This non-strict inequality changes to
is already refuted. This non-strict inequality changes to![]() . Especially under conditions where σ(p) = 0 we obtain
. Especially under conditions where σ(p) = 0 we obtain ![]() and at the end +0 ≥ +1, which is a contradiction [8] . The purpose of this paper is to refute Heisenberg’s uncertainty principle under any circumstances. Consequently, Heisenberg’s uncertainty principle is based on an assumption which produces dichotomies and giving us the impression that the options presented by Heisenberg himself are mutually exclusive of each other. Heisenberg is presenting only two options out of a spectrum of possible choices, more just does not exist. In last consequence, Heisenberg restricts the relationship between position and momentum to a situation in which only limited and completely different alternatives are considered and forces us to make a choice. Thus far, due to Heisenberg’s understanding to the relationship between position and momentum we must accept that
and at the end +0 ≥ +1, which is a contradiction [8] . The purpose of this paper is to refute Heisenberg’s uncertainty principle under any circumstances. Consequently, Heisenberg’s uncertainty principle is based on an assumption which produces dichotomies and giving us the impression that the options presented by Heisenberg himself are mutually exclusive of each other. Heisenberg is presenting only two options out of a spectrum of possible choices, more just does not exist. In last consequence, Heisenberg restricts the relationship between position and momentum to a situation in which only limited and completely different alternatives are considered and forces us to make a choice. Thus far, due to Heisenberg’s understanding to the relationship between position and momentum we must accept that
![]() . (31)
. (31)
As a matter of fact, according to Heisenberg’s uncertainty principle, we must adequately take into account that the strict inequality
![]() (32)
(32)
explains the relationship between position and momentum in a logical and mathematically consistent way, too. Both forms of the mathematical formulation of the relationship between position and momentum are equally valid. Due to Heisenberg’s understanding of the relationship between position and momentum, if a measurement is performed and if it is found that
![]() (33)
(33)
then it is equally found that it is not the fact that
![]() (34)
(34)
and vice versa. Further, following Heisenberg’s logic, we ever obtain either
![]() (35)
(35)
or
![]() . (36)
. (36)
In particular, let us now analyze the result of our theorem in more detail. However, Heisenberg generalizations are not as straightforward as Heisenberg suggested. In particular, it is possible to transfer a strict inequality into equality and vice versa [7] . Finally, on a more formal level, we note according to Equation (29) that Heisenberg’s uncertainty principle forces us to accept that
![]() (37)
(37)
which is a logical contradiction. Thus far, it is possible to derive a logical contradiction out of Heisenberg’s uncertainty principle. In the same respect, Heisenberg himself does not accept logical contradictions at all. In his 1927 paper Heisenberg demands that “Eine physikalische Theorie… niemals innere Widersprüche enthält” [1] . In broken English: “a physical theory… should never contain inner contradictions”. Altogether, it appears very difficult to convince the majority of the scientific community that our world is grounded on the equation +0 = +1. On the one side, Heisenberg does not accept logical contractions at all [1] , on the other side Heisenberg’s uncertainty principle leads straightforward into a logical contradiction. Heisenberg is contradicting himself in the same paper and has refuted himself too. As generally known, Einstein has never accepted Heisenberg’s uncertainty principle as a fundamental law of objective reality and as we have demonstrated, rightly too. However, Einstein was not able to provide a formal refutation of Heisenberg’s uncertainty principle. Einstein died in 1955 but his position on Heisenberg’s uncertainty principle remained unchanged until the end of his life. Again, Heisenberg failed to get Einstein’s endorsement for his uncertainty principle as a dramatic breakthrough in our basic understanding of the foundations of objective reality. Einstein was right on this point. As we have seen, Heisenberg’s uncertainty principle leads to a contradiction and is based on a contradiction. Consequently, Heisenberg’s uncertainty principle is refuted in general. Especially, Heisenberg has not refuted the principle of causality.
5. Conclusion
Heisenberg’s uncertainty principle has been already refuted for several times [8] [9] . Meanwhile, Anti Heisenberg provides a new and very simply proof and marks the beginning of the end of Heisenberg’s uncertainty principle, ultimately.