Financial Time Series Modelling of Trends and Patterns in the Energy Markets ()
Received 14 February 2016; accepted 20 May 2016; published 23 May 2016

1. Introduction
Energy use is behind virtually everything a person comes into contact with. The energy industry has rapidly expanded and become increasingly interdependent. In developed economies, the increase in energy consumption indicates a reliance on energy and its related products for continued and sustainable economic growth and development. Developing economies also rely on the development of energy resources to drive their growth. Energy was once viewed just as a utility, and an enabler with limited consumer interest, but now, it is key in the struggle for sustainable future economic growth [1] [2] .
Energy prices, which are largely linked to oil prices, are a major concern for most economies. The recent financial crises and their ripple effects and after shocks have been largely unprecedented in terms of timing, speed and magnitude of impact on the world economies. Forecasting of crude oil prices is important for better investment and risk management and policy development, and econometric models are the most commonly used. Various authors have employed time series [3] [4] , financial [5] and structural models [6] in forecasting crude oil prices. Financial studies involve asset returns [7] - [9] , instead of prices, since, firstly, returns give a complete and scale-free summary of the investment opportunities and secondly, return series have nice statistical pro- perties known as stylised facts. These properties have important implications in model selection. Some of these interesting phenomena include volatility clusters which relate to the observation that the magnitudes of volatili- ties of financial returns tend to cluster together [9] [10] , the leverage effect which relates to the asymmetry of news impact [11] , leptokurticity, calendar effects and non-linear dependence.
In this paper, we regard an observed price series,  as a particular realisation of a stochastic process
as a particular realisation of a stochastic process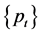 . Standard time series analysis rests on important concepts such as stationarity, ergodicity, auto-
. Standard time series analysis rests on important concepts such as stationarity, ergodicity, auto-
correlation, white noise, innovation, and on a central family of models, the autoregressive moving average (ARMA) models [12] [13] . A stationary time series can be usefully described by it’s mean, variance and autocorrelation or spectral density function [12] [14] , and the joint probability distribution of any two observations, say, 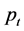 , and
, and 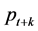 is the same for any two time periods t and
is the same for any two time periods t and 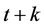 separated by the same lag k [15] . For an ergodic process, we need not observe separate independent replications of the entire process in order to estimate its mean value or other moments [16] .
separated by the same lag k [15] . For an ergodic process, we need not observe separate independent replications of the entire process in order to estimate its mean value or other moments [16] .
In addition to the ARMA models, for the analysis of financial time series, we introduce the concept of volatility, which is pivotal in finance. Along side volatility we also consider the main stylised facts concerning financial time series [8] [13] [17] . In order to capture these stylised facts, we fit the autoregressive conditional heteroscedastic (ARCH) model first developed by Engle [18] and later generalized by Bollerslev [19] to generalised autoregressive conditional heteroscedastic (GARCH) model. A GARCH model is a parametric error distribution, which does not only capture volatility clustering but also accommodates some of the thick tails commonly found in financial time series.
This paper details the empirical analysis of financial time series data. We consider the official daily prices from the trading floor of the New York Mercantile Exchange (NYMEX) for a specific delivery month for Cushing Oklahoma West Texas Intermediate (OK WTI), Reformulated Blendstock for Oxygenate Blending (RBOB), and the number 1 heating oil futures contracts at close of business at 2:30 p.m. We begin the analysis from model identification, selection, estimation, diagnostic checking and finally forecasting. The analysis is done using MATLAB [20] . The rest of the paper is organized as follows: Section 2 discuses the methods used in empirical analysis, Section 3 gives a brief discussion of the data used, and the empirical analysis and the results obtained and finally Section 4 gives a summary of the work and the findings.
2. Methodology
2.1. Models
The full model under consideration falls under the general class of the combined 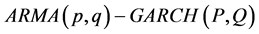 models which include an ARMA specification in the conditional mean and a GARCH specification in the conditional variance. The application of
models which include an ARMA specification in the conditional mean and a GARCH specification in the conditional variance. The application of  model is a common approach in time series analysis that considers autocorrelation, volatility clustering, and heteroscedasticity. This class caters for
model is a common approach in time series analysis that considers autocorrelation, volatility clustering, and heteroscedasticity. This class caters for
models with constant variance under the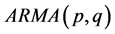 , and heteroscedastic models under the
, and heteroscedastic models under the .
.
If  denotes the price series at time t, let
denotes the price series at time t, let 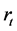 be the log-return, and
be the log-return, and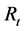 , the relative or simple return so that
, the relative or simple return so that
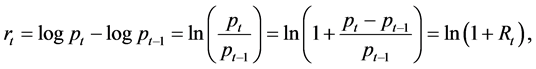 (1)
(1)
an  model for the log-return series
model for the log-return series , is specified as follows:
, is specified as follows:
![]() (2)
(2)
When![]() , the model reduces to an
, the model reduces to an![]() . Other sub-models can be deduced depending on the respective values of the parameters
. Other sub-models can be deduced depending on the respective values of the parameters![]() .
.
2.2. Model Identification, Parameter Estimation and Model Selection
We start with an exploratory analysis of the price data to establish if the set of properties, common across many stocks, in many markets over time periods, that have been observed by many studies [7] [8] [17] are present. We examine spot and futures prices for these stylised facts and other statistical properties such as stationarity. We analyse the descriptive statistics and test for normality using the Jarque-Bera (JB) test [21] .
To test for stationarity, the Dickey-Fuller (DF) test [22] is employed. If the data is non-stationary, dif- ferencing is performed until stationarity is achieved. Once stationarity is established, we study the autocorre- lation function (ACF) and partial autocorrelation function (PACF) in order to determine the form of the
![]() model for each series. A set of candidate models, around this initial model are then identified for further comparison.
model for each series. A set of candidate models, around this initial model are then identified for further comparison.
Once the models for the conditional mean and variance have been identified from the differenced series, we employ the maximum likelihood estimation (MLE) method to fit parameters for the specified model of the dif- ferenced series.
The final model for each series is then selected based on Akaike’s Information Criterion (AIC) which measures of goodness of fit or uncertainty for the range of values of the data. It measures the difference between a given model and the “true” underlying model. AIC is a function of the squared sum of errors (SSE), number of
observations n, and the number of independent variables ![]() where k includes the intercept, and is calculated as
where k includes the intercept, and is calculated as![]() . The best model is the one with the smallest AIC.
. The best model is the one with the smallest AIC.
2.3. Forecasting
Model selection does not depend only on the goodness-of-fit of a model to the data, but also on the objective of the analysis. A model that is best in the in-sample fitting will not necessarily provide more accurate forecasts [8] . For this reason, it is common to use the performance of out-of-sample forecasts to aid in the selection of an adequate statistical model.
The forecasting ability of the model can only be determined by considering how well a model performs on data not used in estimating the model. It is common practice to partition the data into two sets, use the larger portion for estimating the model and the smaller one for testing the model. The test data can be used to measure model accuracy on new data. The size of the test data set should typically be about 20% of the total sample, although this depends on the sample size and the forecast horizon. In an ideal sense, the size of the test sample should be at least as large as the maximum forecast horizon required [23] .
The sample standard deviation, ![]() of return is used as a simple forecast of volatility of returns,
of return is used as a simple forecast of volatility of returns, ![]() , over the future period
, over the future period![]() . The k-days period historical variance is calculated as
. The k-days period historical variance is calculated as![]() , where the sample mean return
, where the sample mean return![]() , is the estimate of the mean return
, is the estimate of the mean return![]() . In most cases, the mean is usually set to zero in order to get a better forecast. Multiplying the variance by N, the number of trading days in a year and taking the square root gives the annualised volatility
. In most cases, the mean is usually set to zero in order to get a better forecast. Multiplying the variance by N, the number of trading days in a year and taking the square root gives the annualised volatility![]() . The number of trading days in a year is taken to be
. The number of trading days in a year is taken to be![]() .
. ![]() is the best estimator for the volatility from the available price data and the volatility of any period of length, k, can be estimated from it.
is the best estimator for the volatility from the available price data and the volatility of any period of length, k, can be estimated from it.
The k-day volatility forecast can also be found by using the GARCH model. Under the condition that returns are uncorrelated across days, the k-day variance as of ![]() is given by
is given by
![]() (3)
(3)
The volatility forecast over the future period from ![]() to
to![]() , denoted by
, denoted by![]() , is an average of the expected volatility on each day from t to
, is an average of the expected volatility on each day from t to ![]() i.e.
i.e.
![]() (4)
(4)
where
![]() (5)
(5)
Note that if![]() ,
,
![]() (6)
(6)
which is the unconditional variance.
In-sample and out-of-sample forecasting ability of models can be measured using the mean absolute error (MAE) and root mean squared forecasting errors (RMSFE) which measures the out-of-sample losses. The RMSFE assigns greater weight to large forecast errors. This fact is handled using the MAE which on the contrary assigns equal weights to both over and under predictions of volatility.
The realised volatility at each forecast date is calculated from the expression![]() , so that, if the forecast volatility is
, so that, if the forecast volatility is![]() , the RMSFE for a model is given by
, the RMSFE for a model is given by ![]() and the MAE is given by
and the MAE is given by ![]() where n and s denote the number of forecasts and the set of times at which ex-ante forecasts are produced respectively in the above expression.
where n and s denote the number of forecasts and the set of times at which ex-ante forecasts are produced respectively in the above expression.
Forecasting using GARCH models is obtained recursively [24] . If we left t be the forecast origin, then, the k- step ahead forecast for ![]() is
is
![]() (7)
(7)
An alternative way of writing Equation (7) is as shown in Equation (8)
![]() (8)
(8)
where
![]()
From Equation (8), we can see that ![]() as
as ![]()
3. Data and Results
This paper investigates the trends and patterns of return series for spot and futures prices of Cushing OK WTI, RBOB and the number 1 heating oil traded in the NYMEX, for the period running from 2nd January 2006 to 22nd May 2015. The data was obtained from the US Energy Information Administration (EIA) website http://www.eia.gov/petroleum/data.cfm, accessed on June 25, 2015. The US EIA is the statistical and analytical agency within the US Department of Energy. It is the principal agency of the US Federal Statistical System responsible for collecting, analysing, and disseminating energy information to promote sound policy-making, efficient markets, and public understanding of energy and its interaction with the economy and the environment. EIA is the premier source of energy information in the US and, by law, its data, analyses, and forecasts are independent of approval by any other officer or employee of the US government. [25] .
Figure 1 shows various series plots for daily spot and futures prices for Cushing OK WTI, RBOB gasoline
![]()
Figure 1. Time series plots for spot, futures prices and crack spreads in energy markets. CF = crude futures, CS = crude spot, GF = gasoline futures, GS = gasoline spot, HF = heating futures and HS = heating spot.
and No. 1 heating oil traded at the NYMEX. The data appears non-stationary, with occasional jumps and spikes indicating heteroscedasticity. Testing the price series for stationarity using DF test shows that they all contain unit roots.
Table 1 gives a summary of the descriptive statistics and results for the JB test for the differenced price series. From the measure of skewness, all the series except the crude spot are skewed to the left. These series exhibit positive excess kurtosis, and these are some of the stylised facts observed in financial time series data. Based on the p-values of the JB test, we reject the null hypothesis of normality for all the differenced series.
Figure 2 shows plots of the differenced crude futures and spot prices. The series appear mean stationary but are not variance stationary. Volatility clustering, jumps and spikes are also observed.
We employ the DF test for stationarity on the differenced series. This is a one-sided left tail test and Table 2 gives the summary report of the DF test on the six series. Stationarity is confirmed for all these series, and hence they can be subjected to further time series analysis
Figure 3 and Figure 4, show the ACF and PACF plots of crude futures and spot price series. From these plots, it is not easy to tell the form of![]() , significant lags are noticed up to lag 39 of the 40 plotted. The same behaviour is exhibited by the other four series. The ACF and PACF fail to identify the form of the model. We proceed to fit several
, significant lags are noticed up to lag 39 of the 40 plotted. The same behaviour is exhibited by the other four series. The ACF and PACF fail to identify the form of the model. We proceed to fit several ![]() models for
models for ![]() and
and![]() , and the one with the smallest AIC is picked. Figure 5 shows a plot of AICs for various models fit for
, and the one with the smallest AIC is picked. Figure 5 shows a plot of AICs for various models fit for![]() , from which we see that the best model is an
, from which we see that the best model is an ![]() with an AIC of −4684.1. This model has the parameters estimated via the maximum
with an AIC of −4684.1. This model has the parameters estimated via the maximum
likelihood, summarized in Table 3. For the crude spot data, the best model is an![]() . A similar analysis was also carried out on the differenced gasoline futures and prices and the results were similar with high orders of autoregressive and moving averages.
. A similar analysis was also carried out on the differenced gasoline futures and prices and the results were similar with high orders of autoregressive and moving averages.
From Table 3, we can use the values of the t-statistic to check the significance of the parameters. The greater the absolute value of t, the greater the evidence against the null hypothesis that there is no significance dif- ference between the parameter estimate and 0. We can use the general rule of thumb that we reject the null
hypothesis whenever![]() .
.
After fitting the ![]() model, we standardized the inferred residuals and checked for normality.
model, we standardized the inferred residuals and checked for normality.
Figure 6 shows two plots. The first one is the residual series which shows a lot of clustering, suggesting non- normality and non-constant variance. The second plot of Figure 6 is a histogram of the residuals also showing evidence of non-normality. Figure 7 shows a quantile-quantile plot and a box plot of the residuals and from these, we can also deduce non-normality of the residuals largely because of the extreme values.
The Kolmogorov-Smirnov (KS) test was employed to check normality of the residuals and the p-value was
![]()
Figure 2. Differenced series for crude futures and spot prices.
![]()
Figure 3. ACF plots for the differenced crude futures and spot price series.
![]()
Table 1. Descriptive statistics for energy spot and futures prices.
D denotes differenced series.
![]()
Figure 4. PACF plots for the differenced crude futures and spot price series.
![]()
Figure 5. Plot for the AICs for the various ARMA models fitted for the differenced crude futures price data.
![]()
Table 2. Results from the Dickey-fuller test on the six series.
![]()
Figure 6. Normality plots for residual checks.
![]()
Figure 7. QQ-plot and Box plot for residuals from the ARMA(6, 11) model.
![]()
Table 3. Results from the ![]() Model fitted to the differenced crude futures price series.
Model fitted to the differenced crude futures price series.
found to be <0.001 implying the residuals are not normally distributed. In this case the ![]() does not conform to the assumption normality in the innovations.
does not conform to the assumption normality in the innovations.
The Ljung-Box (LB) test on the residual series resulted in a p-value of 0.9781 indicating the residuals are not autocorrelated. Based on these results, we test for ARCH effects in the squared residuals using the LB test and obtained a p- value <0.001, indicating significant ARCH effects in the residuals.
Figure 8 also shows evidence of serial autocorrelation on the squared residuals. The PACF plot shows autoregression of order one so ![]() should capture the ARCH effects in the residuals.
should capture the ARCH effects in the residuals.
We then specify a combined ARMA-GARCH model to capture the ARCH effects. Fitting a ARMA(6,11)- GARCH(1,1) had an AIC of 8810.9. However, a search for the best combined model revealed that an ![]() model gave the best fit with an AIC of −4.4037. From this analysis, we see that a more appropriate model to use would be one with a constant conditional mean and a conditional variance.
model gave the best fit with an AIC of −4.4037. From this analysis, we see that a more appropriate model to use would be one with a constant conditional mean and a conditional variance.
The analysis shows the differenced series exhibit “stylised facts” typically seen in high frequency financial data. volatility clustering manifests itself as autocorrelation in squared and absolute returns, or in the residuals of the estimated conditional mean equation. Examining the ACF and PACF plots for the squared differenced series shown in Figure 9 and Figure 10, reveal serial correlation of the squared differenced series. Gasoline and heating oil series exhibit the same behaviour.
The significance of these autocorrelations at various lags was tested using the LB test and the Lagrange multiplier (LM) test at lags 1, 5 and 10, and the results are summarized in Table 4. As is evident, there is enough evidence to reject the null hypothesis of no ARCH effects as per the LB test since the test indicates that there are significant ARCH effects in the all squared series. However, based on Engle’s ARCH test, which is the LM test, we do not have sufficient evidence to reject the hypothesis of no ARCH effects for the gasoline futures and the heating oil futures series. For all the other series we reject that hypothesis of no ARCH effects.
Serial correlation in squared returns, or conditional heteroscedasticity can be modelled using GARCH models. GARCH models allow for the volatility to evolve with time. A GARCH model can be expressed as an ARMA model of squared residuals and hence many of it’s properties follow easily from those of the corresponding ARMA process. If the fourth order moment of a GARCH (1,1) exists, the kurtosis implied by a GARCH (1,1) process with normal errors is greater than that of the normal distribution which is 3 [19] . For this reason, a GARCH model with normal errors can replicate some of the fat tailed behaviour observed in financial time series, though, most often, a GARCH model with a non-normal error distribution is required in order to fully capture the observed fat tail behaviour in financial time series.
![]()
Figure 8. ACF and PACF for squared residuals from the ARMA(6,11) model.
![]()
Figure 9. ACF plots for the squared differenced crude futures and spot price series.
![]()
Figure 10. PACF plots for the squared differenced crude futures and spot price series.
We fit several ![]() model to the differenced crude futures series for
model to the differenced crude futures series for![]() . We estimate the parameters
. We estimate the parameters![]() ,
, ![]() and
and ![]() of the
of the ![]() model and the in-sample estimates of the volatility. The Matlab command garch, models the return series as
model and the in-sample estimates of the volatility. The Matlab command garch, models the return series as ![]() and estimates the parameters
and estimates the parameters![]() ,
, ![]() and
and ![]() via maximum likelihood.
via maximum likelihood.
For the differenced crude futures series, the model with the smallest AIC was GARCH (19, 16) with an AIC of 8776.4 as shown in Figure 11 which shows the AICs of all the models fitted. The best model according to these fits have the parameters summarized in Table 5.
![]()
Figure 11. A plot for the AICs for various GARCH models fitted.
![]()
Table 4. Results from the Ljung-Box test and LM test for ARCH effects on the squared differenced series.
p-values are indicated in the parenthesis.
From these results, it can be seen that most of the in-between lags are not significant, the most important lags at 16 and 19. An analysis on the residuals of this model show that this model gives a fairly good fit. As per the AIC values, most these models do not seem to be significantly different and so the lags may be reduced to gain parsimony. An examination of the plots of the standardised residuals after fitting the GARCH(1,1) model for the return series indicates that the residuals are, on the overall, stable with some clustering. The standardised residuals exhibit no residual autocorrelation. It therefore makes more sense just to fit a ![]() for this data.
for this data.
The other series also behave in much the same way as the crude futures. Fitting a ![]() model on all the six series gives the results in Table 6. From the measure of persistence, we see the highest persistence of 0.9938 in the
model on all the six series gives the results in Table 6. From the measure of persistence, we see the highest persistence of 0.9938 in the ![]() series, although, all other return series are quite persistent. This indicates that the volatility
series, although, all other return series are quite persistent. This indicates that the volatility
![]()
Table 5. Results from the ![]() model fitted to the differenced crude futures price series.
model fitted to the differenced crude futures price series.
![]()
Table 6. Results from the ![]() model fitted to all the differenced price series.
model fitted to all the differenced price series.
(![]() ) measures the persistence.
) measures the persistence.
processes return to their means after some time. The implication of this high persistence is that these shocks have a significant effect on the prices in these markets.
Forecasting
The total length of the data under consideration is 2363 data points. This data set was divided into two sets, the first sub-sample, used for training the model contained 2063 points and the second one, used for testing, con- tained 300 points.
In order to regain a forecast of the price series, the differencing on the forecast series obtained from the forecasts of the inferred conditional variances is undone. However because the inferred variances are con- ditioned on a standard normal error, there are several possibilities and, having many different forecasts and averaging would give a stable forecast for the crude futures prices, which can then be used to predict future crude oil futures prices. In Figure 12, we see one of the possibilities of the forecast prices. The RMSFE for this model is 0.2072, an indication that the forecasts are generally good.
![]() Time in years
Time in years
Figure 12. Crude futures price series showing foretasted prices.
4. Discussion
This paper employs statistical and econometric techniques to investigate and model financial time series trends in energy markets. To do this, daily closing prices for a period of about 10 years for Cushing OK WTI, RBOB and number 1 heating oil spot and futures contracts traded in the NYMEX are considered. The paper also investigates the existence of stylised facts in these series, in order to fit an appropriate model that adequately describes the market dynamics.
Price data are tested for stationarity using the DF test and results show the existence of unit roots. Normality is tested for using the JB test and non-normality is established. Return series are then generated from the price series through differencing, and then tested for stationarity using the DF test. The results reveal that return series are indeed mean stationary, but are definitely not variance stationary. Several ARMA models are fit to the return series and the standardised residuals analysed. For the crude futures return series, the best model turns out to be
an ![]() an for the crude spot it is an
an for the crude spot it is an ![]() among others, based on their AICs. These resultant models however contravene the Gaussian innovation assumption.
among others, based on their AICs. These resultant models however contravene the Gaussian innovation assumption.
We then propose a combined ![]() model to capture the ARCH effects in the variance, then find that the best model under these circumstances is the
model to capture the ARCH effects in the variance, then find that the best model under these circumstances is the![]() , implying a constant mean conditional variance equation. We finally find that for example, for the crude futures return series, the
, implying a constant mean conditional variance equation. We finally find that for example, for the crude futures return series, the ![]() is the best model based on the AIC, although a
is the best model based on the AIC, although a ![]() does quite well for
does quite well for
this and all the other six series with the residual analysis conforming to the assumption of Gaussian Innovations. GARCH models can therefore adequately model the trends and patterns in the energy markets. The trends also depict time varying variability and high persistence of oil price shocks. These shocks therefore have a significant impact on the prices of these energy prices.