Received 31 March 2016; accepted 15 May 2016; published 18 May 2016

1. Introduction
Studies on trade policy, which progressed by paying attention to strategic interaction between governments and firms (Brander and Krugman (1983) [1] , Brander and Spencer (1984) [2] , etc.), have entered a new stage since Handley (2014) [3] , Handley and Limao (2015) [4] etc. raised the problem of optimal start time of export to show successfully that uncertain trade policy delays exporters’ entry into new markets, by making use of optimal stopping theory that has been used to develop strategies on timing in a stochastic economy since McDonald and Siegel (1986) [5] demonstrated the value of waiting, followed by Dixit (1989) [6] , Farzin, Huisman and Kort (1988) [7] and so on. The present paper attempts to push forward these studies by combining the optimal stopping theory with the standard microeconomics-based trade theory, as well as by extending Fujita (2007) [8] that examined the optimal timing of export by assuming a small country where firms can export as much as it wishes at the world price. More precisely, by incorporating product demand functions explicitly into the optimal stopping trade model, we construct a two country model to reveal the relationship between the trade policy uncertainty and the optimal start time of export.
Structure of this paper is as follows. After constructing a basic model to derive the equilibrium profit of exporting firm in Section 2, section 3 formulates the objective function of the exporting firm. Based on these analyses, in section 4 we demonstrate the relationship between the trade policy uncertainty and the start time of export, followed by the welfare implication of the backfiring effect in Section 5. Concluding remarks are made in section 6.
2. Basic Model
Let us consider an inter temporal economy where time passes continuously with importance of the future diminishing with discount rate ρ. The economy consists of two countries, i.e., domestic and foreign ones, each of which is assumed to have one firm that takes prices as given. 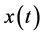 and
and 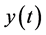 denote the outputs of the domestic firm and the foreign firm in period t, respectively. We assume that the product market is in the foreign country, to which the domestic firm exports its product that is superior to the foreign firm’s product in a sense that the export of the domestic firm’s product reduces the demand for the foreign firm’s product, while the foreign firm’s product makes no effect on the demand for the domestic firm’s product. In order to for mulatethis situation, first of all, we specify the unit price of the domestic firm’s product
denote the outputs of the domestic firm and the foreign firm in period t, respectively. We assume that the product market is in the foreign country, to which the domestic firm exports its product that is superior to the foreign firm’s product in a sense that the export of the domestic firm’s product reduces the demand for the foreign firm’s product, while the foreign firm’s product makes no effect on the demand for the domestic firm’s product. In order to for mulatethis situation, first of all, we specify the unit price of the domestic firm’s product 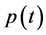 as
as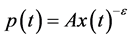 , where A and ε are positive parameters that express market size and elasticity of demand, respectively. As for the foreign firm’s product, we assume that it is “dog” in Boston matrix i.e., its demand is shrinking over time, so the unit price of the foreign firm’s product is given by
, where A and ε are positive parameters that express market size and elasticity of demand, respectively. As for the foreign firm’s product, we assume that it is “dog” in Boston matrix i.e., its demand is shrinking over time, so the unit price of the foreign firm’s product is given by 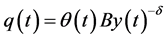 if it were not for the export, where
if it were not for the export, where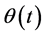 , B and δ are positive parameters that express the degree of market shrinkage, market size and elasticity of demand respectively. We also assume that the domestic firm’s product reduces the willingness to pay for the foreign firm’s product, so as to be expressed as
, B and δ are positive parameters that express the degree of market shrinkage, market size and elasticity of demand respectively. We also assume that the domestic firm’s product reduces the willingness to pay for the foreign firm’s product, so as to be expressed as 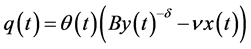 if the amount of the export is
if the amount of the export is , where ν is a positive parameter that expresses the demand-reducing effect of the domestic firm’s product.
, where ν is a positive parameter that expresses the demand-reducing effect of the domestic firm’s product.
We assume that  fluctuates stochastically according as the following geometric Brownian motion,
fluctuates stochastically according as the following geometric Brownian motion,
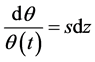 , (1)
, (1)
with initial value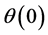 , where s is a positive constant that expresses the uncertainty of the trade policy in a sense that larger s means more uncertain trade policy, while dz is Wiener process that expresses the random movement. Since θ decreases over time in this setting, we assume
, where s is a positive constant that expresses the uncertainty of the trade policy in a sense that larger s means more uncertain trade policy, while dz is Wiener process that expresses the random movement. Since θ decreases over time in this setting, we assume 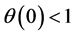 to ensure
to ensure 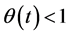 for every t. We also assume that the foreign firm lobbies to its government to levyad valorem tariff on the domestic firm’s product for the protection of its product.
for every t. We also assume that the foreign firm lobbies to its government to levyad valorem tariff on the domestic firm’s product for the protection of its product.
We specify the domestic firm’s average revenue from exporting decreases to 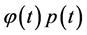 as a result of the foreign government’s protectionist measure, where
as a result of the foreign government’s protectionist measure, where 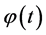 is a parameter that satisfies 0 ≤ φ ≤ 1 to represent the degree of the foreign government’s trade policy in that small
is a parameter that satisfies 0 ≤ φ ≤ 1 to represent the degree of the foreign government’s trade policy in that small ![]() expresses tight trade policy. We assume that the foreign firm lobbies more if its demand shrinks more, i.e.,
expresses tight trade policy. We assume that the foreign firm lobbies more if its demand shrinks more, i.e., ![]() positively relates to
positively relates to ![]() with
with ![]() if
if![]() . In the following, in order to simplify the analysis, we specify
. In the following, in order to simplify the analysis, we specify![]() , to obtain the following geometric Brownian motion,
, to obtain the following geometric Brownian motion,
![]() , (2)
, (2)
with initial value![]() .
.
We assume that the domestic firm incurs a fixed cost of K when starting the export, followed by variable costs of ![]() when producing
when producing ![]() units in period t, where c and η are parameters that satisfy c > 0 and η > 1. Here, entry costs cover the expenses of setting up a distribution network, on-site visits or agency costs and so on as in Handley (2014) [3] and Handley and Limao (2015) [4] . We also assume that the domestic firm optimizes the start time of the export, t*, as well as the amount of the export in each period. As for the foreign firm, for the simplicity of the analysis, we assume that the foreign firm supplies
units in period t, where c and η are parameters that satisfy c > 0 and η > 1. Here, entry costs cover the expenses of setting up a distribution network, on-site visits or agency costs and so on as in Handley (2014) [3] and Handley and Limao (2015) [4] . We also assume that the domestic firm optimizes the start time of the export, t*, as well as the amount of the export in each period. As for the foreign firm, for the simplicity of the analysis, we assume that the foreign firm supplies ![]() amounts of the product in elastically.
amounts of the product in elastically.
Since the domestic firm’s profit in period t, ![]() , is described as
, is described as![]() , we have its first
, we have its first
order condition for the profit maximization as![]() , to yield the equilibrium outputs of the domestic firm in period t as
, to yield the equilibrium outputs of the domestic firm in period t as![]() . By combining this domestic firm’s supply function with the above inverse demand function
. By combining this domestic firm’s supply function with the above inverse demand function![]() , we have the equilibrium output of the domestic firm in period t as
, we have the equilibrium output of the domestic firm in period t as![]() , to obtain the equilibrium profit of the domestic firm in period t as
, to obtain the equilibrium profit of the domestic firm in period t as
![]() where
where![]() . (3)
. (3)
3. Formulation of the Objective Function
From Equation (3), we have its first derivative and second derivative with respect to ![]() as
as ![]() and
and![]() , respectively. Thus, by making use of Ito’s lemma, we can express the stochastic process of the domestic firm’s profit as
, respectively. Thus, by making use of Ito’s lemma, we can express the stochastic process of the domestic firm’s profit as
![]() , (4)
, (4)
where ![]() and
and ![]() with initial value of
with initial value of![]() .
.
By making use of this stochastic process of the domestic firm’s profit, let us express the domestic firm’s objective function to maximize in period 0, ![]() , as a function of φ*, the level of φ in
, as a function of φ*, the level of φ in
period t*. For this purpose, if we let ![]() denote the expected value of one unit of the domestic firm’s profit in period t* (i.e., the expected value of
denote the expected value of one unit of the domestic firm’s profit in period t* (i.e., the expected value of![]() ) as a function of its initial profit
) as a function of its initial profit![]() , the general solution to
, the general solution to ![]() is expressed as
is expressed as
![]() , (5)
, (5)
where γ1 < 0 and γ2 > 0 are solutions to the characteristic equation![]() . Since
. Since ![]() satisfies
satisfies ![]() and
and ![]() where π* is the domestic firm’s profit in period t*, it follows that α = 0 and
where π* is the domestic firm’s profit in period t*, it follows that α = 0 and ![]() where
where ![]() for the simplification of notation, which combined with Equation (5) yields
for the simplification of notation, which combined with Equation (5) yields
![]() . (6)
. (6)
Thus, we can calculate the domestic firm’s objective function to maximize in period 0 as ![]() , which is rewritten as
, which is rewritten as
![]() , (7)
, (7)
by substituting ![]() and
and ![]() into
into![]() .
.
4. Optimal Start Time of the Export
Now, we are ready to determine the domestic firm’s optimal start time of the export.
Since the model of the present paper is stochastic, the optimal timing is expressed by the cut off level of φ*. Therefore, by differentiating Equation (7) with respect to φ* and setting it to zero, we have the domestic firm’s optimal cut off level of φ* as
![]() . (8)
. (8)
If ε < 1, graph of φ* is depicted as a hump-shaped trajectory on s-φ* space with φ*-intercept being ![]() as in Figure 1 with the threshold level of
as in Figure 1 with the threshold level of![]() , which is in sharp contrast with the standard result of the value of waiting that shows φ* decreases monotonically as s increases.
, which is in sharp contrast with the standard result of the value of waiting that shows φ* decreases monotonically as s increases.
Since large s means an increase in the uncertainty of the trade policy and small (large) φ* means postponement (acceleration) of starting of the export, we have the following proposition.
Proposition 1: 1) If the trade policy is less uncertain than a threshold level, an increase in the trade policy uncertainty accelerates the domestic firm’s start time of the export; 2) if the trade policy is more uncertain than a threshold level, however, an increase in the trade policy uncertainty postpones the domestic firm’s start time of the export.
In the present model, as Equation (3) shows, an increase in the trade policy uncertainty pulls up the growth rate of the domestic firm’s profit, to accelerate the start time of the export. If this accelerating effect surpasses the standard postponing effect caused by the value of waiting, overall effect accelerates the start time of the export, which we define here as a stochastic version of the backfiring effect that was shown by Ishikawa and Lee (1997) [9] in vertically related deterministic markets.
If![]() , on the other hand, graph of φ* is depicted as a decreasing graph on s-φ* space as in Figure 2, showing that increase in the trade policy uncertainty delays the start time of the export, which is consistent with the typical case in the optimal stopping model.
, on the other hand, graph of φ* is depicted as a decreasing graph on s-φ* space as in Figure 2, showing that increase in the trade policy uncertainty delays the start time of the export, which is consistent with the typical case in the optimal stopping model.
![]()
Figure 1. Hump-shaped relationship between uncertainty and the timing of export.
![]()
Figure 2. Negative relationship between uncertainty and the tim- ing of export.
5. Welfare Implication of the Backfiring Effect
We can derive the welfare implication of the stochastic version of the backfiring effect, i.e., how the export triggered by the trade policy uncertainty makes effect on the world welfare which we define as sum of the surpluses of the two countries.
For this purpose, let us first assume that firms’ costs are payment for the labor and capital the households provide, so that they are canceled out in calculating the welfare. Since the tariff revenue is also canceled out, the world welfare in period t without exporting, ![]() , is defined as the consumers’ surplus from the foreign firm’s product as
, is defined as the consumers’ surplus from the foreign firm’s product as
![]() . (9)
. (9)
When the domestic firm exports, on the other hand, the world welfare in period t, ![]() , is defined as sum of the consumers’ surpluses from both firms’ products, which is calculated as
, is defined as sum of the consumers’ surpluses from both firms’ products, which is calculated as
![]() . (10)
. (10)
By comparing (9) and (10), we have![]() , i.e., the export enhances the world welfare if
, i.e., the export enhances the world welfare if ![]() ;
;![]() , i.e., the export reduces the world welfare if
, i.e., the export reduces the world welfare if![]() .
.
Since the φ*-intercept in Figure 1 is![]() , we see that the backfiring effect reduces the world welfare if
, we see that the backfiring effect reduces the world welfare if![]() , which is simplified as
, which is simplified as ![]() , to obtain the following proposition.
, to obtain the following proposition.
Proposition 2: Backfiring effect reduces the world welfare if ![]() .
.
This proposition demonstrates that the stochastic version of the backfiring effect reduces the world welfare if the demand for the exported products are low (A is small), starting the export is costly (K is large) or the future is not important (ρ is large) and so on.
6. Conclusions
We began this research wishing to invent anew framework that combines the optimal stopping theory with the standard microeconomics-based trade theory. Our result was more surprising than we had expected: if the trade policy is less uncertain than a threshold level, an increase in the trade policy uncertainty accelerates the domestic firm’s optimal start time of the export, which was missed in the previous studies that did not formulate the demand structures explicitly. We also revealed that such a stochastic version of the backfiring effect reduces the world welfare if the demand for the exported products is low, starting the export is costly or the future is not important.
We truly hope this research note, which sheds new light on the problem of the optimal start time of the export, will contribute to the progress of studies on international economics.