Spherical Gravitational Collapse of Anisotropic Radiating Fluid Sphere ()
Received 22 March 2016; accepted 15 May 2016; published 18 May 2016

1. Introduction
In order to construct the new realistic models, it is desirable to solve the Einstein's field equations but due to non linear character of the equations it is a very difficult task; various efforts have been made in this direction. The maiden exact solution of spherical gravitational collapse was due to Oppenheimer and Snyder [4] and which apparently suggested that such a collapse results in formation of Black Holes. Taking into account the outgoing radiation from collapsing spherical fluid Vaidya [5] [6] initiated the problem describing the exterior field and Santos [7] presented the junction conditions of collapsing spherically symmetric shear-free non-adiabatic fluid with radial heat flow.
Herrera and Santos [8] and Mitra [9] established the fact that gravitational collapse is a high energy dissipating process which plays a dominant role in the formation and evolution of stars. Historically the dissi- pation of energy from collapsing fluid distribution is described in two limiting cases. The first case describes the free streaming approximation (pure radiation) while second one is diffusion approximation (heat flow). The prominent work in pure radiation is due to Tewari and he solved the Einstein’s field equations with a new approach and developed the Quasar models [10] - [13] . While a number of realistic models in diffusion approximation with the impact of various factors such as inhomogeneity, anisotropy, viscosity, electromagnetic field and various dissipative processes on the evolution are critically discussed by de Oliveira et al. [14] ; Bonnor et al. [15] ; Herrera et al. [16] ; Maharaj and Govender [17] ; Ivanov [18] ; Tewari [19] [20] ; Pinheiro and Chan [21] ; Tewari and Charan [22] [23] ; Sharif and Iftikhar [24] .
Bowers and Liang [25] did the pioneering work in the field of anisotropic fluid models which enabled researchers to study the effect of anisotropy on the physical behavior of a star undergoing gravitational collapse. Herrera and Santos [26] explored the properties of anisotropic self-gravitating spheres using the perturbation method. Herrera et al. [27] investigated that the local pressure anisotropy is one of the responsible factors for inhomogeneities in energy density and in this series some interesting noticeable work is reported by Ivanov [28] [29] ; Reddy et al. [30] ; Tewari and Charan [31] [32] ; Govender et al. [33] and a different approach with a new concept Horizon function is very recently introduced for anisotropic fluids by Ivanov [34] [35] .
The main objective of this work is to present a simple anisotropic collapsing radiating fluid model and discuss all the relevant thermal and physical conditions by taking Tewari and Charan [31] solution as seed solution and we propose some new exact solutions for this parametric class of solution which are useful in construction of the compact stars models. The interior metric is spherically symmetric, shear-free, anisotropic radiating away its energy in the form of radial heat and contracting in size during the process of collapse. The interior metric matched with the Vaidya exterior metric [6] over the boundary. Final fate of our model is the formation of a black hole. The paper is organised as: In Section 2 the space-times and the junction conditions for collapsing system are given. In Section 3 solution of Einstein’s field equations is presented. Section 4 describes a parametric class of solution and some new solutions. In Section 5 detailed study of the model in which we have obtained expressions of various physical parameters is described. Section 6 contains the temperature profile of the collapsing body. Finally in Section 7 some concluding remarks have been made.
2. The Space-Times and Junction Conditions
The interior space-time of a shear-free spherically symmetric fluid with the coordinates 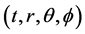 is given by
is given by
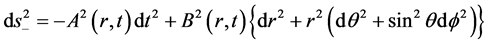 (1)
(1)
The energy-momentum tensor for the matter distribution with anisotropy in pressure is
 (2)
(2)
where  is the energy density of the fluid,
is the energy density of the fluid,  the radial pressure,
the radial pressure, 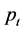 the tangential pressure,
the tangential pressure,  is the four- velocity,
is the four- velocity, 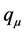 the radial heat flow vector and
the radial heat flow vector and 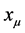 is a unit space like four vector along the radial direction.
is a unit space like four vector along the radial direction.
Assuming comoving coordinates, we have . The heat flow vector
. The heat flow vector 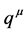 is orthogonal to the velocity vector so that
is orthogonal to the velocity vector so that  and takes the form
and takes the form .
.
Since the interior fluid is radiating energy in the form of heat therefore the exterior space-time of a collapsing radiating star is described by Vaidya’s outgoing exterior metric [6]
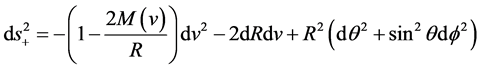 (3)
(3)
where v is the retarded time and 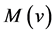 is the Vaidya mass.
is the Vaidya mass.
The junction conditions for radiating star matching two line elements (1) and (3) at the boundary continuously across a spherically symmetric time-like hyper surface ![]() are very well known and given by Santos [7]
are very well known and given by Santos [7]
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where ![]() is the mass function calculated in the interior at
is the mass function calculated in the interior at ![]() (Cahill et al. [36] ; Misner and Sharp [37] ). The primes and dots stand for differentiation with respect to r and t respectively.
(Cahill et al. [36] ; Misner and Sharp [37] ). The primes and dots stand for differentiation with respect to r and t respectively.
Some other physical and thermal features of the collapsing matter are the surface luminosity and the boundary redshift ![]() observed on
observed on ![]() are
are
![]() (7)
(7)
![]() (8)
(8)
The total luminosity for an observer at rest at infinity is
![]() (9)
(9)
3. Solution of Einstein’s Field Equations
In order to solve the Non-trivial Einstein’s field equations which are generated by (1) and (2), we choose a separable form of the metric coefficients given in (1) into functions of r and t coordinates as ![]() and
and![]() . The coupling constant in geometrized units is taken as
. The coupling constant in geometrized units is taken as ![]() and in view of (1) and (2) with the help of separable metric coefficients we get the following expressions for field equations
and in view of (1) and (2) with the help of separable metric coefficients we get the following expressions for field equations
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
where
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Here the quantities with the suffix 0 corresponds to the static star model with metric components![]() .
.
In the absence of non-adiabatic dissipative forces the Equation (5), ![]() , reduces to the condition
, reduces to the condition ![]() and yields at
and yields at ![]()
![]() (17)
(17)
where
![]() (18)
(18)
Tewari [20] by assuming ![]() solved the Equation (17) and the solution so obtained is identical to the solution presented by de Oliveira et al. [14] and Bonnor et al. [15] with
solved the Equation (17) and the solution so obtained is identical to the solution presented by de Oliveira et al. [14] and Bonnor et al. [15] with![]() .
.
![]() (19)
(19)
![]() (20)
(20)
Here we observed that the function ![]() decreases monotonically from the value
decreases monotonically from the value ![]() at
at ![]() to
to ![]() at
at![]() . It interpret that the collapse begins in the remote past and gradually starts evolve into radiating collapse.
. It interpret that the collapse begins in the remote past and gradually starts evolve into radiating collapse.
4. The New Parametric Class of Solution and Some Proposed Solutions
To find a new parametric class of exact solutions of pressure anisotropy equation which is created by the Equa- tions (11) and (12), Tewari and Charan [31] assumed that the anisotropy evolves ![]() and got the following time independent differential equation
and got the following time independent differential equation
![]() (21)
(21)
Making an adhoc relationship between the variables in (21), the above mentioned authors obtained the following solution
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
where ![]() and
and ![]() are constants and
are constants and
![]() (25)
(25)
where n is real if ![]() or
or![]() .
.
For different values of n or l Equations (22) and (23) give a variety of solutions and they are categorized as isotropic pressure and homogeneous density, isotropic pressure and inhomogeneous density while some inhomogeneous density and anisotropic pressure. For ![]() we get the homogeneous density and anisotropic pressure, for
we get the homogeneous density and anisotropic pressure, for ![]() we get the isotropic pressure and homogeneous density and in this case solution reduces to Banerjee et al. [38] and for
we get the isotropic pressure and homogeneous density and in this case solution reduces to Banerjee et al. [38] and for ![]() we get isotropic pressure and inhomogeneous density. In order to maintain the inhomogeniety and anisotropy for a collapsing radiating star, a Horizon-free case has been studied by Tewari and Charan [31] for
we get isotropic pressure and inhomogeneous density. In order to maintain the inhomogeniety and anisotropy for a collapsing radiating star, a Horizon-free case has been studied by Tewari and Charan [31] for ![]() and in an other study the same authors presented a Black hole model for
and in an other study the same authors presented a Black hole model for ![]() [32] . Since a number of solutions can be obtained with the above mentioned parametric class of solution, so keeping this point in mind we here find some exact solutions and listed them in a table and they will be fruitful for further study to construct the various models of radiating and static stars.
[32] . Since a number of solutions can be obtained with the above mentioned parametric class of solution, so keeping this point in mind we here find some exact solutions and listed them in a table and they will be fruitful for further study to construct the various models of radiating and static stars.
5. Physical and Thermal Analysis of a Specific Model
To construct a new relativistic model, in the present study we assume![]() , to maintain the anisotropy for a collapsing radiating star and using (22)-(24) we get
, to maintain the anisotropy for a collapsing radiating star and using (22)-(24) we get
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
The junction condition ![]() gives
gives
![]() (32)
(32)
Here from (30) and (31), we are seeing that at the centre radial and transverse pressures are equal and anisotropy vanishes there.
A physically reasonable solution should satisfy certain energy conditions and they are:
The central values of both the pressures, energy density and gravitational potential should be non-zero positive definite and the solution should have monotonically decreasing expressions for the pressures and density with the increase of r. Thus in view of these conditions, we write the bounds of model parameters ![]() and
and![]() .
.
Now using (10)-(13), (19), (26) and (27) the expressions for ![]() and q reduce the following
and q reduce the following
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
We can see the physical parameters ![]() are finite, positive, monotonically decreasing at any instant with respect to radial coordinate for
are finite, positive, monotonically decreasing at any instant with respect to radial coordinate for![]() .
.
The fluid collapse rate ![]() with the help of (1), (19), (26) and (27) is
with the help of (1), (19), (26) and (27) is
![]() (37)
(37)
where by using (18), (26) and (27) we have
![]() (38)
(38)
The constant ![]() is positive for the given range of the parameters
is positive for the given range of the parameters ![]() and
and![]() .
.
The total energy entrapped inside the surface ![]() is given by using (6), (18), (26), (27) and (38)
is given by using (6), (18), (26), (27) and (38)
![]() (39)
(39)
where
![]() (40)
(40)
Using (4) and (27), we get the physical radius of the collapsing radiating star as
![]() (41)
(41)
Using (7)-(9), (18), (26), (27) and (38) the expressions for the surface luminosity, the boundary redshift on ![]() and the luminosity for distant observer at rest at infinity respectively are
and the luminosity for distant observer at rest at infinity respectively are
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
To obtain the black hole formation time, the surface redshift goes to infinity, for this the term in the parentheses of (44) goes to zero and we have
![]() (45)
(45)
![]() (46)
(46)
6. Temperature Profile for Collapsing Radiating Star
To investigate the temperature inside and on the boundary surface, we utilize temperature gradient law (Israel et al. [39] ; Maartens [40] ; and Martinez [41] )
![]() (47)
(47)
where ![]() is the thermal conductivity and
is the thermal conductivity and ![]() is the relaxation time. To get a simple estimate of the temperature evolution, we set relaxation time as zero in above expression and obtained
is the relaxation time. To get a simple estimate of the temperature evolution, we set relaxation time as zero in above expression and obtained
![]() (48)
(48)
The effective surface temperature observed by external observer can be calculated from the expression (Schwarzschild [42] )
![]() (49)
(49)
where for photons the constant ![]() is given by
is given by![]() , here k and
, here k and ![]() denoting respectively Boltzmann and Plank constants. Choosing
denoting respectively Boltzmann and Plank constants. Choosing ![]() which represents radiation interaction with matter through the diffusive approximation (Misner and Sharp [43] .
which represents radiation interaction with matter through the diffusive approximation (Misner and Sharp [43] .
The arbitrary function ![]() is determined by using (48) and (49) as
is determined by using (48) and (49) as
![]() (50)
(50)
Temperature distribution throughout the interior of the collapsing radiating star is given by
![]() (51)
(51)
It follows that the surface temperature of the collapsing star tends to zero at the beginning of the collapse ![]() and the stage of formation of black hole
and the stage of formation of black hole![]() .
.
7. Conclusion
We here presented a new radiating fluid model collapsing in the influence of its own gravity using Tewari and Charan [31] solution as seed solution. The interior fluid is spherically symmetric shear-free anisotropic and radiating away its energy in the form of radial heat flow. We have obtained a class of exact solutions by assigning different values to the parameter n and proposed solutions are listed in the Table 1. Keeping in mind pressure anisotropy a simple radiating star model for ![]() studied in detail. Physical and thermal features of the model are significantly sound as it corresponds to well-behaved nature for the fluid density, both the radial
studied in detail. Physical and thermal features of the model are significantly sound as it corresponds to well-behaved nature for the fluid density, both the radial
![]()
![]()
Table 1. Parametric class of solutions.
and tangential pressures and the flux density throughout the fluid sphere. We observed that the function ![]() decreases monotonically from the value
decreases monotonically from the value ![]() at
at ![]() to
to ![]() at
at![]() . The apparent luminosity
. The apparent luminosity
as observed by the distant observer at rest at infinity is zero in remote past at the instance when the collapse begins and at the stage of black hole formation.
Particularly we have constructed a radiating star model by taking suitable parameters![]() ,
, ![]() ,
, ![]() ,
,![]() . Initially when
. Initially when ![]() both the mass and physical radius of a core of pre Supernovae were
both the mass and physical radius of a core of pre Supernovae were ![]() and 15.8 km and they remain
and 15.8 km and they remain ![]() and 6.30 km respectively at the time of black hole formation.
and 6.30 km respectively at the time of black hole formation.
The time of black hole formation is observed as 0.62996 S. We observed that the model is well behaved for the chosen constraints and there are a number of such sets for which the solution is well behaved. Thus the parametric class of solution and constructed table is very fruitful for further study of radiating and static compact star’s modeling. The surface temperature of the collapsing radiating star tends to zero at the beginning of the
collapse ![]() and the stage of formation of black hole
and the stage of formation of black hole![]() .
.
Acknowledgements
Authors express their gratitude and thanks to the anonymous referee for his rigorous review and valuable suggestions.