Production in General Equilibrium with Incomplete Financial Markets

Pascal Stiefenhofer

Department of Mathematics, University of Sussex, Brighton, UK.

DOI: 10.4236/jmf.2016.62025                

Abstract

This paper considers a general equilibrium model with incomplete financial markets where production sets depend on the financial decisions of the firms. In the short run, firms make financial choices in order to build up production capacity. Given production capacity firms make profit maximizing production decisions in period two. We provide the conditions of existence of equilibria.

Keywords

General Equilibrium, Incomplete Financial Markets, Production, Existence of Equilibria, Transversality

Received 17 February 2016; accepted 10 May 2016; published 13 May 2016

1. Introduction

Classical general equilibrium literature on production with incomplete markets has focused on variations of the Arrow’s seminal two-period model with exogenous financial assets [1] [2] . In this framework, the firm’s real sequential optimization structure is independent of its financial activities. Firms choose quantities of inputs of production in period one such that associated output choices in period two are optimal. This concept of the firm corresponds to the private ownership model of the firm introduced by Debreu [3] , where the single argument of the firm’s two period sequential optimization function is the real activity vector. In these recent models, in- fluenced by Drèze [4] and Grossmann & Hart [5] , optimality of the choice of a net real activity vector over two periods refers to the average utility of the group of owners of the firm, the stock holders. It is in that sense that the literature has assigned utilities to firms and that the firms’ objective is to maximize some average utility of the share holders. The two concepts applied in most models, slightly differ in the choice of average utility utilized (average utility of initial/final share holders). For a sample of the huge literature applying these concepts see [4] - [8] .

This paper introduces a model of the firm, where its financial and real activities are independent of any average utility of the stock holders. It postulates that firms maximize long run profits and make financial and real decisions sequentially over two periods. The assumption of long run profit maximization is justified by the sequential optimization structure of the firm. Firms issue stocks in period one in order to acquire the cash needed to install production capacity. The optimal quantity of stocks issued by each firm is endogenously determined by the model. Once capacity is installed, after uncertain state of nature has occurred at the beginning of period two, firms produce real goods subject to capacity and technological constraints. The ownership structure introduced in this model eliminates the strategic choice problem of the firm present in the literature. Here, stock holders do not decide about the optimal input vector of the firm in period one. They invest in firms by purchasing stocks in order to transfer wealth across time and between uncertain states of nature. The total quantity of stocks demanded is equal to total quantity of stocks supplied by firms in the same period. The value of total stocks issued by a firm bounds the value of inputs a firm can purchase in period two. Real activities of the firm take place after uncertainty in period two has resolved. These production activities correspond to finding the optimal net activity vector at given prices and revealed state of the world such that profits are maximized at given production capacity.

The sine qua non of the model is then to show that equilibrium exists. It is shown that, for an endogenized price and technology dependent real asset structure, which is transverse to the reduced rank manifolds, equili- brium exists generically in the endowments by the application of Thom’s parametric transversality theorem. Finally, the non-smooth convex production set case is considered, where the piecewise linear production manifolds are regularized by convolution. Existence then follows from the smooth case. Bottazzi [9] demonstrated generic existence of equilibrium for an exchange economy for price dependent smooth assets. Equilibria exist for more general asset structures.

The model is introduced in Section 2. Section 3 shows generic existence for convex smooth production manifolds.

2. The Model

We consider a two period model with uncertainty in period 1 represented as states of nature. An element in the set of mutually exclusive and exhaustive uncertain events is denoted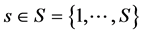, where by

convention 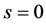represents the certain event in period 0, and S denotes the set of all mutually exclusive uncertain events. This set denotes the overall description of uncertainty in the model, which is characterized by

idiosyncratic and aggregate risk. The general uncertainty space is described by the Cartesian product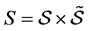. For every production set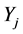, there exists a set of states of nature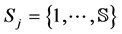, where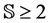, for all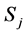. Denote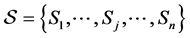, where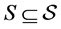, the set of technological uncertain events. At aggregate level there are states of nature. We count in total 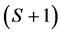states of nature.

The economic agents are the producers and 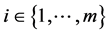consumers which are characterized by sets of assumptions F and C bellow. There are 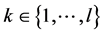physical commodities and financial assets, referred to as stocks. Physical goods are traded on each of the spot markets. Firms

issue stocks which are traded at, yielding a payoff in the next period at uncertain state. The quantity vector of stocks issued by firm j is denoted Other assets such as bonds or options can be introduced without any further difficulties. There are total goods. The consumption bundle of agent i is denoted with and The consumption space for each i is the strictly positive orthant. The associated price system is a collection of vectors represented by with

There are n financial assets traded in period 0. Denote the quantity vector of stocks purchased by consumer i, and denote with associated spot price system

We assume complete commodity markets and model producers’

sequential optimization behavior in an incomplete financial markets environment. Incomplete markets is shown to be a consequence of the technological uncertainty hypothesis. Denote producer j's long run net activity vector

where represents the long run input vector and the associated feasible output vector. A state s net activity of the firm j is denoted where by convention an element denotes a factor of production and a good produced. Let denote the long run net activity vectors.

Sequential behavior of the producers: Consider the sequential structure of the optimization problem of the firm. Firms build up long run production capacity in the first period, for that, they issue stocks. The value of

total stocks issued in period one, denoted where is a real number, bounds the quantity of goods a producer j can buy in state at input prices in period two. Once money is received

through financial markets, firms install production capacity, and production activities take place subject to constraint long run production sets in the second period. Uncertainty in production is introduced by a random variable for every j. We assume that there are less uncertain states of the world S than financial assets n available for wealth transfer. Hence is out default asumption.

Assumption (T):

For every production set,

Assumption (P):

Firms maximize long run profits.

Assumptions (F):

(i) For each j, is closed, convex, and compact . (ii) For each j, denote a manifold for transformation maps (1) non-linear for all ¹.

Production takes place in the second period, once capacity is installed and state occurred. At firms choose at price q such that long run profits are maximized in every state subject to long run technological feasibility and capacity constraints. Denote the long run production set This set is

not independent of the firm’s technology nor on its financial activities, denoted Z. More formally, the firm’s sequential optimization problem is

(1)

Denote a long run equilibrium output vector associated with the production set boundary Each

firm j is characterized by set of assumptions F (Debreu [3] ). We modify Debreu's assumptions on production sets in order to allow the modeling of endogenous production capacity via financial assets. The maps implied by equation (1), for each state and all producers j define the total long run payoff matrix, a collection of n vectors denoted

(2)

where denotes the technology and capacity dependency of the payoff structure. We next introduce the consumer side of the economy.

The consumer: Each consumer is characterized by set of assumptions C of smooth economies (Debreu [10] ).

Assumptions (C): a) is continuous on and on For each For each for all nonzero hyperplane h such that b) Each i is endowed with.

Consumers want to transfer wealth between future spot markets. For that, they invest in firms in period, receiving a share of total dividend payoffs which are determined in the next period in return. Denote the sequence of budget constraints

(3)

where² ownership structure is a vector defined by the mappings

(4)

where is a positive real number for every is the proportion of total payoff of financial asset j hold by consumer In compressed notation, we write

(5)

where represents the full payoff matrix of order.

We introduce following prize normalization such that the Euclidean norm vector of the spot price system is a strictly positive real number.

Definition 1. A financial markets equilibrium with production satisfies:

a)

b)

c)

d)

a) and b) are the optimization problems of the consumers and producers. c) and d) represent physical goods and financial markets clearance conditions. states that each firm j is owned by the

consumers. We now show that incomplete markets is a consequence of technological uncertainty and then move to the main section of the paper.

Proposition 1 for all j, and

Proof. Let for every j. and Then long run profit prospects imply long run capacity adjustment and market entrance until. Let for every j, and Then, implies market entrance and the issue of new securities such that in the limit as the number of firms by assumption (T). Similar for negative long run profit prospects firms exit the market and □

3. Generic Existence for Convex Smooth Production Manifolds

In this section, we show existence of equilibria. The strategy of the proof is to show that a pseudo equilibrium exists and that every pseudo equilibrium is also a financial markets equilibrium with production. It is known that pseudo equilibria exists for exchange economies. See Duffie, Shafer, Geanokopolos, Hirsh, Husseini, and others [9] [11] - [16] . Genakopolos et al. [8] showed that pseuedo equilibria exist for an economy with production for the case of exogenous financial markets. At variance with their model, where the firm’s problem is to solve a Nash equilibrium, we show that a pseudo equilibrium for a more general price and technology dependent asset structure, permitting the modeling of production and its finance, exists.

Definition 2. if s.t.

then is a no-arbitrage asset price relative to.

Lemma 1. s.t.

Proof. Immediate consequence of the separation theorem for matrices in Gale (1960). It asserts that either such that or such that □

We can now rescale equilibrium prices without affecting equilibrium allocations, let The next step is to derive a normalized no arbitrage equilibrium definition [17] . Let be the gradient

vector from the optimization problem of agent 1, called the Arrow-Debreu agent. The Walrasian budget set for the Arrow-Debreu agent is a sequence of constraints denoted

(6)

For all consumers the no arbitrage budget set consisting of a sequence of constraints is denoted

(7)

where is the span of the income transfer space of period one. Replace with L in where is the Grassmann manifold³ with its known smooth dimensional structure, and L an n-dimensional affine subspace of

Denote the pseudo opportunity set for each i,

(8)

Let be the set of normalized prices, and let be a fixed strictly positive real number. This convenient normalization singles out the first good at the spot as the numeraire. We introduce following definitions for the long run payoff maps associated with sets and:

Definition 3. For any such that let where T denotes the transpose, and (ii) For any such that let , where is a set of matrices A of order.

We can now define the pseudo financial markets equilibrium with production. We then state the relational propositions between a full rank FE with production and a pseudo FE with production.

Definition 4. A pseudo financial markets equilibrium with production satisfies:

a)

b)

c)

e)

e)

Lemma 2. Under assumptions C, demand mappings and for, from argmax a) and b) are. Under assumptions F, supply mappings for from argmax d) are.

Proof. The details of this known result are omitted [11] . However, note that smoothness of demand and supply functions follows from the setup of the model for smooth economies. □

Proposition 2. For every full rank FE with production there exists and a n-dimensional subspace such that is a pseudo FE with production.

Proof. By lemma 1, there exists such that (FE) spot prices at can be rescaled such that then is a equilibrium. Since by definition is of agent 1 at agent 1's consumption bundle is since and.

On the contrary, if have a equilibrium, and such that a), b) c) solves maximization problem for constraints Then by defining every is a equilibrium.

Remark: Since agent 1 faces only the Arrow-Debreu constraints, his behavior is identical in both models.

Observation (2): Suppose are elements of the (FE) pseudo equilibrium manifold, and conditions a) and (ii) hold.

Under these conditions, a consumption bundle is feasible under the constraints b) in the model if and only if is feasible under the constraints holding with equality in a) in the (FE) model.

The next step is then to show that exists. Recall that

Let and Relabel an element of in the orthogonal basis of such that in the neighborhood of, the vector space e is spanned by the columns of a matrix. Similarly, in the neighborhood of, the vector space l in the same orthogonal basis of is spanned by the columns of a matrix. We also rewrite the financial return matrix in this basis, such that it becomes.

Condition (1):.

Translate then condition (1) becomes

(9)

Condition (2):.

Need to find a matrix Q such that We first partition such that it becomes then

Q is a matrix. Condition (2) can then be written in terms of Q and E:

(10)

The final step is then to show that the pseudo equilibrium manifold parameterized by P and Q is locally identified by a diffeomorphism, defined by. The partial derivative exists, moreover, the map is bijective. □

Proposition 3. If is a pseudo FE with production then for every, there exist financial asset prices and investment portfolios such that is a allocational equivalent FE with production.

Proof. Using (Definition 3), let let and let The equivalence of a pseudo equilibrium with production and a financial markets with production then follows from similar arguments as in [16] . □

Long run financial payoffs depend on the technology of the firm, its production capacity installed via financial markets, and on a set of regular prices. Equilibrium does not exist for critical prices. The next step is therefore to introduce rank dependant payoff maps, and to exhibit a class of transverse price, technology, and capacity dependent maps. We will show that equilibria exists for this smooth rank dependent real asset structure, denoted

Definition 5. Define the rank dependent long run payoff maps for The set of reduced rank matrices of order with is denoted and is of order.

Lemma 3. a) For is a submanifold of A of codimension b) for the set is empty, and c) for the set of reduced rank matrices is equivalent to the set of full rank matrices.

Proof. Consider the open set U of matrices of since There exists a matrix such that, and ⁴. □

The lemma states that, for the incomplete income transfer space is rank reduced. The rank dependent endogenized long run asset structure has following properties.

Proposition 4. a) for integers. b) for any and integers c) is generic, since it is dense and open.

Proof. a) The linear map is surjective everywhere in Y. b) This property does not change for any c) Immediate consequence of the transversality theorem for maps. Since each set is residual, their intersection is residual. □

Definition 6. Denote the vector bundle defined by a) a basis and b) orthogonal income transfer space

(11)

We thus have defined a fiber bundle of codimension containing the spot price system and income transfer space consisting of a base vector and fiber We can now state the main result.

Theorem 5. There exists a pseudo FE with production for generic endowments. Moreover, by the relational propositions, a FE with production exists for generic endowments.

Proof. By (Proposition 4) and using (Definition 6) define an evaluation map on, where denote the set of the economy’s total initial endowments, such that the excess demand map

For the Arrow-Debreu agent have

(12)

The evaluation map is a submersion, since is surjective everywhere. for each

(13)

where and The dimension of the preimage is By Thom’s parametric transversality theorem⁵, it follows that the subset is generic since it is open and dense. Equilibria exist. By the equivalence propositions 2 and 3 know that full rank financial markets equilibria with production exist.

For all the preimage of the rank reduced evaluation map has dimension This implies that for generic endowments for there is no reduced rank equilibrium, since for the set of □

4. Conclusion

This paper links the real and the financial sector in a general equilibrium model with incomplete financial markets. Production capacity available to a firm is endogenized and depends on the financial decisions of the firm in period one. At varianve to utility maximizing objective functions of firms, the model developed here considers a long run profit maximization objective function. This rehabilitates the decentralization property of the standard Arrow-Debreu model. It is shown by a parametric transversality theorem that equilibria exists.

NOTES

¹Here, implies differentiability at any order required. The order depends on all transversality arguments employed. M denotes the inputs and n the output elements of the production set, and l = m + n.

²□ denotes the box product. A “s by s” context dependent mathematical operation. For example the s by s inner product.

³See i.e. Dieudonnè [18] for properties of the Grassmann manifold. See Duffie and Shafer for an exposition of the Grassmann manifold in economics [11] .

⁴It is known that constitutes a submanifold complex of. See Hirsch [13] .

⁵See i.e. Hirsch for an exposition of Thom’s parametric transversality theorem [13] . For more on transversality see R. Abraham and J. Robbin (1967), Transversal Mappings and Flows (W. A. Benjamin).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Arrow, K.J. (1953) Le role des valeurs boursières pour la répartition la meilleure des risques. In Economètrie. Fondements et applications de la théorie du risque en économétrie. CNRS, Paris.
[2]	Arrow, K.J. (1964) The Role of Securities in the Optimal Allocation of Risk-Bearing. Review of Economic Studies, 31, 91-96. http://dx.doi.org/10.2307/2296188
[3]	Debreu, G. (1959) Theory of Value. Wiley, New York.
[4]	Drèze, J.H. (1974) Investment under Private Ownership: Optimality, Equilibrium and Stability. in Allocation under uncertainty: Equilibrium and Optimality. In: Drèze, J.H., Ed., Wiley, New York, 129-165. http://dx.doi.org/10.1007/978-1-349-01989-2_9
[5]	Grossman, S. and Hart, O. (1979) A Theory of Competitive Equilibrium in Stock Market Economies. Econometrica, 47, 293-330. http://dx.doi.org/10.2307/1914186
[6]	Duffie, D. and Shafer, W. (1986) Equilibrium and the Role of the Firm in Incomplete Markets. Research Paper 915, Graduate School of Business, Stanford University, Stanford.
[7]	Ekern, S. and Wilson, R. (1974) On the Theory of the Firm in an Economy with Incomplete Markets. Bell Journal of Economics and Management Science, 5, 171-180. http://dx.doi.org/10.2307/3003097
[8]	Geanokopolos, J., Magill, M., Quinzii, M. and Drèze, J. (1990) Generic Inefficiency of Stock Market Equilibrium When Markets Are Incomplete. Journal of Mathematical Economics, 19, 113-151. http://dx.doi.org/10.1016/0304-4068(90)90039-C
[9]	Bottazzi, J. (1995) Existence of Equilibria with Incomplete Markets: The Case of Smooth Returns. Journal of Mathematical Economics, 24, 59-72. http://dx.doi.org/10.1016/0304-4068(94)00672-W
[10]	Debreu, G. (1972) Smooth Preferences. Econometrica, 40, 603-615. http://dx.doi.org/10.2307/1912956
[11]	Duffie, D. and Shafer, W. (1985) Equilibrium in Incomplete Markets I: A Basic Model of Generic Existence. Journal of Mathematical Economics, 14, 285-300. http://dx.doi.org/10.1016/0304-4068(85)90004-7
[12]	Geanokopolos, J. and Shafer, W. (1990) Solving a System of Simultaneous Equations in Economics. Journal of Mathematical Economics, 19, 69-95. http://dx.doi.org/10.1016/0304-4068(90)90036-9
[13]	Hirsch, M. (1972) Differential Topology. Graduate Texts in Mathematics. Springer Verlag, New York.
[14]	Hirsch, M., Magill, M. and Mas-Colell, A. (1990) A Geometric Approach to a Class of Equilibrium Existence Theorems. Journal of Mathematical Economics, 19, 95-106. http://dx.doi.org/10.1016/0304-4068(90)90037-A
[15]	Husseini, S.Y., Lasry, J.M. and Magill, M. (1990) Existence of Equilibrium with Incomplete Markets. Journal of Mathematical Economics, 19, 39-67. http://dx.doi.org/10.1016/0304-4068(90)90035-8
[16]	Magill, M. and Shafer, W. (1990) Incomplete Markets. Chapter 30. In Hildebrand, W. and Sonnenschein, H., Eds., Handbook of Mathematical Economics, Vol. IV, 1523-1614.
[17]	Cass, D. (1984) Competitive Equilibria with Incomplete Financial Markets. CARESS Working Paper #84-09. University of Pennsylvania. (2006) in Journal of Mathematical Economics.
[18]	Dieudonnè, J. (1972) Elèments d’analyse. Gauthier-Villars, Paris.