A Theory of Ratio Selection—Lattice Model for Obligate Mutualism ()
Received 26 February 2016; accepted 10 May 2016; published 13 May 2016
1. Introduction
In recent years, the concern for mutualism is growing, since almost all species have mutualistic relationship with other species [1] - [4] . Microbial species influence on the abundances and ecological functions of related species [5] [6] . Many bacterial species coexist in a syntrophic association; that is, one species lives off the products of another species. Here, we pay attention to obligate mutualism between a pair of species; one species cannot survive without the other. The systems of obligate mutualism usually have some mechanism to avoid a sudden increase (or decrease) of one species [1] . We discuss the reason why such a mechanism is necessary.
The relationship of obligate mutualism has the similar behaviour as the male-female relationship [7] - [9] : female (or male) cannot get offspring without the partner. The sex ratio of many animals is nearly one-to-one. Fisher (1930) first explained the reason why the 1:1 sex ratio is optimal [10] . Later his argument was recognized as in the framework of evolutionarily stable strategy (ESS) [11] [12] . However, Fisher’s theory has some problems [13] [14] . For example, his theory may conflict with real data. In most animals, the sex ratio (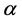
) at birth is slightly biased (
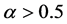) [15] . Consider a large population (resident) which is slightly biased (say
). According to Fisher’s theory, the resident is easily beaten by all mutants which satisfy
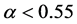; in particular, the mutant of asexual reproduction (
) is optimal [16] .
It is known that ESS is the most powerful tool to obtain the optimal strategy which beats the other strategies [11] . To win such competitions may be one of most important driving forces in evolution, but it is not a necessary condition for evolution. For instance, the most sustainable strategy is advantageous for evolution [16] - [18] . Yoshimura et al. have explained the evolutionary origins of periodical cicadas in North America not by ESS but by sustainability [17] [18] . If the competition is dominant, real cicadas (13-and 17-year cycles) might be beaten by the other phenotypes with shorter cycles. The sustainability also explains the fact that the life span of species is not so long [19] . Similarly, Tainaka et al. (2006) have explained the evolution of 1:1 sex ratio on the basis of sustainability [8] . In the present paper, we extend this idea to obligate mutualism.
Lattice models have been applied to ecological problems, where simulations have been carried out by two methods: local and global interactions [20] [21] . In the former, interactions occur between neighboring sites, whereas in the latter they occur between any pair of lattice sites. The simulation of global interaction is often called “lattice gas model” [9] [22] [23] ; individuals contact like the collision of gas molecules. In most cases, the dynamics of global interaction can be represented by mean-field theory. However, for the local interaction, there are usually no theories; simulations are thus necessary to obtain various results.
The most famous model of population dynamics in ecology is Lotka-Volterra equations (LVEs) [24] [25] . However, they have a flaw, when we apply them to mutualism [4] [25] . For example, the population sizes of both species may increase infinitely (“divergence problem”) [25] . Moreover, LVEs never predict Allee effect for obligate mutualism [7] . Recently, Iwata et al. [9] introduced a simple population model for mutualism, applying the lattice gas model. They assume that all interactions occur between any pair of cells. In their model, the divergence has never occurred, and Allee effect has been derived in a simple form. The present work is the local-interaction version of Iwata’s model. Especially, we explore equilibrium densities to know the sustainability of populations.
In the next section, we explain our model and method of both local and global interactions. In Section 3, the prediction by mean-field theory is reported. We briefly describe the results obtained by Iwata et al. [9] , and we add new results, such as equilibrium densities. Section 4 is devoted to report simulation results. In the case of local interaction, the dynamics is similar to those for global interaction, such as Allee effect. However, there is a large difference between local and global interactions. In the former case, the sustainable range in parameter space is very narrow, compared to global interaction. Namely, the proportion (ratio) between both species is strongly restricted for their survival. In the final section, we present an idea of “ratio selection” which is an extension of the sex-ratio selection [12] - [15] .
2. Model and Methods
2.1. Model
Consider a system consisting of two mutualistic species X and Y (Figure 1). Each lattice site is labeled by X, Y or O, where O means the empty site. The empty cell is introduced to prohibit the divergence of population sizes [9] . The reactions are defined by
(1a)
![]()
Figure 1. Lattice model for obligate mutualism. The cell X (Y) indicates the occupation site (individual) of species X (Y), and O is empty. The empty cell is introduced to avoid the divergence of population sizes [13] .
(1b)
(1c)
(1d)
The reactions (1a) and (1c) respectively denote the birth and death processes of species X, and 
(
) denotes the reproduction (mortality) rate of species X. Similarly, the reactions (1b) and (1d) mean the birth and death processes of species Y, respectively.
2.2. Method
Simulations of lattice model are usually carried out by either local or global interaction [8] [20] . First, we explain the simulation procedure of local interaction. Reaction processes are performed in the following steps:
1) Initially, we distribute X, Y on a square lattice. Each cell is one of three sites: X, Y, and O (see Figure 1).
2) To update, we choose a target site randomly.
a) Reaction (1c) or (1d): If the target cell is X (or Y), then it becomes O by the rate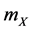 
(or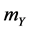
).
b) Reaction (1a) or (1b): If the target site is O, we choose another cell from the neighboring 8 sites (Moore neighborhood) around the target cell. When the second site is X (or Y), then the target cell become X (or Y) by the rate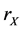 
(or![]()
).
3) We repeat step 2) by ![]()
times, where ![]()
is the lattice size and ![]()
is the total number of sites (![]()
). This step is a unit time called the Monte Carlo step.
4) We further continue the updates, until the system reaches stationary state.
The reproduction rates ![]()
and ![]()
for local interaction are assumed that
![]()
,![]()
(2)
where we call ![]()
(![]()
) the birth rate of species X (Y), and ![]()
(![]()
) the neighboring density of species X (Y). For instance, if there are five X cells in the Moore neighborhood, we put![]()
.
Next, we explain the method of global interaction (lattice gas model). Almost all procedures are the same as local interaction. However, in the global simulations, the birth process [reaction (1a) or (1b)] occurs between any pair of lattice sites. In mean-field limit, the reproduction rates are replaced as follows:
![]()
,![]()
(3)
where ![]()
(![]()
) is the overall density of species X (Y).
3. Prediction of Global Interaction
If the reaction (1a) occurs between any pair of lattice sites, and if the lattice size ![]()
is sufficiently large, then the mean-field theory holds:
![]()
(4a)
![]()
(4b)
where the factor ![]()
in the right hand sides denotes the density of empty cell. The first and second terms in Equation (4) come from birth and death processes, respectively. Inserting Equations (3) into (4), we have
![]()
(5a)
![]()
(5b)
Note that this equation is almost the same as in the male-female system [7] [8] . Iwata et al. [9] proved that the Equation (5) led to one of two phases: extinction or Allee-effect phase (Figure 2). In the former case, both species always go extinct. The latter is called the survival/extinction (S/E) phase, because this phase has two stable equilibriums which means survival and extinction. The condition for the Allee-effect phase has been represented by
![]()
(6)
In summary, two conditions are necessary for survival; one is the relation (6), and the other is that initial densities of two species are higher than the separatrix which is schematically shown in Figure 2(b).
We explicitly obtain equilibrium density in stable state, when
![]()
(7)
![]()
(a) (b)
Figure 2. Schematic illustration of population dynamics. (a) extinction phase, and (b) Allee effect phase [13] .
From Equations (5) and (7), we get
![]()
(8)
where
![]()
(9)
From Equation (8), we can find the following relation: ![]()
for![]()
. This means that the equilibrium density satisfies
![]()
(10)
Inserting Equations (7) and (10) into (5), we have
![]()
(11)
where![]()
, ![]()
and
![]()
(12)
Equation (11) denotes a typical Allee-effect equation [7] . According to the sign of D, the dynamics is classified into two phases: extinction phase for ![]()
and Allee-effect phase for![]()
. So long as initial densities of both male and female are high enough, the steady-state densities in survival phase is given by
![]()
,![]()
. (13a)
![]()
(13b)
It is therefore found in the mean-field limit that 1) the maximum value of total density (![]()
) is achieved at![]()
, 2) a positive stable equilibrium (Allee-effect phase) exists, when ![]()
or
![]()
(14)
This inequality is the same as equation (6) under the condition of![]()
.
4. Simulation Results
We report simulation results of individual-based (lattice) model. In the case of global interaction, the mean-field theory [Equation (5)] predicts that the dynamics has two phases. One is an extinction phase: both species always go extinct. The other is Allee-effect phase. A typical example of the latter phase is shown in Figure 3 (![]()
), where (1) represents simulation result and (2) is the prediction by mean-field theory. All orbits asymptotically reach one of two stable equilibria (filled circles). Both equilibria locate on the dotted line represented by Equation (10). The densities of both species at survival equilibrium (right filled circle) are expressed by Equation (13a). Unless both densities are considerably high, both species goes extinct. The red curve denotes the separatrix which determines whether the final equilibrium is survival or extinction state. The unstable equilibrium (open circle) locates on the separatrix. We confirm the results of global simulation are well predicted by mean-field theory [Equation (5)].
In the case of local interaction, the dynamics are similar to the predictions of lattice gas theory. For instance, the Allee effect can be observed: unless both densities of species are considerably high, the population goes extinct. However, in the case of local interaction, simulation results exhibit a distinct difference from those of global interaction. In Figure 4, typical spatial distributions in stationary state are displayed (![]()
), where (1) and (2) are the patterns of global simulation, and (3) and (4) are those of local simulation. The value of ![]()
is optimal at![]()
; the total population size takes the maximum value at ![]()
[see Figure 4(a) and Figure 4(c)]. In contrast, both Figure 4(b) and Figure 4(d) display at![]()
. It is found from Figure 4(d) that the total population size largely decreases, when the value of ![]()
slightly deviates from the optimality.
In Figure 5, the steady-state densities are plotted against![]()
, where we assume![]()
. In the case of global simulation, the survival range of ![]()
is very wide [see Figure 5(a)]. Both species can survive for any
ratio of densities. However, it is necessary for the sustainability in local interaction that the value of ![]()
should be very close to 0.5 [see Figure 5(b)]. In other word, both species must have 1:1 ratio for the sustainability.
When![]()
, the sustainable range becomes biased. Figure 6 is the same figure as Figure 5, but the mortality rate of X is much higher than that of Y (![]()
). In global simulation, almost all ratios between species X and Y are sustainable. However, in local simulation, both species can coexist near ![]()
where the total density takes the maximum value. The ratio (![]()
) of both birth rates is largely X-biased; namely, the birth rate (![]()
) of species X must be higher than ![]()
for the survival of both species. The survival condition is strongly restricted in local simulation.
5. Discussions
We have developed a lattice population of obligate mutualism. Local interaction strongly effects on the populations dynamics. The survival condition is extremely limited for local simulation. When both species have the same mortality rate (![]()
), it is necessary for the sustainability in local interaction that both species must have 1:1 ratio (see Figure 5). When the mortality rate of species X is larger than that of Y (![]()
), the birth rate of X must be larger than that of Y (see Figure 6). In the case of local interaction, a severe condition is required. Individuals of both species must live together in close proximity. On the basis of these results, we present a theory of “ratio selection” for obligate mutualism. When two species interact locally (long-range interaction is prohibited), both species require a specific (proper) ratio. The proper ratio may be determined by various factors, such as mutual body sizes, mutual shapes and obligate requirements of both species.
The ratio selection is a generalization of sex-ratio selection. In fact, our model is also applicable to the male- female system. Equation (5) is almost the same as obtained in male-female system [7] [8] , where X (Y) corresponds to male (female) and ![]()
means the sex ratio at birth. Fisher first explained the evolution of 1:1 sex ratio [10] . However, as described before, his theory (ESS) cannot explain real data of male-biased sex ratio [16] [26] [27] . On the other hand, the present work well explains the male-biased sex ratio (![]()
). As shown in Figure 6(b), the biased sex ratio is explained by the fact that the mortality rate of male is slightly higher than that of female (![]()
). Since males rapidly die than females, the inequality ![]()
is necessary to keep mutual encounter (close proximity). According to ESS, the strategy of ![]()
is optimal. However, this strategy cannot survive, because its steady-state density is zero [see Figure 6(b)].
Many empirical data suggest the ratio selection; two-species systems of obligate mutualism usually have some mechanism to avoid an abrupt increase of one species [1] . 1) Coral and algae: the ratio between cell number in stomach (“gastrodermis”) of coral and zooxanthellae number is just 1:1 [28] . When the density of algae is too high, the excess algae are excluded from coral. 2) Chlorella and Paramecium: the number of Chlorella (Chlorella) inside each body of Paramecium (Paramecium bursaria) is about 400 individuals [29] . 3) Yucca and
yucca moth: too many yucca moths become harmful for yucca plant [30] . 4) Chloroplast and mitochondria: the number of these organelles in a host cell is not so arbitrary [31] . The ratio selection comes from the requirement that all individuals of one species need a high local density of the other species. We consider such requirement evolutionarily leads to endosymbionts from free-living ancestors [32] . This is because endosymbiosis is more stable than free living to keep their proper ratio. Similarly, the ratio selection may be a driving force for the evolution from endosymbionts to organelles [33] [34] .
Acknowledgements
The authors sincerely thank to professors Jin Yoshimura for valuable comments. They also thank to Mr. Keiji Amemiya for the help of simulations.