Received 29 January 2016; accepted 9 May 2016; published 12 May 2016

1. Introduction
It is well-known that between such spheres of technical cybernetics as location, positioning and remote sensing, the firm interrelation does exist. The information theory based grounding of such an interrelation firstly is described in the work [1] .
The properties of thermal location are that the pixel type structure of images used for location purposes by scanning airborne radiometers leads to inevitable errors of integrated assessment of signal. Upon thermal scanning of surface of researched object, if the latter contains two different surface materials, all radiation emitted from these materials located within one pixel will be averaged as a single pixel signal depending on wavelength of sensor’s operational channel.
According to [2] , utilization of integral of Planks function for different channels of airborne radiometer makes it possible to compute following parameters:
1) Radiation temperature of one of two temperature fields on sub pixel level of resolution;
2) Share of each component of temperature field within pixel (that is temperatures of the object and background).
If assume, that effect of atmosphere is lacking, the upward radiation at the input of airborne scanning radiometer will be determined as [1]
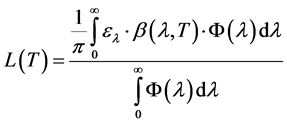 (1)
(1)
where: ―emissivity at the wavelength λ;
―emissivity at the wavelength λ;
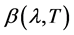 ―Plank’s function, W∙m−3;
―Plank’s function, W∙m−3;
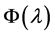 ―sensor’s spectral instrument function.
―sensor’s spectral instrument function.
The Planks functions of black body with temperature T at the wavelength λ is determined as
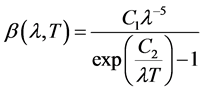 (2)
(2)
where: С1―the first constant of Plank, equals to 3.741832 × 10−16 W∙m2;
С2―the second constant of Plank, equals to 1.438786 × 10−2 m∙k;
Т―temperature, K;
λ―wavelength, μm.
The property of the Planks function is that if in the fixed temperature T1, the signal at the wavelength λ1 surpasses the signal at the wavelength λ2 in sufficiently higher temperature T2, the contrary case does occur.
This property of the Plank’s function is illustrated in Figure 1, where the output signals of 3-rd and 4-th channels of AVHRR radiometer installed on the board NOAA-6 are shown. As it seen from shown graphics upon temperature above 460 K, the signal of 4-th channel (102 - 116 μm) surpasses the one of 3-rd channel (35 - 40 μm).
The above said property is the bases of the Dozier’s method [2] , according which the total radiation emitted from non-homogenous, two-parts structured pixel at the surface of researched site upon lacking of atmospheric effect can be computed as
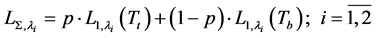 (3)
(3)
where: p―weight coefficient; 0 < p < 1;
![]()
Figure 1. Dependence of signals of 3-rd and 4-th channels from temperature in spectroradiometer AVHRR of satellite NOAA-6.
Tt―objects temperature;
λ1, λ2―wavelengths used for measurements.
According to the Dozier’s method upon carrying out measurements at the wavelengths λ1 and λ2, if the value of Tb is known, the amount of p and Tt can be calculated using the system of Equation (3). It should be noted that to remove any possible dynamic errors, all measurements upon realization of this method should be carried out synchronously. This method makes it possible to carry out the sub pixel remote identification of hidden and remote objects.
2. Further Development of Doziers Bispectral Method and Suggested Biparametric Generalization
The Dozier’s method further was developed and modernized in works [3] - [6] .
Let us consider in brief the modernized Dozier’s method described in [6] . In this modification the limitation imposed in [2] is characterizing the consideration of only ground component of radiation. In the work [6] the general case of remote assessment of parameters of heated remote sub pixel object is considered taking into account the effect of atmosphere. The Equation (3) in this case should be written as
 (4)
(4)
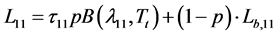 (5)
(5)
where: Lb,4 and Lb,11―atmospheric radiations at the wavelength 4 μm and 11 μm;
τ4 and τ11―atmospheric transfer at the pertinent wavelengths.
Operationally, Lb,4 should be determined by averaging the radiation of neighbor pixels, assuming that these pixels are identical on temperature. Solution of Equations (4), (5) relative p an Ti is carried out as following. From Equations (4) and (5) we get
 (6)
(6)
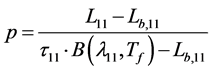 (7)
(7)
Equalling (6) and (7) we get
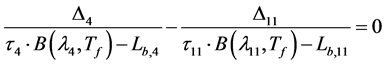 (8)
(8)
where: ;
;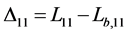 .
.
If assume, that the radiation parameters of background are known, then obviously both components of the left side of equation (8) upon Tf ® ∞ asymptotically go near to zero. The solution of the task is gradual increase of Tf till the first component at the left side of (8) would approach zero with acceptable accuracy. Thus, the above said method named as Dozier method make it possible to calculate parameters p and Tt of sub pixel heated object carrying out radiometric measurements at the wavelength λ1 = 4 μm; λ2 = 11 μm. The suggested three- measured interpretation of the Dozier method is illustrated in Figure 2. The Figure 2 illustrate scheme of radiometric measurements at the wavelengths λ1 and λ2 at the moment to carried out for identification of sub pixel object with temperature Tto. As it is seen from three-measured diagram the line AB determines the graphical interpretation of carried out bispectral measurements.
The suggested generalization of Dozier’s bispectral method named as biparametric method is applicable for static remote objects. We assume that in the time interval 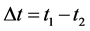 the temperature of static remove object changes from Tt1 as far as Tt2 (Figure 3). The measurements are carried out at the single wavelength. The characteristics of the searched object is that the function
the temperature of static remove object changes from Tt1 as far as Tt2 (Figure 3). The measurements are carried out at the single wavelength. The characteristics of the searched object is that the function
![]() where: t―time of day, is approximately known.
where: t―time of day, is approximately known.
![]()
Figure 2. Three-measured interpretation of Dozier’s method applicable for remote objects with unchanged temperature.
![]()
Figure 3. Three-measured interpretation of suggested biparametric method applicable for remote objects with changing temperature.
In the suggested biparametric method the measurements are carried out at the moments t1 and t2. It is assumed that the object temperature reaches quantity T(t1) and T(t2) at these moments. The Equations (4) and (5) in the suggested biparametric method should be written as
![]() (9)
(9)
![]() (10)
(10)
From the Equation (9) we find
![]() (11)
(11)
From Equation (10) we get
![]() (12)
(12)
From both the Equation (11) and (12) we get
![]() (13)
(13)
If according the initial condition ![]() are known, the parameter
are known, the parameter ![]() can be calculated using Equation (13). Then using one of Equations (6) or (7) the parameter p can be calculated. In order to determine distance as far as an object the following assumption is used. On the bases of operational data of scanning IR radiometer the square area of one pixel can be calculated in dependence of distance between object and radiometer
can be calculated using Equation (13). Then using one of Equations (6) or (7) the parameter p can be calculated. In order to determine distance as far as an object the following assumption is used. On the bases of operational data of scanning IR radiometer the square area of one pixel can be calculated in dependence of distance between object and radiometer
![]() (14)
(14)
where: Spix―square area of one pixel on the surface of object; l1―distance between radiometer and object.
If
![]() (15)
(15)
where: Sob―square area of searched object.
In view of (14) and (15) we get
![]() (16)
(16)
Having calculated l1 on the bases of Equation (16) we come to conclusion that the searched object is situated at the distance l1 from the radiometer. Obviously that in order to locate the object all above procedures should be repeated from another base point. Suppose that the second point is situated in distance l2 from the radiometer. To locate the object it is quite sufficient to draw circles with radius l1 and l2 from these bases points and the crossing point of these circles will determine the point of location of object.
3. Conclusion
Thus it is shown that the suggested generalization of the Dozier’s method named as biparametric sub pixel method of thermal location makes it possible to carry out such a location of static objects from two basis points using serial single wavelengths measurements of radiation emitted by the sub pixel object. Such a modification of Dozier’s method shows the universal character of two-parametric concept of measurements. Utilization of two wavelengths in known Dozier’s method and two serial time moments in suggested modification of the method prove the big potential of two-parametric concept of remote sub-pixel measurements.