G-CPT Symmetry of Quantum Emergence and Submergence—An Information Conservational Multiagent Cellular Automata Unification of CPT Symmetry and CP Violation for Equilibrium-Based Many-World Causal Analysis of Quantum Coherence and Decoherence ()
Received 3 November 2015; accepted 4 May 2016; published 9 May 2016

1. Introduction
1.1. CPT Symmetry
Charge-Parity-Time (CPT) symmetry is widely regarded as a fundamental property of physical laws that govern the evolution of our universe. It is a common belief that a CPT transformation turns our universe into its “mirror image” and vice versa. It has the implication that a “mirror-image” of our universe―with all objects having their positions reflected by an arbitrary plane (corresponding to a parity inversion), all momenta reversed (corresponding to a time inversion) and with all matter replaced by antimatter (corresponding to a charge inversion)―would evolve under exactly our physical laws. In order to preserve CPT symmetry, every violation of the combined symmetry of two of its components (such as CP) must have a corresponding violation in the third component (such as T); in fact, mathematically, these are the same thing. Thus, violations in T symmetry are often referred to as CP-violations. CP-violation is the violation of the combination of C-symmetry (charge conjugation symmetry) and P-symmetry (parity symmetry). CP-symmetry states that the laws of physics should be the same if a particle is interchanged with its antiparticle (C symmetry) and when its spatial coordinates are inverted (“mirror” or P symmetry). The discovery of parity non-conservation or P-violation [1] [2] in weak interaction resulted in the Nobel Prize in Physics in 1957 for its discoverers Tsung-Dao Lee and Chen-Ning Yang. The discovery of CP-violation [3] in the decays of neutral kaons resulted in the Nobel Prize in Physics in 1980 for its discoverers James Cronin and Val Fitch. CP-violation under CPT symmetry plays an important role both in the attempts of cosmology to explain the dominance of matter over antimatter in the present universe and in the study of weak interactions in particle physics.
It can be argued that, without a formal geometrical and logical basis for equilibrium-based bipolar coexistence, CPT symmetry as a truth-based model is an incomplete or even flawed theory. For instance, we know that once antimatter and matter existed in near perfect unitary counterbalance but antimatter vanished without a trace on a cosmic scale. This remains one of the greatest mysteries of the universe. On the other hand, newly discovered particle-antiparticle oscillation [4] and neutrino oscillation [5] show clear evidence of Nature’s bipolar coexistence in a dynamic equilibrium, but the bipolar coexistence is missing from CPT symmetry and the role of CP-violation has not been made clear in the theories of quantum coherence and decoherence or collapse. Thus, many questions remain unanswered by CPT symmetry, some of them are posted as the first set of key questions of this paper.
Questions of Group 1. Why “mirror-image”? Isn’t our universe in a dynamic equilibrium of bipolar coexistence of particle-antiparticles and negative-positive energies? Is there a unification of energy and information? What is the logic of CPT symmetry? What is the geometry of CPT symmetry? What is the cause of CPT symmetry? What is the role of CP-violation in quantum coherence and decoherence or collapse? Is there a logical unification of CPT symmetry and CP violation? Without bipolar dynamic equilibrium can any truth-based model be complete?
1.2. Emergence and Submergence
In a classical world, emergence is the process of coming into view or becoming exposed after being concealed. Generally speaking, it is the process of coming into being important or prominent. While natural and social emergence is observed everywhere in the classical world, emergence at the quantum level remains a mystery undefined logically and mathematically. Up to this day, we do not have a generally accepted view on how quantum superposition and entanglement emerges, how matter and antimatter emerges, and how spacetime emerges after the Big Bang. Even worse, after decades intensive research, we still don’t know how some important quantum phenomena can disappear. Besides, the supposedly spacetime disappearance into a black hole, as a bottleneck of quantum mechanics and quantum computing, quantum decoherence and collapse theories associated with measurements, has been without a major theoretical breakthrough for decades. If quantum coherence is an emergence, could quantum decoherence or collapse be submergence? If so, how can we define quantum emergence and submergence as opposite processes in logical and mathematical terms?
The difficulty with the collapse approach is that, given an initial state with a certain symmetry, one cannot end up with a state that fails to have the symmetry in question. The problem is that Shrödingier’s equation is fully deterministic and the only place where determinism is lost in the context of quantum theory is at the point where one addresses the connection with the measurements. Thus, researchers of dynamical collapse theories seek to modify quantum theory by assuming a fundamental departure from Shrödingier’s deterministic wave function. Roger Penrose has been a strong advocate for such a departure [6] who is recently joint by Steven Weinberg [7] in advocating the incorporation of gravitation into the picture of relativistic quantum field theory. Although this suggestion is sometimes marked as a fancy theory, it cannot be easily dismissed. Unlike electric forces which can be attractive or repulsive, nothing “cancels” gravity because it is only attractive, unless a symmetrical gravitational source is created. All objects having mass are subject to the gravitational force. Therefore, only gravitation matters on the large scale structure of the universe.
Different from quantum collapse, quantum decoherence in quantum mechanics is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition while a total superposition of the global or universal wave function is assumed remain intact (and remains coherent at the global level). Since quantum computers are expected to rely heavily on the undisturbed evolution of quantum coherence, decoherence becomes a bottleneck for the practical realization of quantum computers which require that coherent states be preserved and that decoherence be managed, in order to actually perform quantum computation. Research on decoherence has gained momentum in recent decades since it is proposed in 1970 [8] - [10] . Zurek’s work followed the many worlds interpretation by Everett and Wheeler [11] - [13] , the many worlds in this theory has not reached a unifying geometrical and logical basis. The classical and quantum worlds distinction is, however, quite attractive for modeling quantum decoherence associated with the “measurement problem.”
While no major theoretical breakthrough has been reported in this research area, in July 2011, researchers from University of British Columbia, Canada, and University of California, Santa Barbara, were able to reduce environmental decoherence rate “to levels far below the threshold necessary for quantum information process- ing” by applying high magnetic fields in their experiment [14] . The physical breakthrough shows that a causal interpretation of decoherence is possible. But the cause-effect relation remains largely a logical mystery and the cellular nature of the global coherence and local decoherence has never been made clear. Now we post the 2nd set of key questions:
Question of Group 2. Can quantum emergence and submergence be a unifying theory of coherence and decoherence? Can a quantum cellular automaton be bipolar equilibrium-based? Can the cause of coherence and decoherence be geometrically and logically revealed? Can CP-violation be the cause?
1.3. Coherence and Decoherence of Quantum Cellular Automata
While it seems that there is no good option capable of addressing the issue at hand within the existing range of interpretational approaches to quantum theory, new interpretations of quantum mechanics have been reported. A cellular automaton interpretation (CAI) is proposed and strongly advocated by Gerard ‘t Hooft [15] . He points out that “Einstein may still have been right, when he objected against the conclusions drawn by Bohr and Heisenberg. It may well be that, at its most basic level, there is no randomness in nature, no fundamentally statistical aspect to the laws of evolution. Everything, up to the most minute detail, is controlled by invariable laws. Every significant event in our universe takes place for a reason, it was caused by the action of physical law, not just by chance.” ‘t Hooft stated: “We set up a systematic study of the Cellular Automaton Interpretation of quantum mechanics. We hope to inspire more physicists to do so, to consider seriously the possibility that quantum mechanics as we know it is not a fundamental, mysterious, impenetrable feature of our physical world, but rather an instrument to statistically describe a world where the physical laws, at their most basic roots, are not quantum mechanical at all.” However, ‘t Hooft conceded: “Sure, we do not know how to formulate the most basic laws at present, but we are collecting indications that a classical world underlying quantum mechanics does exist.” He stated: “Not all issues will be resolved, and the suspicion is aired concerning the source of our difficulties: quantum gravitational effects may be of crucial importance, while it is exactly these effects that are still not understood as well as is needed here.”
Notably, ‘t Hooft avoided the quantum coherence and decoherence problem in his CAI interpretation of quantum mechanics. He stated: “Some authors do suspect that gravity is a new elementary source of ‘quantum decoherence’, but such phrases are hardly convincing. …Anyway, decoherence [9] is a vague concept that we completely avoid here.”
While the CAI interpretation by ‘t Hooft can be deemed a truth-based realist approach to quantum mechanics, an equilibrium-based bipolar quantum cellular automata (BQCA) theory is presented in [16] . A distinguishing property of BQCA is its unique philosophical, geometrical and logical basis of YinYang bipolar relativity backed with bipolar quantum geometry (BQG), bipolar dynamic logic (BDL) and bipolar quantum linear algebra (BQLA) that leads to an equilibrium-based interpretation of quantum mechanics and a number of unifications [16] - [26] . Different from particle-wave complementarity and spacetime relativity, YinYang bipolar relativity claims that bipolar quantum interaction and complementarity is the source of causality for the formation and mutation of reality, any other complementarity or relativity is less fundamental. While other background independent geometries [cf. [27] ] so far came short of providing a causal logic, it is shown that causality is logically definable with BDL and BQLA within the background independent geometry BQG. Now we post the 3rd set of key questions:
Questions of Group 3. Could a cellular automaton interpretation of quantum mechanics provide a fundamental departure from the established theories and observations? How does the new interpretation relate quantum superposition and entanglement to agents in quantum and classical worlds? Can quantum emergence and submergence unify quantum coherence, decoherence and collapse theories under a generalized theory of CPT symmetry? Can local BQCAs form a globally coherent BQCA? Can the nature of coherence and decoherence be revealed by multiagent BQCA emergence and submergence?
1.4. Background Independence
Background independence is a desirable property in the quest for quantum gravity. Lee Smolin is best known for advocating background independence in his quest for loop quantum gravity [27] . But so far no formal logical system has been reported for background independent geometrical reasoning with definable causality from any of the three major approaches to quantum gravity, namely, string theory, loop quantum gravity and M-theory. BDL seems to be the only logical system of its kind which is used as a basis for YinYang bipolar quantum gravity [16] [17] .
The crux of the problem is that there is no precise definition for background independence. We need a minimum set of necessary and sufficient conditions for complete background independence. Without such a set of conditions, a unique logical foundation for quantum gravity cannot be developed. For instance, until this day, a popular definition of a background independent geometry requires the unnecessary condition of being coordinate-free but does not require the imperative condition of supporting both reductionism and emergence. This definition failed to realize that some coordinate can be completely background independent. Without any such coordinate, it would be impossible to have background independent logical reasoning on quantum emergence and submergence. The unnecessary and insufficient conditions have inhibited the development of a truly background independent geometry and a new formal logical foundation for quantum gravity. As a result, the quest for quantum gravity has so far failed to find a definitive battleground and quantum superposition and entanglement still find no formal logical definition in Hilbert space. Now we post the 4th set of key questions:
Questions of Group 4. What is complete background independence? Could quantum superposition and entanglement be logically characterized as background independent quantum emergence? Could quantum decoherence and dynamic collapse be characterized as quantum submergence? Could quantum decoherence and collapse be fundamentally CP-violation under a generalized CPT symmetry? Can a background independent geometry have a coordinate? Can a quantum world be unified with a classical world within a background independent geometry?
1.5. Approach and Organization of This Work
In a search for answers to the four groups of questions, this work presents G-CPT symmetry―a fundamentally different interpretation of quantum mechanics (Note: The notion “G-CPT symmetry” is first coined in [21] ). It is argued that particle-wave complementarity is inadequate; an analytical paradigm is needed for addressing the problems identified. Such a new paradigm must reproduce the observations of quantum mechanics but goes beyond the impasse with a new philosophical, geometrical and logical foundation of physics as envisaged by Einstein in last century.
This work is organized in six sections. Section 2 presents a background review and analysis of the basic development of the theory with scientific support. Section 3 presents G-CPT symmetry as an equilibrium-based quantum cellular generalization of CPT symmetry―a unifying paradigm of quantum emergence and submergence for causal analysis of quantum coherence and decoherence or collapse. Section 4 presents a many-world model of quantum emergence and submergence. Section 6 presents a discussion and makes a number of predictions based on the theory. Section 5 draws a few conclusions.
2. Background
2.1. From Wave-Particle Duality to YinYang Bipolar Relativity
Niels Bohr was the first to bring YinYang into quantum theory for his wave-particle duality principle. When Bohr was awarded the Order of the Elephant by the Danish government, he designed his own coat of arms (Figure 1(a)) which featured in the center a YinYang logo and the Latin motto contrariasuntcomplementa or “opposites are complementary” in English.
It is observed, however, that particle and wave are not direct opposites. While Bohr recognized wave-particle complementarity, he stopped short of identifying the essence of YinYang bipolar coexistence and bipolar complementarity (Figure 1(b)).
Theoretically, if bipolar dynamic equilibrium of negative-positive energies and/or input-output information is the most fundamental form of equilibrium, any multidimensional model in spacetime geometry is less fundamental. A YinYang bipolar complementarity principle is, therefore, imperative for a bipolar equilibrium-based logical interpretation of the quantum world.
YinYang bipolar complementarity principle claims that action-reaction, particle-antiparticle, input-output, negative-positive energies, or the Yin and the Yang of Nature in general constitute the direct opposites (Figure 1(b)), form the most fundamental complementarity, and provide the source of causality for being and changes [16] . On the other hand, without bipolarity, any complementarity is less fundamental due to the missing “opposites” (Figure 1(c) & Figure 1(d)) (Note: Newtonian action and reaction are equal opposites that are extended to include non-equal opposites to account for modern discoveries such as CP violation or input-output imbalance).
According to the bipolar complementarity principle, man-woman, space-time, particle-wave, truth-falsity, mind-matter, and imaginary-real complementarities are not exactly bipolar opposites, not bipolar interactive and, thus, less fundamental. For instance, while particle-wave and space-time do not form symmetries and do not interact with each other as bipolar opposites, they can be posited the result of particle-antiparticle bipolar interaction. It is suggested that this could be the reason why Bohr asserted that a causal description of a quantum
![]()
Figure 1. (a) Bohr’s coat of Arms (creative commons file by GJo, 3/8/2010, File: royal coat of Arms of Denmark.svg + File: yinyang.svg); (b) Fundamental bipolar complementarity; (c)-(d) Non-fundamental com- plementarities.
process cannot be attained and quantum mechanics has to content itself with wave-particle complementary descriptions [28] . It can be posited that, due to this limitation, both particle-wave complementarity and space-time relativity theories so far have not evolved to a general purpose logical system for quantum mechanics or quantum gravity and, without such a logical system, the nature of quantum decoherence or collapse has remained a logical mystery.
2.2. Quantum Superposition and Bra-Ket Notation
Quantum superposition plays a key role in quantum coherence. In his textbook, Paul Dirac [29] introduced the concepts of quantum superposition and indeterminacy using polarized photons in a 3-polarizer experiment (Figures 2(a)-(d) and Equation (1)). As Dirac stated ( [29] : p. 11): “There remains an overall criticism that one may make to the whole scheme, namely, that in departing from the determinacy of the classical theory a great complication is introduced into the description of Nature, which is a highly undesirable feature. This complication is undeniable, but it is offset by a great simplification, provided by the general principle of superposition of states, which we shall now go on to consider.” Albert Einstein commented on Dirac’s experiment [30] : “Dirac, to whom, in my opinion, we owe the most perfect exposition, logically, of this theory, rightly points out that it would probably be difficult, for example, to give a theoretical description of a photon such as would give enough information to enable one to decide whether it will pass a polarizer placed (obliquely) in its way or not.”
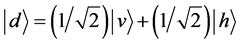 (1)
(1)
Despite the theoretical significance, Dirac’s examples suggest a very simple and inexpensive experiment to demonstrate quantum superposition of polarized photons. Such an experiment is usually performed in high school physics labs. The experiment tells us:
1) Light gets through polarizers (filters) A and B if both are aligned vertically (or horizontally) (Figure 2(a));
2) If polarizer A remains in vertical polarization and polarizer B is rotated 90˚ to horizontal polarization, no light gets through (Figure 2(b));
3) Light partially gets through the intersection of polarizer C with polarizer A and polarizer B if C is turned along the diagonal 45˚ and slipped between A (in the rear) and B (in front) (Figure 2(c)).
According to Dirac, with complex number coefficients that represent “probability amplitudes”, the diagonally polarized photon can be represented as a superposition of vertical v and horizontal h states with bra-ket notation in Hilbert space (Figure 2(d), Equation (1)). Local quantum superposition led to the non-local phenomenon of quantum entanglement. Quantum mechanics has never provided a logical definition for quantum superposition and entanglement. No logical exposition of the 3-polarizer experiment was reported in quantum mechanics.
Einstein and Schrödinger later attacked the idea of superposition by arguing that it would apply to macroscopic objects like a cat being alive and dead. This quantum phenomenon has been referred to as Schrödinger’s Cat paradox. On the other hand, the quantum mechanical interpretation of entanglement is questioned by the EPR paper [31] . Einstein famously called quantum entanglement “spooky action at a distance” and refused to accept quantum mechanics as a complete theory.
![]()
Figure 2. Dirac three polarizer experiment and quantum superposition: (a) Two vertical (or horizontal) polarizers; (b) A vertical polarizer and a horizontal one; (c) A diagonal polarizer inserted between a vertical and a horizontal polarizer; (d) Quantum superposition (http://creativecommons.org/licenses/by/3.0/).
2.3. YinYang Bipolar Quantum Superposition
Schrödinger’s Cat has remained a paradox for many decades. An equilibrium-based bipolar quantum geometry (BQG) is proposed based on the YinYang bipolar complementarity principle for resolving the paradox [16] - [18] [22] - [24] . The equilibrium-based axiomatic formulation is revised and introduced as following:
Definition 1. A bipolar dynamic equilibrium is a process of bipolar interaction and state change among bipolar equilibrium, non-equilibrium, and eternal equilibrium states of any action-reaction pair or any collection of such pairs.
Definition 2. A bipolar quantum agent (BQA) is a bipolar dynamic equilibrium. A global bipolar dynamic equilibrium may subsume local ones and a non-elementary BQA may consist of elementary BQAs (Adapted from [16] [21] - [24] ).
Definition 3. A BQA is said equilibrium-based if it adapts to an equilibrium state under a closed world condition or without external disturbance.
Postulate 1. If an elementary particle or BQA is in a non-equilibrium negative state that can be characterized with the bipolar value (−1,0), its antiparticle must be a BQA in another non-equilibrium state that can be characterized with the bipolar value (0,+1) and the two in a pair without annihilation must be a BQA in an equilibrium state which can be characterized with the bipolar value (−1,+1). The non-existence or annihilation of the particle-antiparticle pair can be characterized with an eternal equilibrium state with the bipolar value (0,0).
Postulate 2. If an elementary particle is its own antiparticle, the BQA must have distinct states that can be characterized as negative (−1,0), positive (0,+1), bipolar equilibrium (−1,+1) and eternal equilibrium (0,0), respectively.
Postulate 3. A BQA as a bipolar dynamic equilibrium can emerge from the Yin and Yang of Nature or from other elementary BQAs and can submerge back to the Yin and Yang or other elementary BQAs.
Definition 4. Bipolar quantum geometry (BQG) has three shape-free and quadrant-irrelevant dimensions: the Yin and the Yang dimensions are the two reciprocal and interdependent bipolar opposites from which a third dimension―bipolar dynamic equilibrium as a bipolar quantum superposition of the Yin and Yang dimensions- can emerge and submerge.
Definition 5. A geometry with complete background independence must satisfy the minimum set of conditions: 1) it is shape-free, quadrant irrelevant and spacetime transcendent; 2) it supports reductionism, emergence and submergence; 3) it is ubiquitous.
It is proven that BQG satisfies the conditions of complete background independence [22] - [24] . Figures 3(a)-(c) show a sketch of BQG as an extension of YinYang bipolar geometry with a comparison to Dirac’s quantum superposition in Figure 3(d) [29] .
![]()
Figure 3. A comparison: (a) Magnitude model of BQG; (b)-(c) Background independent property of BQG; (d) Dirac’s quantum superposition.
deemed a real-valued extension of BDL on one hand or a bipolar dynamic generalization of fuzzy logic (FL) [33] for bipolar probabilistic reasoning on the other hand. BQLA can be deemed an algebraic extension of BDL and BDFL on one hand or a bipolar dynamic generalization of linear algebra (LA) on the other hand. A comparison of the generalizations with the generalized reveals that
§ BL is truth-based without physical semantics and BDL is equilibrium-based with both logical and physical semantics. BDL generalizes BL from the truth-based domain or Boolean lattice L = {0,1} to the equilibrium-based domain or quantum lattice B1 = {−1,0} 0,+1}. BL is not a causal logic. BDL is a formal causal logic (see Appendix).
§ BDFL is a bipolar dynamic generalization of FL from the truth-based domain or fuzzy lattice LF = [0,1] to the equilibrium-based domain or quantum lattice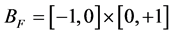 ―a bounded real-valued bipolar causal set.
―a bounded real-valued bipolar causal set.
§ BQLA is a bipolar dynamic generalization of linear algebra (LA) from the truth-based domain or lattice L∞ = [−∞,+∞] to the equilibrium-based domain or quantum lattice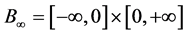 ―an unbounded real- valued causal set.
―an unbounded real- valued causal set.
§ Without bipolarity BL, FL and LA are inadequate for the direct representation of a BQA with equilibrium and non-equilibrium states.
§ Without a shred of dynamics, truth-values cannot form a causal set like B1, BF and B∞.
§ BDL, BDFL and BQLA subsume BL, FL and LA because any being or truth in spacetime must exist in a bipolar dynamic equilibrium of input-output information or negative-positive energies.
§ BL, FL and LA can be used together with BDL, BDFL and BQLA as long as equilibrium or non-equilibrium conditions are not violated.
BDL leads to a number of simplifications. Quantum superposition in Dirac’s bra-ket notation (Equation (1)) can be simplified to Equation (2a) in bipolar logical form. Quantum entanglement can be logically defined by Equation (2b). The simplification makes it possible to avoid complex number coefficients. Since BQG is background independent, vertical (v) and horizontal (h) as two direct opposites in a bipolar dynamic equilibrium each can be negative or positive, respectively. Without bipolarity, however, Dirac’s quantum superposition principle does not account for bipolar complementarity, does not support emergence and submergence through bipolar interaction, and stopped short of evolving to a logical definition for quantum superposition and entanglement. BQG and BDL, on the other hand, provides a geometrical and logical basis for both quantum superposition and quantum entanglement.
Bipolar Logical Definition of Generic Quantum Superposition:
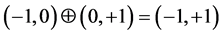 ; (2a)
; (2a)
Bipolar Logical Definition of Generic Quantum Entanglement:
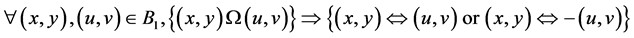 . (2b)
. (2b)
A key element of BDL is bipolar universal modus ponens (BUMP)―a bipolar dynamic generalization of modus ponens (MP) which states that, 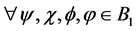 ,
,
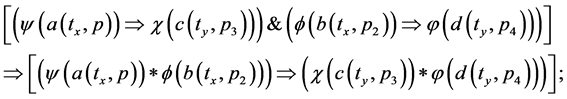 (2c)
(2c)
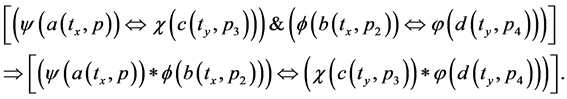 (2d)
(2d)
In Equation (2c), 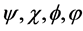 are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and
are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and
space p is therefore more specific. BUMP reads: If 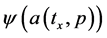 implies
implies 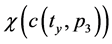 and
and ![]() implies
implies![]() , then the bipolar interaction
, then the bipolar interaction ![]() implies that of
implies that of
![]() . If the bipolar implication operator Þ is replaced with the bipolar equivalence operator Û, BUMP becomes a logical form of quantum entanglement as shown in Equation (3b). The logical form of bipolar quantum entanglement qualifies BDL as a causal logic for equilibrium-based bipolar deduction. On the other hand, BQG and BDL supports the fundamental concept of spacetime emergence as a bipolar quantum superposition or entanglement of Nature’s Yin and Yang in a dynamic equilibrium or harmony.
. If the bipolar implication operator Þ is replaced with the bipolar equivalence operator Û, BUMP becomes a logical form of quantum entanglement as shown in Equation (3b). The logical form of bipolar quantum entanglement qualifies BDL as a causal logic for equilibrium-based bipolar deduction. On the other hand, BQG and BDL supports the fundamental concept of spacetime emergence as a bipolar quantum superposition or entanglement of Nature’s Yin and Yang in a dynamic equilibrium or harmony.
2.4. Logical Exposition of Dirac 3-Polarizer Experiment―A Vindication
It is shown in [22] - [24] that a single incoming polarized photon can be logically channeled through the three polarizers in Dirac’s experiment with BDL in BQG regardless of quantum uncertainty or probability. Since photon is its own antiparticle, following Postulates 1 and 2 we make the background independent and quadrant irrelevant assumptions: 1) a vertically polarized photon state is a positive state (0,+1); 2) a horizontally polarized photon state is a negative state (−1,0); (3) a diagonally polarized photon state is a bipolar equilibrium state (−1,+1); (4) (0,0) stands for no light.
1) Let vertical polarizers A and B be both in state (0,+1) or let two horizontal polarizers be both in state (−1,0), logically, we have ![]() or
or![]() , respectively. Light gets through A&B in both cases.
, respectively. Light gets through A&B in both cases.
2) Let vertical polarizer A be in state (0, +1) and horizontal polarizer B in state (−1, 0), ![]() No light gets through A&B.
No light gets through A&B.
3) Let diagonal polarizer C (45˚) be in bipolar equilibrium state (−1,+1), the question is how a single photon can logically get through A, C and B if C is slipped between A and B.
Is there a bipolar conjunctive operator in BDL that allows a single photon to get through the three polarizers in Case (c)? The problem can be formulated as: What is the unknown operator *such that
1) ![]() or
or
2)![]() ?
?
If the Boolean operator & takes effect in the place of *, light can only get through the diagonal polarizer C but cannot get through B as we have:
![]() or (3a)
or (3a)
![]() (3b)
(3b)
BDL does, however, have another conjunctive &- such that ![]() (see Appendix). Substitute * in 1) and 2) with &- we have:
(see Appendix). Substitute * in 1) and 2) with &- we have:
![]() ; or (3c)
; or (3c)
![]() . (3d)
. (3d)
The results in Equations (3a)-(3d) are supported with well-known experimental results for the quantum superposition principle [29] . Thus, the logical exposition constitutes a reconstruction of quantum mechanics with a geometry of light and a logic of polarized photons. The reconstruction is shown to be a point of fundamental departure from quantum mechanics in the remaining sections.
2.5. Bipolar Probability―A Vindication of Bipolar Quantum Superposition
While Dirac tells us that “diagonally polarized photon can be represented as a superposition of vertical and horizontal states, with complex number coefficients that represent probability amplitudes,” the nature of superposition has never been logically clarified. It is shown in [22] - [24] that the nature of quantum superposition is bipolar dynamic equilibrium or bipolar quantum superposition.
Figure 4 and Figure 5 provide a geometrical comparison of the two different approaches to quantum superposition by Dirac and by the YinYang bipolar quantum geometry. In Figure 4 the area of a square becomes a conversion from complex number coefficient to the probability of a photon that can pass a polarizer. While complex numbers provide a powerful computational tool in Hilbert space, it makes quantum superposition
![]()
Figure 4. Quantum mechanical interpretation of quantum superposition without bipolarity and logically definable causality.
![]()
Figure 5. Equilibrium-based logical interpretation of quantum superposition with bipolarity and logically definable causality in BQG.
mysterious without a unique logical system for equilibrium-based bipolar dynamic reasoning. Thus, the analytical power of the quantum mechanical interpretation of superposition is compromised by the complex number coefficients.
Figure 5 provides a picture for the equilibrium-based logical interpretation of quantum superposition. In the new interpretation, all quantum states are represented by bipolar scalar values of the Yin and the Yang in equilibrium or non-equilibrium. The bipolar scalar representation provides a basis for BDL, BDFL and BQLA for logical, probabilistic and algebraic reasoning and computation on quantum superposition, emergence and submergence.
For instance, the probability for a vertically prepared photon to pass the diagonal polarizer C as a square of a
complex number coefficient is![]() . But Figure 4 can be easily represented in Figure 5 by an equili-
. But Figure 4 can be easily represented in Figure 5 by an equili-
brium-based bipolar logic or probability value (−1/4, +1/4). Evidently, we have![]() . In
. In
general, the bipolar probability amplitude of a bipolar variable ![]() can be defined as
can be defined as![]() . The scalar probability values −1/4 and +1/4 are much simpler and more meaningful than complex coefficients when and where Hilbert space is not required for analytical purposes. Thus, the bipolar equilibrium-based approach leads to an analytical paradigm of quantum superposition.
. The scalar probability values −1/4 and +1/4 are much simpler and more meaningful than complex coefficients when and where Hilbert space is not required for analytical purposes. Thus, the bipolar equilibrium-based approach leads to an analytical paradigm of quantum superposition.
Furthermore, it is clear from Figure 5 that the diagonally prepared photons C present an emergence from h and v―the Yin and Yang. On the other hand, c submerged to v and h (after polarizer B) in the experiment. It can be argued, however, that the emergence and submergence are also represented in Figure 4 with complex number coefficients. The counter argument is that, without bipolarity, there would be no bipolar interaction, no BDL, no BQG, no logically definable quantum emergence and submergence.
The comparison further confirms that YinYang bipolar complementarity is the most fundamental complementarity which may lead to the emergence and submergence of a bipolar quantum superposition. On the other hand, the real and imaginary dimensions of complex numbers are not most fundamental because they do not support background independent bipolar interaction and emergence.
3. G-CPT Symmetry
3.1. Logical Basis
According to the bipolar complementarity principle, space-time and particle-wave complementarities are less fundamental concepts subject to bipolar complementarity and bipolar dynamic equilibrium. Thus, the 3-D information of particle-wave in Hilbert space are ever changing phenomenon because spacetime is ever changing due to bipolar dynamic equilibrium. We need a point of departure from spacetime relativity and particle-wave duality. While BDL is such a point of logical departure, BQLA extends BDL to a point of mathematical departure from bra-ket notations in Hilbert space. The result is a multidimensional bipolar equilibrium-based unification of energy and information for symmetry and regulation of multiple BQAs in the background independent ubiquitous BQG.
Given bipolar quantum agent![]() , we have Equations (4a)-(4m) (adapted from [16] [21] [33] [34] ):
, we have Equations (4a)-(4m) (adapted from [16] [21] [33] [34] ):
§ The Yin or negative energy/information of e:![]() ; (4a1)
; (4a1)
§ The absolute Yin energy/information of e:![]() ; (4a2)
; (4a2)
§ The Yang or positive energy/information of e:![]() ; (4b1)
; (4b1)
§ The absolute Yang energy/information of e:![]() ; (4b2)
; (4b2)
§ Equilibrium state of e: ![]() when
when![]() ; (4c)
; (4c)
§ Non-equilibrium state of e: ![]() when
when![]() ; (4d)
; (4d)
§ Eternal equilibrium state of e:![]() ; (4e)
; (4e)
§ Bipolar energy/information of e:![]() ; (4f)
; (4f)
§ Imbalance of e:![]() ; (4g)
; (4g)
§ Balance of e:![]() ; (4h)
; (4h)
§ Harmony of e:![]() ; (4i)
; (4i)
§ Bipolar superposition in scalar form:![]() ; (4j)
; (4j)
§ Bipolar superposition in vector form:![]() ; (4k)
; (4k)
§ Superposition magnitude:![]() . (4l)
. (4l)
§ Equilibrium-Based Unification of energy/information:
![]() ; (4m)
; (4m)
The unification of energy/information provides a necessary condition for an equilibrium-based energy/infor- mation conservational generalization of CPT symmetry. Elementary energy/information measures can be extended to system energy/information measures with BQLA for bipolar regulation. Each row, column, or a whole bipolar matrix can have negative, positive and bipolar energy/information with absolute total and balance. While BDL is logical but not fully mathematical, BQLA leads to an algebraic unification of bipolar energy/informa- tion that in turn leads to formal algebraic definitions of equilibrium and harmony―a unifying concept for both the classical and quantum worlds.
![]() , positive scalar a and negative scalar b, we have Equation (5a)-(5b):
, positive scalar a and negative scalar b, we have Equation (5a)-(5b):
Bipolar Algebraic Addition:![]() ; (5a)
; (5a)
Bipolar Algebraic Multiplication:![]() ; (5b)
; (5b)
Linear multiplication or division:![]() ; (5c)
; (5c)
Bipolar Conjunctive Multiplication:![]() ; (5d)
; (5d)
Bipolar Disjunctive Multiplication:![]() . (5e)
. (5e)
With Equation (5a)-(5b), system level bipolar quantum superposition of multiple BQAs can be mathematically characterized with bipolar matrix addition and multiplication using BQLA similarly as in LA. We prove in what follows that quantum superposition with bipolar addition and multiplication makes it possible to have a fundamental departure from Dirac’s Bra-ket superposition in Hilbert space for systematic analysis of multiple BQA superposition.
Theorem 1. With background independence, bipolar addition is essentially bipolar quantum superposition of two BQAs into one in BQG.
Proof. Given BQAs A = (x, y) and B = (u, v), following Equation (4m) and Equation (5) we have:
![]() (6)
(6)
Since A and B are both bipolar vectors in BQG, Hilbert space vector addition is converted to scalar addition in Equation (6) as illustrated in Figure 6 with the same magnitude ![]() .
. ![]()
Theorem 2. With background independence, bipolar multiplication can, under certain condition, be used to characterize equilibrium-based BQA composition into a new BQA through bipolar interaction and superposition in BQG.
Theorem 3. With background independence, bipolar multiplication converts vector multiplication from Hilbert space to algebraic computation in BQG with the preservation of vector magnitude and without the preservation of background dependent information.
Proof. It follows from that
![]()
![]() (see Figure 6).
(see Figure 6). ![]()
Theorem 4. With background independence, bipolar matrix multiplication can, under certain condition, be used for characterizing the composition of a set of BQAs into another set of BQAs through bipolar interaction and quantum superposition in BQG.
![]()
Figure 6. Conversion from Hilbert space to bipolar space with vector magnitude preservation.
Proof. Given the square bipolar matrix ![]() with two BQAs A and B, let A = (x, y) and B = (u, v); given
with two BQAs A and B, let A = (x, y) and B = (u, v); given
the column bipolar matrix ![]() with two BQAs C and D, let C = (o, p) and B = (q, r); a new BQA E can be
with two BQAs C and D, let C = (o, p) and B = (q, r); a new BQA E can be
formed where
![]()
Thus, the multiplication of a row BQA matrix and a column BQA matrix results in a new BQA―an ensemble or composite of component BQAs in a superposition. The result of each such row by column multiplication results in a newly composed BQA. An n × n bipolar square matrix multiplied by an n × 1 bipolar column matrix results in n new column matrix of BQAs which can be deemed a set of BQAs or a single composite BQA. ![]()
3.2. Unification of Logical Linearity and Physical Nonlinearity
All agents are input/output (I/O) systems that can be classified as linear or nonlinear. If we apply input x to a dynamic system and obtain output y, scaling input x may give a scaled y such as the input ax leads to ay, where a is a scalar. When this property is true, we say that the I/O system is a linear system. Otherwise, it is nonlinear.
Similarly, a logic is said a linear logic if it satisfies the distributive law such as ![]() where A, B or C assumes a truth value 0 or 1 which can be deemed a scalar for false or true, respectively. Thus, Boolean logic can be said a linear logic. A generalization of Boolean logic to intuitionistic logic can be achieved by a linear logic [34] - [36] .
where A, B or C assumes a truth value 0 or 1 which can be deemed a scalar for false or true, respectively. Thus, Boolean logic can be said a linear logic. A generalization of Boolean logic to intuitionistic logic can be achieved by a linear logic [34] - [36] .
Logical linearity and physical nonlinearity can be deemed a duality. It is unclear, however, how to unify logical linearity and physical nonlinearity for nonlinear dynamic logical reasoning of quantum superposition. Is there a dynamic logic that is logically linear but physically nonlinear?
BDL, BDFL and BQLA [16] as equilibrium-based generalizations of BL [32] , FL [33] and LA, respectively, are bipolar dynamic in nature due to bipolar interaction. Whether they are linear or nonlinear is a matter of debate. While BDL was said a nonlinear bipolar dynamic generalization of BL [16] - [21] , it can be argued that it is nothing more than a hyperspatial linear extension of BL. This argument is a strong one because bipolar distributivity of Ä and Å as well as & and Å, the very definition of linearity, is indeed maintained with BDL (see Appendix Table A2).
A further examination, however, reveals that, due to equilibrium-based bipolar dynamic interaction, BDL presents a unification of logical and physical systems. Since all beings must exist in certain bipolar dynamic equilibrium of input-output (I/O) or negative-positive energies/information, the bipolar operators can characterize different bipolar dynamic interactions and can change an equilibrium state to a non-equilibrium state with nonlinear bipolar dynamic behaviors. For instance, a(input, output) or a(−pole, +pole) is a linear scaling if a is a scalar; (−1,0) &-( −1,+1) = (0,+1) is logically linear but physically non-linear because a bipolar variable is not a scalar and a bipolar operator does not scale. Thus, logically, the binary operators of BDL are linear or bilinear that provide a basis for the soundness of the logic; physically it has nonlinear dynamics embedded and is inherently nonlinear. This is fundamentally different from truth-based linear or bilinear systems which do not assume equilibrium-based physical semantics.
With the logical basis, BQLA borrows the forms of classical linear algebra but performs nonlinear bipolar dynamic operations in bipolar dynamic equilibrium domains. As a nonlinear bipolar dynamic generalization of LA, BQLA is to BDL as LA is to BL or BQLA is to LA as BDL is to BL. With the unification of logical linearity and physical non-linearity, an information conservational unification of CPT symmetry and CP violation under bipolar dynamic equilibrium is made possible.
3.3. Information Conservational Multiagent Cellular Automata Unification of Quantum Emergence and Submergence
The concepts of bipolar elementary energy and information laid a basis for modeling bipolar quantum superposition of multiple BQAs as a multidimensional dynamic equilibrium with BQLA. Figure 7 shows that two or more bipolar variables can be integrated into a multidimensional bipolar quantum superposition.
Electron and positron form a typical bipolar particle-antiparticle pair. It is believed that matter and antimatter once existed in near perfect counterbalance immediately after the big bang but antimatter vanished without a trace on a cosmic scale-one of the greatest mysteries of the universe. Today, antimatter does not exist normally, at least on Earth, but we know that it is real because positron has been discovered [37] . As the most fundamental example of the materialization of energy, electron-positron pair production has been accurately described by quantum electrodynamics (QED)-the jewel of physics [38] [39] . Now, positron is applied in nuclear medicine.
Since an electron carries one unit of negative charge (−1), a negative charge is generally deemed an electron. On the other hand, a positron carries one unit of positive charge (+1) but a positive charge is not deemed a positron. This conceptual imbalance can trace its origin to Dirac’s prediction of positron [40] . Before his prediction, he once explored the possibility of proton being an island of positively charged electron [41] . Dirac acknowledged the problem that a proton has a much greater mass than an electron, but expressed “hope” that a future theory would resolve the issue. It is said ( [42] : p. 46) that Robert Oppenheimer argued strongly against the proposal because, in that case, the hydrogen atom would rapidly self-destruct in an annihilation. Persuaded by Oppenheimer’s argument, Dirac predicted the existence of an as-yet unobserved particle that he called an “anti-electron” that would have the same mass as an electron and would mutually annihilate upon contact with an electron [40] .
Now, it is well-known that, in positron emission or beta plus decay (β+ decay), a proton is converted to a neutron while releasing a positron (β+) and an electron neutrino. On the other hand, in beta minus decay (β− decay), a neutron turns into a proton and the nucleus emits an electron (β−) and an antineutrino. To certain extent, positron emission justifies proton being an island of positron as Dirac originally suggested. The problem is that proton consists of quarks [43] and does not contain a positron according to the standard model. Here, we have the question whether the quark formation of a proton is Nature’s “encryption” mechanism to conceal a positron within a proton to prevent it from annihilation with an electron―a possible interpretation to the matter-antimatter
![]()
Figure 7. Multidimensional equilibrium of bipolar quantum agents (adapted from [16] ).
asymmetry. According to Richard Feynman, the “encryption” or hidden positron idea was suggested by John Wheeler in 1940 (cf. [44] ).
In any case, matter and antimatter atoms are formed with particles and antiparticles in certain combinations. The quarks of a proton do carry a total of one positive charge and a proton does emit a positron in β+ decay. In terms of negative-positive energy/information conservation, the hidden positron hypothesis is logically a valid theory. The theory has led to an equilibrium-based axiomatization of physics with BDL and BQLA in BQG [16] ―a minimum but most general solution to Hilbert Problem 6 [45] .
Postulate 4. An antiparticle can be logically encrypted and physically concealed or insulated within a particle and vice versa.
Postulate 5. A positron is logically encrypted and physically concealed within a proton to prevent it from annihilation with an electron; an electron is logically encrypted and physically concealed within an antiproton to prevent it from annihilation with a positron.
Based on the above postulate, we have
Definition 6 (Matter and Antimatter Emergence and Submergence). A matter or antimatter atom is logically a set of electron-positron pairs or BQAs insulated from annihilation and regulated by the nucleus of the atom. When N electron-positron pair(s) as component BQAs![]() , N > 0, are organized by its nucleus into a matter or antimatter atom to form a composite BQA, we have matter or antimatter emergence. When a matter or antimatter atom split or decay into subatomic particles and/or antiparticles, we have matter or antimatter submergence.
, N > 0, are organized by its nucleus into a matter or antimatter atom to form a composite BQA, we have matter or antimatter emergence. When a matter or antimatter atom split or decay into subatomic particles and/or antiparticles, we have matter or antimatter submergence.
Theorem 5. Matter or antimatter emergence can be characterized as a multidimensional quantum superposition with a bipolar quantum cellular automaton interpretation of quantum mechanics.
Proof. Given N electron-positron pair(s) insulated from annihilation as component BQAs![]() , N > 0, the nucleus as the organizational center of the atom can be characterized by a bipolar quantum logic gate matrix M and the emergence of an atom can be defined as the self-organization of the component BQAs around the nucleus into a bipolar quantum cellular automaton (BQCA)―a composite BQA E as shown in Equation (7).
, N > 0, the nucleus as the organizational center of the atom can be characterized by a bipolar quantum logic gate matrix M and the emergence of an atom can be defined as the self-organization of the component BQAs around the nucleus into a bipolar quantum cellular automaton (BQCA)―a composite BQA E as shown in Equation (7).
BQCA in BQLA:![]() ; (7a)
; (7a)
BQCA Power Law:![]() . (7b)
. (7b)
In Equation (7), M(t) is an N by N bipolar quantum logic gate matrix that characterizes the nucleus bipolar regulatory energy/information at time t; E is an N by 1 bipolar matrix characterizing the bipolar energy/information of a column matrix of N BQAs such as the electron-positron pairs of an atom at time t. Equation 7(a) is based on Equation (5a)-(5b). It defines system level quantum superposition with BQLA matrix multiplication; Equation 7(b) defines a bipolar quantum power law. Time is introduced into the equations (Note: Although BQG is background independent, it subsumes spacetime, time and/or space can be added as needed).
Thus, a BQCA characterizes a multidimensional bipolar dynamic equilibrium emerged from bipolar quantum superposition without annihilation due to the concealment (See Postulates 4 and 5). ![]()
Figure 8 shows a bipolar equilibrium-based unification of matter and antimatter atoms as a BQCA. Matter- antimatter emergence can be deemed a result of BQCA self-organization and unification of multiple BQAs in BQG. The unification is realized in the background independent BQG. It can be posited that spacetime emergence is fundamentally matter-antimatter emergence. It is shown that the BQCA model also leads to the unification
![]()
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 8. (a) Matter atom as bipolar quantum agent; (b) Antimatter atom as bipolar quantum agent; (c) Bipolar equilibrium-based unification of matter and antimatter into a bipolar cellular automaton (adapted from [16] [17] ).
of wave and particle [17] [21] [46] . Thus, not only BQG qualifies to be the geometry of light, it is also qualifies to be the geometry of Nature. It opened a new direction for exploring a number of frontiers in modern science [16] - [26] [47] - [53] .
With BQCA, a quantum agent can be regulated to maintain energy/information conservation. When the absolute total energy of each row ![]() and that of each column
and that of each column ![]() of the regulatory matrix M(t) equals 1.0, M(t) is defined as a generalized unitary bipolar quantum logic gate matrix extended from integer domain to decimal domain [18] [21] . Such a quantum logic gate exhibits energy/information conservation functionality which can also be scaled from logical and physical level to biological, mental and social worlds [16] - [26] [54] - [59] .
of the regulatory matrix M(t) equals 1.0, M(t) is defined as a generalized unitary bipolar quantum logic gate matrix extended from integer domain to decimal domain [18] [21] . Such a quantum logic gate exhibits energy/information conservation functionality which can also be scaled from logical and physical level to biological, mental and social worlds [16] - [26] [54] - [59] .
While the condition that the absolute total energy and/or information of each row ![]() equals 1.0 is necessary for uniform energy/information conservation and distribution at both system and elementary levels in an isotropic quantum world, the condition is unnecessary for non-uniform energy and/or information conservation, regeneration, degeneration and distribution. It is therefore not applicable in an anisotropic classical world. For instance, the condition is not applicable for the emergence in a quantum world and submergence to a classical world. Thus, we reserve the original definition for an isotropic quantum world and redefine energy/infor- mation conservation, degeneration and regeneration with a relaxed condition for a more general category of application domains that entail nuclear decay and fission, biological mutation and evolution, natural degeneration and regeneration, mental fusion and fission, social dynamics and other anisotropic changes [16] - [26] [54] - [59] .
equals 1.0 is necessary for uniform energy/information conservation and distribution at both system and elementary levels in an isotropic quantum world, the condition is unnecessary for non-uniform energy and/or information conservation, regeneration, degeneration and distribution. It is therefore not applicable in an anisotropic classical world. For instance, the condition is not applicable for the emergence in a quantum world and submergence to a classical world. Thus, we reserve the original definition for an isotropic quantum world and redefine energy/infor- mation conservation, degeneration and regeneration with a relaxed condition for a more general category of application domains that entail nuclear decay and fission, biological mutation and evolution, natural degeneration and regeneration, mental fusion and fission, social dynamics and other anisotropic changes [16] - [26] [54] - [59] .
Definition 7. Given a regulatory bipolar matrix M(t) defined on BF such that![]() , 1) if the absolute total energy/information of each column
, 1) if the absolute total energy/information of each column ![]() (but not necessarily each row) equals 1.0, M(t) is defined as an energy/information conservational bipolar quantum logic gate matrix; 2) if the absolute total energy/information of each column
(but not necessarily each row) equals 1.0, M(t) is defined as an energy/information conservational bipolar quantum logic gate matrix; 2) if the absolute total energy/information of each column ![]() (but not necessarily each row) is greater than 1.0, M(t) is defined as an energy/information regeneration bipolar quantum logic gate matrix; if the absolute total energy/information of each column
(but not necessarily each row) is greater than 1.0, M(t) is defined as an energy/information regeneration bipolar quantum logic gate matrix; if the absolute total energy/information of each column ![]() (but not necessarily each row) is less than 1.0, M(t) is defined as an energy/information degeneration bipolar quantum logic gate matrix.
(but not necessarily each row) is less than 1.0, M(t) is defined as an energy/information degeneration bipolar quantum logic gate matrix.
Theorem 6. The law of energy/information conservation/preservation, degeneration and regeneration:
1) An energy/information conservational bipolar quantum logic gate matrix exhibits holistic energy/informa- tion conservation regulatory functionality at the system level. That is, if ∀j, ![]() , we have
, we have
![]() . (8a)
. (8a)
![]() . (8b)
. (8b)
2) An energy/information regeneration bipolar quantum logic gate matrix exhibits holistic energy/informa- tion regeneration regulatory functionality at the system level. That is, if ∀j, ![]() , we have
, we have
![]() . (8c)
. (8c)
![]() . (8d)
. (8d)
3) An energy/information regeneration bipolar quantum logic gate matrix exhibits holistic energy/informa- tion degeneration regulatory functionality at the system level. That is, if ∀j, ![]() , we have
, we have
![]() . (8e)
. (8e)
![]() . (8f)
. (8f)
Proof. 1) If ∀i,j, ![]() , it enables 100% of the energy/information be transferred from E(t) to
, it enables 100% of the energy/information be transferred from E(t) to![]() . 2) If ∀i,j,
. 2) If ∀i,j, ![]() , it enables more than 100% of the energy/information be transferred from E(t) to
, it enables more than 100% of the energy/information be transferred from E(t) to![]() . 3) If ∀i,j,
. 3) If ∀i,j, ![]() , it enables less than 100% of the energy/information be transferred from E(t) to
, it enables less than 100% of the energy/information be transferred from E(t) to![]() .
. ![]()
It can be further postulated that energy/information degeneration or regeneration increases or decreases energy/information of the environment, respectively. Thus, bipolar energy/information conservation (Equations 8a-8b) can be deemed a global dynamic equilibrium process with local non-equilibrium states. It can be further posited a necessary condition for quantum coherence. Under this condition, local CP-violation can lead to harmonic oscillations among a set of BQAs. This can be posited another condition for coherence. Global energy/information conservation with local CP-violation is illustrated as follows:
![]() ;
;
Column energies of![]() :
:
![]() ;
;
![]() ;
;
Global energy/information conservation of ![]() and
and![]() :
:
![]() ;
;
![]() .
.
Figures 9(a)-(d) show examples of bipolar energy/information conservation, regeneration, degeneration and oscillation, respectively, with particle-wave unification. Each bipolar wave form is also a BQA = (x,y) or a bipolar subatomic particle.
Theorem 7. Quantum decoherence and collapse can be logically unified under quantumsubmergence of a multidimensional quantum superposition with a bipolar quantum cellular automaton interpretation of quantum mechanics.
Proof. Based on Equation (8), when![]() , a BQCA can be regulated for energy/information increase. When
, a BQCA can be regulated for energy/information increase. When![]() , quantum coherence emerges in a delegate bipolar dynamic equilibrium/har- mony. After then, any of the two conditions of
, quantum coherence emerges in a delegate bipolar dynamic equilibrium/har- mony. After then, any of the two conditions of ![]() or
or ![]() will cause the submergence of the coherence into decoherence or collapse.
will cause the submergence of the coherence into decoherence or collapse. ![]()
3.4. Bipolar Dynamic Equilibrium―The Essence of Being and Causality
Definition 8. A BQA in the logical form (x,y) is said a primitive BQA. A BQA in the BQCA matrix form ![]() is said a multiagent or composite BQA.
is said a multiagent or composite BQA.
Definition 9. Given two BQAs A1 and A2, primitive or composite, we say A1 and A2 are in a 2-party quantum entanglement, denoted A1W A2, if ![]() or
or![]() , where the bipolar equivalence operator Û is generalized from its logical equivalence (Appendix Table A1) to matrix equivalence. Formally, we have Equation (9a)-(9c):
, where the bipolar equivalence operator Û is generalized from its logical equivalence (Appendix Table A1) to matrix equivalence. Formally, we have Equation (9a)-(9c):
![]() (9a)
(9a)
![]() (9b)
(9b)
![]() (9c)
(9c)
It should be noted that, for any bipolar agent A we have![]() . Thus, the negation operation (-) is energy-information conservational―a distinguishing property of BDL, BQLA and BQCA which provide a mathematical basis for CP-violation while maintaining energy information conservation. On the other hand, since
. Thus, the negation operation (-) is energy-information conservational―a distinguishing property of BDL, BQLA and BQCA which provide a mathematical basis for CP-violation while maintaining energy information conservation. On the other hand, since![]() , the complement operation (Ø) is, in general, not energy-information conservational except for certain symmetrical cases [18] .
, the complement operation (Ø) is, in general, not energy-information conservational except for certain symmetrical cases [18] .
Theorem 8. Without bipolar coexistence of negative-positive energies/information, bipolar interaction and energy/information conservation would be impossible with CP-violation.
Proof. First, without bipolar coexistence of negative-positive energies/information, bipolar interaction and CP-violation cannot be fully represented. Secondly, without such bipolar coexistence, the absolute total energy/information equality ![]() would be impossible.
would be impossible. ![]()
While truth has been deemed the essence of being since Aristotle, without bipolarity truth-based logic and linear algebra are incapable of bipolar causal interaction, self-organization, and dynamic regulation for bipolar emergence and submergence due to bipolar cancelation. For instance,
![]() ;
;![]() ;
;![]() .
.
The above examples clearly show that, without bipolar regulation, bipolar equilibrium-based emergence and submergence is impossible. Of course, we can attempt to use a positive regulation matrix. But a positive matrix does not show bipolar interaction and balancing cause-effect relation toward a bipolar dynamic equilibrium, non- equilibrium or oscillating state. For instance,
![]() .
.
From the above, it is clear that (−,+) bipolarity is a key for bipolar causality, bipolar quantum superposition and bipolar quantum entanglement. It provides a holistic, unitary, and analytical framework for the complex interaction and regulation of quantum agents. While quantum mechanics heavily relies on probability and do not lend itself as an analytical system, the analytical nature of the bipolar equilibrium-based approach provides a geometrical and logical basis of quantum mechanics, quantum gravity, quantum emergence and submergence for the analysis of coherence, decoherence and/or collapse.
Theorem 8 shows that, different from other alternative interpretations of quantum mechanics, BQCA as a point of departure from quantum mechanics is a fundamental one. The tradeoff is the less fundamental 3-D space which emerges from bipolar interaction in a forever changing state, the gain is the most fundamental equilibrium-based background-independent bipolar complementarity for logically definable causality of local and non-local quantum agent emergence and submergence toward an equilibrium-based computing paradigm of quantum agents and quantum intelligence [21] .
Theorem 9. Any natural agent can be characterized as a BQA or BQCA and any BQA or BQCA can be characterized as either a vector or point in BQG.
Proof. It follows from that any being in the universe including the universe itself can be characterized as a bipolar dynamic equilibrium of negative-positive energies. Andgiven any BQA or BQCA variable A, we have
![]() and
and![]() , where
, where ![]()
![]()
3.5. Information Conservational Unification of CPT Symmetry and CP Violation
While BDL provides a basis for generic quantum superposition and entanglement, BQLA and BQCA provides a computational basis for multiagent quantum superposition and entanglement. In this section we present an axiomatic formulation of G-CPT symmetry of multiple BQAs for quantum emergence and submergence.
Definition 10. 1) G-CPT Symmetry is an equilibrium-based generalization of CPT symmetry where electromagnetic particle-antiparticle and gravitational action-reaction bipolarities are unified into a dynamic equilibrium of bipolar coexistence. 2) Under G-CPT symmetry, any unregulated or asymmetrical movement of an object constitutes a G-CP-violation or G-T-violation.
For instance, the apparatus movement in an asymmetrical quantum measurement can be deemed unregulated. Natural and symmetrical movements of celestial objects, on the other hand, can be deemed regulated by G-CPT symmetry. Thus, Definition 10 prompted the entry of G-CP-violation into causal analysis of quantum decoherence and collapse.
Theorem 10. (2-party entanglement emergence and submergence). Given BQAs ![]() and
and![]() , the quantum entanglement of the two BQAs is fundamentally the emergence of a local quantum coherence coupled or synchronized into a global one of the same type. Two necessary conditions to keep the two agents in coherence and prevent them from submergence or decoupling are:
, the quantum entanglement of the two BQAs is fundamentally the emergence of a local quantum coherence coupled or synchronized into a global one of the same type. Two necessary conditions to keep the two agents in coherence and prevent them from submergence or decoupling are:
1) Keeping ![]() and
and ![]() identical or in opposite polarity at all times for all i and j, formally, we have Equations (10a)-(10c):
identical or in opposite polarity at all times for all i and j, formally, we have Equations (10a)-(10c):
![]() or (10a)
or (10a)
![]() (10b)
(10b)
2) Keeping both M1(t) and M2(t) energy/information conservational at all times, formally,
![]() (10c)
(10c)
Proof. To have![]() , we must have the equivalence of either
, we must have the equivalence of either ![]() or
or ![]() . If the corresponding elements
. If the corresponding elements ![]() and
and ![]() are not identical or in opposite polarity in both energy and charge-parity at all times and for all i and j, the equivalence condition of two entangled BQAs will be violated and submergence of the entanglement will occur. On the other hand, if M1(t) and M2(t) are not both energy/information conservational at all times, energy/information increase or decrease must be due to disturbance that can cause the submergence of the entanglement as well.
are not identical or in opposite polarity in both energy and charge-parity at all times and for all i and j, the equivalence condition of two entangled BQAs will be violated and submergence of the entanglement will occur. On the other hand, if M1(t) and M2(t) are not both energy/information conservational at all times, energy/information increase or decrease must be due to disturbance that can cause the submergence of the entanglement as well. ![]()
It should be remarked that Theorem 10 provides some necessary conditions for quantum coherence that may not be sufficient. For instance, ![]() may also requires other conditions such as that both BQAs be involved in the same harmonic oscillations. Such harmonic oscillation is made possible with local G-CP-v iolation under global energy/information conservation. The two necessary conditions, however, can be used as an analytical basis for quantum submergence.
may also requires other conditions such as that both BQAs be involved in the same harmonic oscillations. Such harmonic oscillation is made possible with local G-CP-v iolation under global energy/information conservation. The two necessary conditions, however, can be used as an analytical basis for quantum submergence.
Theorem 11 (Information preservation principle). Quantum emergence and submergence entails the preservation of global G-CPT symmetry with or without local G-CP-violation.
Proof. It follows from that without global G-CPT symmetry there would be no bipolar dynamic equilibrium, no bipolar quantum agents (BQAs), no Yin and no Yang. ![]()
Theorem 12 (Information no-preservation principle). Quantum emergence and submergence cannot preserve background dependent information such as space and time.
Proof. It follows from that bipolar dynamic equilibrium entails G-CP-violation or equivalently G-T-violation which causes spacetime fluctuation. ![]()
Theorem 13 (Indeterminacy principle). If quantum coherence and decoherence or collapse are fundamentally quantum emergence and submergence under G-CPT symmetry, there would be no deterministic solution to the “measurement problem” in spacetime geometry; a relativistic and analytical approach to the problem in a background-independent geometry would be unavoidable.
Proof. It follows from Theorems 11 and 12. ![]()
Theorem 14. Since BQLA addition and multiplication operations can preserve G-CPT symmetry, G-CPT symmetry can be preserved in the emergence and submergence of a multiagent BQCA consisting of local or non-local background-independent BQAs with or without G-CP-violation using BQLA within BQG.
Proof. It follows from the proofs of Theorems 1 - 13. ![]()
Theorem 15 (Collective adaptation to global equilibrium under G-CPT Symmetry). Given
![]() with the two conditions of (1) "t, M(t) is energy-information conservational and (2) "t, the absolute values of the negative and positive energies of each row and each column of M are both greater than 0.0, without external disturbance, all bipolar elements in E connected and regulated by M will eventually reach a YinYang bipolar equilibrium or symmetry
with the two conditions of (1) "t, M(t) is energy-information conservational and (2) "t, the absolute values of the negative and positive energies of each row and each column of M are both greater than 0.0, without external disturbance, all bipolar elements in E connected and regulated by M will eventually reach a YinYang bipolar equilibrium or symmetry ![]() at certain time t, where
at certain time t, where ![]() is the total energy of E and K is the number of bipolar elements in E.
is the total energy of E and K is the number of bipolar elements in E.
Proof. It follows from that Condition (1) enables the energy of each element of E(t) be transmitted and distributed to E(t+1) in 100% with or without G-CP-violation; Condition (2) prevents the energy of E from bipolar oscillation toward a globally isotropic quantum world. Thus, the rebalancing process will continue indefinitely based on Equation (7a)-(7b) even after a dynamic bipolar equilibrium or symmetry is reached. ![]()
Based on Theorem 15, it can be concluded that, without bipolarity, there would be no G-CPT symmetry because: a) without bipolarity, there would be no charge parity and bipolar energy/information conservation as for Condition (1); b) without bipolarity, Condition (2) in Theorem 15 cannot be met.
With the discovery of CP-violation, CPT (Charge-Parity-Time) symmetry is now believed a fundamental law in physics (cf. [47] ), which explains why the universe exists as it is and why action-reaction and particle-anti- particle are almost always is an equilibrium or quasi-equilibrium. But the cause of this law has been a mystery. Law 9 can be deemed an equilibrium-based causation law of G-CPT symmetry with or without local G-CP-vi- olation. This is made possible by the scalable BQCA interpretation of quantum gravity in the background independent geometry.
Theorem 16 (Unification of CPT Symmetry and CP Violation). All symmetries in the universe are direct or indirect results of G-CPT symmetry. All violations of symmetry are direct or indirect results of G-CP-violation under the dynamic equilibrium of a global G-CPT symmetry..
Proof. Since weak and strong nuclear forces can be unified with electromagnetic force per Nobel Prizes in physics for 1979 and 2008 [48] [49] , electromagnetic and gravitational forces can be deemed the two basic forces and electromagnetic particle-antiparticle and gravitational action-reaction bipolarities can be regarded as the two basic bipolarities. The theorem follows from that G-CPT symmetry can unify electromagnetic particle- antiparticle and gravitational action-reaction bipolarities with or without G-CP-violations. ![]()
4. A Many-World Model of Quantum Emergence-Submergence for Causal Analysis of Quantum Coherence-Decoherence or Collapse
While bipolar quantum superposition and entanglement makes quantum emergence and submergence possible, with energy/information preservation the emergence and submergence makes it possible for different quantum worlds to come and go with G-CPT symmetry. For instance, a big bang leads to the emergence of a world and a black hole leads to the submergence of a world. Naturally, G-CPT symmetry subsumes an equilibrium-based many world model of quantum coherence and decoherence or collapse. The new approach is distinguished from other many-world or multiverse models by 1) its ubiquitous background-independent geometrical basis, 2) its bipolar dynamic logical basis and 3) its equilibrium-based unification of the many worlds into a single universe for geometrical, logical and causal analysis of quantum coherence and decoherence or collapse.
4.1. A 1-World Model
A 1-world BQG (1W-BQG) as a 2-dimensional space of YinYang bipolar complementarity is pivotal in hosting BDL, BQLA, and BQCA for BQA formation and multiagent BQA interaction in a dynamic equilibrium or non- equilibrium. While all agents in the universe can be deemed BQAs, how agents in the classical world interact with those in the quantum world is a mystery. For instance, the cause of decoherence and/or collapse by a measurement apparatus―a visiting BQA from the classical world-is geometrically and logically an unknown. We thus have the question: Can the background independent BQG be used to model BQA interactions between a classical and a quantum world?
Theorem 17. If BQAs in both the classical and the quantum worlds are all characterized as a bipolar dynamic equilibrium in bipolar scalar forms of (x,y) and (u,v), ![]() , BQG is theoretically adequate for modeling all background independent bipolar interactions among BQAs in the two worlds.
, BQG is theoretically adequate for modeling all background independent bipolar interactions among BQAs in the two worlds.
Proof. It follows from that, ![]() , the superposition, the multiplication, the entanglement, and all other bipolar operations between (x,y) and (u,v) must result in a bipolar value within BQG.
, the superposition, the multiplication, the entanglement, and all other bipolar operations between (x,y) and (u,v) must result in a bipolar value within BQG. ![]()
To illustrate we show in Figure 10 the submergence of a quantum superposition (x,y) to x and y in the classical world caused by a 3rd BQA―a negative disturbance from the classical world such as a measurement apparatus. Quantum submergence caused by a positive disturbance is would be a symmetrical case.
4.2. A 2-World Model
While BQG has been proven adequate for hosting BDL, BQLA, and BQCA for BQA formation and multiagent BQA interaction in dynamic equilibrium or non-equilibrium, the conversion of agents from the classical world to the quantum world is practically impossible in many cases. For instance, a quantum disturbance can be caused by
![]()
Figure 10. Submergence of superposition (x,y) to x and y in a 1W-BQG.
Definition 11. A 2-World BQG (2W-BQG) consists of two 2-D regions: 1) a bipolar equilibrium-based quantum world which forms the original BQG with a Yin dimension, a Yang dimension and a bipolar equilibrium dimension; 2) a truth-based classical word that includes all the remaining 2-D space beyond the quantum world.
Definition 12. A BQA within a quantum worldis called a normal BQA. A BQA within a classical worldis called an abnormal BQA. A BQA on the border line between the two worlds belongs to both worlds.
Theorem 18. Within the 2-world model, the superposition of two normal BQAs is always another normal BQA. The superposition of two abnormal BQAs can be normal or abnormal. The superposition of a normal BQA and an abnormal BQA can be normal or abnormal.
Proof. It follows from that,
1) Given two normal BQAs A = (x,y) and B = (u,v), the superposition ![]() must be within the quantum world of the 2W-BQG (see Figure 11(a)).
must be within the quantum world of the 2W-BQG (see Figure 11(a)).
2) Given a normal BQA A = (x,y) and an abnormal BQA B = (u,v), the superposition ![]() may be within the quantum or classical world (see Figure 11(b)).
may be within the quantum or classical world (see Figure 11(b)).
Given two abnormal BQAs A = (x,y) and B = (u,v), the superposition ![]() may be within the quantum or classical world (see Figure 11(b)).
may be within the quantum or classical world (see Figure 11(b)). ![]()
Theorem 19. Logically definable bipolar quantum entanglement is only valid among normal BQAs. An abnormal BQA in the classical world can be logically converted into a normal one for logically definable bipolar quantum entanglement.
Proof. It follows from that an agent in the classical world cannot be specified as a bipolar variable (x,y) such that "(x,y) Î B1, BF or B¥ until the agent is converted to a normal BQA. On the other hand, any agent is a BQA because any agent must be a collection of particles, antiparticles, or negative-positive energies which are inherently bipolar. ![]()
Recall that, BQG is for bipolar interaction and bipolar dynamic equilibrium analysis. It is quadrant irrelevant. Superposition results from bipolar interaction which transcends spacetime and thus can be represented with scalar values. From the above theorem, it is clear that 2W-BQG may play an important role in the analysis of bipolar quantum disturbance, decoherence and collapse. It makes it possible to integrate BQAs from different worlds and to picture quantum disturbances caused by visiting abnormal BQAs. Most interestingly, the observation that the superposition of two abnormal BQAs may be normal provides an important lead for research and development of symmetrical quantum measurement technologies for zero-disturbance or reduced level of decoherence of quantum entanglement.
![]()
Figure 11. 2W-BQG and multiagent interaction of classical and quantum worlds.
While Shrödingier’s equation is fully deterministic and the only place where determinism is lost in the context of quantum mechanics is at the point of a measurement, G-CP-violation under G-CPT symmetry presents a fundamental departure from Shrödingier’s deterministic wave function through the incorporation of gravitation into G-CP-violation under G-CPT symmetry―a quantum gravity theory with logically definable causality.
Theorem 20. Submergence of a quantum entanglement can be caused by G-CP-violation under G-CPT symmetry.
Proof. If any gravitational or electromagnetic disturbance associated with a quantum measurement causes additional local G-CP-violation of a two-party entanglement, the conditions for coherence in Theorem 15 can be violated to result in submergence of the entanglement while global G-CPT symmetry is preserved. Thus, the theorem follows from the two conditions of Theorem 15 and last theorem. ![]()
Quantum emergence and submergence theory leads to a unification of coherence, decoherence and collapse theories. Figure 12(a) depicts the unification where decoherence is characterized as fundamentally the loss of local equilibrium and harmony due to due to G-CP-violation caused by disturbance, where collapse is characterized as fundamentally submerging from YinYang bipolar quantum superposition to the Yin and Yang in the classical world. Figure 12(b) depicts submergence due to G-CP-violation caused by an opposite disturbance. Figure 12(c) depicts submergence due G-CP-violation caused a positive disturbance.
With the emergence-submergence theory, the “measurement problem” becomes a logically comprehensible problem.
1) Quantum superposition can be logically and mathematically characterized as an emergence of YinYang bipolar equilibrium of two BQAs A = (x,0) and B = (0,y) of a 2W-BQG and we have,
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 12. Unification of quantum coherence and decoherence or collapse with emergence-submergence: (a) Submergence due to G-CP-violation caused by a negative disturbance; (b) Submergence due to G-CP-violation caused by a opposite disturbance; (c) Submergence due to G-CP-violation caused by positive a disturbance.
![]() (11a)
(11a)
Based on Equation (8a), the emergence can be logically defined as an energy/information conservational operation with a bipolar quantum logic gate matrix.
![]() . (11b)
. (11b)
The nature of quantum decoherence and collapse can be logically and mathematically characterized as quantum submergence (ß) or the loss of a 2-party bipolar equilibrium without losing the two BQAs, where
![]() (11c)
(11c)
The separation of (x,y) can also be defined as the reverse of Equation (11b) with energy/information conservation.
![]() . (11d)
. (11d)
In Equation (11d), ![]() is a new operator that replace × with & without changing the rule of matrix multiplication. In the result bipolar matrix, (0,0) can characterize the collapse of (x,y) from one world to another and
is a new operator that replace × with & without changing the rule of matrix multiplication. In the result bipolar matrix, (0,0) can characterize the collapse of (x,y) from one world to another and ![]() can characterize the returning of the BQAs A and B to a world after decoherence due to quantum disturbance.
can characterize the returning of the BQAs A and B to a world after decoherence due to quantum disturbance.
2) Quantum decoherence can also be logically and mathematically characterized as the loss of the bipolar equilibrium of a nonlocal 2-party BQA entanglement due to disturbance that caused the submergence or returning of the two BQAs to a world as separate agents. If we use the submergence or decoherence operator ß as the reverse of a superposition or entanglement (W), a submergence of a bipolar entanglement can be logically described as a causal relation as proven in Theorem 15 with different cases. Formally, given ![]() ;
;![]() ;
; ![]() or
or ![]() , we have, "t,i,j,
, we have, "t,i,j,
Case 1:![]() (11c)
(11c)
Case 2:![]() (11d)
(11d)
4.3. A 3-World Model
The 2-world model can be extended to a three world BQG (3W-BQG) model as shown in Figure 13. In this model any two BQGs can be separated by a classical world. Since the two BQGs can be identical, one can be used as a cache memory of the other. It can also be used for non-local entanglement of two BQAs or BQCAs separated by a distance. This is not further discussed.
4.4. A 4-World Model
While the 3W-BQG shows the advantage of bipolar equivalence, it lacks bipolar symmetry. This deficiency can be remedied with a 4-world model.
Definition 13. A 4-World BQG (4W-BQG) has two symmetrical quantum worlds and two symmetrical classical worlds. The two quantum worlds are two symmetrical BQGs jointed at (0,0) and the joint creates the two symmetrical classical worlds at the same time, one is a positive world and the other a negative one (see Figure 14).
The 4-world model might be seen as merely a 2-D Cartesian coordinate or analytical geometry with four quadrants, but it is not. First the coordinate is not an X-Y coordinate but a YinYang bipolar coordinate. The quantum worlds are bipolar equilibrium-based and background-independent, that means the four worlds can be rotated or flipped as needed as long as the symmetries are preserved. Thus, the 4-world model is essentially different from
analytical geometry, one hosts equilibrium-based BDL, BQLA, BQAs and BQCAs; another hosts truth-based BL, LA, classical world agents and truth-based cellular automatons which can be background dependent.
In the 4-world model, local quantum superposition and entanglement can be positioned in one quantum world; non-local quantum superposition and entanglement can cross two symmetrical quantum worlds. One classical world provides a region for positive disturbances and another for negative disturbance. Figure 15(a) shows that two quantum agents (x,y) and −(x,y) emerged in an entanglement and submerged due to a negative disturbance. Figure 15(b) shows the submergence as the loss of coordination of two regulatory quantum gate matrices. The asymmetrical disturbance can be associated with the apparatus of a quantum measurement.
Different from other models, within the 4-world model, the superposition of any two BQAs can be normal or abnormal unless both of them are within the same world. Sincenothing “cancels” gravity because it is only attractive unless a symmetrical gravitational source is created, the 4-world model is interesting due to its symmetrical property for bipolar quantum entanglement and its potential for developing symmetrical measurement technologies such that the gravitational effects of two symmetrical measurement apparatus can be cancelled. Figure 15(c) shows a 1-dimensional cancellation.
Theorem 21. Decoherence of a bipolar quantum entanglement can, theoretically, be minimized or prevented by applying symmetrical measurement.
Proof. It follows from that symmetrical measurement from all sides of an entanglement at the same time causes symmetrical disturbances that cancel each other and logically maintain the coherence of the bipolar quantum entanglement. ![]()
4.5. A Many-World Model
From the early sections, we see that
1) The 1W-BQG shows the advantage of complete background independence;
2) The 2W-BQG shows the advantage of quantum word and classical world interaction;
3) The 3W-BQG shows the advantage of non-local quantum equivalence;
4) The 4W-BQG shows the advantage of quantum symmetry.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 15. A 4-world interpretation: (a) Submergence of a 2-party entanglement caused by a negative disturbance; (b) Submergence as loss of coordination of two regulatory matrices; (c) Symmetrical measurement at the same time to reduce or prevent submergence.
While the four world models show some different properties, the ubiquitous nature of YinYang bipolarity makes BQG ubiquitous―a property of background independence. Thus, BQG can be anywhere. That means, the 1W-, 2W-, 3W- and 4W-BQG models can be combined in any configuration for different applications. This leads to a many world model of BQG. This is not further discussed in this work.
5. Discussion and Predictions
5.1. Physics as a Logical System of Thought
Einstein asserted [50] : “Physics constitutes a logical system of thought which is in a state of evolution, whose basis (principles) cannot be distilled, as it were, from experience by an inductive method, but can only be arrived at by free invention.” He affirmed [51] : “Pure thought can grasp reality” and “Nature is the realization of the simplest conceivable mathematical ideas.” He reasserted [52] : “For the time being we have to admit that we do not possess any general theoretical basis for physics which can be regarded as its logical foundation.”
In light of the above, BQG and BDL has been proposed as an equilibrium-based geometrical and logical foundation for quantum mechanics and quantum gravity with an equilibrium-based interpretation of energy/information, quantum superposition and entanglement. Although it is questionable whether the equilibrium- based geometrical and logical system is what Einstein sought for physics in the last century, BQG has been proven completely background independent and BDL has been proven a bipolar dynamic generalization of Boolean logic (BL). BDL does satisfy the simplicity criterion set forth by Einstein and has passed a major falsifiability test with a logical exposition of the longstanding puzzle of Dirac 3-polarizer experiment.
While background independent geometry has been advocated by Lee Smolin in the quest for quantum gravity [27] , no formal logical system has been reported for completely background independent geometrical reasoning with logically definable causality besides BDL. A distinguishing factor lies in YinYang bipolar complementarity. No matter time is real or unreal, fundamentally different from the Yin and the Yang of Nature, space and time are not bipolar interactive and cannot form bipolar dynamic equilibrium, symmetry, quantum superposition and entanglement. This could be the reason why other approaches to quantum gravity so far stopped short in finding a unique logical foundation as a general theoretical basis for physics.
Now, BDL and BQLA have led to an equilibrium-based bipolar quantum cellular automaton (BQCA) interpretation of quantum mechanics and quantum gravity. Not only has BQCA logically unified matter and antimatter atoms, it also has led to a cellular model for quantum emergence and submergence. While alternative interpretations of quantum mechanics all have led, in practice, to exactly the same answers and predictions regarding the observations, fundamentally different from others the equilibrium-based interpretation claims thatspace- time, particle-wave and imaginary-real are not most fundamental complementarities and therefore quantum mechanics in Hilbert space cannot be most fundamental, albeit practically useful.
It is observed that missing in the Hamiltonian, Schrödinger’s wave function, Hilbert space, Dirac bra-ket notation, complex numbers, qubits, and quantum logic gates is the common property of bipolar complementarity. While Schrödinger’s wave function is deterministic and does not account for bipolar coexistence, BDL and BQLA provide explicit bipolar representation. While alternative interpretations of quantum mechanics so far failed to deviate themselves from quantum mechanics in a fundamental way, bipolar quantum superposition and entanglement present a fundamental departure from the established theories. A key property of this departure is the background independent bipolar property of BQG that makes BDL and BQLA transcendent over spacetime and particle-wave. With this transcendence, quantum decoherence or collapse can be interpreted as quantum submergence of a superposition―a reverse process of quantum emergence with logically definable causality for an analytical paradigm.
5.2. Unification of Quantum Locality and Non-Locality
Quantum entanglement or quantum non-locality as an unresolved illogical paradox has generated enormous amount of confusion. It was once called “spooky action at a distance” by Einstein. The background-independent multiagent BQCA approach provides an equilibrium-based causal logic interpretation to the paradox and lead to the following predictions (adapted from [16] - [26] ).
Prediction 1. Quantum entanglement can be classified as local or non-local and strong or weak. A local entanglement is a strong one with a nucleus as a local regulatory center; a non-local entanglement is a weak one without a local regulatory center. Any local entanglement as a local dynamic equilibrium must exists in a global entanglement or equilibrium.
Prediction 2. Matter or antimatter atom is logically a set of n-party locally entangled electron-positron pairs through a bipolar quantum logic gate characterizing the nucleus―an organizational or regulatory center of the atom under G-CPT symmetry.
Prediction 3. A composite quantum agent with two or more non-local quantum agents can be deemed an n-party non-local entanglement.
Prediction 4. Any composite quantum agent in the universe including the universe itself is a combination of local and non-local quantum entanglements.
Prediction 5. Every composite BQA in the universe including the universe itself is a BQCA.
The unification of quantum locality and non-locality provides a basis for quantum biology, mind-body unification and quantum intelligence. Evidently, a background independent geometry with spacetime transcendence is essential for logically definable quantum causality as well as local and non-local quantum entanglements.
A letter from Einstein to R. A. Thornton dated Dec. 7, 1944 wrote [cf. [53] , p. 310-311]: I fully agree with you about the significance and educational value of methodology as well as history and philosophy of science. So many people today―and even professional scientists―seem to me like someone who has seen thousands of trees but has never seen a forest. A knowledge of the historical and philosophical background gives that kind of independence from prejudices of his generation from which most scientists are suffering. This independence created by philosophical insights is-in my opinion- the mark of distinction between a mere artisan or specialist and a real seeker after truth.
Could most scientists of this generation be suffering from the lack of that kind of independence from prejudices? G-CPT symmetry leads to the following predictions (adapted from [16] - [26] ):
Prediction 6. Quantum superposition and entanglement is fundamentally a bipolar dynamic equilibrium or harmony that can emerge from the bipolar interaction of Nature’s Yin and Yang and submerge to the Yin and Yang with global energy/information conservation.
Prediction 7. Any valid and fundamental departure from quantum mechanics must be able to 1) provide a logical definition of quantum entanglement, 2) provide a logical unification of energy and information, and 3) provide a logical exposition of Dirac 3-polarizer experiment. Otherwise, it is either invalid or non-fundamental.
Prediction 8. Quantum coherence is fundamentally the emergence of a local BQCA of n-party (2 < n <¥) quantum superposition or entanglement (coupled) into a global BQCA of ¥-party superposition and/or entanglement. Quantum decoherence or collapse is fundamentally quantum submergence of a local BQCA decoupled from a global BQCA back to the classical world.
Prediction 9. Quantum uncertainty in general is due to 1) the less fundamental nature of Bohr’s particle-wave complementarity compared with YinYang bipolar complementarity, 2) the less fundamental nature of spacetime or Hilbert space compared with YinYang bipolar quantum geometry, 3) the less fundamental nature of quantum superposition compared with bipolar quantum superposition, 4) the less fundamental nature of CPT symmetry compared with G-CPT symmetry, and 5) the less fundamental nature of truth compared with bipolar dynamic equilibrium.
Prediction 10. The fact that different interpretations of quantum mechanics all lead, in practice, to exactly the same answers and predictions regarding the observations is due to the lack of holistic observations of YinYang bipolar coexistence in dynamic equilibrium which is required for resolving the problem of decoherence and/or collapse associated with “the measurement” problem.
Prediction 11. A valid and fundamental departure from Schrödinger’s deterministic wave function entails a bipolar dynamic equilibrium-based quantum gravity unification of particle-antiparticle bipolarity and gravitational action-reaction bipolarity. Without such a unification, a valid interpretation of quantum mechanics cannot be a fundamental departure from Shrödingier’s deterministic wave function.
Prediction 13. All logical, physical, social, biological and mental regeneration and degeneration are fundamentally quantum emergence and submergence, respectively, and all worlds are bipolar quantum entangled under G-CPT symmetry. Thus, a valid quantum gravity theory must be a unifying theory of logical, physical, social, biological, and mental quantum gravity with information conservation.
Quantum emergence and submergence under G-CPT symmetry provides a theoretical basis for the unification of big bang and black hole theories with information conservation.
Prediction 14. Big bang is a process of quantum emergence from a quantum world to a classical world; black hole is a process of quantum submergence from a classical world to a quantum world.
Prediction 15. No world can be completely separated from other worlds; all classical and quantum worlds must be unified under the global dynamic equilibrium of G-CPT symmetry.
Prediction 16. A possible solution to quantum decoherence or collapse associated with the “measurement problem” is to develop bipolar symmetrical quantum registers and bipolar symmetrical measurement technologies that can reduce or prevent quantum submergence.
It should be remarked that, the fact that researchers were able to reduce environmental decoherence rate “to levels far below the threshold necessary for quantum information processing” by applying high magnetic fields in their experiment [14] can be deemed supporting evidence for Prediction 16.
Prediction 17. A fundamental departure from quantum mechanics is more likely to appear in a less established journal than in an established one due to the strong establishment of classical logical thinking in established scientific fields and their lack of the kind of independence from prejudices from which most scientists of this generation are suffering.
Prediction 18. Truth-based logic is human logic; equilibrium-based logic is God (or Nature) logic. Mankind has been using human logic for thousands of years in seeking truths from the universe. Now, it is time for mankind to seek and accept God logic as a guiding light for scientific and technological endeavors.
6. Conclusions
Fundamentally different from established quantum mechanical and quantum gravity theories, the new theory is backed by a completely background independent holistic formal logical, geometrical, and algebraic system. This distinction has been shown essential for modeling the quantum world as a multiagent environment with logically definable quantum causality for causal analysis of quantum coherence, decoherence and collapse under G-CPT symmetry with or without G-CP-violation.
While this work has been focused on logically definable causal analysis, it can be further developed from a logical foundation to a physical one with future research efforts. The potential is backed with a number of vindications including:
1) While mainstream science is based on truth and singularity in which time starts with big bang and ends with black hole, dynamic equilibrium is based on bipolarity of input-output or negative-positive energies. However, the theory of truth and singularity is not a contradiction but a vindication of bipolarity because the bipolar property of nature’s basic forces and particles are the only properties that can survive a big bang as well as a black hole due to particle-antiparticle emission [60] [61] .
2) The new interpretation is based on an equilibrium-based logical extension of Niels Bohr’s particle-wave interpretation of YinYang duality to electromagnetic particle-antiparticle and gravitational action-reaction bipolar complementarity. Bipolar complementarity has led to the unification of energy and information.
3) Bipolar complementarity has resulted in BDL―a sound and formal generalization of Boolean logic from bivalent truth domain to bipolar equilibrium-domain. With the first logical exposition of Dirac 3-polarizer experiment, BDL has been vindicated as a valid causal logic that leads to the unification of mind, light and matter [26] .
4) Without YinYang bipolarity, logically definable causality would be impossible [21] .
5) BDL has led to BQLA―a bipolar quantum linear algebra that has been shown preserving quantum superposition amplitude and enables energy-information conservation, regeneration and degeneration of a BQCA for global regulation.
6) BDL and BQLA have made it possible to define both local and non-local bipolar quantum superposition and entanglement as multiagent BQCAs for unified logical analysis of quantum emergence, submergence, decoherence and collapse.
7) The background independent property of BQG has led to the unification of classical and quantum worlds into a many-world model.
8) Multiagent BQCAs have led to a geometrical and logical quantum gravity theory where electromagnetic and gravitational disturbance can be accounted for as G-CP-violations under G-CPT symmetry.
Finally, G-CPT symmetry has led to a number of philosophical, logical and technical predictions. Unlike string theory where strings or monopoles are imaginable but untestable, dipoles and bipolarity as a basis for the new theory are observable everywhere. Thus, G-CPT symmetry exhibits the necessary falsifiability for a scientific theory and the predictions are expected to be testable in the future. After all, as an equilibrium-based logical theory G-CPT symmetry will, hopefully, lead to analytical and physical solutions to the quantum disturbance problem associated with the “measurement problem” and serve as a point of fundamental departure from the crossroad of theoretical physics but not as “what goes around comes around” .
Acknowledgements
This paper was reviewed and accepted for publication by Journal of Modern Physics (JMP). It was transferred to JQIS on the author’s request. The author acknowledges the JMP anonymous reviewers for their helpful comments and suggestions.
Appendix. Bipolar Dynamic Logic (BDL)
(Adapted from [16] )
Appendix 1: Figures A1-A4 show a world of bipolar sets, bipolar lattices, and bipolar interactions. Table A1 provides the basic operations of BDL each of which can be a cause for an effect. The laws in Table A2 hold on BDL. Bipolar universal modus ponens (BUMP) is listed in Table A3 which formally defines equilibrium-based bipolar causality as an inference rule and leads to generic bipolar quantum entanglement. The zero order BDL has been extended to a 1st order formal system (Zhang 2011 Ch3) in which equilibrium-based bipolar predicates can be used similarly as truth-based predicates. For instance, given bipolar agent A and let the bipolar functor (f−,f+) be self-negation and self-assertion abilities, (f−,f+)(A) can denote the mental equilibrium or non-equilibrium of A; given bipolar agents A and B and let the bipolar functor (r−,r+) be competition and cooperation relations, (r−,r+)(A,B) can denote the relation between A and B.
An equilibrium-based axiomatization is shown in Table A4 which has been proven sound (Zhang 2011 Ch.3). In BDL Å and Å− are “balancers” that can, at the most basic level, be used as nuclear (or mental) fusion operators; Æ, Ä, Æ− and Ä− are intuitive and counter-intuitive “oscillators” that leads to particle wave unification; & and &- are “minimizers” that can, at the most basic level, be used as particle-antiparticle annihilation operators.
![]()
Figure A1. Hasse diagram of bipolar (quantum) lattice B1 in bipolar geometry (Zhang & Zhang 2004).
![]()
Figure A2. Hasse diagram of bipolar (quantum) fuzzy lattice BF (Zhang 2005).
![]()
Figure A3. Hasse diagram of bipolar algebraic quantum lattice B∞.
![]()
Figure A4. Bipolar relativity: Non-reciprocal bipolar interaction; (b) Reciprocal bipolar interaction; (d) Oscillation; (e) Bipolar entanglement (Zhang 2011).
![]()
Table A1. Operations of bipolar dynamic Logic (BDL) ("(x,y),(u,v)ÎB1, Equations (1)- (12) define BDL. |x| is used for explicit bipolarity).
![]()
Table A2. Laws of bipolar equilibrium/non-equilibrium.
![]()
Table A3. Bipolar Universal Modus Ponens (BUMP).
§ Bipolar conjunction: e.g.![]() ; or
; or ![]() , which provides a logical exposition to how a single photon gets through Dirac’s 3-polarizers―a mystery for almost a century (Zhang and Marchetti, 2015a-c).
, which provides a logical exposition to how a single photon gets through Dirac’s 3-polarizers―a mystery for almost a century (Zhang and Marchetti, 2015a-c).
§ Bipolar fusion, disjunction or quantum superposition: e.g.![]() , where (−1, +1) can represent a harmonic competition-cooperation relation or a mental equilibrium/harmony. Such bipolar coexistence is impossible with truth-based logic. On the other hand, YinYang bipolar coexistence in equilibrium and harmony such as input-output balance has nothing contradictory.
, where (−1, +1) can represent a harmonic competition-cooperation relation or a mental equilibrium/harmony. Such bipolar coexistence is impossible with truth-based logic. On the other hand, YinYang bipolar coexistence in equilibrium and harmony such as input-output balance has nothing contradictory.
§ Bipolar annihilation, minimization, or conjunction: e.g.![]() , where two opposites are annihilated;
, where two opposites are annihilated;![]() , where (x,y) is minimized.
, where (x,y) is minimized.
§ Bipolar interaction and oscillation: e.g.![]() , where (−1,0)n is an oscillation sequence of the Yin and the Yang; when n is even,
, where (−1,0)n is an oscillation sequence of the Yin and the Yang; when n is even,![]() ; when n is odd,
; when n is odd,![]() .
.![]() , where (x,y) is destroyed or nullified.
, where (x,y) is destroyed or nullified.
§ Bipolar fission: e.g. fission![]() , where
, where ![]() can characterize a nuclear fission, a mental or organizational separation from equilibrium and harmony to mixed depression and mania.
can characterize a nuclear fission, a mental or organizational separation from equilibrium and harmony to mixed depression and mania.
![]()
Table A4. Proven sound equilibrium-based vs. Truth-based axiomatization.
As a causal set, a bipolar relational matrix R is characterized with bipolar logical values such as (0,0) for no relation, (−1,0) or (−0.8,0) for conflict relation, (0,+1) or (0,+0.7) for coalition, and (−1,+1) or (−0.9,+0.9) for harmonic relation, respectively, with different crisp or fuzzy strengths. The Å-Ä bipolar transitive closure of R is the smallest bipolar transitive relation containing R (Zhang & Zhang, 2004) denoted by  and
![]() (A1)
(A1)
It has been proven that, let ![]() be a finite bipolar set, the Å-Ä bipolar transitive closure  of R in X exists, is unique,
be a finite bipolar set, the Å-Ä bipolar transitive closure  of R in X exists, is unique,
![]() (A2)
(A2)