Non-Perturbative Analysis of Various Mass Generation by Gluonic Dressing Effect with the Schwinger-Dyson Formalism in QCD ()
Received 15 February 2016; accepted 26 April 2016; published 29 April 2016

1. Introduction
Quantum chromodynamics (QCD) is the fundamental gauge theory of the strong interaction, and it is a long important problem to describe hadron structure and properties based on QCD. Quarks and gluons, the basic ingredients of QCD, strongly interact with each other in an infrared region, and they are confined in hadrons. Then, due to their non-perturbative properties, it is fairly difficult to describe hadrons directly from QCD. Also, the non-perturbative dynamics in QCD directly relates to the other important physical subject of “mass generation.”
The origin of mass is one of the most fundamental issues in physics. One famous category of mass generation is the Yukawa interaction with the Higgs field. However, even besides the dark sector, the Higgs-origin mass is only about 1% of the total mass in our universe, where dominant massive particles are nuclei (u,d quarks) and electrons. Actually, the Higgs interaction only gives the electron mass (about 0.5MeV) and a small current quark mass (a few MeV) for u,d quarks [1] . In contrast, about 99% of mass of matter in our universe are created by the
strong interaction, apart from the dark sector. In fact, a large constituent quark mass of  arises from non-perturbative dynamics in QCD. Thus, QCD gives another category of mass generation.
arises from non-perturbative dynamics in QCD. Thus, QCD gives another category of mass generation.
Such a dynamical fermion-mass generation in the strong interaction was first pointed out by Y. Nambu et al. [2] in 1961 in the context of spontaneous chiral-symmetry breaking. The QCD-based quantitative analysis of dynamical fermion mass generation was performed by Higashijima and Miransky in 1980’s [3] [4] using the Schwinger-Dyson formalism. Thus, light u,d-quarks are considered to acquire a large constituent quark mass of about 300 - 400 MeV, in accordance with spontaneous chiral-symmetry breaking.
Even without chiral symmetry breaking, however, it is likely that QCD has several dynamical mass generation mechanism. For example, while the charm quark has no chiral symmetry, some difference seems to
appear between current and constituent masses for charm quarks: the current mass is 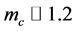 GeV at renor- malization point
GeV at renor- malization point 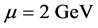 [1] , and the constituent charm quark mass is
[1] , and the constituent charm quark mass is  in the quark model.
in the quark model.
The gluon is more drastic case. While the gluon mass is zero in perturbation QCD, the non-perturbative effect of the self-interaction of gluons seems to generate a large effective mass of 0.6 GeV [5] - [7] , and the lowest glueball mass is about 1.6GeV [8] [9] . Furthermore, the dynamical mass generation for scalar-quark have been studied in the lattice scalar-QCD calculation [10] . Thus, we deduce that “quantum color dynamics” generally accompanies a large mass generation, due to the strong interaction.
Next, let us consider compositeness of hadrons in terms of quarks. As an infrared effective theory, the constituent quark model has been successful for the description of the hadron spectroscopy. The constituent
quark belongs to the fundamental representation 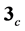 in the
in the 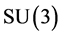 color group, and many hadrons can be
color group, and many hadrons can be
classified as the color-singlet ( ) bound states of some quarks and antiquarks. In this picture, ordinary mesons and baryons are identified as quark-antiquark and three-quark systems, respectively. However, besides the ordinary baryons and mesons, QCD allows the existence of other color-singlet states, such as glueballs, hybrids and multi-quark states, called exotic hadrons. Recent experiments have reported the candidates for these exotic states [1] . The heavy hadrons, which includes one or more heavy (anti)quarks, are also recent hot topics in hadron physics [1] [11] [12] . For example, very recently, LHCb has reported the discovery of two charmed pentaquarks,
) bound states of some quarks and antiquarks. In this picture, ordinary mesons and baryons are identified as quark-antiquark and three-quark systems, respectively. However, besides the ordinary baryons and mesons, QCD allows the existence of other color-singlet states, such as glueballs, hybrids and multi-quark states, called exotic hadrons. Recent experiments have reported the candidates for these exotic states [1] . The heavy hadrons, which includes one or more heavy (anti)quarks, are also recent hot topics in hadron physics [1] [11] [12] . For example, very recently, LHCb has reported the discovery of two charmed pentaquarks, 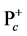 (4380) and
(4380) and  (4450), from a careful analysis of the decay product in the high-energy process, and this report seems to activate the multi-quark physics again [13] .
(4450), from a careful analysis of the decay product in the high-energy process, and this report seems to activate the multi-quark physics again [13] .
In the theoretical study of these states, the diquark picture [14] [15] has been discussed as an important effective degree of freedom. The diquark is composed of two quarks with strong correlation, where the
one-gluon-exchange interaction between two quarks is attractive in the color anti-triplet 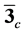 channel [16] [17] , of which color is the same as an anti-quark. In
channel [16] [17] , of which color is the same as an anti-quark. In  flavor case, the flavor-antisymmetric and spin-singlet
flavor case, the flavor-antisymmetric and spin-singlet
with even parity is the most attractive channel in diquark, which is called scalar diquark. If the diquark correlation is developed in a hadron, this scalar diquark channel would be favored. The diquark correlation in a hadron is discussed in various situations, such as tetra-quarks, heavy baryons and other exotic states [18] [19] . The tetra-quark states as the bound state of the diquark/antidiquark is suggested in early day [20] , and X(3872) [21] and X(1576) [22] are considered as tetra-quark states. Light flavor mesons as tetra-quark [23] - [32] and mixing with 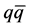 state [33] - [35] are discussed. There are various studies the heavy baryons focused on diquark [36] - [40] , e.g., single heavy quark/light diquark (
state [33] - [35] are discussed. There are various studies the heavy baryons focused on diquark [36] - [40] , e.g., single heavy quark/light diquark (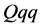 ) picture [41] - [45] . The other exotic states including heavy quark(s) are studied [46] - [52] . The ordinary baryon properties focused on the diquarks have been also discussed [53] - [57] . The diquark correlation is found in the lattice QCD simulation [58] - [61] . It is also considered that the diquark condensation is occurred in an extremely high density system, called the color superconductivity [62] . We note that diquark properties strongly depend on the color number
) picture [41] - [45] . The other exotic states including heavy quark(s) are studied [46] - [52] . The ordinary baryon properties focused on the diquarks have been also discussed [53] - [57] . The diquark correlation is found in the lattice QCD simulation [58] - [61] . It is also considered that the diquark condensation is occurred in an extremely high density system, called the color superconductivity [62] . We note that diquark properties strongly depend on the color number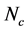 . If we consider the two-color QCD, the diquarks compose the color singlet (baryons). The strength of correlation between two quarks is same as quark/antiquark channel, and the (diquark-)baryons correspond to the mesons. This fact is known as the Pauli-
. If we consider the two-color QCD, the diquarks compose the color singlet (baryons). The strength of correlation between two quarks is same as quark/antiquark channel, and the (diquark-)baryons correspond to the mesons. This fact is known as the Pauli-
Gürsey symmetry. The quark-hadron matter in two-color system is investigated [63] - [69] . For the 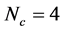 case, the diquarks belong to
case, the diquarks belong to ![]() or
or![]() . As an interesting fact for the case, the diquark contents must be different between baryons and tetra-quarks. In fact, the diquark
. As an interesting fact for the case, the diquark contents must be different between baryons and tetra-quarks. In fact, the diquark ![]() in an
in an ![]() baryon
baryon ![]() belongs to
belongs to![]() , which is self-adjoint. On the other hand, the diquark in a tetra-quark
, which is self-adjoint. On the other hand, the diquark in a tetra-quark ![]() belongs to
belongs to![]() . From this viewpoint, the
. From this viewpoint, the ![]() case is rather special, because the diquarks belong to the same color
case is rather special, because the diquarks belong to the same color ![]() in both cases of baryon
in both cases of baryon ![]() and tetra-quark
and tetra-quark![]() .
.
The properties of diquarks such as the mass and size are not understood well, although the diquarks have been discussed as important object of hadron physics. While the diquark is made by two quarks with gluonic interaction, it still strongly interacts with gluons additionally because of its non-zero color charge. Therefore, such dressing effect of gluons for diquark should be considered in a non-perturbative way. The dynamics of diquark and gluons may affect the structure of hadrons. In the quark-hadron physics, the Schwinger-Dyson (SD) formalism is often used to evaluate the non-perturbative effect based on QCD [3] [4] [70] - [78] . In this paper, we apply the SD formalism to scalar diquark to investigate the effective mass of scalar diquark, which reflects a non-perturbative dressing effect by gluons. The scalar diquark is treated as an extended field like a meson in effective hadron models, and interacts with the gluons [10] [42] .
For the argument of the scalar diquark, it would be important to consider its effective size. For, point scalar particles generally have large radiative corrections even in the perturbation theory [79] [80] . As an example, in the framework of the grand unified theory (GUT), the Higgs scalar field suffers from a large radiative correction of the GUT energy scale, and therefore severe “fine-tuning” is inevitably required to realize the low-lying Higgs mass of about 126 GeV [81] , which leads to the notorious hierarchy problem [79] [80] . The Higgs propagator with radiative correction has been investigated by setting the mass renormalization condition to reproduce 126 GeV [82] - [84] . A similar large radiative correction also appears for point-like scalar-quarks, which correspond to compact scalar diquarks, in scalar lattice QCD calculations [10] . In fact, the point-like scalar-quark
interacting with gluons acquires a large extra mass of about 1.5 GeV at the cutoff![]() , where a is the
, where a is the
lattice spacing. Such a large-mass acquirement would be problematic in describing hadrons with scalar diquarks. However, since it is a bound-state-like object inside a hadron, the diquark must have an effective size. This effect gives a natural UV cutoff of the theory, and reduces the large radiative correction. Then, we take account of the effective size and investigate the mass of the scalar diquark inside a hadron within the SD formalism.
This paper is organized as follows. In Section 2, we review the SD formalism for the light quark, as the typical fermion mass generation in QCD. In Section 3, we investigate the SD equation for the scalar diquark, where a simple form factor is introduced for the possible size of diquark. In Section 4, we present the numerical result of the diquark self-energy with the dependence of the bare mass and size of diquark, and briefly discuss the dynamical mass generation for the scalar diquark in the SD formalism. Section 5 is devoted to conclusion and discussion.
2. Dynamical Mass Generation of Quarks in QCD
The chiral symmetry is a fundamental symmetry in the light-quark sector of QCD, and it is an exact global symmetry in the chiral limit. In the low-energy region of QCD, spontaneous chiral-symmetry breaking takes place, which generates a large effective mass of light quarks. Actually, in the theoretical analysis with the Schwinger-Dyson (SD) formalism in QCD, a large self-energy generation of quarks is demonstrated in an infrared region, which breaks the chiral symmetry in the physically stable vacuum [3] [4] . In this section, as the standard fermionic mass generation in QCD, we briefly review the quark mass generation in the SD formalism for QCD in the Landau gauge, which is frequently used. This review part gives a important basis for the non-perturbative QCD physics, and is also useful to set up the formalism for the scalar diquark case in Section 3.
As a merit of the Lorentz-covariant gauge like the Landau gauge, the dressed quark propagator is generally described as ![]() with the wave function renormalization
with the wave function renormalization ![]() and the self-energy of quark
and the self-energy of quark![]() . The general and exact SD equation for the quark propagation is diagrammatically
. The general and exact SD equation for the quark propagation is diagrammatically
expressed in Figure 1. In principle, the quark propagator is exactly obtained by solving this equation, if the exact form of the gluon propagator and the quark-gluon vertex are given. Here, the kernel in the SD equation
depicted in Figure 1 is expressed by the product of the quark-gluon vertex ![]() and the gluon dressing function
and the gluon dressing function ![]() [85] ,
[85] ,
![]() (1)
(1)
where ![]() (
(![]() ) denotes the generator of the SU(Nc) color group.
) denotes the generator of the SU(Nc) color group.
In the most SD studies for quarks, one takes the rainbow-ladder approximation with the renormalization- group improvement of the quark-gluon vertex at the one-loop level. Note that, owing to the iterative structure of the SD equation, a simplified full-order treatment on the coupling ![]() can be achieved, even with the use of the one-loop level vertex and so on. In actual, by the diagrammatical expansion, one can easily confirm the inclusion of infinite order of the coupling
can be achieved, even with the use of the one-loop level vertex and so on. In actual, by the diagrammatical expansion, one can easily confirm the inclusion of infinite order of the coupling![]() , and the non-perturbative effect of gluons is thus included in this formalism. Recall that any nontrivial vacuum cannot be expressed by the perturbation theory.
, and the non-perturbative effect of gluons is thus included in this formalism. Recall that any nontrivial vacuum cannot be expressed by the perturbation theory.
Here, we briefly mention the treatment of quark confinement in the SD approach. In most works of the SD approach, the confinement effect is ignored, which seems problematic for the study of QCD. On this point, several recent studies, both analytical works [86] and lattice QCD simulations [87] , have suggested that chiral symmetry breaking and quark confinement are not directly correlated in QCD. If this is the case, even without confinement, one may be able to discuss chiral symmetry breaking in QCD, as is the SD approach.
At the one-loop level of renormalization-group improvement, the SD kernel is approximated as
![]() (2)
(2)
and the Landau-gauge gluon propagator is given as
![]() (3)
(3)
Then, by taking Dirac trace or the trace after multiplying![]() , the SD equation for the quark is expressed by the coupled integral equations:
, the SD equation for the quark is expressed by the coupled integral equations:
![]() (4)
(4)
![]() (5)
(5)
with the bare quark mass ![]() and the Casimir operator
and the Casimir operator ![]() in the SU(3) color case.
in the SU(3) color case.
We use one-loop level renormalization-group-improved coupling in the case of ![]() and
and![]() ,
,
![]()
Figure 1. The Schwinger-Dyson equation for the quark field. The shaded blob denotes the self-energy of the quark![]() , the black dot the bare quark-gluon vertex, the shaded triangle the dressed vertex
, the black dot the bare quark-gluon vertex, the shaded triangle the dressed vertex![]() , the solid line the quark propagator and the curly line the gluon propagator.
, the solid line the quark propagator and the curly line the gluon propagator.
![]() (6)
(6)
with an infrared regularization of a simple cut at ![]() which leads to
which leads to![]() , and the QCD scale parameter
, and the QCD scale parameter ![]() [4] [73] [77] . The subscript E, such as
[4] [73] [77] . The subscript E, such as![]() , denotes the value in Euclidean space. The infrared regularization has been introduced to avoid the divergent pole at
, denotes the value in Euclidean space. The infrared regularization has been introduced to avoid the divergent pole at![]() . The behavior of the coupling is shown in Figure 2 in the Euclidean space. All the figures for the numerical results will be in the Euclidean space.
. The behavior of the coupling is shown in Figure 2 in the Euclidean space. All the figures for the numerical results will be in the Euclidean space.
The Higashijima-Miransky approximation is to take the larger value of the argument (Euclidean momenta) in the coupling as![]() , and this approximation is also frequently used in the SD approach for quarks, because
, and this approximation is also frequently used in the SD approach for quarks, because ![]() is analytically obtained in the Landau gauge and the computation becomes quite simplified for the quark self-energy
is analytically obtained in the Landau gauge and the computation becomes quite simplified for the quark self-energy![]() :
:
![]() (7)
(7)
where the Wick rotation has been taken. (For the detail, see, e.g., Appendix in Ref. [73] .) The result of the SD equation is shown in Figure 3 in the chiral limit![]() . There is a small cusp structure at
. There is a small cusp structure at ![]() due to the coupling behavior Equation (6). The ultraviolet cutoff
due to the coupling behavior Equation (6). The ultraviolet cutoff ![]() is taken as 5 GeV. The self-energy
is taken as 5 GeV. The self-energy ![]() is
is
![]()
Figure 2. The behavior of the running coupling of our model ![]() as a function of the momentum p in the Euclidean space. The thin line is the one-loop renormalization group improved running coupling. We introduce a simple cut at
as a function of the momentum p in the Euclidean space. The thin line is the one-loop renormalization group improved running coupling. We introduce a simple cut at ![]() as an infrared regularization.
as an infrared regularization.
![]()
Figure 3. The quark self-energy ![]() as a function of the momentum p in the chiral limit. The self-energy is large in the low momentum region and goes to zero monotonously with the momentum.
as a function of the momentum p in the chiral limit. The self-energy is large in the low momentum region and goes to zero monotonously with the momentum.
unchanged even the cutoff is taken 10 GeV. The quark mass is large at the infrared region and monotonously goes to zero with the momentum, which reflects spontaneous chiral-symmetry breaking [2] - [4] [88] .
The scale parameter ![]() is chosen to reproduce chiral properties for quarks in the SD formalism with the Higashijima-Miransky approximation in the Landau gauge, while the ordinary QCD scale parameter is around
is chosen to reproduce chiral properties for quarks in the SD formalism with the Higashijima-Miransky approximation in the Landau gauge, while the ordinary QCD scale parameter is around![]() . The self-energy leads to the pion decay constant with the Pagels-Stokar approximation [89] :
. The self-energy leads to the pion decay constant with the Pagels-Stokar approximation [89] :
![]() (8)
(8)
and the (unrenormalized) chiral condensate:
![]() (9)
(9)
Since the pion decay constant is a physical value, its renormalization is not required and it does not depend on the ultraviolet cutoff![]() . Hence, the upper limit of the integration has been taken as
. Hence, the upper limit of the integration has been taken as![]() . On the other hand, the chiral condensate depends on the renormalization point. We adopt a standard renormalization point
. On the other hand, the chiral condensate depends on the renormalization point. We adopt a standard renormalization point
![]() [1] , and consider the chiral condensate
[1] , and consider the chiral condensate ![]() according to the renormalization-group formula [73] [74] [77] :
according to the renormalization-group formula [73] [74] [77] :
![]() (10)
(10)
with ![]() and
and ![]() corresponding to the lowest coefficient of the
corresponding to the lowest coefficient of the ![]() function of the renormalization group. Taking the scale parameter
function of the renormalization group. Taking the scale parameter ![]() as 500 MeV and the ultraviolet cutoff
as 500 MeV and the ultraviolet cutoff ![]() as 5 GeV, the pion decay constant and the chiral condensate are fixed as
as 5 GeV, the pion decay constant and the chiral condensate are fixed as ![]() and
and![]() ,
,
respectively. We have numerically checked that they are stable against the variation of the ultraviolet cutoff![]() . The SD formalism with the approximations in the Landau gauge reproduces these chiral properties well.
. The SD formalism with the approximations in the Landau gauge reproduces these chiral properties well.
3. The Schwinger-Dyson Equation for the Scalar Diquark
In this section, we investigate the scalar diquark, i.e., an extended colored scalar object, and its mass generation, using the Schwinger-Dyson (SD) formalism.
Diquark is a bound-state-like object of two quarks and decomposed into color anti-triplet ![]() and sextet
and sextet ![]() and flavor anti-triplet
and flavor anti-triplet ![]() and sextet
and sextet ![]() in SU(3) flavor case. The most attractive channel for diquark is the color and flavor anti-triplet
in SU(3) flavor case. The most attractive channel for diquark is the color and flavor anti-triplet ![]() and spin singlet with even parity
and spin singlet with even parity ![]() by one gluon exchange [16] [17] and by instanton interactions [90] [91] , which is called scalar diquark. If the diquark correlation is developed in a hadron such as a heavy baryon (
by one gluon exchange [16] [17] and by instanton interactions [90] [91] , which is called scalar diquark. If the diquark correlation is developed in a hadron such as a heavy baryon (![]() ), this scalar diquark channel would be favored. We consider the scalar
), this scalar diquark channel would be favored. We consider the scalar
diquark as an effective degree of freedom with a peculiar size, assuming it to be an extended scalar field ![]() [10] [42] like a meson in the effective hadron models. The scalar diquark is composed of two quarks with the gluonic interaction, and still affected by non-perturbative gluonic effects since it has non-zero color charge as shown Figure 4. The dynamics of the scalar diquark field
[10] [42] like a meson in the effective hadron models. The scalar diquark is composed of two quarks with the gluonic interaction, and still affected by non-perturbative gluonic effects since it has non-zero color charge as shown Figure 4. The dynamics of the scalar diquark field ![]() is expected to be described by the gauge-invariant scalar-QCD-type Lagrangian:
is expected to be described by the gauge-invariant scalar-QCD-type Lagrangian:
![]()
![]() (11)
(11)
where the bare diquark mass ![]() and the gauge field
and the gauge field ![]() (gluon) with the generator
(gluon) with the generator ![]() have been introduc-
have been introduc-
![]() (a) (b)
(a) (b)
Figure 4. The two types of gluonic interaction for a diquark: (a) inter-two-quarks gluonic interaction to form a diquark and (b) gluonic dressing for the diquark due to its non-zero color charge. The single line denotes a quark, the double line a diquark and the curly line a gluon.
ed. We note that the scalar diquark has the 4-point interaction term of ![]() type, which is different from the quark. In general, such gauged scalar fields accompany the 4-point interaction [79] [82] - [84] [92] .
type, which is different from the quark. In general, such gauged scalar fields accompany the 4-point interaction [79] [82] - [84] [92] .
Since the diquark is a bound-state-like object confined in a hadron, it must have an effective size and its size should be smaller than the hadron. In order to include the size effect of diquark, we introduce a simple “form factor” in the four-dimensional Euclidean space as
![]() (12)
(12)
where the momentum cutoff ![]() corresponds to the inverse of the diquark size R. In this paper, we set
corresponds to the inverse of the diquark size R. In this paper, we set![]() . Since the radiative correction for the scalar particle is generally large, this form factor has also a role of the convergence factor. As for the form factor
. Since the radiative correction for the scalar particle is generally large, this form factor has also a role of the convergence factor. As for the form factor![]() , it has the roles of introducing an effective size and convergence of the SD equation, so one can use arbitrary function such as the step function
, it has the roles of introducing an effective size and convergence of the SD equation, so one can use arbitrary function such as the step function![]() , the exponential function
, the exponential function ![]() and so on. In this study, we take Equation (12) with
and so on. In this study, we take Equation (12) with ![]() to simple analysis and the convergence of the SD equation. The size effect of the diquark can be included in the vertex as
to simple analysis and the convergence of the SD equation. The size effect of the diquark can be included in the vertex as![]() .
.
While the scalar QCD Lagrangian (11) is renormalizable, this theory is an effective cutoff theory with an UV cutoff parameter![]() , which corresponds to the inverse size of the scalar diquark. Here, the scalar diquark cannot be observed as an isolated object, and has no characteristic symmetry, such as the chiral symmetry, so that it is difficult to set the renormalization condition. Instead, we introduce an effective size
, which corresponds to the inverse size of the scalar diquark. Here, the scalar diquark cannot be observed as an isolated object, and has no characteristic symmetry, such as the chiral symmetry, so that it is difficult to set the renormalization condition. Instead, we introduce an effective size ![]() of the diquark, which leads to a natural UV cutoff in the theory. As we will see later, the effective size of diquark will play an important role for the convergent of loop integrations, and therefore we will not take the limit of
of the diquark, which leads to a natural UV cutoff in the theory. As we will see later, the effective size of diquark will play an important role for the convergent of loop integrations, and therefore we will not take the limit of ![]() (
(![]() ). In fact, the extended diquark is treated as the effective degrees of freedom appearing in the QCD system of quarks and gluons, and hence, also for the scalar diquark, we basically use the same framework as the
). In fact, the extended diquark is treated as the effective degrees of freedom appearing in the QCD system of quarks and gluons, and hence, also for the scalar diquark, we basically use the same framework as the
single quark case, presented in the previous section. For instance, we will use the same running coupling ![]() in Equation (6) for the argument of diquarks.
in Equation (6) for the argument of diquarks.
We now describe the SD equation for the scalar diquark, as shown in Figure 5. For the self-energy diagram, we include the first order of the coupling ![]() at the one-loop level, like the improved ladder QCD [3] [4] [73] [74] . Note however that, due to the iterative calculation, this formalism includes infinite order of the coupling
at the one-loop level, like the improved ladder QCD [3] [4] [73] [74] . Note however that, due to the iterative calculation, this formalism includes infinite order of the coupling ![]() and describes non-perturbative effects. It is also notable that the same form of the running coupling for the quark/gluon coupling can be used even for the scalar diquark/gluon [93] [94] . (In particular, in the heavy mass limit of colored particles, the QCD interaction depends only on their color.) Since the scalar diquark corresponds to an antiquark in terms of the color representation, we may use the same form of the running coupling even for the scalar diquark case. Then, the SD equation for the scalar diquark is diagrammatically expressed as Figure 5 and is written by
and describes non-perturbative effects. It is also notable that the same form of the running coupling for the quark/gluon coupling can be used even for the scalar diquark/gluon [93] [94] . (In particular, in the heavy mass limit of colored particles, the QCD interaction depends only on their color.) Since the scalar diquark corresponds to an antiquark in terms of the color representation, we may use the same form of the running coupling even for the scalar diquark case. Then, the SD equation for the scalar diquark is diagrammatically expressed as Figure 5 and is written by
![]() (13)
(13)
![]()
Figure 5. The Schwinger-Dyson equation for the scalar diquark. The shaded blob is the self-energy![]() , the dashed line denotes the scalar diquark propagator and the curly line the gluon propagator. The last term arisig from 4-point interaction is the peculiar term in gauged scalar theories, and it does not appear in the single quark case in QCD.
, the dashed line denotes the scalar diquark propagator and the curly line the gluon propagator. The last term arisig from 4-point interaction is the peculiar term in gauged scalar theories, and it does not appear in the single quark case in QCD.
In the right-hand side of Equation (13), the second term arises from the 4-point vertex and the third term is lead from the 3-point vertex, as shown in Figure 5. Here, we do not consider the wave functional renor- malization, as is often assumed for the quark field in the Landau gauge. Similarly in the single quark case, we adopt the Higashijima-Miransky approximation ![]() for the 3-point vertex, and finally obtain the SD equation for the self-energy
for the 3-point vertex, and finally obtain the SD equation for the self-energy ![]() of the scalar diquark:
of the scalar diquark:
![]() (14)
(14)
4. Numerical Results and Discussion
4.1. The Parameter Setting
The bare mass ![]() and cutoff
and cutoff ![]() (inverse of the size R) are free parameters of the diquark theory. In this subsection, we consider the possible range of these parameters from the physical viewpoint.
(inverse of the size R) are free parameters of the diquark theory. In this subsection, we consider the possible range of these parameters from the physical viewpoint.
The diquark is originally made of two consistent quarks, and the color-Coulomb interaction is one of the main attractive forces. We here estimate the color-Coulomb interaction between the two massive quarks from the
three-quark (3Q) potential [99] , or generally from the mult-quark potential such as 4Q(![]() ) and 5Q(
) and 5Q(![]() ) potentials [100] . In SU(3) lattice QCD, the 3Q potential among the three quarks located at
) potentials [100] . In SU(3) lattice QCD, the 3Q potential among the three quarks located at ![]() is well reproduced by
is well reproduced by
![]() (15)
(15)
with the color-Coulomb coefficient![]() , the string tension
, the string tension ![]() and the minimal flux-tube length
and the minimal flux-tube length ![]() [99] . Since the color-Coulomb potential energy between two quarks is
[99] . Since the color-Coulomb potential energy between two quarks is ![]() for the inter-quark distance R, the potential energy is estimated as
for the inter-quark distance R, the potential energy is estimated as ![]() for the typical range of
for the typical range of![]() , and its value is not so large in comparison with the two-quark mass of about 600 MeV. [Note also that similar estimation also leads to a small value of the diquark-diquark interaction, which gives a reason of the absence of
, and its value is not so large in comparison with the two-quark mass of about 600 MeV. [Note also that similar estimation also leads to a small value of the diquark-diquark interaction, which gives a reason of the absence of ![]() in the diquark Lagrangian (11).] The same result can be obtained from the multi-quark potential [100] , because the color-Coulomb coefficient is the same for two quarks in the diquark, i.e.,
in the diquark Lagrangian (11).] The same result can be obtained from the multi-quark potential [100] , because the color-Coulomb coefficient is the same for two quarks in the diquark, i.e., ![]() for n = 3, 4, 5. Therefore, the bare mass of diquark is expected to be simply considered as the twice of the quark mass.
for n = 3, 4, 5. Therefore, the bare mass of diquark is expected to be simply considered as the twice of the quark mass.
In this paper, we consider two cases of the bare diquark mass. One is twice of constituent quark mass, i.e.,![]() . The other is twice of the running quark self-energy, i.e.,
. The other is twice of the running quark self-energy, i.e., ![]() , where
, where ![]()
is determined by the SD equation for single quark Equation (7). This means that the diquark is constructed by the two dressing quarks. The constant bare mass case is based on the constituent quark model like picture and the running bare mass case is the SD formalism with omitting the effect of the gluonic attraction force between two quarks. The diquark should be dressed by gluon furthermore because of its non-zero color charge.
The cutoff ![]() corresponds to the diquark size in a hadron, R, i.e.,
corresponds to the diquark size in a hadron, R, i.e., ![]() , so the diquark should be smaller than the hadron. We also consider two cases of the size. One is the typical size of a baryon,
, so the diquark should be smaller than the hadron. We also consider two cases of the size. One is the typical size of a baryon, ![]() , i.e.,
, i.e., ![]() , which gives the upper limit of the size (the lower limit of the cutoff). The diquark covers the baryon in this case. The second is the typical size of a constituent quark,
, which gives the upper limit of the size (the lower limit of the cutoff). The diquark covers the baryon in this case. The second is the typical size of a constituent quark, ![]() , i.e.,
, i.e., ![]() , which gives the lower limit of the size (the upper limit of the cutoff).
, which gives the lower limit of the size (the upper limit of the cutoff).
4.2. The Constant Bare Mass Case
We first show in Figure 6 the case of the constant bare mass ![]() with dependence on the cutoff
with dependence on the cutoff![]() . The diquark self-energy
. The diquark self-energy ![]() is always larger than the bare mass
is always larger than the bare mass ![]() and almost constant except for a small bump structure in an infrared region. The value of the self-energy is strongly depends on the cutoff
and almost constant except for a small bump structure in an infrared region. The value of the self-energy is strongly depends on the cutoff![]() , e.g., the “compact diquark” with
, e.g., the “compact diquark” with ![]() has a large mass.
has a large mass.
The scalar QCD includes both 3-point and 4-point interactions, and the existence of 4-point interaction is diagrammatically different from the ordinary QCD. To see the role of each interaction, we consider the calculation of the artificial removal of 3-point interaction and 4-point interaction, respectively. In fact, we investigate the two cases: (a) removal of 4-point interaction and (b) removal of 3-point interaction. The result is shown in Figure 7 in the case of![]() . The bump structure appears in the case without the 4-point interaction term as shown in Figure 7(a). Although the diagrammatic expression of the SD equation for the scalar
. The bump structure appears in the case without the 4-point interaction term as shown in Figure 7(a). Although the diagrammatic expression of the SD equation for the scalar
diquark without 4-point interaction term is analogous to the quark SD equation, the behavior is completely
different from the quark case. The diquark self-energy ![]() starts from the bare mass
starts from the bare mass ![]() at zero momentum, then decreases at low momentum and rises up to the original value 600 MeV. On the other hand, the quark self-energy
at zero momentum, then decreases at low momentum and rises up to the original value 600 MeV. On the other hand, the quark self-energy ![]() starts from a large value and goes to zero monotonously with the momentum. The
starts from a large value and goes to zero monotonously with the momentum. The
SD equation without 3-point interaction just rises the self-energy and keeps constant. The strong dependence of the cutoff ![]() (or the size R) mainly comes from the 4-point interaction term.
(or the size R) mainly comes from the 4-point interaction term.
4.3. The Running Bare Mass Case
We show in Figure 8 the case of the running bare mass ![]() with dependence on the cutoff
with dependence on the cutoff![]() . The diquark self-energy
. The diquark self-energy ![]() also strongly depends on the cutoff
also strongly depends on the cutoff![]() . In the low-momentum region, the behavior of
. In the low-momentum region, the behavior of ![]() reflects the running property of the bare mass, especially in the
reflects the running property of the bare mass, especially in the ![]() case, the gluonic effect seems to be small, because of
case, the gluonic effect seems to be small, because of![]() . In the high-momentum region, the diquark self-energy keeps a large value, while the bare mass
. In the high-momentum region, the diquark self-energy keeps a large value, while the bare mass ![]() goes to zero. This suggests the mass generation of the scalar diquark by gluonic radiative correction.
goes to zero. This suggests the mass generation of the scalar diquark by gluonic radiative correction.
4.4. Discussion on the Scalar Diquark Property
In this subsection, we discuss the mass and the size of the scalar diquark, with comparing to the chiral quark. One of the most important properties of single quark SD equation (7) is the existence of the trivial solution ![]() in the chiral limit
in the chiral limit![]() . In fact, the quark mass remains to be zero due to the chiral symmetry in the perturbative treatment, and the quark mass generation, i.e., chiral symmetry breaking, is realized by the non-perturbative gluonic interaction [3] [4] . Such arguments can be done even in the limit of
. In fact, the quark mass remains to be zero due to the chiral symmetry in the perturbative treatment, and the quark mass generation, i.e., chiral symmetry breaking, is realized by the non-perturbative gluonic interaction [3] [4] . Such arguments can be done even in the limit of![]() , which is consistent with the point quark as an elementary particle.
, which is consistent with the point quark as an elementary particle.
On the other hand, the SD equation (13) for scalar diquark has no trivial solution and is a highly non-linear equation, even in the zero bare mass limit![]() . For example, the 4-point interaction term gives a strong dependence of the UV cutoff
. For example, the 4-point interaction term gives a strong dependence of the UV cutoff![]() . This is similar to the framework of GUT, where the Higgs scalar field suffers from a large radiative correction of the GUT energy scale.
. This is similar to the framework of GUT, where the Higgs scalar field suffers from a large radiative correction of the GUT energy scale.
Actually, the scalar diquark self-energy ![]() strongly depends on the diquark size
strongly depends on the diquark size ![]() in both cases of the bare mass. In an extreme case of the point-like limit
in both cases of the bare mass. In an extreme case of the point-like limit![]() , i.e.,
, i.e., ![]() , the diquark effective mass diverges. This suggests that the simple treatment of point-like diquarks is somehow dangerous in hadron models and the diquark must have an effective size.
, the diquark effective mass diverges. This suggests that the simple treatment of point-like diquarks is somehow dangerous in hadron models and the diquark must have an effective size.
As a quantitative argument, our calculations show that the “compact diquark” with ![]() has a large effective mass in both cases, and does not seem to be acceptable in effective models for hadrons. In fact, the appropriate diquark is not so compact as
has a large effective mass in both cases, and does not seem to be acceptable in effective models for hadrons. In fact, the appropriate diquark is not so compact as ![]() but is fairly extended as
but is fairly extended as![]() .
.
4.5. Mass Generation for Colored Scalar Particle
Finally, we consider the zero bare-mass case of diquark,![]() . Even for a finite mass of quark, the bare mass of diquark can be zero, if the attraction between two quarks extremely strong. The result is shown in Figure 9 for the two cases: (a)
. Even for a finite mass of quark, the bare mass of diquark can be zero, if the attraction between two quarks extremely strong. The result is shown in Figure 9 for the two cases: (a) ![]() and (b)
and (b) ![]() on the cutoff. The self-energy
on the cutoff. The self-energy ![]() is always
is always
finite and takes a large value even for![]() . The mass generation mechanism in QCD is usually considered in the context of spontaneous chiral-symmetry breaking. On the other hand, our scalar diquark theory is composed
. The mass generation mechanism in QCD is usually considered in the context of spontaneous chiral-symmetry breaking. On the other hand, our scalar diquark theory is composed
of an effective scalar diquark field ![]() and does not have the chiral symmetry explicitly, although the
and does not have the chiral symmetry explicitly, although the
original diquark is constructed by two chiral quarks. Nevertheless, the effective mass of diquark emerges by the non-perturbative gluonic effect. In fact, the mechanism of dynamical mass generation seems to work in the
scalar diquark theory, even without chiral symmetry breaking. If we take![]() , the diquark self-energy is
, the diquark self-energy is![]() . This result seems to be consistent with the lattice QCD result on the colored scalar particle [10] .
. This result seems to be consistent with the lattice QCD result on the colored scalar particle [10] .
5. Conclusion and Discussion
We have studied various mass generation of colored particles and gluonic dressing effect in a non-perturbative manner, using the Schwinger-Dyson (SD) formalism in QCD. First, we have briefly reviewed dynamical quark-mass generation in QCD in the SD approach as a typical fermion-mass generation via spontaneous chiral-symmetry breaking. Second, using the SD formalism for scalar QCD, we have investigated the scalar diquark, a bound-state-like object of two quarks, and its mass generation, which is clearly non-chiral-origin. Considering the possible size of the diquark inside a hadron, the effect of diquark size R is introduced as a cutoff
parameter ![]() in the form factor, as is used in effective theories.
in the form factor, as is used in effective theories.
The basic technology of scalar SD formalism is imported from the single quark case, such as the running coupling, the approximations and so on. Since the diquark is located in and construct of a hadron, the size should be smaller than the hadron (![]() ) and larger than the constituent quark (
) and larger than the constituent quark (![]() ). The size (cutoff) dependence of self-energy have been investigated. We have considered the two cases of the constant
). The size (cutoff) dependence of self-energy have been investigated. We have considered the two cases of the constant
bare mass ![]() and the running bare mass
and the running bare mass![]() . The diquark self-energy strongly depends on the size
. The diquark self-energy strongly depends on the size ![]() in both cases, especially the small diquark (
in both cases, especially the small diquark (![]() ) has a large effective mass by the gluonic dressing effect.
) has a large effective mass by the gluonic dressing effect.
We find that the effective diquark mass is finite and large even for the zero bare-mass case, and the value strongly depends on the size R, which is an example of dynamical mass generation by the gluonic effect, without chiral symmetry breaking. The mass difference between current and constituent charm quark mass and the large glueball mass are also examples of this type of mass generation. In this sense, spontaneous chiral-symmetry breaking may be a special case of massless (or small mass) fermion. As was conjectured in Ref. [10] , it would be a general property of strong interacting theory that all colored particles acquire a large effective mass by the dressing effect, as shown in Figure 10.
![]()
Figure 10. The schematic picture for dynamical mass generation of the colored particle. The colored particle (solid line) interacting with the gluons (curly line). The effective mass emerges by the non-perturbative interaction even without the chiral symmetry.
In this study, we have mainly investigated the diquark properties, and have not calculated physical quantities. It is however desired to describe the color-singlet states such as heavy baryon ![]() based on the scalar theory. One of description of diquark based on QCD is the Bethe-Salpeter (BS) formalism for two quarks [95] - [98] . However, the treatment of the scalar diquark as an explicit degree of freedom
based on the scalar theory. One of description of diquark based on QCD is the Bethe-Salpeter (BS) formalism for two quarks [95] - [98] . However, the treatment of the scalar diquark as an explicit degree of freedom ![]() is a good approximation for the structure of the heavy baryons. The constituent scalar-quark(diquark)/quark picture in the scalar lattice QCD [10] and the structure of
is a good approximation for the structure of the heavy baryons. The constituent scalar-quark(diquark)/quark picture in the scalar lattice QCD [10] and the structure of ![]() (
(![]() quarks) with explicit diquark degree of freedom using QCD sum rule [42] have been discussed. The description of the heavy baryon as heavy quark/diquark (
quarks) with explicit diquark degree of freedom using QCD sum rule [42] have been discussed. The description of the heavy baryon as heavy quark/diquark (![]() ) using the BS equation will be investigated as our future work.
) using the BS equation will be investigated as our future work.
The tetra-quark states ![]() may include diquark/antidiquark components. Although the two mesons molecular states may dominate in the tetra-quark due to the strong correlation between quark and antiquark, the diquark/antidiquark would be also important components [21] - [25] . The tetra-quark states would be described as the linear combination of two mesons and diquark/antidiquark states based on the BS formalism. The structure of sigma meson (light scalar mesons) is also applicable subject. The sigma meson is considered as a chiral partner of the pion in the context of the chiral symmetry, which structure is quark/antiquark bound state. The possibility of the light scalar mesons as four-quark states have been discussed [20] [23] - [35] . The structure of the sigma meson (light scalar mesons) can be described as the linear combination of quark/antiquark, diquark/antidiquark and two mesons in the context of the BS formalism.
may include diquark/antidiquark components. Although the two mesons molecular states may dominate in the tetra-quark due to the strong correlation between quark and antiquark, the diquark/antidiquark would be also important components [21] - [25] . The tetra-quark states would be described as the linear combination of two mesons and diquark/antidiquark states based on the BS formalism. The structure of sigma meson (light scalar mesons) is also applicable subject. The sigma meson is considered as a chiral partner of the pion in the context of the chiral symmetry, which structure is quark/antiquark bound state. The possibility of the light scalar mesons as four-quark states have been discussed [20] [23] - [35] . The structure of the sigma meson (light scalar mesons) can be described as the linear combination of quark/antiquark, diquark/antidiquark and two mesons in the context of the BS formalism.
Acknowledgements
S.I. thanks T.M. Doi, H. Iida and N. Yamanaka for useful discussion and comments. This work is in part sup- ported by the Grant for Scientific Research [Priority Areas “New Hadrons” (E01:21105006), (C) No.23540306, No.15K05076] from the Ministry of Education, Culture, Science and Technology of Japan.