Received 7 January 2016; accepted 24 April 2016; published 28 April 2016

1. Introduction
Monopile is a popular foundation design for wind turbine power generation systems. Main advantage of this type of foundation is its simplicity in both fabrication and installation. Conventional monopile design consists of a cylindrical pipe like structure constructed from steel plates that are rolled and longitudinally welded into cans. The cans are then stacked and circumferentially welded to make up the conventional monopile. The thickness of plate can be varied from section to section in proportion with the in-service stressing at specific locations. Some of the more costly designs also include conical sections to assist joining of the wind turbine to the foundation.
Typically monopiles are installed by hammer pile driving whereby the monopile is erected upright, either onshore or offshore, with a cap and hammer placed on top. The cap is used to transfer hammer blows to the pile evenly across the pile section. The hammer consists of a drop weight travelling inside a channel to guide it. Generally the drop weight is raised by a hydraulic ram, once at its highest point of travel, potential gravitational energy of the drop weight is ready to be released. The weight is either released in free fall or accelerated downwards by pneumatic, hydraulic or combustible means. Each consecutive hammer blow drives the pile further into the ground.
Research into pile driving operation has focused primarily on investigation of load bearing resistance of the foundation. Smith has developed a pile driving analysis based upon one dimensional wave equation [1] . The original model by Smith has been developed further to accommodate various hammer types and soil conditions and has undergone extensive validation studies. The result of these developments is modern commercial software available for the use of engineers [2] . However, prediction of stressing induced in the pile is limited. The model is able to predict global dynamic stressing of the pile and by extension residual stress due to soil interaction, post piling [3] . Local pile stressing during installation is not documented.
Typical service life of an offshore wind turbine energy generating system is approximately 25 years. Therefore all components, including the foundation, must be structurally sound for at least that period of time. Conventional monopile foundation design procedure seeks to determine the fatigue life based on in-service loads, which do not typically include piling installation fatigue damage, yet it has been seen, in some cases, that monopile foundation can be visibly damaged during installation. The question is whether the fatigue damage due to installation can be significant under certain circumstances. In order to determine fatigue damage dealt to the pile during the installation, local stressing of the welds is of concern. Therefore the interest of this paper is determining of local weld stressing due to pile driving installation and by extension fatigue damage, thereby dealt to a monopile wind turbine foundation.
The work presented in this paper was part of a larger project, the goal of which was to establish the feasibility of utilising a novel faceted monopile design. General summary of the results of that study was published by the authors [4] . The feasibility of the faceted monopile design was considered based on the structural performance comparison with a conventional circular monopile design. Scaled down piling test was conducted while strain was measured at key locations by utilisation of resistive strain gauges. Both the conventional circular and novel faceted test pieces were used to quantify the stresses induced during piling. Also the difference between circular and faceted sections was of interest to support the feasibility of the faceted design.
2. Materials and Methods
To simulate the pile driving installation a scaled down test was conducted as illustrated in Figure 1. Equipment representative of full scale installation was used, namely the BSP CXL 140 hydraulic hammer. A circular reference monopile was available at the testing ground. The circular monopile had already been embedded to a depth of approximately 30m. Such depth of embedment results in high friction forces between the monopile and surrounding soil. As a consequence the test would be conducted at stall condition, meaning that little or no further embedment of the monopile can be expected.
The faceted test piece was welded on top of the circular reference monopile. Bespoke cap was manufactured to fit the faceted geometry. A polymer dolly inside the cap was used to transfer the impact from the hammer to the cap and further to the monopile.
To determine stressing induced in the monopile due to impacts from hammer blows, a number of measurement points were chosen and are shown in Figure 2. For the faceted test piece 16 measurement points were identified. An additional 4 measurement points were selected for the circular reference pile. Placement of the gauges was such so as to attempt to capture the behaviour of interest:
・ Stresses at the weld, on both the inner and outer faces of the circular and faceted test pieces.
・ Stresses in the mid face of the plate of the faceted design, on both the inner and outer faces.
・ Misalignment of the hammer impact and hence the maximum loading.
・ Stress distribution along the length of the faceted test piece thus establishing the stress near the impact zone.
Due to the complex nature of impact loading, the orientation of the principal stresses was unknown prior to testing. It was predicted that significant loading would be present in the direction of the hammer blow. However it was understood that the orientation of the principal stresses may change near the corner welds. It was therefore decided to use R rosette strain gauges. These specialised strain gauges allow measurement of the stresses at the surface of the material in any direction. Each rosette contains three separate strain gauges aligned at 0˚, 45˚ and
![]()
Figure 2. Strain gauge measurement points.
90˚. From these three strain measurements it is possible to resolve principal normal stresses and their directions. Example wired R rosette is illustrated in Figure 3. The equation relating strains and principal stresses is [5] :
 (1)
(1)
whereby the direction of the maximum principal stress with respect to the orientation of strain 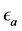 is:
is:
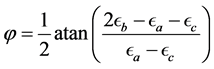 (2)
(2)
where:
 Elastic modulus,
Elastic modulus,
 Poison’s ratio,
Poison’s ratio,
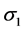 Maximum principal stress,
Maximum principal stress,
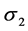 Minimum principal stress,
Minimum principal stress,
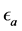 Strain measured by gauge aligned with 0˚,
Strain measured by gauge aligned with 0˚,
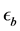 Strain measured by gauge aligned with 45˚,
Strain measured by gauge aligned with 45˚,
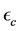 Strain measured by gauge aligned with 90˚,
Strain measured by gauge aligned with 90˚,
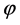 Direction of the maximum principal stress with respect to strain
Direction of the maximum principal stress with respect to strain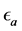 .
.
For the test to be scaled up with validity, similarity in geometry and stressing must be satisfied [6] . Similarity in geometry is satisfied by the shape and dimensional ratios. The shape of the faceted test piece is an equal sided decagon which is the same shape envisaged for full size novel faceted design. Also the circumscribed diameter to thickness ratio of the test piece is equal to full scale faceted monopile. The conventional circular test piece satisfies geometrical similarity in shape however the diameter to thickness ratio is slightly different. There was no choice in the dimensions of the circular test piece, as this was predetermined by the availability at the hammer testing ground. An effort to correct this discrepancy has been made and is described in later paragraphs.
Once the geometrical similarity is satisfied, it is assumed that the stress in geometrically similar structures is a function of hammer impact energy E, geometrical area of the cross section A and hammering equipment setup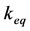 . The stress is expressed in the following form:
. The stress is expressed in the following form:
![]() (3)
(3)
which satisfied dimensional equality:
![]() (4)
(4)
The test hammer equipment is representative of the full scale hammering equipment setup. Therefore it is assumed that ![]() is equal for both the test and full scale conditions. In order to achieve test stressing equivalent to full scale:
is equal for both the test and full scale conditions. In order to achieve test stressing equivalent to full scale:
![]() (5)
(5)
Faceted test piece hammer impact energy ![]() as derived from Equations (3) and (5) is:
as derived from Equations (3) and (5) is:
![]() (6)
(6)
![]() (7)
(7)
The test hammer impact energies for the faceted ![]() and circular
and circular ![]() test pieces are equal:
test pieces are equal:
![]() (8)
(8)
The stressing of the full scale circular conventional monopole ![]() during installation as derived from Equations (3) and (8) is:
during installation as derived from Equations (3) and (8) is:
![]() (9)
(9)
![]() (10)
(10)
where:
![]() Monopile stress,
Monopile stress,
![]() Hammer impact energy,
Hammer impact energy,
![]() Monopile cross sectional area,
Monopile cross sectional area,
![]() Constant relating to pile installation equipment setup,
Constant relating to pile installation equipment setup,
![]() Constant relating to faceted monopile test energy scaling,
Constant relating to faceted monopile test energy scaling,
![]() Constant relating to circular monopile test stress scaling.
Constant relating to circular monopile test stress scaling.
Subscripts:
![]() Relating to test faceted monopile,
Relating to test faceted monopile,
![]() Relating to full scale faceted monopile,
Relating to full scale faceted monopile,
![]() Relating to test conventional circular monopile,
Relating to test conventional circular monopile,
![]() Relating to full scale conventional circular monopile.
Relating to full scale conventional circular monopile.
The test hammer impact energy was based on data gathered from a commercial installation. A pile driving history for a similar full scale conventional monopile design is illustrated in Figure 4. The data shows that a
significant number of impactsoccur around 1000 kNm per blow. Above 800 kNm per blow there are approximately 2000 blows. Therefore the pile driving history was simplified to 1000 kNm per blow at 2000 blows.
From the geometrical dimensions of the full scale and test size monopiles presented in Table 1, the test hammer blow energy and other test scaling parameters are calculated and presented in Table 2. The scaled down piling installation test was conducted at the constant impact energy of 38 KNm.
3. Results and Analysis
Typical resistive strain gauge measurement requires that the stress field prior to measurement is qualitatively understood. Strain gauges are then aligned to the principal strains in that field. However due to the complex nature of impact loading, the use of R rosette was warranted, which was described in more detail in the previous section. From the measurement of such rosette, magnitude of principal stresses in any direction can be calculated and it is not necessary to align the strain gauge with the principal strains.
An example of results from measurement point 1i is presented. Figure 5(a) illustrates the principal stresses during a single impact. Figure 5(b) illustrates the angular orientation ![]() of the maximum principal stress σ1 for the same time range. The reference for the angular orientation is the axis running through the centre of the test piece. The minimum principal stress
of the maximum principal stress σ1 for the same time range. The reference for the angular orientation is the axis running through the centre of the test piece. The minimum principal stress ![]() orientation is +90˚ from
orientation is +90˚ from![]() . The data shows that during the main impulse
. The data shows that during the main impulse ![]() is almost 90˚, which means that the maximum principal stress
is almost 90˚, which means that the maximum principal stress ![]() is in the circumferential direction of the monopile. The minimum principal stress
is in the circumferential direction of the monopile. The minimum principal stress ![]() is in the longitudinal direction of the test piece which coincides with the direction of the hammer impact. Immediately after the main impulse, ringing of the test piece is observed. Stress waves travelling up and down the test piece superimpose to produce a complex stress field with unstable orientation.
is in the longitudinal direction of the test piece which coincides with the direction of the hammer impact. Immediately after the main impulse, ringing of the test piece is observed. Stress waves travelling up and down the test piece superimpose to produce a complex stress field with unstable orientation.
Data across the range of measurement points and across the full number of 34 impacts observed, shows that the minimum principal stress![]() , during the main impulse, is always aligned with the direction of the hammer impact, as was expected. The maximum deviation from the direction of the hammer impact is around ±10˚ near the faceted test piece corners and is less elsewhere. Since the cosine of 10˚ results in the error of less than 2%, minimum principal stress
, during the main impulse, is always aligned with the direction of the hammer impact, as was expected. The maximum deviation from the direction of the hammer impact is around ±10˚ near the faceted test piece corners and is less elsewhere. Since the cosine of 10˚ results in the error of less than 2%, minimum principal stress![]() , during the main impulse, will effectively be regarded as acting in the longitudinal direction of the test piece. The magnitudes of the maximum principal stress σ1, during the main impulse will effectively be regarded as acting in the circumferential direction of the test piece.
, during the main impulse, will effectively be regarded as acting in the longitudinal direction of the test piece. The magnitudes of the maximum principal stress σ1, during the main impulse will effectively be regarded as acting in the circumferential direction of the test piece.
The polymer dolly and cap assembly was used to evenly transfer the impact from the hammer to the test piece, however an amount of misalignment was still expected. Because of the limited number of measurement points it was feared that the maximum stressed regions would be missed. Hence the layout of the measurement points was planned in such a way so as to allow an estimation of the hammer impact misalignment with the minimum number of measurement points. Once the misalignment is understood the position and magnitude of maximum stress can be estimated. The gauges were placed around the circumference of both test pieces (see Figure 2). To estimate the impact misalignment, stress between circumferential gauges was extrapolated. An example of the extrapolation for the circular test piece is illustrated in the polar plot of Figure 6. The angular axis corresponds
![]()
Figure 5. (a) Principal stresses; (b) Maximum principal stress orientation.
![]()
Figure 6. Stress distribution due to impact misalignment.
to the position on the circular test piece if viewed from the top. The magnitude of the stress is plotted on the radial axis. Gauges placed near the 270˚ position measure the highest stresses. This corresponds to the free end of the hammer assembly with the support being at the opposite end or the 90˚ position. Extrapolation of the stress distribution displays as a circle offset from the centre of the polar plot. From the extrapolated distribution, position and magnitude of the estimated maximum stress is calculated.
Mean results of the extrapolation over the 34 impacts are presented in Table 3. Extrapolations for both circular and faceted test pieces are shown. It is noteworthy that the ratio of maximum over minimum extrapolated
![]()
Table 3. Stress extrapolation due to impact misalignment.
stresses highlights large amounts of misalignment for some principal stresses. The ratio of maximum extrapolated over maximum measured stresses ![]() allows an estimation of stress increase due to misalignment. This is used later for fatigue damage calculations.
allows an estimation of stress increase due to misalignment. This is used later for fatigue damage calculations.
A notch at the weld root or toe creates a high stress concentration resulting in a steep stress gradient and possible stress singularity. Strain gauges on the other hand average the strain field across the measurement matrix and hence should be placed in regions of moderate stress gradients. To accommodate high stress gradients, the “hot spot” method recommended by the relevant design standard was employed [7] . The method uses two stress values, at 0.5 times the plate thickness and 1.5 times the plate thickness perpendicularly away from the weld notch. From these two stress values, stress to the weld notch is linearly extrapolated and it is named the hot spot stress. Obviously this extrapolation does not reflect the real stress at the notch, however it forms a comparison system to the S-N fatigue data formulated using the same method.
The hot spot stress can be formulated mathematically by linear extrapolation to the weld toe [7] :
![]() (11)
(11)
![]() (12)
(12)
where:
![]() Extrapolated hot spot stress,
Extrapolated hot spot stress,
![]() Stress measured at 0.5 times plate thickness perpendicularly away from the weld notch,
Stress measured at 0.5 times plate thickness perpendicularly away from the weld notch,
![]() Stress measured at 1.5 times plate thickness perpendicularly away from the weld notch.
Stress measured at 1.5 times plate thickness perpendicularly away from the weld notch.
This method was used to determine the hot spot stresses at the facet corner weld. Measurement points 1i and 1ii were placed at 0.5 and 1.5 times plate thickness perpendicularly away from the weld notch, respectively. In order to calculate the stress ratio ![]() as shown in Equation (12), two values from the measurement point at the same time must be used. The signals were very dynamic, with natural frequency ringing superimposed onto primary impact. The signal was therefore filtered to allow determination of the comparative peak stress values. Raw and filtered signal for a single impact are illustrated in Figure 7. Results over the 34 impacts were calculated and the mean values are presented in Table 4. It is a curious result since the maximum principal stress
as shown in Equation (12), two values from the measurement point at the same time must be used. The signals were very dynamic, with natural frequency ringing superimposed onto primary impact. The signal was therefore filtered to allow determination of the comparative peak stress values. Raw and filtered signal for a single impact are illustrated in Figure 7. Results over the 34 impacts were calculated and the mean values are presented in Table 4. It is a curious result since the maximum principal stress ![]() decreases towards the weld notch, possibly indicating superposition of positive and negative stresses with the negative stress rapidly increasing towards the corner weld notch.
decreases towards the weld notch, possibly indicating superposition of positive and negative stresses with the negative stress rapidly increasing towards the corner weld notch.
Typically stress cycles with tensile components produce crack initiation and propagation, leading to fatigue damage. Rare circumstances of crack propagation under compressive stress loading are documented [8] , however there is lack of information about the compressive stress components associated with S-N fatigue data used [7] . It has been decided to only focus on stress cycles with significant tensile stress component, hence narrowing the fatigue analysis down to maximum principal stresses![]() .
.
To calculate the fatigue damage which gives the most conservative value, the critical position with the largest stresses must be identified. The largest tensile stress occurs at the inner side of the facet corner of the faceted test piece. As for the circular test piece, the largest tensile stress occurs on the inside cylindrical surface.
The stress spectrum is complex, composed of the initial impact and the proceeding ringing. A way to deal with this is to use the “rainflow” counting method, which decomposes a complex stress spectrum into a series of
![]()
Figure 7. (a) Raw stress measurement; (b) Filtered stress measurement.
simple stress cycles [9] . This method was used to calculate the fatigue damage at four locations. Three were on the inside corner of the facet and correspond to measurement points 1i, 2i and 3i. The fourth position was on the inside surface of the circular test piece and corresponds to the measurement point R1i.
The stress spectrum at these four positions of interest is presented in Figure 8. Stresses at the faceted test piece measurement points 1i, 2i and 3i have been factored in line with the hot spot method and stress increase due to impact misalignment. Stress at the circular test piece measurement point R1i has been factored by the scaling constant (see Equations (9) & (10) and Table 2) and stress increase due to impact misalignment. The number of stress cycles has been extended to the anticipated 2000 hits for the full duration of the installation procedure.
The position 1i suffers the largest magnitude stress cycles since it is closest to the hammer impact zone. The stress range at the other positions 2i and 3i are somewhat smaller indicating more general loading throughout the length of the monopile. The stress range at the position R1i referring to circular cross section geometry, is smaller than at positions 2i and 3i which refer to the faceted corner geometry. This illustrates the stress concentration of the faceted as compared to the circular geometry. This result would also depend on the number of facets in the geometry, with fewer sides likely having a more adverse effect.
Miner’s summation was used to deal with variable amplitude fatigue damage [10] . This damage function defines failure due to variable amplitude loading by:
![]() (13)
(13)
In this failure criteria, ![]() represents the number of cycles to failure and
represents the number of cycles to failure and ![]() is the actual number of cycles spent at cyclic stress range
is the actual number of cycles spent at cyclic stress range![]() . The damage is summed for all stress ranges i.
. The damage is summed for all stress ranges i.![]() can be obtained from S-N
can be obtained from S-N
data provided by the reference [7] :
![]() (14)
(14)
where plate thickness t is taken into account. Other parameters are based on material and weld classification. The large scale monopile is to be manufactured from structural steel S235 or similar. The weld is classified based on the direction of the principal stress incurring the damage. In our case it is the maximum principal stress ![]() which acts in the direction parallel to the longitudinal welds and perpendicular to the circumferential welds of the structure. The perpendicular is more damaging than parallel stress loading, resulting in a reduced fatigue life. Therefore the analysis is performed for perpendicularly loaded circumferential welds. Parameters associating with this weld classification are presented in Table 5. The plate thickness t was presented previously in Table 1.
which acts in the direction parallel to the longitudinal welds and perpendicular to the circumferential welds of the structure. The perpendicular is more damaging than parallel stress loading, resulting in a reduced fatigue life. Therefore the analysis is performed for perpendicularly loaded circumferential welds. Parameters associating with this weld classification are presented in Table 5. The plate thickness t was presented previously in Table 1.
Applying the damage function to the stress range spectrum yields a measure of damage incurred due to the monopile installation procedure. The damage is expressed as the percentage of the total life used up. Results for the four positions 1i, 2i, 3i and R1i are presented in Table 6. The fatigue damage is below 1% and is larger for the faceted geometry.
As was noted previously, the stress spectrum of position 1i displays the largest stress ranges as compared to other positions, since the position 1i is closest to the hammer impact zone. However the damage at position 2i is similar to but slightly larger than damage at position 1i. This is counter intuitive but can be explained. There are 283 and 508 stress cycles between 25 - 90 MPa for positions 1i and 2i, respectively. There are also 34 and 0 stress cycles above 90 MPa for positions 1i and 2i, respectively. Therefore there are approximately twice as many medium level stress cycles at position 2i than at position 1i, which is shown to be more significant than the lack of a low number higher level stress cycles.
3. Conclusions
Piling trials were conducted to simulate a full scale monopile installation. Scaled down test pieces were used with the equipment representative of the full scale procedures. Two types of test pieces were used, conventional
circular and faceted. Both test pieces were instrumented with resistive strain gauges in attempt to quantify possible fatigue damage resulting from the full scale operation. It has been shown that the damage of the faceted geometry is larger than that experienced by the circular geometry but is still negligible in comparison with the full fatigue life available.
Fatigue damage calculations were based on the relevant design standard. The S-N data therein is general for a range of applications. Although the fatigue damage was shown to be negligible, there have been cases of monopile damage resulting from the piling installation. Therefore tests to failure may provide an understanding about the failure mechanisms and subsequent prediction of failure.
The approach used to link the test to the full scale conditions involved many scaling parameters. These parameters were estimated via dimensional analysis with stated assumptions. Strict validity of these scaling parameters should be investigated to gain more confidence in the results obtained.
There are currently no analytical or numerical models describing localised stressing of monopiles during the pile driving installation. This would require a 3D stress wave propagation model, perhaps implemented through the finite element method. Data gathered in this study can inform development of such a model; on the other hand, the model itself could shed light on various aspects of the test conducted, for example, the best measurement point placement in order to capture the most critical stressing of the welds. It could also provide a better understanding with regards to impact misalignment which will inform the relationship between nominal and peak stressing.
Acknowledgements
This work was performed in collaboration with TWI Ltd., Gardline, BSP International Foundations Ltd., Scottish Power Renewables, Tata Steel and OGN, with support from the Regional Growth Fund and Narec. The authors specifically acknowledge the support of TWI in producing the scaled down test piece and BSP for providing the facilities necessary to carry out the pile driving test.