Damage Characterization of Composite Structures Using Difference Peak Signal-to-Noise Ratio as a Function of Variable Wavelets (ΔPSNR-ΔW) ()
Received 23 March 2016; accepted 24 April 2016; published 28 April 2016

1. Introduction
Wavelet transform (WT) is a useful tool for image processing. It plays a critical role in many non-medical and medical applications. Data contained in an image are generally contaminated by noise or interfering signals, which can mask the actual data of interest. Furthermore noise can be caused by other means such as transmission errors and compression. Thus the noise removal is essential on many occasions before data in an image is analyzed reliably. The need is for an efficient and effective denoising algorithm to be used to recover data of interest without causing too many changes and artifacts to the image under consideration such as blurring.
Noise removal and reconstruction of original image is carried out through wavelet coefficients which are the result of decomposition in wavelet transform by eliminating the small coefficients normally associated with noise. The original image can be obtained by an algorithm using the noise free coefficients. Such reconstructed image is possible using a threshold function, which estimates noise levels.
The Wavelet Transform offers better image resolution employing orthogonal wavelet decomposition process. The overall process splits the approximation coefficients sub-band of the image into four sub-bands, thus obtaining a sub-band of coefficients (Approximate) and three sub-bands of detail coefficients (Horizontal, Vertical, Diagonal) as shown in Figure 1. Further transformations can be carried out by splitting the new approximation coefficient sub-band in a recursive way, where each detail coefficients sub-band is also decomposed into four sub-bands using the same approach as in approximation sub-band splitting. The Wavelet Transform for an image gives a large number of sub-bands of wavelet coefficients with different resolutions. The various decomposition levels can be correlated to such resolutions and tested using Peak Signal-to-Noise Ratio (PSNR) to measure each decomposition level effectiveness and hence can correlate all used levels to more accurately determine areas and levels of critical damage appearing within an image [1] - [6] .
In this paper component structural degradation is investigated in RIM composite samples using two powerful image investigation tools, namely WT and PSNR in a novel way. Search through and slicing algorithm of images representing components under inspection is a very important aiding technique in establishing damage level, however, to reduce testing time taken by the number of iterations and inspected layers of an image, Difference Peak Signal-to-Noise-Ration (∆PSNR) as a function of Wavelet Transform (WT) is used to narrow the domain of search and to highlight areas of damages more accurately. Such approach can show how degraded a known image becomes, indicating changes in the contents of the image. The new approach applies the combined algorithms under MATLAB environment to search through images of composite structures (images obtained through wavelength variation and RGB recombination).
2. Experimental Results
An analytical approach is used to first establish the most appropriate wavelet type maximum level of decomposition by employing 4 main types of wavelets with 5 levels of composition and applying them to a specific image layer for both S1 and S2 RIM composite samples. This is shown in Figures 2-9, where M is layer number and N is decomposition level. Table 1 shows initial observations regarding tried and tested wavelets. The MATLAB environment provided the simulation process. The examined images belong to RIM composite structures similar to materials used to produce artificial limbs. Such composites suffered different levels of controlled load impacts on the surface at angles π/2 and π/6.
3. Analysis and Discussion
From Figures 2-9 and Table 1, the following is realized:
![]()
Figure 1. Two levels wavelet transformation.
1) Wavelets such as DB20 and Dmey cause artifacts and mirror effect to the damage under evaluation and will result in data that will present the damage as amplified compared to its real and actual situation.
2) Higher levels of decomposition are desirable as it reveals more details of the damage level and spread.
3) wavelets that cause blurring such as Haar needs further analysis in correlation to damage type and decomposition level [7] - [12]
Figures 10-27 show searched through image for RIM composite that suffered impact damage in two places, one at angle π/2 and the other at angle π/6 While Figures 28-40 show searched through image for RIM composite that suffered fiber breakage and fiber extraction.
The new and novel approach is carried out as follows:
1) Each layer of the cycled image shown in Figures 10-40 is cycled through five times corresponding to the five levels of decomposition (N) and then PSNR is each time.
2) The process is carried twice for both Sym8 and Haar in order to establish both blurring effect and effect of number of decomposition levels on the accuracy of pinpointing damage area and level.
3) Difference PSNR (∆PSNR) is carried out with first decomposition level used as a reference. This is analogue to PSNR using a reference image when computed.
Figures 41-44 show both samples S1 and S2 tested using this approach.
From Figures 41-44, the following is evident:
1) S2 has suffered a more severe damage and fiber breakage, which is evident at decomposition levels 4 and 5 of Sym8 wavelet, where the characteristics show an inversion in the curve direction relating searched layers to ∆PSNR as a function of wavelet type and level, where S1 which is known to have suffered less damage show a continuous curve with no breaks or inversion at N = 4, N = 5.
2) For both S1 and S2 that suffered different levels of damage, Haar characteristics did not reveal a difference between them as shown in Figures 42-44. This is due to blurring effect at higher decomposition levels and was shown for S1 and S2 in Figures 3-7.
From Figures 41-44 and using the following expressions, it is now possible to accurately determine the layers of interest within an image and to establish a reference equation to compute damage level.
1) For S1 (Light Impact Damage―LID), the expressions are:
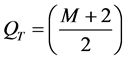 (1)
(1)
Transition layer from undamaged to damaged area within the sample.
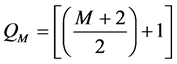 (2)
(2)
Exact layer at which the damaged area first noticed.
2) For S2 (Heavy Impact Damage―HID and fiber breakage), the expressions are:
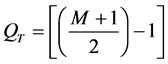 (3)
(3)
Transition layer from undamaged to damaged area within the sample.
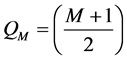 (4)
(4)
Exact layer at which the damaged area first noticed.
![]()
Figure 41. Damage detection in S1 using Sym8.
![]()
Figure 42. Damage detection in S1 using Haar.
![]()
Figure 43. Damage detection in S2 using Sym8.
![]()
Figure 44. Damage detection in S2 using Haar.
Equations (1) to (4) show the actual difference in behavior of an image search through algorithm, which will be used as input to the algorithm used here employing Difference PSNR and WT. The searched through images for S1 and S2 are shown previously in Figures 10-40. The overall algorithm will make use of Equations (1) to (4) and can be described using Equation (5) as below:
![]() (5)
(5)
where
![]()
The value of ![]() will correspond to layer numbers described in Equations (1) to (4) as defined in Equation 6:
will correspond to layer numbers described in Equations (1) to (4) as defined in Equation 6:
![]() (6)
(6)
From Figures 41-43, and applying Equations (1) to (6), the following is obtained and summarized in Table 2.
In the specific case of S1, there are two different areas of Impact damage at two different angles to the normal to the surface of the composite sample surface. Hence, Equation (7) and Equations (8) and (9) represent the layer
![]()
Table 2. Impact damage characteristics for vertical load drop.
delay in uncovering the second lighter damage on the surface of the same sample S1:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
In the case of Sample S1, and substituting the values for impact load incident angles, gives:
From Table 2 and Table 3, damage characteristic matrices (Ch) can be produced as follows:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
It is realized that:
1) The matrix values for S2 are more than twice the values obtained for S1. This further supports the observation of fiber breakage and fiber extraction and proves the validity of using higher levels of decomposition for selected Sym8 wavelet to detail such values.
2) Taking a sample from the previous image figures (Figure 21 and Figure 36), it is clear that S2 suffered more than twice the impact force, which resulted in fiber breakage and Damage 1 (D1) is S1 has suffered Almost twice the Value of impact compared to Damage (D2) which made contact with the composite sample at an angel π/6, with its Sin = 0.5. These observations are supported by the diameter of damaged area, as shown in Figure 45 and Figure 46.
3) The difference in the internal coloring of the damaged areas in S1 and S2 samples indicates the severity of damage in S2 compared to S1.
Using such algorithm that employs difference PSNR results in a reduction to the number of layers needed to be inspected closely and stored as an evidence of damaged structure. Also, it accurately points out the area or areas of damage. Also it correlate the severity of damage to both the number of inspected layers and the PSNR values expected for such level of damage [13] [14] .
4. Conclusions
It is evident from the presented work that:
1) The type of wavelet and level of decomposition have a marked effect on uncovering damage in composite structures when applied to obtained images, which also applies to medical image analysis.
![]()
Table 3. Impact damage characteristics for angled load drop.
![]()
Figure 45. Damaged areas diameter difference in S1.
2) ∆PSNR is an excellent approach to zooming on the magnitude of damage in a structure through application of PSNR to images.
3) ∆W is a good approach when combined with PSNR to reveal the scale of damage and also provides better details.
4) A definitive relationship is established between PSNR, number of searched layers in an image and level and angle of impact.
The overall work describes a new way to approach damage analysis of images for both medical and composite structures.
This work provided a new approach and technique to NDT. Such approach evaluates structures more accurately as it links the main principles of PSNR and WT into a single algorithm that is applied to uncover level and extent of damage. Such way of testing can be also used to evaluate material strength and ability to withstand impacts.