The Case against Dark Matter and Modified Gravity: Flat Rotation Curves Are a Rigorous Requirement in Rotating Self-Gravitating Newtonian Gaseous Discs ()
Received 19 February 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction
A large number of observations, mostly in the 21 cm emission line of neutral hydrogen, have firmly established that the rotation curves of spiral galaxy discs do not exhibit a Keplerian falloff; in fact, most of them remain flat or slightly increasing as far away from the centers as they can be observed [1] - [22] . The radial scales over which the neutral hydrogen discs can be observed reach out to ~100 kpc in the largest spiral galaxies and since the rotation curves remain flat, it was postulated by many researchers that some unseen extended mass distribution ought to exist all the way out to hundreds of kiloparsecs from the galaxy centers. Thus the Dark Matter Hypothesis was born, and soon the news leaked out to the rest of the physics community and intensive and extensive searches for dark matter particles and fields boomed into existence. On the other hand, some researchers who certainly felt uncomfortable with this new “aetherial” hypothesis proposed that Newtonian gravity should instead be modified at galactic scales and beyond, in order to solve the problem of the fast rotation of HI galaxy discs [23] - [33] .
The gas in spiral galaxies is distributed in centrally concentrated, vertically thin discs. For this reason, it was expected that the rotation curves had to turn over at some intermediate radius and begin a decline that would be indicative of the absence of substantial amounts of matter at large radii. This view about the luminous matter is nowadays considered so settled and clear that it has made its way into introductory Astronomy textbooks that compare and contrast the kinematics of spiral galaxies to the kinematics observed in our solar system (the Keplerian falloff mentioned above). In this work, we show that this elementary perception is quite naive and totally wrong because it ignores the influence (in fact, the dominance) of pressure and enthalpy gradients in self- gravitating gaseous discs. Personally, we believe that it amounts to a blunder because, before the results described below and even back in the 1980s when all this was unfolding, we had important clues that pointed out the importance of gas pressure in determining the equilibrium structures of gaseous discs. For instance, the sound-crossing time at 10 kpc in a 104 K cold galaxy disc is 1 Gyr, a value that lies to within 1.5 - 3 of the rotation timescales at 10 kpc in all galaxies with rotation speeds of 100 - 200 km∙s−1. Gallagher et al. [34] noted that the star formation histories of a sample of irregular and spiral galaxies did not indicate the presence of dark matter in the low-mass galaxies of the sample. But the most obvious clue was the existence of the Mestel disc [35] , a centrally concentrated potential-density pair with a flat rotation curve (see also [36] ). The Mestel disc has always been considered just a toy model [37] and the situation did not improve when Schulz [38] showed that the finite Mestel disc requires significantly less mass to produce the flat rotation curve. The main argument against the universal adoption of the Mestel disc has been the absence of a physical law or reason that would make galaxy discs assume this specific surface density profile and rotation law.
The above argument is not based on solid reasoning. When nature shows us that she has widely adopted a specific property (the flat rotation curves in galaxy discs), Aristotelian Logic dictates that we should search for a new law or reason, in order to understand the universality of this property and establish its physical meaning; not to create ghosts (particles and fields), aethers, and new forces that effectively facilitate our aversion to con- fronting the facts.
We do not claim that the Mestel disc [35] is the answer to establishing the universality of flat rotation curves in galaxy discs; only that it has always been a telling clue that gravity does not pull the strings and is not in control in gaseous self-gravitating discs. Furthermore, we have solved the full Newtonian problem and we now know precisely how such universal rotation curves emerge in spiral galaxy discs. The resolution of this ubiquitous problem is the subject of this paper. Before we can delve into the physics of the problem, we need to correct some common misconceptions that appear in the theory of second-order differential equations and which also have made their way into the textbooks. We do so in Section 2. Then, in Section 3, we revisit the theory of rotating Newtonian isothermal gaseous-disc equilibrium models and we calculate analytically the mean shapes of their density profiles and their rotation curves. The results match precisely the shapes of the rotation curves of spiral galaxy discs with no additional assumptions of any kind. So these results make a strong case against both dark matter and modified gravity and their implications have far-reaching consequences all the way to cos- mology. For completeness, we describe in Section 4 polytropic models that also demand monotonically increas- ing rotation curves because they are subject to the same physical principles. These models are also applicable to very young protoplanetary discs (certainly to pre-Class 0 discs and possibly to the youngest Class 0 non- Keplerian discs). Finally, we conclude with a discussion of all the pertinent issues and our results in Section 5.
2. Second-Order Differential Equations and the Cauchy Problem
In mathematical physics, the trivial solutions of the various second-order differential equations are commonly ignored as being uninteresting; and too much attention is paid to the Cauchy problem in determining arbitrary constants as opposed to the internal properties of the equations themselves that have no regard for externally im- posed conditions of any type. Both of these practices are damaging as they work to hinder our efforts toward solving the physical problems described by the differential equations in the first place. Such practices are rele- vant to all linear and nonlinear second-order equations of physics, so we can discuss and clarify the various issues involved by using any well-known equation. We choose to make use of the Bessel differential equation in this section.
The Bessel equation [39]
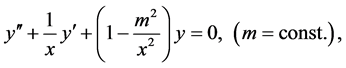 (1)
(1)
has regular solutions that are called Bessel functions of order m and a trivial solution . The trivial solution is not singular as it can be obtained from the regular solutions by an appropriate choice of the arbitrary constants. Nevertheless, its name indicates that y = 0 is of no interest at all. It is also well-known that the Bessel functions all oscillate about the x-axis [39] , but this statement is grossly inaccurate and obscures the truth: the regular solutions oscillate about the trivial solution which just happens to coincide with the x-axis in this case. We demonstrate this important point by solving numerically an inhomogeneous
. The trivial solution is not singular as it can be obtained from the regular solutions by an appropriate choice of the arbitrary constants. Nevertheless, its name indicates that y = 0 is of no interest at all. It is also well-known that the Bessel functions all oscillate about the x-axis [39] , but this statement is grossly inaccurate and obscures the truth: the regular solutions oscillate about the trivial solution which just happens to coincide with the x-axis in this case. We demonstrate this important point by solving numerically an inhomogeneous 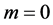 Bessel equation of the form
Bessel equation of the form
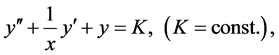 (2)
(2)
along with nonsingular boundary conditions that attempt to initially push the regular solutions away from the new trivial solutions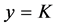 :
: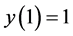 ,
, 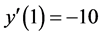 for K = 5; and
for K = 5; and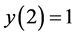 ,
, 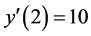 for
for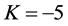 . The results are shown in Figure 1. Both regular solutions have nothing to do with the x-axis; instead, they turn around and settle into oscillations that clearly occur about the new trivial solutions
. The results are shown in Figure 1. Both regular solutions have nothing to do with the x-axis; instead, they turn around and settle into oscillations that clearly occur about the new trivial solutions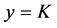 . This behaviour can be demonstrated for all linear second-order equations of mathematical physics with oscillatory regular solutions [40] and for (non)linear equations of the Lane-Emden type [41] - [45] . The lesson to be learned is that the so- called trivial solutions of second-order equations are not at all trivial. They are in fact favoured by the diffe- rential equations themselves which have no regard for the externally imposed boundary conditions. Thus, we will heretofore call these solutions the intrinsic solutions that are preferred and demanded by the equations themselves, irrespective of the externally imposed Cauchy problem.
. This behaviour can be demonstrated for all linear second-order equations of mathematical physics with oscillatory regular solutions [40] and for (non)linear equations of the Lane-Emden type [41] - [45] . The lesson to be learned is that the so- called trivial solutions of second-order equations are not at all trivial. They are in fact favoured by the diffe- rential equations themselves which have no regard for the externally imposed boundary conditions. Thus, we will heretofore call these solutions the intrinsic solutions that are preferred and demanded by the equations themselves, irrespective of the externally imposed Cauchy problem.
When the Cauchy problem is solved, as in Figure 1, the externally imposed boundary conditions are usually at odds with the underlying equation and the regular solutions cannot match the favoured intrinsic solution. As a result, the regular solutions are forced by the equation itself to oscillate about the intrinsic solution as soon as they intersect this favoured solution the first time. Thus, the intrinsic solutions act as attractors of the regular solutions which, in turn, are forced to always stay near and around the more dominant intrinsic solutions. We view this behaviour as a triumph of the differential equation (and its intrinsically favoured solution) over the Cauchy problem (and the particular solution it strives to produce).
This striking behaviour remains intact in at least some nonlinear second-order equations. Very clear examples in which rotation is involved can be found in [43] and [44] . Here we provide two additional nonlinear examples of the dominance of intrinsic solutions over regular solutions drawn from Lane-Emden equations [46] [47] in the absence of rotation. The isothermal Lane-Emden equations, take the form
 (3)
(3)
where D is the dimensionality of space (![]() in spherical coordinates and
in spherical coordinates and ![]() in cylindrical coordinates). Singular and regular solutions have been obtained in many applications [48] - [50] [37] [42] [44] and they are all nonoscillatory.1 The reason for this is quite obvious: Equation (3) does not have an intrinsic solution because
in cylindrical coordinates). Singular and regular solutions have been obtained in many applications [48] - [50] [37] [42] [44] and they are all nonoscillatory.1 The reason for this is quite obvious: Equation (3) does not have an intrinsic solution because![]() . Why the latter condition precludes an intrinsic solution will become clear in the next section, where we describe a procedure for obtaining intrinsic solutions.
. Why the latter condition precludes an intrinsic solution will become clear in the next section, where we describe a procedure for obtaining intrinsic solutions.
In stark contrast, the polytropic Lane-Emden equations, take the form
![]() (4)
(4)
where n > 0 is the polytropic index, and it possesses the intrinsic solution y = 0. Although few analytic solutions are known [50] [52] , numerical integrations show that, depending on n, this equation has both oscillatory and nonoscillatory solutions. For Equation (4), we have derived a precise criterion for the existence of oscillatory solutions [45] . This criterion predicts that for D = 2 (cylindrical form), all solutions with odd integer n-values are oscillatory; while for D = 3 (spherical form), only the ![]() and
and ![]() integer-n solutions are oscillatory. Numerical integrations (using the physical boundary conditions
integer-n solutions are oscillatory. Numerical integrations (using the physical boundary conditions![]() ,
,![]() ) easily confirm these results. The reason for the existence of nonoscillatory solutions is that for the corresponding choices of n, the differential equation is not a harmonic oscillator [40] . This is also true for the modified Bessel equation [39] that is known to possess only nonoscillatory solutions. Its real solutions cannot be oscillatory2 and they are then prohibited from intersecting the intrinsic solution
) easily confirm these results. The reason for the existence of nonoscillatory solutions is that for the corresponding choices of n, the differential equation is not a harmonic oscillator [40] . This is also true for the modified Bessel equation [39] that is known to possess only nonoscillatory solutions. Its real solutions cannot be oscillatory2 and they are then prohibited from intersecting the intrinsic solution ![]() more than once [40] .
more than once [40] .
3. Isothermal Self-Gravitating Newtonian Gaseous Discs
In what follows, we use the arbitrary scaling constants ![]() and
and ![]() to normalize the disc radius R and density
to normalize the disc radius R and density![]() , respectively. We thus define the dimensionless radius
, respectively. We thus define the dimensionless radius ![]() and density
and density![]() . Velo- cities
. Velo- cities ![]() are also normalized consistently by the constant
are also normalized consistently by the constant![]() , where G is the Newtonian gravitational constant, in which case we also define the dimensionless rotation velocity
, where G is the Newtonian gravitational constant, in which case we also define the dimensionless rotation velocity![]() . The same scaling also applies to the sound speed
. The same scaling also applies to the sound speed ![]() of the gas which in this section is a constant, i.e., the dimen- sionless sound speed is
of the gas which in this section is a constant, i.e., the dimen- sionless sound speed is![]() .
.
The cylindrical isothermal Lane-Emden equation [46] [47] with rotation can then be written in dimensionless form as
![]() (5)
(5)
This equation describes the radial (x) equilibrium of a rotating, self-gravitating, gaseous disc or cylinder in which the gas obeys the isothermal equation of state![]() , where p is the dimensionless pressure of the gas. Equation (5) is valid exactly for infinite cylinders and to a high degree of approximation in the equ- atorial (symmetry) planes of discs (see the Appendix). This latter point has been demonstrated convincingly by the calculations in [42] [53] [54] . In particular, the latter two investigations of finite discs uncovered equatorial density profiles that were strictly oscillatory under proper boundary conditions, just as was predicted by the analysis of Section 2 above.
, where p is the dimensionless pressure of the gas. Equation (5) is valid exactly for infinite cylinders and to a high degree of approximation in the equ- atorial (symmetry) planes of discs (see the Appendix). This latter point has been demonstrated convincingly by the calculations in [42] [53] [54] . In particular, the latter two investigations of finite discs uncovered equatorial density profiles that were strictly oscillatory under proper boundary conditions, just as was predicted by the analysis of Section 2 above.
Hayashi et al. [53] and Schmitz [55] studied also the stability of such equilibria and found that, except for the very flattened discs and the nearly spherical configurations, the intermediate models are stable. The very flattened discs in [53] , in particular, were unstable to ring formation that causes their equatorial power-law density profiles to become oscillatory, in agreement with the numerical solutions of Equation (5) obtained in [44] .
Despite the exact analytic results of the researchers quoted above, an objection has been raised over the years concerning the validity of using cylindrical coordinates to study axisymmetric, vertically thin discs rather than just infinite cylinders; and this is also the major sticking point for the present work, so it needs to be addressed in detail. We defer the analysis of the Lane-Emden equations for vertically thin discs to an Appendix because it is much easier to follow the derivations after the intrinsic analytic solution has been obtained for cylinders as follows.
Christodoulou & Kazanas [44] described a procedure for obtaining the intrinsic solution of Equation (5): If we equate the last two terms:
![]() (6)
(6)
then this is an intrinsic solution provided that the rest of the equation (the radial variation of the logarithmic gra- dient of the enthalpy) vanishes:
![]() (7)
(7)
Equations (6) and (7) form a system in which ![]() is totally dependent on
is totally dependent on![]() . First we solve Equation (7) to obtain the radial density profile:
. First we solve Equation (7) to obtain the radial density profile:
![]() (8)
(8)
and then we solve Equation (6) to determine the rotation curve of the intrinsic solution:
![]() (9)
(9)
where
![]() (10)
(10)
The solution contains 3 free parameters, the integration constants A, B, and k. Parameter B sets the vertical scale of the rotation curve![]() ; here we choose
; here we choose![]() . This choice can be made for
. This choice can be made for ![]() and it implies that the power-law density profile is cut off at an inner boundary
and it implies that the power-law density profile is cut off at an inner boundary![]() , where
, where ![]() drops to zero.
drops to zero.
Figures 2-4 show the shapes of the rotation curves obtained from Equations (9) and (10) for various choices of the constants A and k. The results are scale-invariant (a property of power-law density profiles), so the radial
scale is arbitrary. It is not surprising (see Section 3.1 below) that, in these Newtonian models, one sees most of the shapes of the “flat” rotation curves observed in spiral galaxies.
The only shapes missing from the figures are those of the few falling rotation curves shown in [18] . Appa- rently, in some compact galaxies, the above equilibrium profiles did not endure (the sound-crossing time at 30 kpc for ![]() is 3 Gyr, so it seems that there has been enough time to achieve equilibrium); perhaps because of interactions with nearby galaxies; or because the “external” gravity of the massive bulges eliminates the intrinsic solution (see Section 4.1 and footnote 4 below). But even in these objects, the falloff is slower than Keplerian which implies that gas pressure is still fighting to establish its own preferred profiles. This must be the
is 3 Gyr, so it seems that there has been enough time to achieve equilibrium); perhaps because of interactions with nearby galaxies; or because the “external” gravity of the massive bulges eliminates the intrinsic solution (see Section 4.1 and footnote 4 below). But even in these objects, the falloff is slower than Keplerian which implies that gas pressure is still fighting to establish its own preferred profiles. This must be the
![]()
Figure 4. As in Figure 2, but for![]() . Figures 2-4 show that the curves become flatter for steeper values of the power-law index k.
. Figures 2-4 show that the curves become flatter for steeper values of the power-law index k.
case since the intrinsic solutions are favoured by the equilibrium differential equation itself (see Section 2) in the absence of other external forces. In the two galaxies observed by Casertano & van Gorkom [18] , certain segments of the rotation curves are flat and that indicates to us that the radial self-gravitational equilibrium has fallen apart at some locations but not (yet) everywhere in these discs.
The above results can be summarized as follows: The derived density profiles are simple power laws in radius and the rotation curves are flat or slightly increasing at large radii (Equations (9) and (10)) irrespective of the value of the index k. Spiral galaxies have always been fitted with exponential density profiles, thus we do not know which values of k occur in nature. Galaxy profiles will have to be fitted again, but the payoff this time will be substantial: when k is determined from observations, the large-scale rotation curve (away from the center) will also be obtained independently from the velocity measurements. Thus, the observational results will be tested for consistency within the same data set in each case. This also holds true for protoplanetary discs in their early isothermal or adiabatic (see Section 4 below) phases; but first we need to find such purely self-gravitating discs in a pre-Class 0 YSO (Young Stellar Object) stage, and the 21 cm HI line in emission or absorption may give us a chance [56] .
3.1. Physical Interpretation
But how can such power-law density profiles produce and support flat or slowly increasing rotation curves? The problem has always been that the centrifugal force remains too high in the outer regions of the disc where New- tonian gravity weakens substantially. How do these equilibrium models get around this discrepancy? The answer to these questions was given in [44] and we repeat it here: The Lane-Emden Equation (5) is a second-order differential equation. As such, it respects but does not rely solely on force balance. (As will be readily seen in Equation (12) below, force balance is guaranteed by the way that the specific enthalpy of the gas is operating.) This second-order equation describes locally the detailed radial (![]() ) variation of the logarithmic gradients (
) variation of the logarithmic gradients (![]() ) of the potentials involved in the struggle to reach equilibrium. So, initially, it is the log-gradient of the enthalpy (with help from rotation) that sets out to oppose the log-gradient of the gravitational potential. This competition can be seen by rewriting Equation (5) in the form
) of the potentials involved in the struggle to reach equilibrium. So, initially, it is the log-gradient of the enthalpy (with help from rotation) that sets out to oppose the log-gradient of the gravitational potential. This competition can be seen by rewriting Equation (5) in the form
![]() (11)
(11)
where ![]() and
and ![]() are the dimensionless enthalpy per unit mass and the Newtonian self-gra- vitational potential, respectively. This equation is exact for cylinders and approximately valid for discs at large radii (
are the dimensionless enthalpy per unit mass and the Newtonian self-gra- vitational potential, respectively. This equation is exact for cylinders and approximately valid for discs at large radii (![]() ,
,![]() ), where the vertical (z) gradient of the vertical gravitational force
), where the vertical (z) gradient of the vertical gravitational force ![]() becomes small and can be neglected.
becomes small and can be neglected.
In that case, how and why does the average intrinsic solution (Equations (8) and (9)) come into existence? The answer to these questions is even more illuminating: The intrinsic solution was derived above by imposing two separate conditions, that the centrifugal force should match the gravitational force (see Equation (6) and the last two terms in Equation (11)):
![]() (12)
(12)
while, at the same time, the log-gradient of the enthalpy should retire from the competition by assuming a con- stant profile (see Equation (7) and the leading term in Equation (11)):
![]() (13)
(13)
This occurs only for a power-law density profile (Equation (8)) and for a specific rotation profile (Equations (9) and (10)), and these profiles become internal properties characteristic of the equilibrium disc or cylinder. Stated more simply, up until now people believed that rotation was not related to the structure of the equilibrium disc and that they could adopt any arbitrary rotation profile for gaseous self-gravitating discs. We see now that this is not true, the radial density and rotation profiles are strongly coupled and uniquely determined through the intrinsic solution discussed above.
The only surprise in this narrative is the unique way that the differential equation finds to promote and estab- lish the above intrinsic solution: rather than trying to simultaneously balance the variations of the three poten- tials involved at every single radius (not possible because the corresponding timescales vary widely at different radii), the disc assumes gradually a logarithmic specific-enthalpy profile determined from the solution of Equ- ation (13):
![]() (14)
(14)
So it is the thermodynamic potential ![]() of the gas that becomes logarithmic, and not the gravitational potential that people have been trying to make it so for nearly 50 years! Naturally, the disc establishes such a logarithmic profile because this law guarantees precise force balance (Equation (12)) at all of its equatorial radii. The action of
of the gas that becomes logarithmic, and not the gravitational potential that people have been trying to make it so for nearly 50 years! Naturally, the disc establishes such a logarithmic profile because this law guarantees precise force balance (Equation (12)) at all of its equatorial radii. The action of ![]() unfolds in the physical disc from inside-out over timescales of the order of the local sound-crossing time
unfolds in the physical disc from inside-out over timescales of the order of the local sound-crossing time![]() . So the global equilibrium becomes complete after a time
. So the global equilibrium becomes complete after a time![]() , where
, where ![]() is the outer radius of the disc.
is the outer radius of the disc.
We understand physically the preceding results in the following manner: Self-gravity is a long-range force (by Gauss’s law, the gravitational potential at radius x depends on the entire mass interior to x) and it cannot adjust its potential in the disc to effect local changes to the density distribution. In other words, the density is a source term in the Poisson equation that determines the gravitational potential, but not the other way around. In stark contrast, enthalpy is a local potential whose action depends only on the local behaviour of the pressure and the density of the disc. When ![]() assumes its logarithmic radial profile (Equation (14)), it dictates that the local density adjust according to the local log-gradient of the pressure
assumes its logarithmic radial profile (Equation (14)), it dictates that the local density adjust according to the local log-gradient of the pressure
![]() (15)
(15)
By doing that, the enthalpy uses the density in order to modify the sourcing of both the gravitational potential (via the Poisson equation![]() ) and the centrifugal potential (via Equation (6)). The result of this tactic is a rotation law that is entirely dependent on the distribution of the density/enthalpy (see Equation (6)) that does not feed back (v does not enter in Equation (7)). The rotation so produced is capable of balancing gravity at all radii all by itself (Equation (12)), and the enthalpy retires from the struggle for equilibrium (Equation (7)) having implicitly won the competition at every radius.
) and the centrifugal potential (via Equation (6)). The result of this tactic is a rotation law that is entirely dependent on the distribution of the density/enthalpy (see Equation (6)) that does not feed back (v does not enter in Equation (7)). The rotation so produced is capable of balancing gravity at all radii all by itself (Equation (12)), and the enthalpy retires from the struggle for equilibrium (Equation (7)) having implicitly won the competition at every radius.
It is important to keep in mind that the enthalpy wins the struggle because the two equations of the intrinsic equilibrium solution (Equations (6), (7) or Equations (12), (13)) and the Poisson equation (![]() ) do not allow for feedback loops and counter-sourcing by self-gravity or rotation. Thus, the state of rotation, the density profile, and the local self-gravity have all been manipulated unilaterally by the action of the enthalpy.
) do not allow for feedback loops and counter-sourcing by self-gravity or rotation. Thus, the state of rotation, the density profile, and the local self-gravity have all been manipulated unilaterally by the action of the enthalpy.
3.2. Concluding Remarks
The above equations give us a new probe into gaseous astrophysical disc systems (Equations (6) and (7)). For spiral galaxy discs, this probe ought to routinely confirm the above-described density-rotation coupling, as the observations already exist. At the same time, we are full of anticipation about what we can learn from the very early phases of purely self-gravitating protoplanetary discs (before the central protostars form and dominate the dynamics) for which the rotation curves have not been measured with accuracy yet, but the radial density profiles in Class 0 YSOs have been obtained [57] [58] . Our prediction, of course, is that, if found, such early discs (preferably earlier than Class 0) will be observed to have “flat” rotation curves.3
4. Polytropic Self-Gravitating Newtonian Gaseous Discs
The cylindrical polytropic Lane-Emden equation [46] [47] with rotation can be written in dimensionless form as
![]() (16)
(16)
where ![]() is the polytropic index and the dimensionless constant sound speed
is the polytropic index and the dimensionless constant sound speed ![]() was defined for
was defined for![]() . (In general, the square of the sound speed
. (In general, the square of the sound speed ![]() varies as
varies as ![]() across the medium.) This equation describes the radial (x) equilibrium of a rotating, self-gravitating, gaseous disc or cylinder in which the gas obeys a polytropic equation of state
across the medium.) This equation describes the radial (x) equilibrium of a rotating, self-gravitating, gaseous disc or cylinder in which the gas obeys a polytropic equation of state![]() . As in Section 3, Equation (16) is valid exactly for infinite cylinders and to a high degree of approximation in the equatorial (symmetry) planes of discs (see the Appendix). This latter point is supported by the calculations in [43] [63] [64] that studied also the stability of thin-disc and cylindrical equilibria and found large regions of the parameter space with stable models for all values of
. As in Section 3, Equation (16) is valid exactly for infinite cylinders and to a high degree of approximation in the equatorial (symmetry) planes of discs (see the Appendix). This latter point is supported by the calculations in [43] [63] [64] that studied also the stability of thin-disc and cylindrical equilibria and found large regions of the parameter space with stable models for all values of![]() ; and a sizeable region in which flattened discs with power-law density profiles were unstable to ring formation that causes their profiles to become oscillatory, just as was predicted by the analysis of Section 2 above.
; and a sizeable region in which flattened discs with power-law density profiles were unstable to ring formation that causes their profiles to become oscillatory, just as was predicted by the analysis of Section 2 above.
We repeat the procedure outlined in Section 3 in order to obtain the intrinsic solution of Equation (16): If we equate again the last two terms:
![]() (17)
(17)
then this is an intrinsic solution provided that the rest of the equation (the radial variation of the logarithmic gradient of the enthalpy) vanishes:
![]() (18)
(18)
Equations (17) and (18) form a system in which ![]() is totally dependent on
is totally dependent on![]() . First we solve Equ- ation (18) to obtain the radial density profile:
. First we solve Equ- ation (18) to obtain the radial density profile:
![]() (19)
(19)
and then we solve Equation (17) to determine the rotation curve of the intrinsic solution:
![]() (20)
(20)
where B is the integration constant, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (i.e.,
(i.e.,![]() ), and the upper incomplete gamma function is defined as
), and the upper incomplete gamma function is defined as
![]() (21)
(21)
The solution contains 4 free parameters, the integration constants A, B, k, and the polytropic index n. Para- meter B can adjust the vertical scale of the rotation curve![]() , but here we opted to use
, but here we opted to use ![]() in what follows. This choice is equivalent to the boundary condition that
in what follows. This choice is equivalent to the boundary condition that![]() .
.
Figures 5-8 show the shapes of the rotation curves obtained from Equation (20) for two polytropes with ![]() and
and ![]() and for various choices of the constants A and k. As in the isothermal case of Section 3, the rotation profiles are slowly increasing or flat with radius x. In this case however, we need to obey the condition
and for various choices of the constants A and k. As in the isothermal case of Section 3, the rotation profiles are slowly increasing or flat with radius x. In this case however, we need to obey the condition ![]() (
(![]() in Equation (21) and
in Equation (21) and ![]() in Equation (19)) in the calculation of the gamma function and so the rotation curves terminate when x reaches its maximum value where
in Equation (19)) in the calculation of the gamma function and so the rotation curves terminate when x reaches its maximum value where ![]() as well. Two basic trends are
as well. Two basic trends are
![]()
Figure 6. As in Figure 5, but for![]() . Figure 5 and Figure 6 show that, for fixed n, the curves rise more steeply for steeper values of the index k.
. Figure 5 and Figure 6 show that, for fixed n, the curves rise more steeply for steeper values of the index k.
![]()
Figure 7. Rotation curves of the intrinsic solution of the n = 3 polytropic Lane-Emden equation for![]() ,
, ![]() , and various values of A.
, and various values of A.
![]()
Figure 8. As in Figure 7, but for![]() . Figure 6 and Figure 8 show that, for fixed k, the curves become flatter for higher values of the polytropic index n.
. Figure 6 and Figure 8 show that, for fixed k, the curves become flatter for higher values of the polytropic index n.
noted in the figure captions as well: 1) for fixed n, the curves rise more steeply for steeper values of the index![]() ; and 2) for fixed k, the curves become flatter for higher values of the polytropic index
; and 2) for fixed k, the curves become flatter for higher values of the polytropic index![]() .
.
4.1. Physical Interpretation
The polytropic Lane-Emden equation with rotation and its intrinsic solution assume the exact same forms as in the isothermal case (Section 3.1) when the polytropic equation of state ![]() is used to introduce the specific enthalpy
is used to introduce the specific enthalpy![]() . Therefore, the fundamental equations discussed in Section 3.1 also apply to polytropic models with finite radial extent and the enthalpy plays the exact same role in manipulating the source terms of the gravitational potential and the rotational potential.
. Therefore, the fundamental equations discussed in Section 3.1 also apply to polytropic models with finite radial extent and the enthalpy plays the exact same role in manipulating the source terms of the gravitational potential and the rotational potential.
The fact that the thermodynamic potential ![]() operates locally in the exact same manner (i.e.,
operates locally in the exact same manner (i.e.,![]() ) in polytropic and isothermal equilibria helps us correct another common misconception: Since the time that the results of Hayashi et al. [53] came to light (they studied isothermal self-gravitating gaseous discs that oddly exhibited power-law radial density profiles and “flat” rotation curves in equilibrium), it has been often stated that isothermal disc models tend to exhibit flat rotation curves because they happen to have a “special” mass distribution (i.e., their specific angular momentum is proportional to the mass interior to radius x, or their mass grows linearly with x). This is not true. The above results show without a doubt that there are no special equili- brium models; and that the isothermal and the polytropic equilibria are both subject to the same fundamental physics at the local level, where the thermodynamic potential
) in polytropic and isothermal equilibria helps us correct another common misconception: Since the time that the results of Hayashi et al. [53] came to light (they studied isothermal self-gravitating gaseous discs that oddly exhibited power-law radial density profiles and “flat” rotation curves in equilibrium), it has been often stated that isothermal disc models tend to exhibit flat rotation curves because they happen to have a “special” mass distribution (i.e., their specific angular momentum is proportional to the mass interior to radius x, or their mass grows linearly with x). This is not true. The above results show without a doubt that there are no special equili- brium models; and that the isothermal and the polytropic equilibria are both subject to the same fundamental physics at the local level, where the thermodynamic potential ![]() operates and dominates when the only gravity it faces is the self-gravity of the disc. As for the validity of using the cylindrical coordinate system with its “special”
operates and dominates when the only gravity it faces is the self-gravity of the disc. As for the validity of using the cylindrical coordinate system with its “special” ![]() operator for discs, this issue is addressed in detail in the Appendix.
operator for discs, this issue is addressed in detail in the Appendix.
Furthermore, as we have seen above, a flat rotation curve does not imply and does not need a linearly increas- ing mass distribution. Even if the underlying density profile is decreasing in radius (as the light does in spiral galaxy discs), a rising rotation curve is a requirement in the equilibrium solutions derived in this section and in Section 3 so long as more mass is added incrementally with increasing radius (this is simply a restatement of Gauss’s law). Therefore, one can assume a constant mass-to-light ratio and build a Newtonian self-gravitating galaxy disc model with a declining mass distribution that will still be required to have a rising rotation curve provided that the disc may be thin, but not razor-thin; that ![]() on the equatorial plane; and that its volumetric density profile is a power law in radius x (see the Appendix).
on the equatorial plane; and that its volumetric density profile is a power law in radius x (see the Appendix).
4.2. Concluding Remarks
The polytropic intrinsic solution (Equations (17) and (18)) gives us a new probe into nonisothermal astro- physical disc systems. In particular, protoplanetary discs undergo various early phases of adiabatic evolution (figure 2 in [65] ). We predict that, if found, such discs will be observed to have the same fundamental characteristics (Equations (19) and (20)) irrespective of the polytropic index n appropriate for each adiabatic phase. In fact, observations of the density profiles, fitted with Equation (19), may be able to determine, not only the profile constants k and A, but also the value of n, thereby deriving the equation of state of the gas in- dependently from theoretical models. The only problem is that we need to find such systems very early in their development (see footnote 3 above), and this is a difficult task [56] [57] [66] .
5. Discussion
The intrinsic solutions are very much related to the so-called trivial solutions of differential equations [44] . We now understand that there are no trivial solutions; in fact such solutions of second-order equations are quite dominant (Section 2): in many cases of interest, knowing the trivial solution of an equation implies that we know the average behaviour of all the regular solutions that depend on various types of boundary conditions but, nevertheless, end up oscillating about the intrinsic solution, provided that the differential equation is a harmonic oscillator (as the ordinary Bessel equations in Section 2; the nonisothermal Lane-Emden equations without rotation in Section 2; and the Lane-Emden equations with rotation in Sections 3 and 4).
The mean density and rotation profiles that we have derived analytically in Sections 3 and 4 are dominated by natural logarithms and power laws. This is the implicit reason that Marr [67] has recently suceeded in matching the shapes of the rotation curves of a sample of 37 spiral galaxies by using the log-normal probability distri- bution (and no dark matter or modified gravity) to describe the density profiles in the equatorial planes of the discs. This surface density distribution (Equation (2) in [67] ) is equivalent to a variable power law of the form ![]() in normalized radius x in which the index
in normalized radius x in which the index ![]() varies slowly across the disc as
varies slowly across the disc as
![]() (22)
(22)
where ![]() is the variance of the distribution, a free parameter to be fitted for each spiral galaxy model. In principle, a slowly varying
is the variance of the distribution, a free parameter to be fitted for each spiral galaxy model. In principle, a slowly varying ![]() is permitted by our analytic solution because the specific enthalpy
is permitted by our analytic solution because the specific enthalpy ![]() is a strictly local potential function (Equation (13) in Section 3.1); and if the power-law index k has to vary radially in order for the equilibrium disc to obey some other fundamental law (e.g., as Marr states, the total entropy of the overall configuration should be maximized), then such adjustment may occur on timescales determined by the local sound speed.
is a strictly local potential function (Equation (13) in Section 3.1); and if the power-law index k has to vary radially in order for the equilibrium disc to obey some other fundamental law (e.g., as Marr states, the total entropy of the overall configuration should be maximized), then such adjustment may occur on timescales determined by the local sound speed.
Our results render the Dark Matter Hypothesis unnecessary on galaxy scales. This removes the largest pillar of this hypothesis (flat rotation curves have remained to this day the “strongest piece of evidence” in favour of dark matter, but not any longer). But this “aetherial” hypothesis is not about to roll over and die without a fight. The next areas of confrontation will be larger than galaxy scales and cosmology. We are very much encouraged from a recent report of the absence of dark matter on larger than galaxy-disc scales: Magain & Chantry [69] analyzed 25 gravitational lenses and found that their mass determinations indicate the absence of extended dark matter haloes all the way out to distances comparable to the Einstein ring (the separation between lensed quasar images).
On the other hand, we do not anticipate any serious problems materializing in cosmology because we do not believe that there currently is any credible observational evidence in favour of dark matter or modified gravity on those largest scales. In fact, some results that argue against the necessity for dark matter on various scales have timidly begun to appear [70] - [76] . For these reasons, here is how we approach the issue of dark matter now: Christiaan Huygens presented his theory of elastic longitudinal light waves propagating in “aether” to the Paris Academy of Sciences in 1678 and published his views a few years later [77] . That year, the physics world entered a Dark Age that lasted nearly 200 years, until the genious of Michelson & Morley [78] finally showed that the universe is not filled with aether. It seems that we also live in another Dark Age, the “Dark Matter Dark Age”, that commenced in the 1970s when K. C. Freeman [1] and others [2] - [22] reported that the rotation curves of spiral galaxies were not falling with radius. By all accounts, the current Dark Age has lasted for nearly 50 years; and the sooner we get out of it, the better for our understanding of the large scales of the universe around us.
The analytic solutions that we have derived in this work should also find applications in the field of proto- planetary disc research (Sections 3.2 and 4.2), especially if very young, purely self-gravitating discs could be found in the future [56] . At present, only observations of Class 0 YSOs are widely available [57] [58] , but these systems are not young enough and do not have flat rotation curves; their protostars have formed and they are changing the dynamics and kinematics of the discs.4 We are encouraged however by the report of Tsitali et al. [66] who discovered a rising rotation curve in the inner 2000-8000 AU of the “first hydrostatic core” candidate Cha-MMS1.
Acknowledgements
We thank Joel Tohline for feedback and guidance over many years; and John Marr, Hsi-Wei Yen, and Earl Schulz for many fruitful discussions, especially those concerning the observations of astrophysical self-gravitat- ing discs.
Appendix: Vertically Thin Discs Versus Infinite Cylinders
When applied to the equatorial planes (![]() ) of thin discs, Equations (5) and (16) do not include the specific enthalpy term
) of thin discs, Equations (5) and (16) do not include the specific enthalpy term
![]() (23)
(23)
where![]() . This term is small for cold gases since it scales as the sound speed squared
. This term is small for cold gases since it scales as the sound speed squared![]() . Nevertheless, strong objections have been raised about the validity of this approximation. Here we address such objections as follows.
. Nevertheless, strong objections have been raised about the validity of this approximation. Here we address such objections as follows.
The analysis presented in Sections 3 and 4 shows that the specific enthalpy in cylinders assumes a logarithmic radial profile (Equation (14)). Now, pressure is an isotropic force and its nature is to push spherically out in self- gravitating gases. Therefore, Equation (14) suggests that, in axisymmetry, the specific enthalpy of the gas could assume the spherical form
![]() (24)
(24)
where r is the spherical radius normalized by![]() . Such behaviour is suppressed in cylinders by dropping the dependence on z from the equations. But, in principle, it should not be suppressed off-hand in discs, so the influence of the terms (23) and (24) should at least be quantified in the equatorial planes of discs:
. Such behaviour is suppressed in cylinders by dropping the dependence on z from the equations. But, in principle, it should not be suppressed off-hand in discs, so the influence of the terms (23) and (24) should at least be quantified in the equatorial planes of discs:
1) Applying the radial (x) component of the cylindrical Laplacian to Equation (24) and then setting![]() , we confirm Equation (14); that is, this term of the Lane-Emden equations vanishes on the equatorial plane, as was also found in the intrinsic solutions of Sections 3 and 4.
, we confirm Equation (14); that is, this term of the Lane-Emden equations vanishes on the equatorial plane, as was also found in the intrinsic solutions of Sections 3 and 4.
2) Taking the derivative with respect to z in Equation (24) and then setting![]() , we obtain the correct symmetry condition that
, we obtain the correct symmetry condition that ![]() on the equatorial plane of the disc. Then, using the equation for vertical hydrostatic balance,
on the equatorial plane of the disc. Then, using the equation for vertical hydrostatic balance, ![]() , we also obtain the correct boundary condition for the self-gravita- tional potential, that is
, we also obtain the correct boundary condition for the self-gravita- tional potential, that is ![]() at
at![]() .
.
3) Combining Equations (23) and (24), we find that
![]() (25)
(25)
This is the term that was ignored for discs in the radial force balance described by Equation (12). But it makes only a minor contribution to the force balance over all radii where![]() . Specifically, it modifies Equ- ations (6) and (17) to
. Specifically, it modifies Equ- ations (6) and (17) to
![]() (26)
(26)
where ![]() is a proportionality constant of order
is a proportionality constant of order![]() . For our models,
. For our models, ![]() for isothermal discs and
for isothermal discs and ![]() for polytropic discs. Since
for polytropic discs. Since ![]() (because
(because![]() ), the last term in Equation (26) opposes self- gravity. By integration of this equation, we find that its contribution to the rotation profile
), the last term in Equation (26) opposes self- gravity. By integration of this equation, we find that its contribution to the rotation profile ![]() is logarith- mic:
is logarith- mic:
![]() (27)
(27)
where B is the integration constant. We see now that the dimensionless mass per unit length
![]() (28)
(28)
makes the largest contribution to the rotation curve. Neglecting the term![]() , we can write
, we can write
![]() (29)
(29)
For ![]() (i.e.,
(i.e.,![]() ) and
) and![]() , this equation reduces to the cylindrical Gauss’s law applied onto the equatorial plane of the disc in the limit of
, this equation reduces to the cylindrical Gauss’s law applied onto the equatorial plane of the disc in the limit of![]() . This result differs conclusively from the con- ventional thinking that is responsible for the acceptance of dark matter in galaxies; that
. This result differs conclusively from the con- ventional thinking that is responsible for the acceptance of dark matter in galaxies; that![]() , thus a constant v requires
, thus a constant v requires![]() . Odd as it may seem, Equation (29) makes sense for discs because their equatorial planes do possess cylindrical symmetry in the limit of
. Odd as it may seem, Equation (29) makes sense for discs because their equatorial planes do possess cylindrical symmetry in the limit of![]() , no matter which coordinate system is used. For this reason, Equation (27) can also be derived by using the Laplacian in spherical coordinates in the limit of
, no matter which coordinate system is used. For this reason, Equation (27) can also be derived by using the Laplacian in spherical coordinates in the limit of![]() ,
, ![]() , and for
, and for![]() , where the inertial terms of the two coordinate systems become unimportant.
, where the inertial terms of the two coordinate systems become unimportant.
Similar results can also be obtained for Equations (3) and (4) in which the inertial terms ![]() for
for ![]() in both coordinate systems with
in both coordinate systems with ![]() and
and![]() ; and from some of the finite razor-thin disc/ring models of Huré et al. [79] with power-law indices
; and from some of the finite razor-thin disc/ring models of Huré et al. [79] with power-law indices ![]() (their Figure 4) in which the rotation curves can be calculated and turn out to be slowly increasing functions of radius. For power-law indices
(their Figure 4) in which the rotation curves can be calculated and turn out to be slowly increasing functions of radius. For power-law indices![]() , edge effects become important and blur the picture. But in the absence of radial boundaries, the infinitely extended discs show a self-similar power-law potential (their Equation (66)) capable of generating flat and slowly increasing rotation curves for shallow surface density profiles. These models support our results because the radial dis- tribution of their equatorial surface densities is a shallow power law that places sufficient mass at all radii to keep the rotation curves rising.
, edge effects become important and blur the picture. But in the absence of radial boundaries, the infinitely extended discs show a self-similar power-law potential (their Equation (66)) capable of generating flat and slowly increasing rotation curves for shallow surface density profiles. These models support our results because the radial dis- tribution of their equatorial surface densities is a shallow power law that places sufficient mass at all radii to keep the rotation curves rising.
On the other hand, the models in [79] with steep power-law surface densities (![]() ) exhibit falling rotation curves. This observation helps us understand a problem that plagues such two-dimensional models and that has been summarized in [37] . In all of these models, the surface densiy profiles were obtained by collapsing spheroi- dal homoeoids down to an equatorial plane. Then, when the surface densities decline steeply with radius x, there is not enough mass interior to x at large radii to cause the rotation curves to continue rising with radius. This is because some of the interior mass comes from homoeoids exterior to x and this mass does not attract at x. The Mestel disc [35] [79] [38] is the marginal collapsed model among all classical potential-surface density pairs in which all mass interior to x attracts, while the exterior mass does not contribute to radius x. So this model has barely enough mass at all radii to maintain a flat rotation curve. This explains also the peculiar property of the Mestel disc [35] to be the only two-dimensional model that obeys the cylindrical Gauss’s law at
) exhibit falling rotation curves. This observation helps us understand a problem that plagues such two-dimensional models and that has been summarized in [37] . In all of these models, the surface densiy profiles were obtained by collapsing spheroi- dal homoeoids down to an equatorial plane. Then, when the surface densities decline steeply with radius x, there is not enough mass interior to x at large radii to cause the rotation curves to continue rising with radius. This is because some of the interior mass comes from homoeoids exterior to x and this mass does not attract at x. The Mestel disc [35] [79] [38] is the marginal collapsed model among all classical potential-surface density pairs in which all mass interior to x attracts, while the exterior mass does not contribute to radius x. So this model has barely enough mass at all radii to maintain a flat rotation curve. This explains also the peculiar property of the Mestel disc [35] to be the only two-dimensional model that obeys the cylindrical Gauss’s law at ![]() for every radius R [37] :
for every radius R [37] :
![]() (30)
(30)
where ![]() is the mass enclosed within radius R and
is the mass enclosed within radius R and ![]() is the self-gravitational potential.
is the self-gravitational potential.
We argue that all other razor-thin models that do not satisfy Gauss’s law at ![]() are physically question- able. This is because the homoeoids from which they were constructed do satisfy Gauss’s law over similar Gaussian surfaces. Our models do not suffer from such questionable behaviour because they follow the three- dimensional density distribution
are physically question- able. This is because the homoeoids from which they were constructed do satisfy Gauss’s law over similar Gaussian surfaces. Our models do not suffer from such questionable behaviour because they follow the three- dimensional density distribution ![]() in the equatorial plane of a thin (or thick) disc; and these models obey Gauss’s law at every radius R in the limit of
in the equatorial plane of a thin (or thick) disc; and these models obey Gauss’s law at every radius R in the limit of ![]() for a Gaussian surface that matches their symmetry (an infinitesimally tall cylindrical surface of radius R).
for a Gaussian surface that matches their symmetry (an infinitesimally tall cylindrical surface of radius R).
Rising rotation curves were also found by Marr [67] who studied models in which 1/x surface density profiles were truncated at a radius near the last observed point. By not being there to pull outward, the exterior mass allowed the inward force due to the interior mass to amplify, and this caused the rotation curves to turn up near the peripheries of the discs, despite the fact that these were essentially Mestel discs. In any case, our analytic solutions (Sections 3 and 4) avoid the above pitfalls (mixing of homoeoids of different sizes, truncation creating sharp edges); and they show that the volumetric density at all equatorial radii is always sufficient to continue pulling the rotation curves higher.
For ![]() in Equation (29), the term
in Equation (29), the term ![]() determines the rotation curves of the models. Hidden in this term are the two different types of Newtonian models that we have discovered and that require monotonically rising (not flat) rotation curves in discs and cylinders:
determines the rotation curves of the models. Hidden in this term are the two different types of Newtonian models that we have discovered and that require monotonically rising (not flat) rotation curves in discs and cylinders:
1) In all isothermal models with ![]() and in all polytropic models (Figures 5-8), the indefinite integral in
and in all polytropic models (Figures 5-8), the indefinite integral in
Equation (27) is positive definite. Then ![]() implying that
implying that![]() ,
, ![]() , and the rotation
, and the rotation
curves rise at all radii as more interior mass is added incrementally by the radial integration with increasing x.
2) On the other hand, in the isothermal models with ![]() (Figure 3 and Figure 4), the indefinite intergal in Equation (27) is negative definite (although the integral for the mass is still positive). Then, in effect,
(Figure 3 and Figure 4), the indefinite intergal in Equation (27) is negative definite (although the integral for the mass is still positive). Then, in effect, ![]() (where now it is necessary that
(where now it is necessary that![]() ), and the rotation curves approach asymptotically the constant value
), and the rotation curves approach asymptotically the constant value ![]() as
as ![]() decreases toward zero with increasing x. Because
decreases toward zero with increasing x. Because ![]() is a very steeply decreasing function of x in such cases, then
is a very steeply decreasing function of x in such cases, then ![]() from below quite fast, and that makes the rotation curves appear quite flat over most radii in Figure 3 and Figure 4. Here,
from below quite fast, and that makes the rotation curves appear quite flat over most radii in Figure 3 and Figure 4. Here, ![]() implies the inner boundary condition that
implies the inner boundary condition that ![]() at a cutoff radius
at a cutoff radius![]() .
.
Returning to the pressure term (![]() ) in Equation (27), if it is included in
) in Equation (27), if it is included in ![]() in future models, this term has the potential to drive some rotation curves down at large radii because it is negative for
in future models, this term has the potential to drive some rotation curves down at large radii because it is negative for ![]() (since
(since![]() ). This behaviour can occur only in discs since this term is not present in infinite cylinders. So, unlike discs, cylindrical star-forming filaments [80] [81] can never exhibit falling rotation curves in equilibrium; except for the unlikely case that their age would be smaller than the sound-crossing time, a sign of extreme youth indicating that a global equilibrium has not been established yet.
). This behaviour can occur only in discs since this term is not present in infinite cylinders. So, unlike discs, cylindrical star-forming filaments [80] [81] can never exhibit falling rotation curves in equilibrium; except for the unlikely case that their age would be smaller than the sound-crossing time, a sign of extreme youth indicating that a global equilibrium has not been established yet.
Our analysis in Sections 3 and 4 was carried out without the ![]() term of Equation (27) in order to bring out the physics of such Newtonian systems. Nevertheless, the pressure term in Equation (27) or some similar approximation may be of interest to researchers planning to remodel the rotation curves of spiral galaxies. But it does not appear to be necessary to modeling the rotation of pre-Class 0 protoplanetary discs because such starless discs are subject to extended infall of matter [58] that ought to create cylindrical, vertically thick quasi- equilibria to a good approximation.
term of Equation (27) in order to bring out the physics of such Newtonian systems. Nevertheless, the pressure term in Equation (27) or some similar approximation may be of interest to researchers planning to remodel the rotation curves of spiral galaxies. But it does not appear to be necessary to modeling the rotation of pre-Class 0 protoplanetary discs because such starless discs are subject to extended infall of matter [58] that ought to create cylindrical, vertically thick quasi- equilibria to a good approximation.
NOTES
1The periodic solution found in [51] describes a Cartesian slab and not a disc or cylinder.
2We note in passing that, as a result of the substitution ![]() that produces the modified Bessel equation [39] , its solutions are oscillatory about the imaginary axis in the complex plane.
that produces the modified Bessel equation [39] , its solutions are oscillatory about the imaginary axis in the complex plane.
![]()
3In the case of the Class 0 young system L1527 [59] [60] , the rotation curve is not flat, but we did not catch this 0.3 Myr old system early enough (the sound-crossing time at 100 AU for a 10 K cold gas with Co = 0.3 km∙s−1 is 1500 yr). On the other hand, Yen et al. [61] [62] report several other Class 0 YSOs whose rotation is not Keplerian outside of the inner few AU.
![]()
4When a protostar grows at the center of a protoplanetary disc, the enthalpy is defeated by gravity because the enthalpy cannot source and manipulate this component of the gravitational field via the Poisson equation (see Section 3.1); and the intrinsic solutions described in this work are no longer valid for such gaseous discs subject to “external” gravitational fields.