Comparison of Two Sample Tests Using Both Relative Efficiency and Power of Test ()
Received 1 February 2016; accepted 24 April 2016; published 27 April 2016

1. Introduction
One of the challenges faced by researchers most especially, statisticians, is to take decisions in the presence of uncertainties. Most often, intelligent guess is made and statistical methods are applied to validate or reject any possible assumptions that might have been made to enable the use of such methods. Numerous methods exist for testing statistical hypotheses in various conditions. In some cases, the probability distribution of the population from which samples are drawn is known. For instance, if the population is assumed to be normal; then, the sample size is assumed to be sufficiently large to justify the assumption of normality. In special cases, the sample sizes are very small and the probability distribution of the populations from which samples are drawn is unknown; hence, the sample is said to be distribution free and only non-parametric methods are applied. Thus, in most cases where the assumption of parametric methods is violated or not met, the non-parametric methods are usually preferred. Non-parametric methods that readily suggest themselves include the Median and the Mann- Whitney U test [1] . These methods require that the populations from which the samples are drawn to be continuous so that the probability of obtaining tied observations is at least theoretically zero [2] . Statistical tests could be for either paired or unpaired. In a paired test (Matched sample test), the data are collected from subjects measured at two different points wherein each subject has two measurements which are done before and after the treatment. Unpaired test on the other hand is when data are collected from two different and independent subjects. The size of the two samples may be equal or not, depending on the requirement of the test statistic. Techniques or methods for performing two sample tests abound but the question is “which method(s) perform better and under what conditions do they perform better when dealing with independent samples?” To make an articulate attempt to answer these questions, there is a need for proper and adequate comparative study of similar methods that can be used for the purpose of interest. The methods/techniques are: median test, modified median test intrinsically adjusted for ties, Mann-Whitney U test and modified intrinsically ties adjusted Mann-Whitney U test. All the above listed methods are for test of significant difference between variables/subjects when having independent samples. Wide comparison would expose researchers to conditions under which the methods are used to prevent type I or type II errors. In statistical computation, test statistics sometimes are affected by nature of data; that is, the distribution of the data which could be either symmetric or asymmetric in nature. In the determination of more effective statistical method, not just the null hypothesis should be of paramount interest but also the alternative hypothesis which implies that power of test plays an important role in the determination of effectiveness of statistical methods. The maximum value of power of test is 1 and the least is zero which is non- negativity property. The higher the power of test, the better the method and the lower the value, the less effective the method. In this paper, methods of analyzing two independent samples drawn from independent populations would be considered by subjecting some set of data to different conditions, such as sample size, to determine the condition under which they perform optimally in terms of Relative Efficiency (R.E) and power. The power efficiency of median test decreases as the sample sizes increases reaching an eventual asymptotic efficiency of 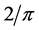 [3] . The modified median test intrinsically adjusted for ties was compared with the existing technique, ordinary median test; and the conclusion was that the modified median test intrinsically adjusted for ties easily enables the isolation of tied observations and estimation of their probability of occurrence [2] .
[3] . The modified median test intrinsically adjusted for ties was compared with the existing technique, ordinary median test; and the conclusion was that the modified median test intrinsically adjusted for ties easily enables the isolation of tied observations and estimation of their probability of occurrence [2] .
2. Material and Methodology
(1) MEDIAN TEST: Median test is a procedure for testing whether two independent groups (samples) differ in central tendencies represented by the population median [4] . The null hypothesis is
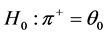 Vs
Vs 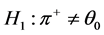 (1)
(1)
where 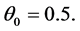
The test statistic is
 (2)
(2)
which under  becomes
becomes
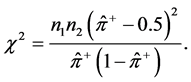 (3)
(3)
Reject 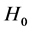 at α-level of significance if
at α-level of significance if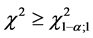 , otherwise, accept.
, otherwise, accept.
(2) Modified median test intrinsically adjusted for ties is used for test of equality in population media [2] .
The null hypothesis 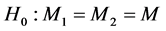 is equivalent to the null hypothesis,
is equivalent to the null hypothesis,
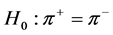 or
or  (4)
(4)

The test statistic is
 (5)
(5)
where
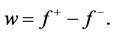
m is sample size of variable X.
n is sample size of variable Y.
![]() are respectively the probabilities that observations or scores by subjects from population X are on the average greater than , equal to, or less than observations or score by subjects from population Y.
are respectively the probabilities that observations or scores by subjects from population X are on the average greater than , equal to, or less than observations or score by subjects from population Y.
![]() are respectively the number of 1’s, 0’s and −1’s in the frequency distribution of these mn values of
are respectively the number of 1’s, 0’s and −1’s in the frequency distribution of these mn values of![]() .
.
Reject H0 at α-level of significance if![]() , otherwise, accept.
, otherwise, accept.
(3) Mann-Whitney U test is used for determination of the likelihood that two samples/groups emanated from the same population/distribution [5] .
The test statistic is
![]() (6)
(6)
Then,
![]() (7)
(7)
where
n1 is the total number of the first group/observation.
n2 is the total number of the first group/observation.
R1 is the sum of the ranks for the first group/observation.
Then
![]() (8)
(8)
is the mean and
![]() (9)
(9)
is the standard deviation.
This Z-score is, as usual, compared at a given level of significance with an appropriate critical value obtained from a normal distribution table for a rejection or acceptance of the null hypothesis.
(4) Modified Intrinsically Ties Adjusted Mann-Whitney U test is used to check whether two samples could have been drawn from the same population/distribution [6] .
The test statistic is
![]() (10)
(10)
where
n1 is the sample size of variable![]() .
.
n2 is the sample size of variable![]() .
.
R1 and R2 are the respectively sums of the ranks assigned to observations from populations ![]() and
and ![]() in the combined ranking of these observations from the two populations.
in the combined ranking of these observations from the two populations.
![]() ,
, ![]() are respectively the probabilities that observations or scores by subject from population X1 is on the average greater than or less than observations or scores by subject from population X2.
are respectively the probabilities that observations or scores by subject from population X1 is on the average greater than or less than observations or scores by subject from population X2.
The test hypothesis will be
![]()
vs
![]() .
.
Reject H0 at α-level of significance if![]() ; otherwise, accept.
; otherwise, accept.
Relative Efficiency of two test statistics (R.E) is the ratio of the variances of one of the two test statistics to the other (say: ![]() to
to![]() ) for equal sample size n. That is, relative efficiency of test
) for equal sample size n. That is, relative efficiency of test ![]() to
to ![]() is defined as
is defined as
![]() . (11)
. (11)
Between test 1 and test 2, test 2 is relatively more efficient than test 1 if the relative efficiency of the tests, ![]() is at least unity; that is if
is at least unity; that is if ![]() and hence test
and hence test ![]() is said to be more powerful than test
is said to be more powerful than test![]() .
.
Power of a statistical test is the probability of rejecting the null hypothesis when it is in fact false and should be rejected (i.e. the probability of not committing a type II error [7] . In other words, the power of test is equal to![]() , which is also known as the sensitivity [8] ; where
, which is also known as the sensitivity [8] ; where ![]() is the probability of committing type II error = error rate. Error rate is defined as the ratio of number of erroneous decision to number of replicate. That is;
is the probability of committing type II error = error rate. Error rate is defined as the ratio of number of erroneous decision to number of replicate. That is;
![]() .
.
In this paper, Monte Carlo’s Simulation techniques was used in the generation of data of different distributions and varying sample sizes ranging from 5 to 100 which was repeated 30 times for each sample size. In the simulation, sample size of 5, 10, 50 and 100 were considered to cover both small and large sample sizes. Monte Carlo simulation is defined as a method to generate random sample data based on some known distribution for numerical experiments. Monte Carlo simulation is an algorithm used to determine performance of an estimator or test statistic under various scenarios [9] .
3. Algorithm for Monte Carlo Simulation
1) Specify the data generation process.
2) Choose a sample size N for the MC simulation.
3) Choose the number of times to repeat the MC Simulation.
4) Generate a randomsample of size N based on the data generation process.
5) Using random sample generated in 4 above, calculate the test statistic(s).
6) Go backto (4) and (5) until desirable replicate is achieved.
7) Examine parameter estimates, test statistics, etc.
In the paper, for data from a known family of distributions, Gamma (4, 0.3) and Beta (2, 2) were used.
4. Result
From the simulated data using Monte Carlo simulation approach, the following results were obtained: Tables 1-4 are test statistics value of asymmetric distribution for different sample size while Tables 5-8 are test statistics value of symmetric distribution for different sample size. Table 9 is the variance of the test statistic considered. Table 9 is calculated from Tables 1-8.
Variances were computed from Table 1, Table 2, to Table 8.
![]()
Table 1. Test statistic value of sample size 5.
![]()
Table 2. Test statistic value of sample size 10.
![]()
Table 3. Test statistic value of sample size 50.
![]()
Table 4. Test statistic value of sample size 100.
![]()
Table 5. Test statistic value of sample size 5.
![]()
Table 6. Test statistic value of sample size 10.
![]()
Table 7. Test statistic value of sample size 50.
![]()
Table 8. Test statistic value of sample size 100.
![]()
Table 9. Variances of the test statistic considered.
As shown in Table 10, M1 to M4 are the methods considered as M1 is the Median test and M2 is Modified Median test (MMED), M3 is the Mann-Whitney U test and M4 is Modified Mann-Whitney U (MMWU) test statistic.
All the ratios for the first and second rows are less than 1.0 which implies the method used as numerator is better and more reliable than the method used as denominator for all the sample sizes considered, i.e. Median Test is better than Modified Median intrinsically Adjusted for Ties (MMED) using Relative Efficiency (Table 11).
Moreover, considering methods 3 and 4 for asymmetric distribution, M4 (Modified Mann-Whitney U test) is better than M3 (Mann-Whitney U test) since the values of R.E are all greater than 1.0. Considering symmetric distribution, the efficiency of M3 (Mann-Whitney U test) is better/stronger for small sample size (5) and as sample size increases, the strength of M4 (Modified Mann-Whitney U test) increases and outweighs M3 (Mann- Whitney U test); this implies that the method is inconsistent because its efficiency decreases as sample size increases.
As shown in Table 12, Median test has lower error rate which makes it better than MMED. This can be interpreted thus, the usual Median test statistic is a better test statistic when testing relevant hypothesis. Error rate of MMED increases as sample size increases which implies MMED is better used for small sample sizes than the large sample size; but Median test statistic is found to be more adequate for both small and large sample sizes and hence should be preferable.
As shown in Table 13, Mann-Whitney U test statistic is more suitable irrespective of the nature of distribution of set of available data as the error rates of MMWU are significantly high. See Table 13. It can be deduced that the sensitivity of the test statistics is independent of sample size of the data but the distribution; either symmetric or asymmetric distribution.
Power of test were computed from Table 12 and Table 13.
Power of test is the sensitivity of a test statistic and the greater the value, the more sensitive the test statistic for both symmetric and asymmetric distributions. Median test is more sensitive than MMED because median has higher power than MMED irrespective of the sample sizes.
Considering both Mann-Whitney and MMWU, Mann-Whitney U test is more sensitivity than MMWU for both symmetric and asymmetric distribution. For better understanding of sensitivity of the four test statistics, line chart of power of test is constructed as shown in Figure 1 and Figure 2; Line chart can be used to show position of the strength or power of a test statistic especially in statistical inference. This shows test statistic with higher power with the maximum power of 1.0. See Figure 1 and Figure 2.
5. Graphical Illustration of Power of Test
As shown in Figure 1, irrespective of sample size; either large or small, the median test statistic has higher power than the modified median test which makes it more appropriate. The modified median test is sensitive to sample size as its power decreases as sample size increases.
As shown in Figure 2, irrespective of sample size; either large or small, the Mann-Whitney U test statistic has higher power than the modified Mann-Whitney U test which makes it more appropriate. The modified method has considerably low power as sample size varies/increases.
![]()
Table 10. Relative efficiency of the test statistics.
![]()
Table 12. Error rate of the median and modified median test statistics.
![]()
Table 13. Error rate of Mann-Whitney and MMWU test statistics.
![]()
Figure 1. Power of median and modified median test for both symmetric and asymmetric distribution.
![]()
Figure 2. Power of Mann-Whitney U and Modified Mann-Whitney U test for both symmetric and asymmetric distribution.
6. Summary and Conclusion
We have in this paper presented a nonparametric statistical method for the analysis of two sample tests. Based on the result of the analysis used, it is observed that for both symmetric and asymmetric distributions, median test is more efficient than Modified Median (MMED) test using relative efficiency as a measure of the efficiency of test statistic since the relative efficiency values are less than 1.0 while in terms of power of test for both symmetric and asymmetric distributions, median test is more sensitive than Modified Median (MMED) test since it has higher power. For Mann-Whitney U test and Modified Mann-Whitney U test (MMWU) using both relative efficiency and power of test, Mann-Whitney U test is more efficient and more sensitive than Modified Mann-Whitney U test (MMWU) since the relative efficiency values are greater than 1 and also it has higher power. In terms of sample size, efficiency of the method is independent of sample sizes except Modified Median Test which has higher power for small sample sizes.