Experimental Investigation of “Scale Influence on Plastic Rotational Capacity of Reinforced Concrete Beams” ()
Received 8 March 2016; accepted 21 April 2016; published 26 April 2016

1. Introduction
The influence of size-scale on the inelastic rotational capacity is an important point to guarantee the structural safety, in fact the experimental data available, mostly obtained by load-controlled tests on reinforced concrete beams with normal and high ductility bars, didn’t show a considerable result. On the other hand, some numerical evaluations, assuming strain localization in the compression zone, indicate that size scale has an influence on the value of the plastic rotation, recent studies and experimental tests seem to validate this dependency [2] . Regarding the failure mode of RC beams in flexure which is affected by nonlinearities of the constituent materials such as concrete tensile cracking, concrete compressive crushing and steel yielding, their interaction depends on the geometrical and mechanical parameters of the beams and can be herein analysed by varying the beam size and the beam slenderness.
Numerical calculation indicates that plastic rotation is subjected to remarkable size effect, according to some studies (Ozbolt and Bruckner, 1999), based on fracture mechanics, it is revealed that the plastic rotation capacity depends on beam size-scale, in contrast with design assumptions, where the plastic rotation is independent of the beam size.
One of the ways to express the ductility of a reinforced concrete beam is the ultimate plastic rotation; as a rule this is defined as the inelastic rotation in correspondence with the ultimate bending moment [3] . Assuming the usual stress-strain relation of steel and concrete, the maximum moment is reached for lower values of curvature. With more realistic assumption, the peak value would be achieved for further curvature. In the following analysis, the ultimate rotation values was computed in correspondence with a relative curvature at a moment equal 90% of the peak value of the descending branch. The rotation obtained in this way has been purified from the elastic value, assumed in correspondence with the yield strength of reinforcement.
Without considering the second order effect and considering the non linear behavior of the material and the tension stiffening, the code (CEB, 1993) indicates that, for the position of the load assumed, the mean value of the material properties remains invariant until the yielding value of the steel has been reached in the critical section. Once this limit is reached, for the material properties, the calculated value must be assumed in correspondence of the critical sections and the maximum capacity is assumed to be equal to the one at the ultimate limit state [4] .
The critical sections are localized in correspondence of the peak value of the bending moment through the zones where these characteristics have the same sign. In absence of the axial force and with a constitutive law of the steel elastic-plastic hardening, it is possible to assume, when the yielding point of steel is reached, that the critical sections acted like a plastic hinges up to the ultimate moment value. While the plastic rotation reaches its ultimate value [5] .
It is likely to assume a third segment of the constitutive law of the section, defined in a reference of translated system with origin in the yielding point of steel, in which its inclination is defined as the ratio between the difference of the ultimate moment values and the permitted plastic rotation as mentioned above.
This paper presents an experimental investigation and aims to evaluate and study eventual relation between scale and plastic rotational capacity and its influence on the ductility of reinforced concrete beams in flexure with detailed experiments. Some useful information and results are given in this paper.
2. Laboratory Test Procedure
The experimental investigation herein considered was executed on three different size-scales of beams with cross-sectional area 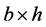 equals to: (A) 100 × 100 mm, (B) 100 × 200 mm and (C) 200 × 400 mm and five different tensile reinforcement ratios, ρ = 0.12%, 0.25%, 0.50%, 1.0% and 2.0%. The beams, characterized by an effective to total depth ratio d/h = 0.9, have been subjected to a three-point bending test. All beams have been realized with the same concrete cast. (For main steel and stirrups arrangement see Figure 1), different slenderness, (
equals to: (A) 100 × 100 mm, (B) 100 × 200 mm and (C) 200 × 400 mm and five different tensile reinforcement ratios, ρ = 0.12%, 0.25%, 0.50%, 1.0% and 2.0%. The beams, characterized by an effective to total depth ratio d/h = 0.9, have been subjected to a three-point bending test. All beams have been realized with the same concrete cast. (For main steel and stirrups arrangement see Figure 1), different slenderness, (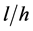 span to depth ratio), of 6, 12 and 18 are used. The testing machine used was a closed-loop servo- controlled machine. The tests were performed in displacement-controlled conditions to be able to record the descending branch of the load-displacement curve, if any. The values of the experimental parameters of the beams are reported in Table 1.
span to depth ratio), of 6, 12 and 18 are used. The testing machine used was a closed-loop servo- controlled machine. The tests were performed in displacement-controlled conditions to be able to record the descending branch of the load-displacement curve, if any. The values of the experimental parameters of the beams are reported in Table 1.
3. Theoretical Model
The plastic rotation is expressed as a function of the ratio  between the neutral axis depth and the effective depth of the beam without ignoring that this ratio is related to the reinforcement ratio, while recent studies have also considered the steel ductility effect (Lounis et al., 2010).
between the neutral axis depth and the effective depth of the beam without ignoring that this ratio is related to the reinforcement ratio, while recent studies have also considered the steel ductility effect (Lounis et al., 2010).
![]()
Table 1. Characteristic loads, deflection and rotation of the tested beams.
From the other hand the plastic behavior of the reinforced concrete structures is very influenced by other factors like: The confinement conditions in the compression zone of the beam section, the bond conditions between steel bars and concrete, bending moment gradient, scale effect, test procedure and the area of the contact zone between the applied load and the beam surface.
The definition of the plastic rotation is always related to the calculation method adapted to the structural analysis. In indeterminate structures, the definition used is that given in (CEB, 1993). The plastic rotation 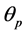 will be obtained by integration along the plastic zone
will be obtained by integration along the plastic zone 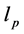 (where the stress in the tension steel is greater than its yielding limit) as the deference between the total curvature
(where the stress in the tension steel is greater than its yielding limit) as the deference between the total curvature  and the curvature obtained at the limit of the yielding point of steel
and the curvature obtained at the limit of the yielding point of steel  so:
so:
 (1)
(1)
In (1) the curvatures are obtained from the rotation between the difference of the average strain of the tension line  and the compression one
and the compression one  which corresponds to the signed value of the transducers located at h/10 from the upper and lower edges of the beam section:
which corresponds to the signed value of the transducers located at h/10 from the upper and lower edges of the beam section:
 (2)
(2)
where h is the depth of the cross section of the beam.
The ultimate rotation 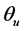 is measured in correspondence of the 90% of the maximum moment in the descending branch, before failure. If this value is not reached so the value in correspondence of failure will be assumed. The ultimate load
is measured in correspondence of the 90% of the maximum moment in the descending branch, before failure. If this value is not reached so the value in correspondence of failure will be assumed. The ultimate load 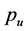 is obtained from the experimental results with the same criteria adopted for the ultimate rotation.
is obtained from the experimental results with the same criteria adopted for the ultimate rotation.
The rotation due to the applied load is given by the effect of superposition as follows:
![]() (3)
(3)
where ![]() and
and ![]() referred to relative depth
referred to relative depth ![]() of the
of the
crack.
Consider ![]() as a local rotation due to the presence of the crack when the applied bending moment reaches its value
as a local rotation due to the presence of the crack when the applied bending moment reaches its value ![]() (the bending moment value at first crack), so the local rotation
(the bending moment value at first crack), so the local rotation![]() , for an initial depth related to the crack
, for an initial depth related to the crack ![]() at the crack propagation, when
at the crack propagation, when![]() , Equation (3) becomes:
, Equation (3) becomes:
![]() (4)
(4)
where ![]()
if ![]() (bending moment which corresponds to the yielding point of steel) and
(bending moment which corresponds to the yielding point of steel) and ![]() if
if![]() .
.
Such linear tendency will stop, when the crack propagation starts.
At this point if the fracture phenomenon is unstable, the relation ![]() presents a discontinuity and its value will correspond to the complete separation of the ligament.
presents a discontinuity and its value will correspond to the complete separation of the ligament.
While if the fracture phenomenon is stable, the discontinuity will vanish and continuous hardening response will be obtained [6] .
4. Experimental Results
The plastic rotation curves versus bending moment are shown in Figures 2-4, where steel ratio and cross section have been maintained constant varying the slenderness ratio as this is the main target of this research, while in Figure 5(a) and Figure 5(b) both slenderness and steel ratio were kept constant varying only beam depth, which will confirm past theories. Beams failure mode, are reported in Figure 6 and Figure 7. Note that for beams Type B and C, the plastic rotation increases with increasing beam size.
Beams type B with slenderness equal to 6 and 12, represented in Figure 2(a) and Figure 2(b) it is easy to observe the different ductility shown by the four beams due to the steel ratio variation, in particular in Figure 2(a) the plastic rotation is higher with respect to the values of the other two beams in Figure 2(a). For beams type A, it's evident that the plastic rotation decreases when increasing the beam size (same cross section 100 × 100 mm).
5. Conclusions
Regarding the scale, in the experimental tests we notice that the plastic rotation has to be related to certain depth of the cross section as a reference to ductility and is still a subject of study as no code takes in consideration the radical effect of beam size in the structural design. For what concern beams type B and C with depth of cross section h ≥150 mm, the plastic rotation increases when increasing beam size as shown in Figure 2 and Figure 3 and the correspondent values reported in Table 1.
While for beams type A with h = 100 mm we find that the plastic rotation decreases when increasing beam size as shown in Figure 4(a) and Figure 4(b), opposite to what we expected and opposite to beams type B and
![]() (a)
(a)![]() (b)
(b)
Figure 2. Plastic rotation vs. bending moment, for beams type B.
![]() (a)
(a)![]()
![]() (a) (b)
(a) (b)
Figure 3. Plastic rotation vs. bending moment, for beams type C.
C due to the difference in the base depth and the amount of reinforcement which have to be considered when we talk about size in reinforced concrete beams, which is still subject of extensive experimental research. So here we
![]() (a)
(a)![]() (b)
(b)
Figure 4. Plastic rotation vs. bending moment, for beams type A.
![]()
Figure 5. Plastic rotation vs. bending moment, for beams type A, B and C.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 6. Failure mode beam type C.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 7. Beam type C with slenderness ratio equal 12.
emphasize that we can’t separate the study of the relation between plastic rotation and size-scale without relating it to a certain beam depth and steel ratio, which needs to be checked and determined.
While for what concern the beam depth, in general, we confirm that the plastic rotation decreases when increasing the beam depth as seen in Figure 5(a), Figure 5(b), Figure 6 and Figures 7(a)-(c). This way of describing this phenomenon is equivalent to what has been indicated by CEB, where the plastic rotation expression is related to the depth of the neutral axis x at ultimate limit state and the total depth of the beam d. The difference in ductility, shown by the curves, is very clear and again confirms that the plastic rotation value decreases when the beam depth increases. The values of the experimental parameters, which describe the above comments, are shown in Table 1.
Acknowledgements
The author of this paper would like to acknowledge for the sincere support of Zarqa University in Jordan.