Received 20 March 2016; accepted 23 April 2016; published 26 April 2016

1. Introduction
In the ever-changing today’s society, talent has increasingly become the key topic. As the cradle of talent training, colleges and universities also attract people’s focus of attention. Colleges and universities shoulder the responsibilities for conveying fresh blood for society and making basic research. The development of colleges is closely related to the development of country. So many charitable organizations dedicate to donations to improve educational performance.
The Goodgrant Foundation is a charitable organization that wants to improve educational performance of undergraduates attending colleges and universities in the US. So the Foundation plans to contribute 50 million money for a suitable team of schools per year under the condition of avoiding repeated other large grant organizations’ investment.
To do this, two questions are solved for the Goodgrant Foundation: how to choose a suitable team of schools and how to allocate the investment. In order to solve the two questions, the DEA model is established to determine an optimal investment strategy, including the selection of schools and determination of investment amount. In this process, DEAP software and MATLAB software are used to solve the questions we face.
2. The DEA Model
2.1. Assumptions
Before solving the questions above, some assumptions are made as follows:
1) Since the period of education investment return is long, only one cycle is considered.
2) Assume that the paper does not consider the school’s ownership such as Public, Private nonprofit and Private for-profit is not considered.
3) Assume that the wages of students after graduation directly reflected in the return on investment.
4) Assume that the school’s all indicators are static.
2.2. The Essential Definitions
Let us consider a set of ,
, 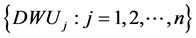 , where
, where  consumes multiple positive inputs
consumes multiple positive inputs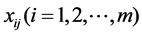 to produce multiple positive outputs
to produce multiple positive outputs . Suppose that inputs and outputs for
. Suppose that inputs and outputs for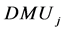 are denoted by
are denoted by  and
and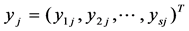 , and
, and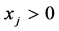 ,
, 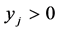 for
for .
.  is the evaluated unit, whose input vector and output vector are respectively recorded as
is the evaluated unit, whose input vector and output vector are respectively recorded as  and
and . Let
. Let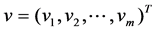 , where
, where ![]() is the weight with regard to the
is the weight with regard to the ![]() th input and
th input and ![]() where
where ![]() is the weight with regard to the
is the weight with regard to the ![]() th output.
th output.
2.3. The CCR Model
DEA (Data Environment Analysis) [12] is a nonparametric technique for measuring the relative efficiencies of a set of decision-making units (![]() ) which consume multiple inputs to produce multiple outputs. Nowadays,
) which consume multiple inputs to produce multiple outputs. Nowadays,
DEA has become increasingly popular for efficiency analysis in practical viewpoint of management, economics, especially the education. So it is meaningful and necessary to apply DEA model in this question.
There exist various DEA models with different economic meanings. The CCR model is chosen in this paper, CCR model which measures the efficiency is the first model of DEA displayed as follows.
![]() (1)
(1)
where
![]() (2)
(2)
Due to the fractional programming model, the model is reformed into a linear programming model to solve as follows.
![]() (3)
(3)
where
![]() (4)
(4)
The fractional programming and linear programming are equivalent [13] .
The dual problem of Equation (3) is as follows.
![]() (5)
(5)
Both Equation (3) and Equation (5) have the optimal solution, and the optimal value ![]() [13] .
[13] .
If the optimal solutions are![]() , some conclusions are obtained as follows:
, some conclusions are obtained as follows:
1) If the optimal value of Equation (5) is ![]() and
and![]() ,
, ![]() is DEA efficiency. It means that the inputs and outputs of each DMU reach the optimal state.
is DEA efficiency. It means that the inputs and outputs of each DMU reach the optimal state.
2) If the optimal value of Equation (5) is![]() ,
, ![]() is weak efficiency.
is weak efficiency.
3) If the optimal value of Equation (5) is![]() ,
, ![]() is under have no efficiency. It regard as the inputs and outputs of each
is under have no efficiency. It regard as the inputs and outputs of each ![]() does not reach the proper ratio.
does not reach the proper ratio.
2.4. The Resource Allocation Model
According to the CCR model, an equivalent change is made on the first equation of the model [14] .
![]() (6)
(6)
For the![]() , right hand side of the equation is denoted as follows:
, right hand side of the equation is denoted as follows:
![]() (7)
(7)
where k represents the kth DMU, ![]() represents the overall size of the kth DMU and it is equal to the product of the scale and efficiency. So we can construct each of DMU in the allocation plan as follows:
represents the overall size of the kth DMU and it is equal to the product of the scale and efficiency. So we can construct each of DMU in the allocation plan as follows:
![]() (8)
(8)
3. DEA Model to the Goodgrant’s Investment Strategy
3.1. Data Preprocessing
Because the formats of the data are various and missing values are different, the data should be preprocessed to avoid inaccuracy and instability caused by redundant data in the data mining. Firstly, the irrelevant or redundant data are deleted to make dimensionality reduced. For example, the name of schools are omitted, the schools’ official website and other characters data are not considered. Secondly, the reasonable data are used to deal with missing values. For example, the plural are used to fill the scalar data such as the index “LACALE “in the data and the mean value of no missing values is used to fill the numerical data.
To be clear, the EXCEL software is used to manipulate the data by the approaches we discussed above. Finally, some appropriate inputs and outputs are chosen. Through the data preprocessing and simple analysis, eight key factors are chosen: 6 inputs and 2 outputs. The DMUs are denoted as schools. After the data preprocessing, the number of schools decreased from 293 to 23. The inputs and outputs considered are as Table 1.
3.2. Establishment of the CCR Model and Resource Allocation Model
The CCR model is as follows:
![]() (9)
(9)
The allocation model is as follows:
![]() (10)
(10)
![]() (11)
(11)
According to our analysis, the variables in the model are![]() , and then use some software to solve the model.
, and then use some software to solve the model.
3.3. Solving the Case
1) School ranking. The software DEAP 2.1 is used to implement CCR case of DEA. Owing to the data, the efficiency scores are got according to the DEA model. Then the schools are ranked according to the efficiency scores. So the schools are sorted by “crste” in the below chart. The degression of scale benefits show investment will not increase efficiency. So schools that are in the condition of scale benefit degression are deleted. Finally, the schools based on the overall efficiency are re-ranked. And the results are listed as Table 2.
2) Allocation of investment. Firstly, ![]() is got from solving the CCR model, where
is got from solving the CCR model, where ![]() is the weight with regard to the ith input. Then the EXCEL is used to obtain the weights of allocation, allocate investment amount for schools we identified. The results are as Table 3.
is the weight with regard to the ith input. Then the EXCEL is used to obtain the weights of allocation, allocate investment amount for schools we identified. The results are as Table 3.
3.4. Results
After a series of analysis, the optimal investment strategy is obtained. The efficiency of schools is measured with the DEA model, and the efficiency scores are used to rank schools. Then, the investment amount is allocated based on the rank and weights of allocation solved by DEA model. So the Goodgrant Foundation can make optimal strategy for future educational investment.
4. Sensitivity Analysis
If the efficiency remains unchanged, but the inputs increase (![]() ), how much should the outputs of the
), how much should the outputs of the ![]() increase (
increase (![]() )? To formulate the question, the inverse DEA model is established to carry on the sensitivity analysis. The inverse DEA model is as follows:
)? To formulate the question, the inverse DEA model is established to carry on the sensitivity analysis. The inverse DEA model is as follows:
Notes: crste is the Overall efficiency; vrste is the True technical efficiency; scale is the Scale efficiency; rts is the Scale Report, irs is increase, - is constant; drs is decrease.
![]()
![]()
Table 3. The school investment table.
![]() (12)
(12)
Then we can select ![]() according to the specific circumstances.
according to the specific circumstances.
5. Conclusions
To deal with the investment strategy problem for the Goodgrant Foundation, the DEA model is used to determine an optimal investment strategy in this paper. And two questions are solved about how to choose a suitable team of schools and how to allocate the investment. The CCR model is used to rank schools which use efficiency from DEAP 2.1 in order to solve the first question. Then, the resource allocation model is established to allocate investment. Finally, the optimal investment strategy is obtained for Goodgrant Foundation.
But in the analysis process, data processing may have tolerance, because the initial data have so many indexes and we have obtained part of indexes of every school. Because only the representative indexes are considered in this paper, some important indexes might be ignored; so some errors might appear in the result of data process- ing. And in model assumptions, the results will have a certain impact without considering some variables such as investment cycle. In the future, these factors in the improved model are investigated.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (71540028, F012408), and Major Research Project of Beijing Wuzi University. Beijing Key Laboratory (NO: BZ0211), Beijing Intelligent Logistics System Collaborative Innovation Center.
Appendix
MATLAB Program
clear;
formatshortg
X = load('c:\x.txt');
Y = load('c:\y.txt');
n = size(X',1); m = size(X,1); s = size(Y,1);
A = [-X' Y'];
b = zeros (n, 1);
LB = zeros(m + s, 1); UB = [];
for i = 1:n;
f = [zeros (1, m) -Y(:,i)'];
Aeq = [X(:,i)' zeros(1,s)]; beq = 1;
w(:,i) = LINPROG(f, A, b, Aeq, beq, LB, UB);
E(i, i) = Y(:,i)'*w(m + 1:m + s,i);
end
Omega = w(1:m,:)
mu = w(m + 1:m + s,:)
NOTES
![]()
*Corresponding author.