A Theoretical Model of pH-Based Potentiometric Biosensor Based on Immobilized Enzyme Membrane ()
Received 4 March 2016; accepted 19 April 2016; published 22 April 2016

1. Introduction
A potentiometric biosensor is a type of chemical sensor that may be used to find the concentration of some components of the analyte. These sensors measure the electrical potential of an electrode when no voltage is present. The potentiometric biosensors have been widely used in environmental, medical and industrial applications [1] . Also potentiometric biosensor can be used for detection of all OPs but they don’t have low enough limits of detection [2] .
The theoretical modeling of biosensors involves solving the system of linear/non-linear reaction-diffusion equations for substrate and product with a term containing a rate of biocatalytical transformation of substrate. The complications of modeling arise due to solving the partially differential equations with non-linear reaction term and with complex initial and boundary conditions. The modeling of biosensor is analyzed by numerical [1] and analytical method [3] of partial differential equation with various boundary conditions. Recently Meena and Rajendran (2010) discussed a theoretical model of a pH-based potentiometric biosensor immobilizing organophosphorus hydrolase (OPH) for steady state conditions [4] .
Rahamathunissa and Rajendran (2008) implemented He’s variational iteration method in nonlinear boundary- value problems in enzyme substrate reaction diffusion processes in amperometric biosensor [5] . Manimozhi et al. [6] presented the solution of steady-state substrate concentration in the action of biosensor response with mixed enzyme kinetics under a Michalis-Menten scheme. Analytical solutions for the steady-state current at a microdisk chemical sensor have been reported by Dong and Che [7] and by Lyons et al. [7] [8] . Recently, Eswari and Rajendran [9] derived the concentration profile of the product of the enzyme reaction and the electrode current for all values of Michalis-Menten constant using the Homotopy perturbation method.
To our knowledge, no general analytical expressions of the concentrations of the substrate, hydrolysis products, added external buffer and hydrogen ions have been reported for all values of parameters. The purpose of this communication is to derive an analytical expression of non-steady state concentrations of OPs and the deprotonation products for all values of reaction parameter using new homotopy perturbation method.
2. Mathematical Formulation of the Problem
The complete description of the problem is given in [4] [10] . For the sake of completeness the brief description is given in this section and Appendix-A. A schematic diagram of the pH-based potentiometric biosensor immobilizing organophosphorus hydrolase (OPH) is represented in Figure 1.
In this figure, S denotes the substrate of organophosphorus pesticides (OPs).  and
and  are represent the hydrolysis products of organophosphodiester and alcohol respectively.
are represent the hydrolysis products of organophosphodiester and alcohol respectively. 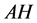 is the added external buffer and
is the added external buffer and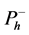 ,
,  ,
, 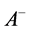 ,
, 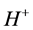 are the deprotonation products. The general scheme that represents an enzyme-cata- lyzed reaction within enzyme membrane can be written as follows:
are the deprotonation products. The general scheme that represents an enzyme-cata- lyzed reaction within enzyme membrane can be written as follows:
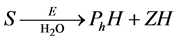 (1)
(1)
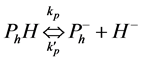 (2)
(2)
![]()
Figure 1. Schematic representation of pH-based potentiometric biosensor immobilizing OPs (organophosphorus pesticides).
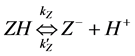 (3)
(3)
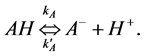 (4)
(4)
The non-linear reaction-diffusion equations for non-steady state condition can be described as follows
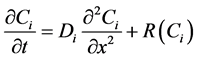 (5)
(5)
where 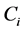 is the concentration of species,
is the concentration of species,  is the diffusion coefficient and
is the diffusion coefficient and ![]() is the reaction rate. The reaction rate is a non-linear function of concentration of substrate. The reaction rate is non-linear with respect to substrate because of product inhibition, saturation of the enzyme with substrate, reverse reaction and enzyme loading. The nomenclature is also presented in Table 1.
is the reaction rate. The reaction rate is a non-linear function of concentration of substrate. The reaction rate is non-linear with respect to substrate because of product inhibition, saturation of the enzyme with substrate, reverse reaction and enzyme loading. The nomenclature is also presented in Table 1.
3. Dimensionless Form
The dimensionless reaction-diffusion equations for non-steady state condition can be written as follows (Appendix A):
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where![]() ,
, ![]() and
and ![]() denotes the sum of dissociated and undissociated concentrations of the species
denotes the sum of dissociated and undissociated concentrations of the species![]() ,
, ![]() , and
, and ![]() respectively and
respectively and ![]() is the concentration of hydrogen ions. Here the Thiele modulus a, which represents the ratio of the characteristic time of the enzymatic reaction to that of the substrate diffusion is
is the concentration of hydrogen ions. Here the Thiele modulus a, which represents the ratio of the characteristic time of the enzymatic reaction to that of the substrate diffusion is
![]() (11)
(11)
The initial and boundary conditions for the above equations becomes
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
A graphical representation of the boundary conditions of this system conditions can be seen in Figure 2.
4. Analytical Expression of Concentration of Substrate and Products Using New Homotopy Perturbation Method (New HPM) and Laplace Transform Technique
With the rapid development of nonlinear science, there appears an ever-increasing interest of scientists and engineers in the approximate analytical asymptotic techniques for nonlinear problems [11] . It is very difficult to solve nonlinear problems either numerically or theoretically. Perturbation methods provide the most versatile tools available in nonlinear analysis of engineering problems, and they are constantly being developed and applied to ever more complex problems. Homotopy perturbation method was first proposed by the He [12] . Recently, a new approach to HPM is presented to solve the nonlinear problem and this gives a simple approximate solution in the zeroth iteration [13] . By using this new homotopy perturbation method and Laplace transform technique (Appendix B), the concentrations of substrate and products can be obtained as follows:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
where
![]() (20)
(20)
5. Results and Discussion
Equations (15) to (19) represents the general new closed-form of analytical expression for the concentrations of substrate![]() , hydrolysis products
, hydrolysis products ![]() and
and![]() , added external buffer concentration of species (AH)
, added external buffer concentration of species (AH) ![]() and hydrogen ions
and hydrogen ions ![]() for non-steady state condition for all values of parameters (Thiele modulus, initial concentration of substrate and products). It is of interest to compare the influence of each parameter on the concentration of species for various values of the parameters.
for non-steady state condition for all values of parameters (Thiele modulus, initial concentration of substrate and products). It is of interest to compare the influence of each parameter on the concentration of species for various values of the parameters.
The kinetic response of a pH-based potentiometric biosensor depends on the concentration of substrate. How- ever, substrate concentration depends on two factors, ![]() and
and![]() . The dimensionless parameter
. The dimensionless parameter ![]() depends upon a and
depends upon a and![]() . “a” is the Thiele modulus, which represents the ratio of the characteristic time of the enzymatic reaction to that of substrate diffusion. When the Thiele modulus “a” is small, the kinetics dominates and the uptakes of the substrate are kinetically controlled. The response is under diffusion control, when the Theile modulus is large (
. “a” is the Thiele modulus, which represents the ratio of the characteristic time of the enzymatic reaction to that of substrate diffusion. When the Thiele modulus “a” is small, the kinetics dominates and the uptakes of the substrate are kinetically controlled. The response is under diffusion control, when the Theile modulus is large (![]() ), which is observed at high catalytic activity and great membrane thickness or at low Michaelis constant or diffusion coefficient values.
), which is observed at high catalytic activity and great membrane thickness or at low Michaelis constant or diffusion coefficient values.
1) Influence of time on the concentration of species. Figures 3(a)-(f) represent concentration of the substrate
versus dimensionless distance for fixed values of a and ![]() and various values of time
and various values of time![]() . From Figures 3(a)-(d), it is inferred that concentration of substrate increases when time
. From Figures 3(a)-(d), it is inferred that concentration of substrate increases when time ![]() increases. The concentration of substrate is in uniform or in steady state when, time
increases. The concentration of substrate is in uniform or in steady state when, time ![]() and Thiele modulus and buffer concentration are small. From Figure 3(e) and Figure 3(f), it is observed that concentration of substrate is in uniform or in steady state when, time
and Thiele modulus and buffer concentration are small. From Figure 3(e) and Figure 3(f), it is observed that concentration of substrate is in uniform or in steady state when, time ![]() and Thiele modulus is large.
and Thiele modulus is large.
2) Influence of Thiele modulus on the concentration of species. The influence of Thiele modulus on the concentration of the substrate for some values of other parameters is shown in Figures 4(a)-(f). The concentration of the substrate strongly depends on Thiele modulus a. From this figure, it is observed that the concentration of substrate decreases when Thiele modulus increases. The concentration of substrate is in uniform or in steady state when Thiele modulus![]() .
.
3) Influence of added buffer concentration on the concentration of species. The influence of added buffer concentration on the concentration of the substrate for some values of other parameters is shown in Figures 5(a)-(e). From this figure, it is inferred that the concentration of the substrate increases when added buffer concentration increases. Solid lines represent the Equation (15) and the dotted lines represent the numerical simulation. Satisfactory agreement is noted. The MATLAB program also given in Appendix B.
Figures 6(a)-(h) show the dimensionless non-steady state concentration profiles of products![]() ,
, ![]() and
and ![]() versus dimensionless distance
versus dimensionless distance ![]() for fixed values of
for fixed values of ![]() and
and ![]() and various values of the parameter a using Equations (16), (17) and (18). From this Figure 6(a) and Figure 6(b), it is observed that the concentration of the product
and various values of the parameter a using Equations (16), (17) and (18). From this Figure 6(a) and Figure 6(b), it is observed that the concentration of the product ![]() increases when Thiele modulus increases. Similarly, Figures 6(c)-(h) show that the concentration of the products
increases when Thiele modulus increases. Similarly, Figures 6(c)-(h) show that the concentration of the products ![]() and
and ![]() increases when Thiele modulus increases.
increases when Thiele modulus increases.
Figure 7(a) & Figure 7(b) show the dimensionless non-steady state concentration of substrate ![]() and products
and products![]() ,
, ![]() and
and ![]() versus dimensionless distance for various values of time
versus dimensionless distance for various values of time![]() , using Equations (15)-(18).
, using Equations (15)-(18).
Table 2 and Table 3 represents the comparison of analytical expression of concentration of the substrate ![]() (Equation (15)) with the numerical result for various values of parameter. In Table 2, average percentage of
(Equation (15)) with the numerical result for various values of parameter. In Table 2, average percentage of
![]()
Table 2. Comparison of analytical expression of concentration of the substrate ![]() (Equation (15)) with the numerical result for various values of parameter a.
(Equation (15)) with the numerical result for various values of parameter a.
![]()
Table 3. Comparison of analytical expression of concentration of the substrate ![]() (Equation (15)) with the numerical result for various values of parameter
(Equation (15)) with the numerical result for various values of parameter![]() .
.
error deviation increases, when the reaction diffusion parameter a increases. Similarly in Table 3, average percentage of error deviation decreases, when the time ![]() increases. In Table 2, the maximum average relative error between the analytical results and numerical results is 0.53%.
increases. In Table 2, the maximum average relative error between the analytical results and numerical results is 0.53%.
6. Conclusion
A non-linear time dependent system of differential equation in pH-based potentiometric biosensor has been solved using the new HPM. New approximate analytical expressions for the concentrations of the substrate and hydrolysis products are derived. The time dependent substrate concentration profiles are also presented using SCILAB program. Concentration of substrate and product depends upon Thiele modulus and initial concentration of substrate which is discussed in this communication.
Acknowledgements
This work was supported by the DST SB/SI/PC-50/2012, New Delhi, India. The authors are thankful to Mr. S. Mohamed Jaleel, The Chairman, Dr. A. Senthilkumar, The Principal, Dr. P. G. Jansi Rani, Head of the Department of Mathematics, Sethu Inistitute of Technology, Kariapatti-626115, Tamilnadu, India for their encouragement.
Appendix A. The Dimensionless Reaction-Diffusion Equations
In the enzyme membrane, the reaction-diffusion equations for the concentration of species for non-steady state condition can be represented as follows [4] [10] .
![]() (A.1)
(A.1)
![]() (A.2)
(A.2)
![]() (A.3)
(A.3)
![]() (A.4)
(A.4)
![]() (A.5)
(A.5)
![]() (A.6)
(A.6)
![]() (A.7)
(A.7)
![]() (A.8)
(A.8)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() are the instantaneous reaction terms. We also assume that the substrate S reacts with the catalysts via Michaelis-Menten kinetics. The reaction rate is
are the instantaneous reaction terms. We also assume that the substrate S reacts with the catalysts via Michaelis-Menten kinetics. The reaction rate is
![]() (A.9)
(A.9)
where
![]() (A.10)
(A.10)
By introducing the following set of dimensionless variables
![]() (A.11)
(A.11)
and defining the following “composite species” [10]
![]() (A.12)
(A.12)
![]() (A.13)
(A.13)
![]() (A.14)
(A.14)
![]() (A.15)
(A.15)
we obtain the dimensionless form of Equations (6)-(10) for the concentration of species which are given in the text.
Appendix B. Analytical Solutions of Equations (6)-(10) Using Complex Inversion Formula
In this appendix, we indicate how the Equations (15) is derived. Using new homotopy perturbation approach [13] , Equation (6) can be written as
![]() (B.1)
(B.1)
![]() (B.2)
(B.2)
The approximate solution of Equation (B.2) is
![]() (B.3)
(B.3)
Substituting Equation (B.3) into Equation (B.2) and arranging the coefficients of powers p
![]() (B.4)
(B.4)
![]() (B.5)
(B.5)
The initial and boundary conditions for Equations (12)-(14) becomes
![]() (B.6)
(B.6)
![]() (B.7)
(B.7)
![]() (B.8)
(B.8)
Equation (B.4) can be written as
![]() (B.9)
(B.9)
where ![]() is defined as in Equation (20). Now, by applying Laplace transform and complex inversion formula (Appendix C) to Equation (B.9) and to the conditions in Equations (B.6)-(B.8), we obtained the solution of Equation (B.9) as
is defined as in Equation (20). Now, by applying Laplace transform and complex inversion formula (Appendix C) to Equation (B.9) and to the conditions in Equations (B.6)-(B.8), we obtained the solution of Equation (B.9) as
![]() (B.10)
(B.10)
Using residue theorem (Appendix C) we can obtain the Equation (15) in the text.
Appendix C. Inverse of Equation (B. 10) by Using Complex Inversion Formula
In this appendix, we indicate how Equation (B.10) may be inverted using the complex inversion formula. If ![]() represents the Laplace transform of a function
represents the Laplace transform of a function![]() , then, according to the complex inversion formula, we can state that
, then, according to the complex inversion formula, we can state that
![]() (C.1)
(C.1)
where the integration in Equation (C.1) is to be performed along a line ![]() in the complex plane where
in the complex plane where![]() . The real number c is chosen such that
. The real number c is chosen such that ![]() lies to the right of all the singularities but is otherwise assumed to be arbitrary. In practice, the integral is evaluated by considering the contour integral presented on the right-hand side of Equation (C.1), which is then evaluated using the so-called Bromwich contour. The contour integral is then evaluated using the residue theorem which states, for any analytic function
lies to the right of all the singularities but is otherwise assumed to be arbitrary. In practice, the integral is evaluated by considering the contour integral presented on the right-hand side of Equation (C.1), which is then evaluated using the so-called Bromwich contour. The contour integral is then evaluated using the residue theorem which states, for any analytic function![]() , that
, that
![]() (C.2)
(C.2)
where the residues are computed at the poles of the function![]() . Hence, from Equation (C.2), we note that
. Hence, from Equation (C.2), we note that
![]() (C.3)
(C.3)
From the theory of complex variables, we can show that the residue of a function ![]() at a simple pole at
at a simple pole at ![]() is given by
is given by
![]() (C.4)
(C.4)
Hence, in order to invert Equation (B.10), we need to evaluate
![]() (C.5)
(C.5)
The poles are obtained from![]() . Hence, there is a simple pole at
. Hence, there is a simple pole at ![]() and there are infinitely many poles given by the solution of the equation
and there are infinitely many poles given by the solution of the equation ![]() and so
and so
![]() (C.6)
(C.6)
Hence, we note that
![]() (C.7)
(C.7)
The first residue in Equation (B.17) is given by
![]() (C.8)
(C.8)
The second residue in Equation (B.17) is given by
![]() (C.9)
(C.9)
where ![]() is defined as in Equation (20). Here, we used
is defined as in Equation (20). Here, we used ![]() and
and![]() . From Equations (C.7)-(C.9), we conclude that
. From Equations (C.7)-(C.9), we conclude that
![]() (C.10)
(C.10)
where ![]() is defined as in Equation(20). Similarly, we can solve Equations (7) to (10) by using complex inversion formula.
is defined as in Equation(20). Similarly, we can solve Equations (7) to (10) by using complex inversion formula.
Appendix D. Scilab/Matlab Program to Find the Numerical Solutions of Equations (15) to (18)
function pdex4
m = 0;
x = linspace(0,1);
t = linspace(0,10);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
figure
plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,2)')
%――――――――――――――――――――――
%figure
%plot(x,u2(end,:))
%title('u2(x,t)')
%xlabel('Distance x')
%ylabel('u2(x,2)')
%――――――――――――――――――――――
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1];
f = [1; 1].*DuDx;
a=5;
F1 = -(a^2*u(1))/(1+u(1));
F2 = -(a^2*u(1))/(1+u(1));
s = [F1;F2];
% ――――――――――――――――――――?
function u0 = pdex4ic(x)
u0 = [0; 0];
% ――――――――――――――――――――?
function [pl,ql,pr,qr] = pdex4bc (xl,ul,xr,ur,t)
pl = [0;0];
ql = [1;1];
pr = [ur(1)-1;ur(2)-0];
qr = [0; 0];
NOTES
![]()
*Corresponding author.