A Comparison of Malware Detection Techniques Based on Hidden Markov Model ()
Received 25 January 2016; accepted 19 April 2016; published 22 April 2016

1. Introduction
Malware is a software which is developed for malicious intent [1] . Malware can steal sensitive data from a computer or it can infect files one after the other, and spreads the infection throughout the computer. Malware needs to be caught and removed from the infected computer promptly to avoid the leakage of sensitive data or any other malicious activity in the computer. Malwares can be classified into viruses, worms, Trojans, spywares, adwares, Rootkits, etc. [2] .
To escape detection tools, malware developers evolve new techniques [3] [4] . They write malware in a fashion that it changes its appearance and alters its code on each infection―thus changes its appearance on each infection. Therefore, the signature-based detection schemes cannot detect them. The various techniques employed by malware developers are discussed below.
2. Obfuscation Techniques
Obfuscation techniques that change the syntax of program without change the semantic that make the malicious code more difficult to be analyzed and understand while preserving its semantics and functionality [5] . Obfuscation can be achieved by register exchange where registers and variables within the file are switched but the code remains the same; instruction swap, which substitutes instructions with equivalent instructions; instruction permutation; transposition that reorders the independent instructions; dead code insertion where “do nothing” instructions are inserted in the code [6] .
2.1. Code Encryption
Refers to hiding the malicious code. Encrypted malware comprises of decryption/encryption engine, decryption key and encrypted malicious code [2] . Encrypted malwares can be classified.
2.2. Oligomorphic
The malware developers encrypt the code in a manner that it can change its decryptors lightly [2] . However, this malware has some limitations and can be detected by signature-based detection tools [7] .
2.3. Polymorphic
The polymorphic malware encrypts itself with a different encryption algorithm/key in every infection. It can use a large number of encryption algorithms/keys and thus makes its detection very difficult and time consuming [3] .
2.4. Metamorphic
The metamorphic malware is capable of changing itself to a completely new instance that does not have anything common to its original [2] . This behavior makes it the most complicated malware to detect.
3. Malware Detection Techniques
Malwares are worldwide epidemic and malware detection techniques (MDTs) serve as first line of defense against them. The effectiveness of a malware detection tool is based on the techniques it uses. Malware detection techniques can be primarily divided into the following three classes.
3.1. Signature-Based Techniques
Signature-based detection is widely used to detect known malware. Although it is very effective, but becomes ineffective if there is even a very small change in the code, which in turn changes its signature. Furthermore, this scheme requires the signature database to be updated on regular basis to detect new malware [6] .
3.2. Behavior-Based Techniques
These techniques constantly observe program behavior to determine whether it is harmful or not. Thus, these techniques can also detect unknown malware. However, the effectiveness of these techniques is not yet proven. The experiments show that these techniques have high false positive ratio [3] . Moreover, these techniques take more time in detection process.
3.3. Heuristic Techniques
These techniques mainly use machine learning and data mining methods to identify the behavior of the running program. The major methods that have been used so far include Naive Bayesian, Neural Network and Hidden Markov Model [1] [3] [4] [8] .
In recent work [1] [3] [4] [9] , Hidden Markov Model (HMM) has been shown as an efficient machine learning model to detect malware. HMM is based on statistical analysis of different states of a code, where each state has an associated probability of transition to other states.
HMM is a process modeling technique where each state of the process is defined in terms of its input data and its corresponding probability of occurrence. HMM is initially trained for different states of a malicious code along with its statistical properties. Based on this learning, HMM can detect, with high probability, the malicious codes of the same family. Thus, the more the training of HMM with different variants, the higher the chances of detection.
The following section gives us more details how HMM work.
4. Hidden Markov Model
4.1. Hidden Markov Model Overview
Hidden Markov models (HMMs) are generally used for statistical pattern analysis. Also can be used in speech recognition [10] , malicious code detection [11] and biological sequence analysis [12] .
Hidden Markov model is a statistical model that has states and known probabilities of the state transitions is called a Markov model [13] . In such a Markov model, the states are visible to the observer. But a hidden Markov model (HMM) has states that are not directly observable [10] . HMM is a machine learning technique. HMM acts as a state machine. Every state is associated with a probability distribution for observing a set of observation symbols. The transition between the states has fixed probabilities. We train an HMM using the observation sequences to represent a set of data [13] . We can match an observation sequence against a trained HMM to determine the probability of seeing such a sequence. If the probability is high, the observation sequence is similar to the training sequences. HMMs are used in protein modeling, also can be used for software piracy detection [14] . As mentioned in [13] , the notations used in the hidden Markov models as following (Figure 1):
T = length of the observation sequence
N = number of states in the model
M = number of distinct observation symbols
Q = distinct states of the Markov Model
V = set of possible observations
A = state transition probability matrix
B = observation probability matrix
π = initial state distribution
O = observation sequence
A hidden Markov model is defined by the matrices A, B and π. An HMM is denoted as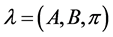 .
.
The following three problems can be solved efficiently using HMM algorithms:
Problem 1: Given a model  and an observation sequence O, we need to find P(O|λ). That is, an observation sequence that can be scored to see how well it fits a given model.
and an observation sequence O, we need to find P(O|λ). That is, an observation sequence that can be scored to see how well it fits a given model.
Problem 2: Given a model 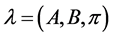 and an observation sequence O, we can determine an optimal state sequence for the Markov model. That is, the most likely hidden state sequence can be uncovered.
and an observation sequence O, we can determine an optimal state sequence for the Markov model. That is, the most likely hidden state sequence can be uncovered.
Problem 3: Given O, N, M, we can find a model λ that maximizes probability of O. This is the training of a model in order to best fit an observation sequence.
These three problems can be efficiently solved by the following three algorithms:
・ The Forward algorithm
・ The Backward algorithm
・ The Baum-Welch re-estimation algorithm
The forward-backward algorithm is for calculating the probability of being in a state qi at time t given an observation sequence O [13] . The forward algorithm, or α pass, determines . The algorithm can be stated as follows.
. The algorithm can be stated as follows.
![]()
Figure 1. Represents a generic view of a hidden Markov model [13] .
1) For 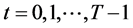 and
and 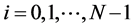
2) 
The probability of the partial observation sequence up to time t is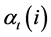 . Using the forward algorithm,
. Using the forward algorithm,  can be computed as follows:
can be computed as follows:
1) Let , for
, for 
2) For  and
and  compute
compute

3) Then ![]()
The backward algorithm helps to find a most likely optimal state sequence. This algorithm can be stated as follows:
1) For ![]() and
and ![]() define
define
2) ![]()
Then ![]() can be calculated in following steps:
can be calculated in following steps:
3) Let![]() , for
, for ![]()
4) For ![]() and
and![]() , compute
, compute
![]()
For ![]() and
and ![]() define
define
![]()
The relevant probability up to time t is given by:
![]()
The most likely state at any time t is the state for which ![]() is maximum. The Baum-Welch algorithm helps in iteratively re-estimating the parameters A, B, π [13] .
is maximum. The Baum-Welch algorithm helps in iteratively re-estimating the parameters A, B, π [13] .
It provides efficient way to best fit the observations. The number of states N and number of unique observation symbols M are constant. However, other parameters like A, B and π are changeable with row stochastic condition. This process of re-estimating the model is explained as follows:
1) Initialize ![]() with an appropriate guess or random values. For example
with an appropriate guess or random values. For example
π = 1/N, Aij = 1/N, Bij = 1/M.
2) Compute![]() ,
, ![]() ,
, ![]() and
and ![]() where
where ![]() is a digamma. The digammas can be defined as:
is a digamma. The digammas can be defined as:
![]()
![]() and
and ![]() are related by:
are related by:
![]()
3) Re-estimate model parameters as: For ![]() let
let
![]()
For ![]() and
and![]() , compute:
, compute:
![]()
For ![]() and
and![]() , compute:
, compute:
![]()
4) If ![]() increases go to Step 3.
increases go to Step 3.
Considering the potential and effectiveness of HMM-based MDTs, we have studied their strengths and weaknesses. In this paper, we examined 10 HMM-based MDTs and compared them to facilitate their selection for designing and developing secure systems. In addition, we also present a comprehensive literature review of MDT.
4.2. HMM as Malware Detection Tool
4.2.1. Traditional HMM Detector
Wong and Stamp in [3] [4] proposed a detection tool based on HMM to detect metamorphic virus. In their work, the authors compared their tool with commercial anti-virus tools for the morphed viruses generated by four virus engines: Next Generation Virus Creation Kit (NGVCK), Second Generation virus generator (G2), Virus Creation Lab for Win32 (VCL32), and Mass Code Generator (MCGEN). The commercial anti-virus could not detect morphed virus generated by NGVCK, whereas HMM based detector not only classified each virus to a particular family but showed a detection rate of 97% with only 3% false positive detections [3] [4] . Figure 2 show the HMM score used to classify the family virus, non-family virus and normal file.
The authors in [6] developed a code obfuscation engine that creates metamorphic viruses, which cannot be detected by any signature based technique, and validate detection based on HMM. The authors created 120 different variants of seed viruses. The code morphing engine randomly shuffles the virus assembly code by dividing it into different blocks and also inserts some blocks of dead code in the original code. These metamorphic viruses were scanned using commercial anti-virus (McAfee), which failed to detect any of these viruses. Then, these metamorphic viruses were tested using the proposed HMM detector. For all of the viruses, the score significantly varied from that for normal files. Thus, the HMM-based detector identified viruses from their similarity score only [6] .
Another work in [15] developed metamorphic engine to produce highly diverse morphed copies of base viruses. The code obfuscation techniques used to develop engine are dead code insertion, equivalent instruction substitute and transposition. These metamorphic viruses were tested against a commercial anti-virus and HMM detector. The results showed that HMM detector is effective to identify metamorphic viruses with high accuracy [15] .
Authors in [8] proposed a code emulator designed to detect dead code in metamorphic virus. This emulator enhanced the effectiveness of HMM detector. The following graph shows us the architecture of the Code Emulator Process Flow. This emulator has capability to emulate all important CPU registers and can filter out changes in the instructions/subroutines caused by code obfuscation. The proposed emulator effectively identified 15%, 25% and 35% morphed viruses [8] .
Shabana et al. [14] used HMM to detect software piracy (Figure 3). In their work, the authors [14] used a metamorphic generator to create morphed copies of a basic code. The authors extracted opcode sequences from these copies and trained HMM on these sequences. Based on this learning, HMM computed similarity score of
![]()
Figure 3. Code emulator process flow [8] .
the suspicious program to the basiccode. The higher the similarity score, the more likely it is that the suspicious program is an altered version of the basiccode, and vice versa. This approach proved to be highly effective for detecting morphed viruses.
4.2.2. Dueling HMM Detector
As mentioned in [3] [4] , HMM detector is effective for detecting metamorphic viruses. The work in [16] explored HMM in more depth. The authors built models for different compilers, extracted salient features of those models and used them in their proposed model to detect metamorphic viruses. In its classical implementation, HMM has been used to mark a file as infected if its virus code similarity exceeds a given threshold [4] [5] . However, authors’ proposed approach marks the suspect file as a virus only if the HMM estimates a high probability by comparing the suspect file with several developed HMMs. This approach proved to be highly effective in detecting the malware that even used advanced metamorphic techniques. On the other hand, this approach is deficient in balancing false negative and false positive results. In addition, this approach suffers from high performance overheads as compared with the work in [4] and [5] . To overcome this problem of high overheads, the work in [13] brings forth a hybrid approach of dueling HMM and traditional HMM.
Thunga and Neelisetti [17] proposed an intelligent classification approach based on HMM to identify viruses of metamorphic family. In the proposed approach, the authors train multiple HMMs, one for each virus family. They represent “n” opcodes sequences in an executable file as “n-gram”. The selection of n-gram affects the overall accuracy of the proposed approach. The n-gram sequence in the metamorphic virus is analyzed by comparing with the trained HMMs one by one using a “log-likelihood similarity measure”. A virus is considered to be a part of the family for which the “log-likelihood similarity measure” is the highest. The authors observed 90% accuracy for each family of viruses. The proposed method is easily scalable for a higher number of virus families. In addition, parallel implementation of the comparison phase makes the method very efficient [17] (Figure 4).
4.2.3. Hyper HMM Detector
Researchers are still working to enhance the HMM detector. The authors in [18] proposed to use genetic algorithm with HMM. In HMM based techniques Baum-Welch method is used for solving one of the three problems [15] , i.e. estimating the parameters of the corresponding HMM given an output sequence. In this work the authors used genetic algorithm to solve the problem. The Baum-Welch algorithm is linear in nature and suffers from the local optima problem. The selection of genetic algorithm over traditional Baum-Welch method lies in the non-linearity of genetic algorithm.
There are two reasons to choose genetic algorithm over Baum-Welch algorithm [18] :
・ Genetic algorithm is a part of random and evolutionary algorithms and does not suffer from the local optima problem but Baum-Welch algorithm suffers from this problem.
![]()
Figure 4. Work flow of the proposed HMM based classifier [17] .
・ Genetic algorithm works on set of populations (comprising of numbers of chromosomes at time, while the Baum-Welch algorithm works on individuals, so the time required to train the model increases and set of opcodes remains shallow.
This proposed work [18] enhances HMM and results in higher accuracy in detecting metamorphic viruses.
Annachatre et al. [1] proposed new approach using HMM to detect metamorphic viruses based on classifier algorithm. In previous works like [3] [4] and [16] , the authors used HMM alone to detect metamorphic viruses. In contrast to these studies, Annachatre et al. used a classifier algorithm to enhance the effectiveness of HMM detector. The authors trained HMMs on a collection of malware. Then these models were evaluated and based on the resulting score the malware samples were separated into clusters using k-means clustering algorithm as a classifier. This work showed the highest accuracy as compared to previous works such as [3] [4] and [16] .
Payandeh et al. proposed a HMM based detection circle in [18] , where he characterized a virus family using three parameters: 1) the amount of virus similarities; 2) specifically-located character occurrence probability; 3) string occurrence probability. The proposed virus detection circle is developed on x, y coordinate axis, where x and y represent probabilities of the factors considered in the study. To evaluate the proposed approach, the authors used NGVCK kit to create morphed malware. Next, they calculated similarity scores of these viruses using Mishra’s algorithm after making using Mishra method samples in each family are compared two by tow. The least, the most and the average quantity of samples comparison in each virus creation kit can be seen in the following Table 1. The proposed approach detected these malware with 91% accuracy. This work shows good result in malware detection but need to improve the detection speed.
![]()
Table 1. Min, Max and average kits similarities percentage.
5. Comparison
6. Research Directions
・ To detect malware based on clustering algorithms such as K-means, decision Tree etc. based on learning models such as HMM and Neural Network.
・ To study how different detection approaches performs against each obfuscation techniques like dead code technique.
7. Conclusion
Malware is any code that is developed for malicious intent. The malware has rapidly become a major security threat for computing community and is the basic reason for the most of the security problems on internet. Recent malware can easily deceive the signature-based detection approaches by altering their code while keeping its function intact. To solve this problem, some machine learning techniques such as, HMM and Neural Network are used. In current study, we have compared several HMM based malware detection approaches. From this survey, we conclude that HMM is an efficient model to detect malware and further studies may focus on how to improve the classification of malware based on HMM as malware detection tool.