Inference in the Presence of Likelihood Monotonicity for Polytomous and Logistic Regression ()
Received 21 November 2015; accepted 19 April 2016; published 22 April 2016

1. Introduction
We consider the problem of inference for a multinomial regression model. The sampling distribution of responses for this model, and, in turn, its likelihood, may be represented exactly by a certain conditional binary regression model.
Some binary regression models and response variable patterns give rise to likelihood functions that do not have a finite maximizer; instead, there exist one or more contrasts of the parameters such that as this contrast is increased to infinity, the likelihood continues to increase. For these models and response patterns, maximum likelihood estimators for regression parameters do not exist in the conventional sense, and so monotonicity in the likelihood complicates estimation and testing of binary regression parameters. Because of the association between binary regression and multinomial regression, multinomial regression methods inherit this difficulty. In particular, methods like those suggested by [1] , using higher-order asymptotic probability approximations like those of [2] , are unavailable in these cases, since the methods of [2] use values of the maximized likelihood, both with the parameter of interested fixed and allowed to vary, and use the second derivatives of the likelihood at these two points.
[3] provides a method for diagnosing and adjusting for likelihood monotonicity for conditional testing in binary regression models. This manuscript extends this method to facilitate estimation in multinomial regression, for approximate inference, and in particular makes practical the use of the approximation of [2] .
Section 2.1 reviews binary and multinomial regression models, and relations between these models that let one swap back and forth between them. Section 2.2 reviews conditional inference for canonical exponential families. Section 2.3 reviews techniques of [3] for performing conditional inference in the presence of likelihood monotonicity for binary regression, makes a suggestion for improving the efficiency of this earlier technique, and expands on its implication for estimation. Section 2.4 reviews some existing techniques for addressing likelihood monotonicity. Section 2.5 develops new techniques for detection of likelihood monotonicity in multinomial regression models, and explores discusses non-uniqueness of maximum likelihood estimates in this case. Section 3 applies the techniques of Section 2.5 to some examples. Section 4 presents some conclusions.
2. Methods and Materials
This section describes existing methods used in cases of likelihood monotonicity in multinomial models, and presents new methods for addressing these challenges.
2.1. Multinomial and Logistic Regression Models
Methods will be developed in this manuscript to address both multinomial and binary regression models. In this section, relationships between these models are made explicit.
Consider first the multinomial distribution. Suppose that M multinomial trials are observed; for trial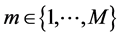 , one of
, one of 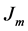 alternatives is observed, with alternative
alternatives is observed, with alternative  having probability
having probability
 (1)
(1)
Here 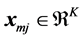 (for
(for 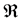 representing the real numbers and K a positive integer) are covariate vectors associated with each of the alternatives, and
representing the real numbers and K a positive integer) are covariate vectors associated with each of the alternatives, and 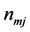 are the number of replicates with this covariate pattern. These probabilities depend only on on the differences between
are the number of replicates with this covariate pattern. These probabilities depend only on on the differences between  and
and 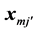 for
for ; without loss of generality we will take
; without loss of generality we will take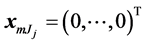 , treating the last category as a baseline. Let
, treating the last category as a baseline. Let 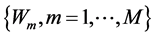 be independent random variables such that
be independent random variables such that 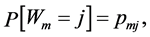 and let
and let 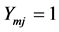 if
if 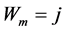 and
and ![]() if
if![]() . Then the variables
. Then the variables ![]() are the indices of the selected multinomial outcomes, and
are the indices of the selected multinomial outcomes, and ![]() are related indicator variables. The likelihood is given by
are related indicator variables. The likelihood is given by
![]() (2)
(2)
Let ![]() be the matrix with
be the matrix with ![]() rows and K columns, with row j given by
rows and K columns, with row j given by![]() , let
, let![]() , and let
, and let ![]() and
and![]() . Then sufficient statistics for
. Then sufficient statistics for ![]() are
are
![]() (3)
(3)
The binary regression model is similar; let ![]() be independent binomial random variables with mass function
be independent binomial random variables with mass function
![]() (4)
(4)
for
![]() (5)
(5)
where![]() , and
, and ![]() a positive integer. Sufficient statistics for
a positive integer. Sufficient statistics for ![]() are given by
are given by
![]() (6)
(6)
for ![]() the
the ![]() matrix with row m equal to
matrix with row m equal to![]() .
.
The binary regression model can be recast as a multinomial regression model. Furthermore, the multinomial regression model may be expressed as a conditional binary regression model. Suppose that (1) and (2) hold. Let ![]() be a matrix with
be a matrix with ![]() rows and M columns, such that the entries in column m are all 1, and all other entries
rows and M columns, such that the entries in column m are all 1, and all other entries
are 0. Let ![]()
![]() (7)
(7)
with ![]() defined analogously, and let
defined analogously, and let ![]() and
and![]() .
.
2.2. Conditional Inference
The model for ![]() given by (4)-(5) represents a canonical exponential family, and so inference on some components of
given by (4)-(5) represents a canonical exponential family, and so inference on some components of ![]() (without loss of generality,
(without loss of generality,![]() ) may be performed by considering the sampling distribution of
) may be performed by considering the sampling distribution of ![]() conditional on
conditional on![]() . Let
. Let ![]() represent the probability mass function for this conditional distribution. The probability mass function for
represent the probability mass function for this conditional distribution. The probability mass function for ![]() of (3), evaluated at
of (3), evaluated at![]() , is exactly the same as
, is exactly the same as
![]()
for![]() . Note here the conditioning event for the larger model is expressed in terms of sample sizes in the smaller model. Furthermore, one can relate probabilities calculated with the regression parameters set to zero, to the probabilities for a general parameter vector
. Note here the conditioning event for the larger model is expressed in terms of sample sizes in the smaller model. Furthermore, one can relate probabilities calculated with the regression parameters set to zero, to the probabilities for a general parameter vector![]() , by
, by
![]() (8)
(8)
When![]() , define the confidence interval for one of the regression parameters (without loss of generality
, define the confidence interval for one of the regression parameters (without loss of generality![]() ) with nominal coverage
) with nominal coverage ![]() for
for![]() , by
, by
![]() (9)
(9)
Then ![]() has coverage probability at least
has coverage probability at least![]() , and can be used as a
, and can be used as a ![]() confidence interval. In fact, the coverage
confidence interval. In fact, the coverage ![]() may be strictly greater than
may be strictly greater than![]() , and more precise intervals with at
, and more precise intervals with at
least ![]() coverage may be constructed as
coverage may be constructed as![]() , for
, for
![]() (10)
(10)
The cumulative probabilities implicit in (9) may be approximated as
![]() (11)
(11)
for ![]() and
and ![]() the standard normal distribution function respectively,
the standard normal distribution function respectively, ![]() , for
, for ![]() the
the
logarithm of the likelihood (in the multinomial regression case, given by (2)), ![]() maximizing
maximizing![]() , with data adjusted for continuity so that
, with data adjusted for continuity so that ![]() is reduced by half,
is reduced by half, ![]() maximizing
maximizing![]() , with
, with ![]() fixed at its null value,
fixed at its null value,
and![]() , with
, with ![]() the matrix of second derivatives of
the matrix of second derivatives of ![]() with respect to all but the first component of the argument [2] .
with respect to all but the first component of the argument [2] .
Similar techniques may be applied to the multinomial regression model, with ![]() of (3) replacing
of (3) replacing ![]() of (6). Denote the conditional sample space by
of (6). Denote the conditional sample space by
![]() (12)
(12)
2.3. Infinite Estimates
This section reviews and clarifies techniques for inference in the presence of monotonicity in the logistic regression likelihood (4) given by [3] , who built on results of [4] - [6] , and [7] . Choose![]() . Let
. Let
![]()
for ![]() the logistic regression likelihood of (4) [3] , building on the results of [4] , determines which observations correspond to extreme fitted probabilities by maximizing the total number of positive entries in both
the logistic regression likelihood of (4) [3] , building on the results of [4] , determines which observations correspond to extreme fitted probabilities by maximizing the total number of positive entries in both ![]() and
and ![]() subject to constraints outlined in the next theorem.
subject to constraints outlined in the next theorem.
Theorem 1. Suppose that random vectors ![]() arise from the model (4) and (5), and matrix
arise from the model (4) and (5), and matrix ![]() is of full rank. Then
is of full rank. Then ![]() is exactly the set of vectors
is exactly the set of vectors
![]() (13)
(13)
with ![]() and
and ![]() column vectors such that
column vectors such that ![]() and such that
and such that
![]() (14)
(14)
![]() (15)
(15)
where ![]() are the sufficient statistics associated with
are the sufficient statistics associated with![]() ,
, ![]() is the observed value of this vector
is the observed value of this vector![]() , and
, and ![]() is a matrix with M rows and rank
is a matrix with M rows and rank![]() , such that
, such that![]() .
.
Furthermore, the conditional probabilities are the same as those arising if observations with positive entries in ![]() or
or ![]() are omitted, and collinear covariates among columns
are omitted, and collinear covariates among columns ![]() removed.
removed.
The matrix ![]() may be constructed from the QR decomposition of
may be constructed from the QR decomposition of![]() . Inference on components of
. Inference on components of ![]() for (4) may be performed conditionally, even when maximum likelihood estimates fail to exist, and hence (11) cannot be used [3] .
for (4) may be performed conditionally, even when maximum likelihood estimates fail to exist, and hence (11) cannot be used [3] .
2.4. Other Approaches
Suppose that there exists a vector ![]() such that
such that
![]() (16)
(16)
with strict inequality holding in place of at least one of the inequalities. Then the likelihood![]() , defined in (2), is a strictly increasing function of a for any
, defined in (2), is a strictly increasing function of a for any![]() , and so no finite maximizer of L exists. This lack of a finite maximizer leads to difficulties with maximum likelihood estimation and inference. This section reviews some existing approaches.
, and so no finite maximizer of L exists. This lack of a finite maximizer leads to difficulties with maximum likelihood estimation and inference. This section reviews some existing approaches.
Bias-correction is possible for maximum likelihood estimators [8] , and may be employed in this type of cituation [9] . Estimates with this correction applied are the same as those maximizing the posterior density of the parameters under the invariant prior of [10] , in which the likelihood function is multiplied by the square root of the determinant of the information matrix; this is equivalent to maximizing a penalized likelihood. That is, if![]() , for
, for ![]() as in (2), then the approach of [8] suggests maximizing
as in (2), then the approach of [8] suggests maximizing ![]() These estimates are always finite. A similar approach is possible in the case of proportional hazards regression, which also gives advantages for testing [11] .
These estimates are always finite. A similar approach is possible in the case of proportional hazards regression, which also gives advantages for testing [11] .
Standard errors may be calculated from the second derivative of the unpenalized log likelihood [8] ; one could also calculate standard errors from the second derivative of the penalized log likelihood [11] . This second approach is used in this manuscript for comparison purposes, and so the asymptotic confidence intervals considered below for ![]() is
is
![]() (17)
(17)
Here the superscript 11 on ![]() represents component 11 of the inverse second derivative matrix of
represents component 11 of the inverse second derivative matrix of ![]() with respect to
with respect to![]() .
.
The approach using Jeffreys’ prior to penalize the likelihood has some disadvantages. The union of all possible confidence intervals resulting as the penalized estimator plus or minus a multiple of the standard error has a finite range, and so the confidence region procedure as described above has vanishing coverage probability for large values of the regression parameter.
2.5. Estimation
We investigate the behavior of maximum likelihood estimates in the multinomial regression model (2). Maximizers for both the original likelihood and for the likelihood of the distribution of sufficient statistics of interest (6) or (3) conditional on the remaining canonical sufficient statistics are considered. Conditional probabilities arising from the logistic regression model (4) are of form (2), and so may also be handled as below.
Consider the occurrence of infinite estimates for model (2). Denote the sample space for the ![]() of (3) by
of (3) by![]() . For a canonical exponential family with finite support, the maximizer of the likelihood associated with a data point
. For a canonical exponential family with finite support, the maximizer of the likelihood associated with a data point ![]() exists if and only if
exists if and only if![]() , where
, where ![]() represents the convex hull of its argument, and the superscript
represents the convex hull of its argument, and the superscript ![]() represents the interior of the set it modifies ( [12] , Theorem 9.4). The following two corollaries may be used to determine if the finite maximizers of (2) exist, in terms of the observed sufficient statistic
represents the interior of the set it modifies ( [12] , Theorem 9.4). The following two corollaries may be used to determine if the finite maximizers of (2) exist, in terms of the observed sufficient statistic ![]() of (3). The first is a corollary to ( [12] , Theorem 9.4).
of (3). The first is a corollary to ( [12] , Theorem 9.4).
Corollary 1. Unique finite maximizers of the likelihood given in (2) exist if and only if ![]() is of rank at least K, and the maximizer of
is of rank at least K, and the maximizer of ![]() subject to
subject to
![]() (18)
(18)
![]() (19)
(19)
is greater than zero.
Proof. If ![]() is not of full rank, then multiple parameter values give the same value of
is not of full rank, then multiple parameter values give the same value of![]() , and maximizers cannot be unique.
, and maximizers cannot be unique.
Suppose that ![]() is of full rank. The set
is of full rank. The set ![]() is defined from (3) as the set of multiples of rows of
is defined from (3) as the set of multiples of rows of![]() , with the multipliers taken from
, with the multipliers taken from![]() , with the sum of indicators associated with a fixed m equal to 1. Let
, with the sum of indicators associated with a fixed m equal to 1. Let
![]() , and let
, and let![]() . The convex hull of
. The convex hull of ![]() is
is
given by![]() . By the theorem of [12] , a finite estimator at the data point
. By the theorem of [12] , a finite estimator at the data point ![]() exists if and only if
exists if and only if![]() . In this case, the interior is defined in terms of the topology of the subset of
. In this case, the interior is defined in terms of the topology of the subset of ![]() containing
containing ![]() subject to (18). The proof is complete when one shows that
subject to (18). The proof is complete when one shows that![]() . Suppose that
. Suppose that![]() . Let
. Let ![]() achieve the maximum as described in the statement of the corrolary. Choose m and j such that
achieve the maximum as described in the statement of the corrolary. Choose m and j such that ![]() is as small as any component of
is as small as any component of![]() . There exists
. There exists![]() ,
, ![]() , such that
, such that![]() . Let
. Let ![]() be the vector configured like
be the vector configured like![]() , consisting of all zeros except for 1 in the
, consisting of all zeros except for 1 in the ![]() place and -1 in the
place and -1 in the ![]() place. There exists
place. There exists ![]() such that
such that![]() . Hence
. Hence ![]() may be chosen so that all components of
may be chosen so that all components of ![]() are non-negative, and, in particular,
are non-negative, and, in particular,![]() . Hence
. Hence![]() .
.
Now take![]() , let
, let ![]() and c be as defined in (19), and choose any vector
and c be as defined in (19), and choose any vector![]() . Since
. Since ![]() is of full rank,
is of full rank, ![]() is expressible as
is expressible as![]() , for
, for![]() . Since
. Since ![]() for all m,
for all m, ![]() can be selected such that
can be selected such that ![]() for all m. Let
for all m. Let![]() . Then
. Then![]() . ,
. ,
One may determine whether such a c exists by maximizing c over non-negative c and ![]() satisfying (18) and (19), and checking to see if the maximum is greater than zero. The above maximization may be done via the simplex algorithm. If
satisfying (18) and (19), and checking to see if the maximum is greater than zero. The above maximization may be done via the simplex algorithm. If![]() , then (18) and (19) are satisfied by the vector
, then (18) and (19) are satisfied by the vector ![]() with zeros in each component except that corresponding to
with zeros in each component except that corresponding to![]() ; this realization makes optimization of c more efficient. If the optimization indicates that such a positive c exists, the maximizer of (2) may be determined using Fisher scoring.
; this realization makes optimization of c more efficient. If the optimization indicates that such a positive c exists, the maximizer of (2) may be determined using Fisher scoring.
The second corollary follows directly from Theorem 1.
Corollary 2. Suppose that the random vector ![]() arises from the multinomial regression model (1) and (2). Use (7) to construct the implied conditional logistic regression model, and Theorem 1 to reduce the model to one with finite maximum likelihood estimates. Then standard asymptotic methods for conditional inference on model parameters of interest, including normal theory techniques and those of [1] , can be used for testing and estimation.
arises from the multinomial regression model (1) and (2). Use (7) to construct the implied conditional logistic regression model, and Theorem 1 to reduce the model to one with finite maximum likelihood estimates. Then standard asymptotic methods for conditional inference on model parameters of interest, including normal theory techniques and those of [1] , can be used for testing and estimation.
If either Corollary 1 or Corollary 2 indicates that finite maximum likelihood estimators do not exist, one might look for estimators in the extended real numbers![]() . In certain highly--structured cases, for example, when the sample space for certain stratified rank--based tests is embedded in a canonical exponential family [13] , unique maximizers in
. In certain highly--structured cases, for example, when the sample space for certain stratified rank--based tests is embedded in a canonical exponential family [13] , unique maximizers in ![]() can be show to exist. In general, unique estimators are known to exist in the extended real number only in the case when
can be show to exist. In general, unique estimators are known to exist in the extended real number only in the case when![]() , since the profile likelihood obtained by setting one of the parameters to
, since the profile likelihood obtained by setting one of the parameters to ![]() will correspond to the likelihood of a similar model, with one parameter, and one or more observations, deleted. This reduced regression model need not be of full rank, and so the profile likelihood need not have a unique maximizer. The second example, in Section 3, involves a sample space containing points for which (conditional) maximum likelihood estimates cannot be extended unambiguously, even if allowing infinite values for some components.
will correspond to the likelihood of a similar model, with one parameter, and one or more observations, deleted. This reduced regression model need not be of full rank, and so the profile likelihood need not have a unique maximizer. The second example, in Section 3, involves a sample space containing points for which (conditional) maximum likelihood estimates cannot be extended unambiguously, even if allowing infinite values for some components.
[9] motivates the penalized likelihood approach for estimation in order to reduce biases of estimators. Since the standard approach to estimation in this case allows for infinite estimators, expectations of the conventional estimators do not exist, and so bias is an inappropriate criterion for our estimator. In what follows, the median bias (that is, the difference between the median of the sampling distribution of the estimator, minus the true value of the parameter) is used to assess quality of estimation.
3. Results
The following date reflects the results of a randomized clinical trial testing the effectiveness of a screening procedure designed to reduce hepatitis transmission in blood transfusions [9] [14] . The clinical trial was divided into two time periods. The data may be summarized as in Table 1 [9] . Hepatitis outcome is modeled as a function of period (![]() for early, and
for early, and ![]() for late), screening treatment (
for late), screening treatment (![]() for standard, and
for standard, and ![]() for the new method), and the interaction between period and treatment (
for the new method), and the interaction between period and treatment (![]() ). The model also contains an intercept term (I). We treat the response as unordered categories.
). The model also contains an intercept term (I). We treat the response as unordered categories.
A log linear model is used, implying a comparison between each of the two hepatitis categories and the third no-disease baseline category. Each of these comparisons involves parameters for I, S, T, and![]() , for a total of 8 parameters. This model is saturated, in that there are as many parameters as there are potential table probabilities. In our case,
, for a total of 8 parameters. This model is saturated, in that there are as many parameters as there are potential table probabilities. In our case, ![]() ,
, ![]() for all m, and
for all m, and![]() .
.
The lack of any Hepatitis C cases among the treated individuals in the early period gives rise to infinite estimate for the T and ![]() parameters in the comparison between Hepatitis C and healthy subjects.
parameters in the comparison between Hepatitis C and healthy subjects.
In this simple case, closed-form maximizers of (2) under the alternative hypothesis exists, since the alternative hypothesis may be viewed as a saturated model for a ![]() table. No closed-form maximizers of (2) exist under the null hypothesis, since this model is equivalent to the model with no three-way interactions.
table. No closed-form maximizers of (2) exist under the null hypothesis, since this model is equivalent to the model with no three-way interactions.
The sampling distribution of the sufficient statistics is available in under the hypothesis that all six S, T, and
![]() coefficients are zero. Exact enumeration techniques may be used to enumerate all possible tables
coefficients are zero. Exact enumeration techniques may be used to enumerate all possible tables ![]() tables, and their probabilities [15] , under the assumption that treatment and time combinations are independent of disease status. There are 2,046,240 such tables.
tables, and their probabilities [15] , under the assumption that treatment and time combinations are independent of disease status. There are 2,046,240 such tables.
Inference on the two ![]() parameters may be performed by conditioning the distribution of the associated sufficient statistics for the interaction terms on sufficient statistics associated with the T, S, and I parameters. This conditioning is equivalent to conditioning on Hepatitis C and non-ABC Hepatitis totals for each treatment group, and each time period, separately. After performing this conditioning, 24 tables remain, with 6 distinct values for the effect of the
parameters may be performed by conditioning the distribution of the associated sufficient statistics for the interaction terms on sufficient statistics associated with the T, S, and I parameters. This conditioning is equivalent to conditioning on Hepatitis C and non-ABC Hepatitis totals for each treatment group, and each time period, separately. After performing this conditioning, 24 tables remain, with 6 distinct values for the effect of the ![]() interaction on Hepatitis C, and 4 distinct values for the effect of the
interaction on Hepatitis C, and 4 distinct values for the effect of the ![]() interaction on non-ABC hepatitis. This yields six tables for inference on the interaction effect on Hepatitis C, and four for inference on the interaction effect on non-ABC hepatitis. Figure 1 shows the median bias for estimation of the effect on Hepatitis C, indicating a small advantage for the uncorrected estimates. Figure 2 shows coverage of penalized likelihood asymptotic confidence intervals (17), and exact intervals (9), using (10). In this case, exact intervals are readily available, and have far better coverage properties than the asymptotic intervals; in particular, note that the asymptotic intervals have zero coverage for sufficiently large absolute values of the parameter of interest. Values presented in Figure 1 are summarized in Table 2, and values presented in Figure 1 are summarized in Table 3. The range presented in Table 2 are heavily dependent on the range of parameter values examined in Figure 1, and are intended only for comparison among the two methods.
interaction on non-ABC hepatitis. This yields six tables for inference on the interaction effect on Hepatitis C, and four for inference on the interaction effect on non-ABC hepatitis. Figure 1 shows the median bias for estimation of the effect on Hepatitis C, indicating a small advantage for the uncorrected estimates. Figure 2 shows coverage of penalized likelihood asymptotic confidence intervals (17), and exact intervals (9), using (10). In this case, exact intervals are readily available, and have far better coverage properties than the asymptotic intervals; in particular, note that the asymptotic intervals have zero coverage for sufficiently large absolute values of the parameter of interest. Values presented in Figure 1 are summarized in Table 2, and values presented in Figure 1 are summarized in Table 3. The range presented in Table 2 are heavily dependent on the range of parameter values examined in Figure 1, and are intended only for comparison among the two methods.
![]()
Figure 2. Coverage for various two-sided confidence interval procedures.
A second example concerns polling data related to British general elections [16] . The data set investigated here represents a subset of voters in one of eight geographic areas (London North, London South, Greater Manchester, Merseyside, South Yorkshire, Tyne and Wear, West Midlands, and West Yorkshire), and includes survey respondents who provided their ages and an informative response to a question measuring age at which education was finished (coded as 1 = 15 or younger, 2 = 16, 3 = 17, 4 = 18, 5 = 19 or older), and reported a party of preference, and party of intended vote in the 2005 election. Three parties (Conservative, Labor, and Liberal Democrat) were reported as answers to these last two questions. The resulting data set included 67 individuals. We model voting choice as a function of usual party preference and education, treated as an ordinal variable. In this case, ![]() , with covariates representing the effects of Labor and Liberal Democratic Party membership, and education, on the propensity to vote for Labor, and the same effects on the propensity to vote for the Liberal Democrats, plus intercept terms for Labor and Liberal Democrats. Membership in the Conservative Party, and choice of the Conservative Candidate, are taken as baseline. We explore the effect of education on the propensity to vote for the Labor candidates.
, with covariates representing the effects of Labor and Liberal Democratic Party membership, and education, on the propensity to vote for Labor, and the same effects on the propensity to vote for the Liberal Democrats, plus intercept terms for Labor and Liberal Democrats. Membership in the Conservative Party, and choice of the Conservative Candidate, are taken as baseline. We explore the effect of education on the propensity to vote for the Labor candidates.
The null distribution of this data set cannot be trivially expressed as the independence distribution for a contingency table. One might enumerate the conditional sample space for the sufficient statistics vectors of (3), and the associated conditional probabilities [17] ; this calculation, however, took over 16 hours to complete when coded in FORTRAN 90 and run on a 2.6 GHz processor with a 1 GB cache and 8 GB of memory, and is too intensive for routine use. This condition distribution is tabulated in Table 4. Figure 3 shows the median bias for estimates [8] and the proposed method, explicitly recognizing infinite estimates associated with the extreme points in the conditional sample space. While the median bias for both estimators is poor, the corrected estimator generally performed better than the uncorrected estimator, as reported by other authors.
This manuscript is primarily concerned with producing confidence intervals. One might use the asymptotic intervals calculated using the penalized likelihood (17), or (9), with probabilities calculated exactly using Table 4 in conjunction with (8) and the nominal level adjusted using (10), or (9), with cumulative probabilities approximated (in the present case using a double saddlepoint conditional distribution function approximation of [2] ). Table 5 shows the resulting confidence intervals, and Figure 4 shows the coverage of these intervals. As
![]()
Table 2. Median bias in two estimation methods for hepatitis data.
![]()
Table 3. Minimal coverage for two confidence interval methods for the hepatitis data.
![]()
Table 4. Probabilities ![]() of sufficient statistic associating education with labor party voting, conditional on sufficient statistics for other variables in model.
of sufficient statistic associating education with labor party voting, conditional on sufficient statistics for other variables in model.
![]()
Table 5. Two-sided confidence intervals for the effect of education on voting for labor candidate.
![]()
Figure 4. Coverage for various two-sided confidence interval procedures.
noted above, coverage for the asymptotic interval is zero for ![]() below the lowest possible confidence interval endpoint, and above the highest possible confidence interval endpoint; since each of these intervals is finite, and since there are only a finite number of these intervals, coverage is zero outside of a bounded interval for the penalized likelihood intervals (17). Coverage for the asymptotic saddlepoint interval is mostly quite good, except for one area in the middle. This poor performance near
below the lowest possible confidence interval endpoint, and above the highest possible confidence interval endpoint; since each of these intervals is finite, and since there are only a finite number of these intervals, coverage is zero outside of a bounded interval for the penalized likelihood intervals (17). Coverage for the asymptotic saddlepoint interval is mostly quite good, except for one area in the middle. This poor performance near ![]() can be attributed to the fact that for
can be attributed to the fact that for![]() , the saddlepoint confidence interval is shifted to the left relative to the exact interval, and so the saddlepoint interval
, the saddlepoint confidence interval is shifted to the left relative to the exact interval, and so the saddlepoint interval
![]()
Figure 5. Conditional sample space for education effects.
fails to cover some values of ![]() that the exact interval covers. See the first row in Table 5. Furthermore, this most extreme value of
that the exact interval covers. See the first row in Table 5. Furthermore, this most extreme value of ![]() has a considerable amount of conditional probability attached to it; see Table 4.
has a considerable amount of conditional probability attached to it; see Table 4.
In practice, Table 4, and hence the exact intervals in Table 5 and Figure 4, are not computationally feasible. The saddlepoint confidence intervals are computationally feasible, but when the entire sufficient statistic vector lies on the boundary of the convex hull of the sufficient statistic sample space, the methods of Corollary 2 are required to apply these methods.
One can also consider simultaneous inference on both education parameters. Figure 5 displays the conditional sample space for these the sufficient statistic vectors for the effects on education on preference for Labor and Liberal Democratic Candidates. Corollary 1 indicates that the observed sufficient statistic vector (indicated by W in the figure) corresponds to finite estimates. Note that the point indicated by Δ is an example of one corresponding to ambiguous estimates; the parameter associated with the first component is clearly estimated as![]() . The conditional likelihood associated with this sample space, with the first component of the parameter set to
. The conditional likelihood associated with this sample space, with the first component of the parameter set to![]() , corresponds to the sampling distribution consisting of only the point Δ; this space is degenerate, and any value for the second parameter is equally preferred. The point at the opposite corner of the parallelogram in Figure 5 exhibits similar behavior. Values presented in Figure 4 are summarized in Table 2, and values presented in Figure 5 are summarized in Table 3. The range presented in Table 2 are heavily dependent on the range of parameter values examined in Figure 4, and are intended only for comparison among the two methods.
, corresponds to the sampling distribution consisting of only the point Δ; this space is degenerate, and any value for the second parameter is equally preferred. The point at the opposite corner of the parallelogram in Figure 5 exhibits similar behavior. Values presented in Figure 4 are summarized in Table 2, and values presented in Figure 5 are summarized in Table 3. The range presented in Table 2 are heavily dependent on the range of parameter values examined in Figure 4, and are intended only for comparison among the two methods.
4. Conclusion
This paper presents an algorithm for converting a multinomial regression problem that features nuisance parameters estimated at infinity to a similar problem in which all nuisance parameters have finite estimates; this conversion is such that the distribution of a sufficient statistic associated with the parameter of interest, conditional on all other sufficient statistics, remains unchanged. These conditional probabilities in the reduced model may be approximated using standard asymptotic techniques to yield confidence intervals with coverage behavior superior to those that arise from, for example, asymptotics derived from the likelihood after penalizing using Jeffreys’ prior.
Acknowledgements
This research was supported in part by NSF grant DMS 0906569.