Received 11 December 2015; accepted 5 April 2016; published 8 April 2016

1. Introduction
For the past 40 years, chemical graph theory, as an important branch of both computational chemistry and graph theory, has attracted much attention and the results obtained in this field have been applied in many chemical and pharmaceutical engineering applications. In these frameworks, the molecular is represented as a graph in which each atom is expressed as a vertex and covalent bounds between atoms are represented as edges between vertices. Topological indices were introduced to determine the chemical and pharmaceutical properties. Such indices can be regarded as score functions which map each molecular graph to a non-negative real number. There were many famous degree-based or distance-based indices such as Wiener index, PI index, Zagreb index, atom-bond connectivity index, Szeged index and eccentric connectivity index. Because of its wide engineering applications, many works contributed to determining the indices of special molecular graphs (see Yan et al., [1] and [2] , Gao and Shi [3] and [4] , Xi and Gao [5] , Gao and Wang [6] - [8] , Gao and Farahani [9] , and Gao et al., [10] for more details).
In our article, we only consider simple (molecular) graphs which are finite, loopless, and without multiple edges. Let 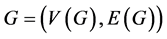 be a graph in which the vertex set and edge set are expressed as
be a graph in which the vertex set and edge set are expressed as 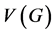 and
and , respectively. Here, each edge can be regarded as the subset of
, respectively. Here, each edge can be regarded as the subset of 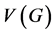 with exactly two elements, and edge set
with exactly two elements, and edge set 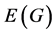 consists of all such edges. Readers can refer Bondy and Mutry [11] for any notations and terminologies used but not clearly explained in our paper.
consists of all such edges. Readers can refer Bondy and Mutry [11] for any notations and terminologies used but not clearly explained in our paper.
The first Zagreb index could be regarded as one of the oldest graph invariants which was defined in 1972 by Gutman and Trinajsti [12] as
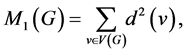
where 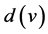 is the degree vertex v in G. Another alternative formulation for
is the degree vertex v in G. Another alternative formulation for 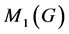 is denoted as
is denoted as
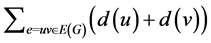 . And, the second Zagreb index was later introduced as
. And, the second Zagreb index was later introduced as

As degree-based topological indices, the multiplicative version of these Zagreb indices of a graph G is introduced by Gutman [13] , and Ghorbani and Azimi [14] as:

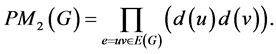
Here  is the first multiplicative Zagreb index and
is the first multiplicative Zagreb index and  is the second multiplicative Zagreb index. Several conclusions on these two classes of multiplicative Zagreb indices can be refered to Eliasi et al., [15] , Xu et al., [16] , and Farahani [17] and [18] .
is the second multiplicative Zagreb index. Several conclusions on these two classes of multiplicative Zagreb indices can be refered to Eliasi et al., [15] , Xu et al., [16] , and Farahani [17] and [18] .
There have been many advances in Wiener index, Szeged index, PI index, and other degree-based or distance- based indices of molecular graphs, while the study of the first and second multiplicative Zagreb index of special chemical structures has been largely limited. Furthermore, nanotube, nanostar and polyomino chain are critical and widespread molecular structures which have been widely applied in medical science, chemical engineering and pharmaceutical fields. Also, these structures are the basic and primal structures of other more complicated chemical molecular structures. Based on these grounds, we have attracted tremendous academic and industrial interests in determining the multiplicative Zagreb indices of special family of nanotube, nanostar and polyomino chain from a computation point of view.
The contribution of our paper is three-folded. First, we focus on four classes of nanotubes: ,
, ![]() , polyhex zigzag
, polyhex zigzag ![]() and polyhex armchair
and polyhex armchair![]() , and the multiplicative Zagreb indices of these four classes of nanotubes are determined. Second, we compute the multiplicative Zagreb indices of dendrimer nanostar
, and the multiplicative Zagreb indices of these four classes of nanotubes are determined. Second, we compute the multiplicative Zagreb indices of dendrimer nanostar![]() . At last, we calculate the multiplicative Zagreb indices of some special families of polyomino chains.
. At last, we calculate the multiplicative Zagreb indices of some special families of polyomino chains.
2. Multiplicative Zagreb Indices of Nanotubes
The purpose of this section is to yield the multiplicative Zagreb indices of certain special classes nanotubes. Our work in this part can be divided into two parts: 1) ![]() and
and ![]() nanotubes; 2) zigzag
nanotubes; 2) zigzag ![]() and armchair
and armchair![]() .
.
2.1. Nanotubes Covered by C5 and C7
In this subsection, we discuss ![]() and
and ![]() nanotubes which consisting of cycles
nanotubes which consisting of cycles ![]() and
and ![]() (or it is a trivalent decoration constructed by
(or it is a trivalent decoration constructed by ![]() and
and ![]() in turn, and thus called
in turn, and thus called ![]() -net). It can cover either a cylinder or a torus.
-net). It can cover either a cylinder or a torus.
The parameter p is denoted as the number of pentagons in the 1-st row of ![]() and
and![]() . The vertices and edges in first four rows are repeated alternatively. In these nanotubes, and we set q as the number of such repetitions. For arbitrary
. The vertices and edges in first four rows are repeated alternatively. In these nanotubes, and we set q as the number of such repetitions. For arbitrary![]() , there exist 16p edges and 6p vertices in each period of
, there exist 16p edges and 6p vertices in each period of ![]() which are adjacent at the end of the molecular structure. By simple computation, we check that
which are adjacent at the end of the molecular structure. By simple computation, we check that ![]() and
and ![]() since there are 6p vertices with
since there are 6p vertices with ![]() and other
and other ![]() vertices with
vertices with![]() .
.
Furthermore, there are 8p vertices and 12p edges in any periods of![]() . We get
. We get ![]() and
and ![]() since there are 5p vertices adjacent at the end of structure, and exists q repetition and 5p addition edges.
since there are 5p vertices adjacent at the end of structure, and exists q repetition and 5p addition edges.
Let ![]() and
and ![]() be the minimum and maximum degree of graph G, respectively. In the whole following context, for any graph G, its vertex set
be the minimum and maximum degree of graph G, respectively. In the whole following context, for any graph G, its vertex set ![]() and edge set
and edge set ![]() are divided into several partitions:
are divided into several partitions:
for any i, ![]() , let
, let![]() ;
;
for any j, ![]() , let
, let![]() ;
;
for any k, ![]() , let
, let![]() .
.
Therefore, by omitting the single carbon atoms and the hydrogen, we infer two partitions ![]() and
and ![]() for
for ![]() and
and![]() . Moreover, the edge set of
. Moreover, the edge set of ![]() and
and ![]() can be divided into the following three edge sets.
can be divided into the following three edge sets.
![]() (or
(or![]() ):
):![]() ;
;
![]() (or
(or![]() ):
):![]() ;
;
![]() (or
(or![]() ),
), ![]() and
and![]() .
.
Now, we state the main results in this subsection.
Theorem 1.
![]()
![]()
![]()
![]()
Proof. First, considering nanotubes ![]() for arbitrary
for arbitrary![]() . By analyzing its structure, we have
. By analyzing its structure, we have![]() ,
, ![]() ,
, ![]() and
and![]() . In terms of the definitions of multiplicative version of these Zagreb indices, we infer
. In terms of the definitions of multiplicative version of these Zagreb indices, we infer
![]()
![]()
Second, we consider nanotube ![]() for arbitrary
for arbitrary![]() . According to its chemical structure, we verify
. According to its chemical structure, we verify![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . Therefore, by means of the definitions of multiplicative version of these Zagreb indices, we get
. Therefore, by means of the definitions of multiplicative version of these Zagreb indices, we get
![]()
![]()
2.2. Two Classes of Polyhex Nanotubes
We study the multiplicative version of polyhex nanotubes: zigzag ![]() and armchair
and armchair ![]() in this sub- section. We use parameter
in this sub- section. We use parameter ![]() to denote the number of hexagons in the 1-st row of the
to denote the number of hexagons in the 1-st row of the ![]() and
and![]() . Analogously, the positive integer n is used to express the number of hexagons in the 1-st column of the 2D-lattice of
. Analogously, the positive integer n is used to express the number of hexagons in the 1-st column of the 2D-lattice of ![]() and
and![]() . In view of structure analysis, we conclude
. In view of structure analysis, we conclude ![]() and
and![]() .
.
Clearly, the degree of vertex in polyhex nanotubes can’t exceed three. For nanotubes ![]() with any
with any![]() , we infer
, we infer![]() ,
, ![]() ,
, ![]() and
and![]() . Moreover, for nanotube
. Moreover, for nanotube ![]() with any
with any![]() , we get
, we get![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Therefore, the results stated as follows are obtained by means of above discussions and the definitions of multiplicative Zagreb indices.
. Therefore, the results stated as follows are obtained by means of above discussions and the definitions of multiplicative Zagreb indices.
Theorem 2.
![]()
![]()
![]()
![]()
3. Multiplicative Zagreb Indices of Dendrimer Nanostars
Dendrimer is a basic structure in nanomaterials. In this section, for any![]() ,
, ![]() is denoted as the n-th growth of dendrimer nanostar. We aim to determine multiplicative Zagreb indices of dendrimer nanostar
is denoted as the n-th growth of dendrimer nanostar. We aim to determine multiplicative Zagreb indices of dendrimer nanostar ![]() (its structure can be referred to Figure 1 for more details).
(its structure can be referred to Figure 1 for more details).
This class of dendrimer nanostar has a core presented in Figure 1 and we call an element as a leaf. It is not difficult to check that a leaf is actually consisted of ![]() or chemically benzene, and
or chemically benzene, and ![]() is constituted by adding
is constituted by adding ![]() leafs in the n-th growth of
leafs in the n-th growth of![]() . Therefore, there are in all
. Therefore, there are in all ![]() leafs (
leafs (![]() ) in the dendrimer
) in the dendrimer![]() . The main contribution in this section can be stated as follows.
. The main contribution in this section can be stated as follows.
Theorem 3.
![]()
![]()
![]()
Figure 1. The structure of 2-dimensional of dendrimer nanostar![]() .
.
Proof. Let ![]() be the number of vertices with degree i (
be the number of vertices with degree i (![]() ) in
) in![]() . In terms of hierarchy structural of
. In terms of hierarchy structural of![]() , we deduce
, we deduce![]() ,
, ![]() and
and ![]() . Hence, by means of the induction on n with
. Hence, by means of the induction on n with![]() ,
, ![]() and
and![]() , we get
, we get ![]() and
and![]() .
.
Set![]() . We infer
. We infer
![]()
![]()
![]()
![]()
![]()
Therefore, the expected results are obtained by the definition of the first and the second multiplicative Zagreb index.
4. Multiplicative Zagreb Indices of Polyomino Chains
From the perspective of mathematical, a polyomino system can be considered as a finite 2-connected plane graph in which each interior cell is surrounded by a![]() . In other words, it can be regarded as an edge-connected union of cells in the planar square lattice. For instance, polyomino chain is a special polyomino system in which the joining of the centers (denoted
. In other words, it can be regarded as an edge-connected union of cells in the planar square lattice. For instance, polyomino chain is a special polyomino system in which the joining of the centers (denoted ![]() as the center of the i-th square) of its adjacent regular forms a path
as the center of the i-th square) of its adjacent regular forms a path![]() . Let
. Let ![]() be the set of polyomino chains with n squares. We have
be the set of polyomino chains with n squares. We have ![]() for each
for each![]() .
. ![]() is called a linear chain expressed as
is called a linear chain expressed as ![]() if the subgraph of
if the subgraph of ![]() induced by
induced by ![]() has exactly
has exactly ![]() squares. Moreover,
squares. Moreover, ![]() is called a zig-zag chain denoted as
is called a zig-zag chain denoted as ![]() if the subgraph of
if the subgraph of ![]() induced by
induced by ![]() (all the vertices with degree larger than two) is a path has exactly
(all the vertices with degree larger than two) is a path has exactly ![]() edges.
edges.
The branched or angularly connected squares in a polyomino chain are called a kink, and a maximal linear chain in a polyomino chain including the kinks and terminal squares at its end is called a segment represented by S. We use ![]() to denote the length of S which is determined by the number of squares in S. Assume a polyomino chain consists of a sequence of segments
to denote the length of S which is determined by the number of squares in S. Assume a polyomino chain consists of a sequence of segments ![]() with
with![]() , and we denote
, and we denote ![]() for
for ![]() with property that
with property that![]() . For arbitrary segment S in a polyomino chain, we have
. For arbitrary segment S in a polyomino chain, we have![]() . Specially, we get
. Specially, we get ![]() and
and ![]() for a linear chain
for a linear chain![]() , and
, and ![]() and
and ![]() for a zig-zag chain
for a zig-zag chain![]() .
.
The theorems presented in the below reveal clearly how the multiplicative Zagreb indices of certain families of polyomino chain are expressed.
Theorem 4. Let![]() ,
, ![]() be the polyomino chains presented above. Then, we get
be the polyomino chains presented above. Then, we get
![]()
![]()
![]()
![]()
Proof. The results are obvious for![]() , and we only focus on
, and we only focus on ![]() in the following discussion. It is not hard to check that
in the following discussion. It is not hard to check that![]() .
.
For the polyomino chain![]() , we obtain
, we obtain![]() ,
, ![]() and
and![]() . By the definitions of multiplicative Zagreb indices, we have
. By the definitions of multiplicative Zagreb indices, we have
![]()
![]()
By the same fashion, we yield
![]()
![]()
The expected results are got from the fact ![]() for
for![]() .
.
Theorem 5. Let ![]() (
(![]() ) be a polyomino chain with n squares and two segments which
) be a polyomino chain with n squares and two segments which ![]() and
and![]() . Then, we have
. Then, we have
![]()
![]()
Proof. For![]() , it is trivial. For
, it is trivial. For![]() , we obtain
, we obtain![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Therefore, by means of simply calculation, we obtain the desired results.
. Therefore, by means of simply calculation, we obtain the desired results.
Theorem 6. Let ![]() be a polyomino chain with n squares and m segments
be a polyomino chain with n squares and m segments ![]() (
(![]() ) such that
) such that ![]() and
and![]() . Then
. Then
![]()
![]()
Proof. For this chemical structure, we get![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Therefore, in view of the definitions of multiplicative Zagreb indices, we obtain the desired results.
. Therefore, in view of the definitions of multiplicative Zagreb indices, we obtain the desired results.
The last two results obtained using similarly tricks.
Corollary 1. Let ![]() (
(![]() ) be a polyomino chain with n squares and m segments
) be a polyomino chain with n squares and m segments ![]() (
(![]() ) such that
) such that![]() ,
, ![]() or
or![]() ,
,![]() . Then
. Then
![]()
![]()
Corollary 2. Let ![]() be a polyomino chain with n squares and m segments
be a polyomino chain with n squares and m segments ![]() (
(![]() ) such that
) such that ![]() (
(![]() ). Then
). Then
![]()
![]()
5. Conclusions and Further Work
The purpose of this paper is to discuss the multiplicative Zagreb indices of several chemical structures, and these molecular graphs we consider here are fundamentally and commonly used in chemical engineering. Spe- cifically, the contributions in this report can be concluded into three aspects: first, we compute the multiplicative Zagreb indices of four classes of nanotubes; then, the multiplicative Zagreb indices of dendrimer nanostars ![]() are calculated; at last, we also discuss some families of polyomino chains. As multiplicative Zagreb indices can been used in QSPR/QSAR study and play a crucial role in analyzing both the boiling point and melting point for medicinal drugs and chemical compounds, the results obtained in our paper illustrate the promising prospects of application for medical, pharmacal, biological and chemical sciences.
are calculated; at last, we also discuss some families of polyomino chains. As multiplicative Zagreb indices can been used in QSPR/QSAR study and play a crucial role in analyzing both the boiling point and melting point for medicinal drugs and chemical compounds, the results obtained in our paper illustrate the promising prospects of application for medical, pharmacal, biological and chemical sciences.
A closely related concept of the Zagreb index is the Estrada index (see Shang [19] and [20] for more details) and the techniques used in our paper can be potentially applicable to the Estrada indices. The Estrada index of special chemical graph structures can be considered in the further works.
Acknowledgements
We thank all the reviewers for their constructive comments in improving the quality of this paper. Research is supported partially by NSFC (No. 11401519).