Received 11 January 2016; accepted 5 April 2016; published 8 April 2016

1. Introduction
The Dutch windmill graph is denoted by  and it is the graph obtained by taking m copies of the cycle
and it is the graph obtained by taking m copies of the cycle 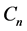 with a vertex in common. The Dutch windmill graph is also called as friendship graph if
with a vertex in common. The Dutch windmill graph is also called as friendship graph if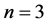 . i.e., friendship graph is the graph obtained by taking m copies of the cycle
. i.e., friendship graph is the graph obtained by taking m copies of the cycle 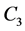 with a vertex in common. Dutch windmill graph
with a vertex in common. Dutch windmill graph 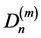 contains
contains 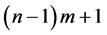 vertices and mn edges as shown in the Figures 1-3.
vertices and mn edges as shown in the Figures 1-3.
All graphs considered in this paper are finite, connected, loop less and without multiple edges. Let 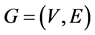 be a graph with n vertices and m edges. The degree of a vertex
be a graph with n vertices and m edges. The degree of a vertex 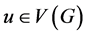 is denoted by
is denoted by 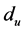 and is the number of vertices that are adjacent to u. The edge connecting the vertices u and v is denoted by uv. Using these terminologies, certain topological indices are defined in the following manner.
and is the number of vertices that are adjacent to u. The edge connecting the vertices u and v is denoted by uv. Using these terminologies, certain topological indices are defined in the following manner.
Topological indices are numerical parameters of a graph which characterize its topology and are usually graph invariants.
The atom-bond connectivity index, ABC index was one of the degree-based molecular descripters, which was introduced by Estrada et al. [1] in late 1990’s. Some upper bounds for the atom-bond connectivity index of
Definition 1.1. Let ![]() be a molecular graph and
be a molecular graph and ![]() is the degree of the vertex u, then ABC index
is the degree of the vertex u, then ABC index
of G is defined as,![]() .
.
The fourth atom bond connectivity index, ![]() index was introduced by M. Ghorbani et al. [9] in 2010. Further studies on
index was introduced by M. Ghorbani et al. [9] in 2010. Further studies on ![]() index can be found in [10] [11] .
index can be found in [10] [11] .
Definition 1.2. Let G be a graph, then its fourth ABC index is defined as, ![]() ,
,
where ![]() is sum of the degrees of all neighbours of vertex u in G. In other words,
is sum of the degrees of all neighbours of vertex u in G. In other words, ![]() , Similarly
, Similarly
for![]() .
.
The first and oldest degree based topological index was Randic index [12] denoted by ![]() and was introduced by Milan Randic in 1975.
and was introduced by Milan Randic in 1975.
Definition 1.3. For the graph G Randic index is defined as,![]() .
.
Sum connectivity index belongs to a family of Randic like indices. It was introduced by Zhou and Trinajstic [13] . Further studies on Sum connectivity index can be found in [14] [15] .
Definition 1.4. For a simple connected graph G, its sum connectivity index ![]() is defined as,
is defined as,
![]() .
.
The Geometric-arithmetic index, ![]() index of a graph G was introduced by D. Vukicevic et al. [16] . Further studies on GA index can be found in [17] - [19] .
index of a graph G was introduced by D. Vukicevic et al. [16] . Further studies on GA index can be found in [17] - [19] .
Definition 1.5. Let G be a graph and ![]() be an edge of G then,
be an edge of G then,![]() .
.
The fifth Geometric-arithmetic index, ![]() was introduced by A.Graovac et al. [20] in 2011.
was introduced by A.Graovac et al. [20] in 2011.
Definition 1.6. For a Graph G, the fifth Geometric-arithmetic index is defined as![]() ,
,
Where ![]() is the sum of the degrees of all neighbors of the vertex u in G, similarly for
is the sum of the degrees of all neighbors of the vertex u in G, similarly for![]() .
.
2. Main Results
Theorem 2.1. The Atom bond connectivity index of Dutch windmill graph is![]() .
.
Proof. Consider the Dutch windmill graph![]() . We partition the edges of
. We partition the edges of ![]() into edges of the type
into edges of the type ![]() where uv is an edge. In
where uv is an edge. In ![]() we get edges of the type
we get edges of the type ![]() and
and![]() . Edges of the type
. Edges of the type ![]() and
and ![]() are colored in red and black respectively as shown in the figure [18] . The number of edges of these types are given in the Table 1.
are colored in red and black respectively as shown in the figure [18] . The number of edges of these types are given in the Table 1.
We know that ![]()
i.e., ![]()
![]()
[From Table 1 and Figure 4]
![]()
□Theorem 2.2. The Randic Index of Dutch windmill graph is ![]() Proof. We know that
Proof. We know that ![]()
![]()
Table 1. Edge partition based on degrees of end vertices of each edge.
i.e., ![]()
![]() [From Table 1 and Figure 4]
[From Table 1 and Figure 4]
![]() . □
. □
Theorem 2.3. The Geometric-arithmetic index (GA) of Dutch windmill graph is
![]() .
.
Proof. We know that ![]()
![]()
![]() [From Table 1 and Figure 4]
[From Table 1 and Figure 4]
![]() . □
. □
Theorem 2.4. The Sum connectivity index ![]() of Dutch windmill graph is
of Dutch windmill graph is![]() .
.
Proof. We know that ![]()
i.e., ![]()
![]() [From Table 1 and Figure 4]
[From Table 1 and Figure 4]
![]() . □
. □
Theorem 2.5. The fourth atom bond connectivity index of Dutch windmill graph is
![]()
Proof. Any Dutch windmill graph ![]() contains
contains ![]() vertices and mn edges. Let
vertices and mn edges. Let ![]() denote the degree of the vertex u. We partition the edges of
denote the degree of the vertex u. We partition the edges of ![]() into edges of the type
into edges of the type ![]() where uv is an edge and
where uv is an edge and ![]() is the sum of the degrees of all neighbours of vertex u in G. In other words,
is the sum of the degrees of all neighbours of vertex u in G. In other words, ![]() , Similarly for
, Similarly for![]() .
.
Case (1) If![]() : In
: In ![]() we get edges of the type
we get edges of the type![]() ,
, ![]() and
and![]() . Edges of the type
. Edges of the type![]() ,
, ![]() and
and ![]() are colored in red, green and black respectively as shown in the figure [1] . The number of edges of these types are given in the Table 2.
are colored in red, green and black respectively as shown in the figure [1] . The number of edges of these types are given in the Table 2.
We know that ![]()
i.e., ![]()
[From Table 2 and Figure 5]
![]()
![]()
![]()
Table 2. Edge partition based on degree sum of neighbors of end vertices of each edge.
![]()
Case (2) If![]() : In
: In ![]() we get edges of the type
we get edges of the type ![]() and
and![]() . The number of edges of these types are given in the Table 3.
. The number of edges of these types are given in the Table 3.
We know that ![]()
i.e., ![]()
Theorem 2.6. The fifth Geometric-arithmetic index (![]() ) of Dutch windmill graph is
) of Dutch windmill graph is
![]()
Proof. We know that ![]()
Case (1) If![]() :
: ![]() [From Table
[From Table
2 and Figure 5]
![]()
![]()
Case (2) If![]() :
:
![]()
![]()
Table 3. Edge partition based on degree sum of neighbors of end vertices of each edge.
[From Table 3]
![]()
![]() . □
. □
3. Conclusion
The problem of finding the general formula for ABC index, ![]() index, Randic connectivity index, Sum connectivity index, GA index and
index, Randic connectivity index, Sum connectivity index, GA index and ![]() index of Dutch Windmill Graph is solved here analytically without using computers.
index of Dutch Windmill Graph is solved here analytically without using computers.
Acknowledgements
The first author is also thankful to the University Grants Commission, Government of India for the financial support under the grant MRP(S)-0535/13-14/KAMY004/UGC-SWRO.
Conflict of Interests
The authors declare that there are no conflicts of interests regarding the publication of this paper.