Received 18 February 2016; accepted 27 March 2016; published 31 March 2016

1. Introduction
Symmetries play an important role in physical laws. The field variables can change at different spacetime points, while their referring group elements are the functions of the spacetime coordinates. Such transformation is called gauge transformation, which determines in a considerable degree the interaction form. We get an idea from Yang-Mills theory that more elaborate symmetries are able to produce connection fields accounting for nature’s forces [1] . It is the symmetry that brings the electromagnetic force and weak interaction together in a single electroweak structure [2] - [5] , resulting in those particles without mass, which violates, however, our observed fact. Nambu and Goldstone thought that the Bardeen-Cooper-Schriffer (BCS) theory about superconductivity was an example of spontaneous symmetry-breaking applied to the gauge field of electromagnetism [6] [7] . Anderson pointed out that their suggestion only referred to global symmetries, that gauge symmetries were particular and that breaking didn’t leave any massless particles [8] . Higgs perceived that to obtain mass some sacrifices should be made, and the spontaneous symmetry breaking of massless particles would naturally emerge [9] .
In 1967-1968, a theory on weak and electromagnetic forces was set up by Weinberg and Salam [3] - [5] . Four scalar fields were put into this theory, three fields were built in giving mass the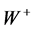 ,
,  , and
, and 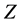 particles, the rest acted as a physical particle to manifest a bundle of the energy and momentum of this field. The new particle did be the Higgs bosons. The Higgs is a scalar boson and different from other gauge bosons. The Higgs field fills space here and there. A Higgs-like particle had been discovered at Conseil European pour la Recherche Nucleaire (CERN) in Geneva on 4 July 2012. We are now facing on a problem: What’s the Higgs field? We should figure out the relation between electroweak phase transition and the occurrence of the Higgs.
particles, the rest acted as a physical particle to manifest a bundle of the energy and momentum of this field. The new particle did be the Higgs bosons. The Higgs is a scalar boson and different from other gauge bosons. The Higgs field fills space here and there. A Higgs-like particle had been discovered at Conseil European pour la Recherche Nucleaire (CERN) in Geneva on 4 July 2012. We are now facing on a problem: What’s the Higgs field? We should figure out the relation between electroweak phase transition and the occurrence of the Higgs.
In general theory of relativity Einstein supposed that there was a standard clock at each spacetime point, this means that time can exist at everywhere and has an orientation at each point. An object in stationary state, in terms of classical physics, may have zero space coordinates, and has a straight trajectory known as the world line due to time is always flowing. The object has a proper energy, which reminds us that there is a certain relation between time and mass for the dual relationship of time and energy. We define the time orientation of today as its positive direction, the opposition, negative. The world we can touch is in the time ordered state with positive direction. There is not any boundary of the universe, one part of which is our world, which is so big that we may approximately consider it as infinite. It seems reasonable to suppose that in the evolution process of universe, with the decreasing of temperature our world underwent a phase transition of time, a kind of second order phase transition. Suppose that a relative stable world emerged after rapid expansion of universe, the temperature fallen down so slowly that we can build a uniform space in this circumstances. Because of that given two points in a metric space, we can always find disjoin open sets containing them [10] . The space, therefore, is described as a simple cubic with identical lattices, on each of which there allowed to be a time orientation state, taking either positive or negative. We call such structure time-lattice model. We know that a transformation from disordered state to ordered state for a lattice system can be studied using methods of equilibrium statistical mechanics. One of the simplest examples of such a system is that of a system involving two different types of states A and B. If we only consider the nearest neighbors interactions, Ising model is the one of the most typical example, which can be used to describe such system as lattice gases, binary alloys, etc [11] .
A time-lattice model is such a similar system, where state A represents positive time state (p-time state), and the state B does negative time state (n-time state). In Section 2, based on our successful approach to the simple cubic Ising model [12] - [14] , we put forward a theory about the time phase transition with fractal structures. The time fields are just the Higgs fields. The correlations of the relevant states lead to four types of Higgs, and there is only one type when the correlation length of the lattices becomes infinity. The mechanisms of the energy state for Higgs field, the occurrence of antiparticles and negative mass, symmetries and hierarchies are described. The critical temperature 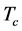 and the turning temperature
and the turning temperature 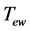 of the electroweak phase transition are also repre- sented. In Section 3, the energy density of the Higgs field and the time condensation are discussed. A possible mechanism of the formation of black hole is proposed. Section 4 is conclusion remark.
of the electroweak phase transition are also repre- sented. In Section 3, the energy density of the Higgs field and the time condensation are discussed. A possible mechanism of the formation of black hole is proposed. Section 4 is conclusion remark.
2. Theory
2.1. Time-Lattice Model
The Theory introduced and applied in reference [12] is a combination of the renormalization-group theory and the fractal geometry, in which topological analyses as a useful tool is adequately used. We describe here briefly how a simple cubic lattice system becomes ordered, more detail description including some more important equations can refer to this reference paper. There are infinite blocks in the system, a block shown in Figure 1 is divided into four identical sub-blocks. At the critical temperature 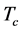 for the disordered-ordered transition the self-similar transformation makes the system become ordered. Such transformation shows that there are hierarchical structures: At first, some zero-order lattices (the original lattices) on the first hierarchy correlate to one another to form a 1-order sub-block with fractal dimension D. Four such sub-blocks then cooperate to build a 1-order ordered block with fractal dimension
for the disordered-ordered transition the self-similar transformation makes the system become ordered. Such transformation shows that there are hierarchical structures: At first, some zero-order lattices (the original lattices) on the first hierarchy correlate to one another to form a 1-order sub-block with fractal dimension D. Four such sub-blocks then cooperate to build a 1-order ordered block with fractal dimension 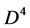 on the same hierarchy. An ordered block can be mapped into a 2-order lattice on the second hierarchy by the scaling law, and some 2-order lattices generate a 2-order sub-block, and four 2-order sub-blocks form a 2-order block on the same hierarchy…. A r-order ordered block of the r-th hierarchy, where r is a positive integer, shrinks into a (r + 1)-order lattice of the (r + 1)-th hierarchy, on which some (r + 1)-order lattices construct a (r + 1)-order sub-block. Four (r + 1)-order sub-blocks concert with each other to produce a (r + 1)-order block on the same hierarchy. When
on the same hierarchy. An ordered block can be mapped into a 2-order lattice on the second hierarchy by the scaling law, and some 2-order lattices generate a 2-order sub-block, and four 2-order sub-blocks form a 2-order block on the same hierarchy…. A r-order ordered block of the r-th hierarchy, where r is a positive integer, shrinks into a (r + 1)-order lattice of the (r + 1)-th hierarchy, on which some (r + 1)-order lattices construct a (r + 1)-order sub-block. Four (r + 1)-order sub-blocks concert with each other to produce a (r + 1)-order block on the same hierarchy. When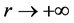 , the whole system is just a block, and finally the system becomes ordered.
, the whole system is just a block, and finally the system becomes ordered.
![]()
Figure 1. A block is divided into four identical sub-blocks.
Remember the correspondence relationship of the Ising model and the time-lattice model: The lattice spin-up state ® the p-time state of the lattice; the lattice spin-down state ® the n-time state of the lattice. The sub-block spin-up state ® the p-time state for the sub-block, the sub-block spin-down state ® the n-time state for it. The block spin-up state ® the p-time state for the block, the block spin-down ® the n-time for it. By using these correspondences we can directly understand the time phase transition while reading reference [12] - [14] .
2.2. Turning Temperature of the Electroweak Phase Transition and Higgs
It is the infinite iteration of the self-similar transformations at the  the system time becomes ordered on the infinite hierarchy. Meanwhile the correlation length of the original lattices is still finite because the block side n
the system time becomes ordered on the infinite hierarchy. Meanwhile the correlation length of the original lattices is still finite because the block side n
is finite. There exists a turning temperature  for the electroweak phase transition, and
for the electroweak phase transition, and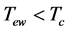 . There is not any sub-block or block if
. There is not any sub-block or block if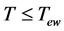 . In the temperature range
. In the temperature range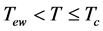 , there exist always sub-blocks and
, there exist always sub-blocks and
blocks. The lower the temperature is, the longer the correlation length of the lattices is, and the bigger the sizes of the sub-block and the block are. We have proved there are two sub-systems in the system: The sub-block sub-system and the block sub-system [12] . Four types of elementary excitations out of the harmonic waves of the relevant spin states may occur in the range  [13] [14] . The correlation of the lattices in the sub-block is responsible for the first type. The sub-blocks correlation for the second. The correlation of the lattices in the ordered block leads to the third. The blocks’ correlation to the fourth. The first type comes from two sorts of lattices correlations: One is the correlation of the original lattices, which are on the first hierarchy. Another is the correlation of the (r + 1)-order lattices within a (r + 1)-order sub-block,
[13] [14] . The correlation of the lattices in the sub-block is responsible for the first type. The sub-blocks correlation for the second. The correlation of the lattices in the ordered block leads to the third. The blocks’ correlation to the fourth. The first type comes from two sorts of lattices correlations: One is the correlation of the original lattices, which are on the first hierarchy. Another is the correlation of the (r + 1)-order lattices within a (r + 1)-order sub-block, ![]() , the (r + 1)-order lattices are just the r-order blocks on the r-th hierarchy, which are mapped to the lattices on the (r + 1)-th hierarchy through the scaling transformation [12] . When the temperature
, the (r + 1)-order lattices are just the r-order blocks on the r-th hierarchy, which are mapped to the lattices on the (r + 1)-th hierarchy through the scaling transformation [12] . When the temperature ![]() these four elementary excitations disappear and there is only one type of elementary excitation coming from the original lattices, which correlation length at this time becomes infinite. We think that each type of the elementary excitations represents a type of Higgs particles. Therefore, in the range
these four elementary excitations disappear and there is only one type of elementary excitation coming from the original lattices, which correlation length at this time becomes infinite. We think that each type of the elementary excitations represents a type of Higgs particles. Therefore, in the range ![]() there are four types of Higgs, and there is only one type if
there are four types of Higgs, and there is only one type if![]() . It is this type of Higgs that gives other particles mass. The Higgs originate from the correlation of the original lattices above mentioned. Three of Higgs in fact disappear, since the (r + 1)-order lattices come just from the r-order block
. It is this type of Higgs that gives other particles mass. The Higgs originate from the correlation of the original lattices above mentioned. Three of Higgs in fact disappear, since the (r + 1)-order lattices come just from the r-order block ![]() by the scaling law. The temperature
by the scaling law. The temperature ![]() is just the turning point for the electroweak phase transition.
is just the turning point for the electroweak phase transition.
2.3. Energy State
Let ![]() be the total number of “positive-positive” (p-p) nearest neighbor pairs for time,
be the total number of “positive-positive” (p-p) nearest neighbor pairs for time, ![]() the total number of “negative-negative” (n-n) nearest neighbor pairs for time. The p-p state and the n-n state are equivalent to the parallel spin coupling state with lower energy than that of the anti-parallel spin one, which is equivalent to the “positive-negative” (p-n) pair of the time states. From the point of view of the lattice states coupling, when the time is disordered, we have
the total number of “negative-negative” (n-n) nearest neighbor pairs for time. The p-p state and the n-n state are equivalent to the parallel spin coupling state with lower energy than that of the anti-parallel spin one, which is equivalent to the “positive-negative” (p-n) pair of the time states. From the point of view of the lattice states coupling, when the time is disordered, we have
![]() (1)
(1)
In this case the system energy is higher. When the system energy becomes lower than that of the disordered state, the situation turns over (the time shows global order), and
![]() (2)
(2)
This case is available for the range![]() . Such change of the energy demonstrates the characteristics of Higgs mechanism.
. Such change of the energy demonstrates the characteristics of Higgs mechanism.
2.4. Antiparticles and Negative Mass
Because of the duality relation of the time-energy for the system, the p-time state may relate to the positive energy state, the n-time state to the negative energy state. Dirac equation indicates that the negative energy state leads to antiparticles, which is equivalent to the n-time state as interpreted by Feynman. The infinite correlation length for the lattices doesn’t get rid of a chance in which the antiparticles happen in a short time within a small area. The global p-time state for the system is a subsequence of the correlation of the time states for all of individual lattices, but a simple addition of ones. Whenever there is locally a possibility of the n-time state in an area, where may appear antiparticles. This means that for the individual original lattices, the local symmetry SU(2) of the time state exists still. For the whole system, its time ordered state can select either positive or negative. If the state were negative, the relevant Higgs would give the particles negative mass. The occurrence of the antiparticles is of locality, and whether the mass takes positive or negative is dependent on the global time ordered state. That the antiparticle mass is as the same as the particle mass guarantees that Hamiltonian obeys CPT (charge conjugation, parity, and time reversal) symmetry, which can be proved by the following. Let ![]() be a state of a particle with mass
be a state of a particle with mass![]() , which equals the expectation value for its Hamiltonian
, which equals the expectation value for its Hamiltonian ![]() in the
in the![]() , and
, and
![]() (3)
(3)
The CPT unified operator is![]() ,
, ![]() , and
, and![]() , where
, where ![]() is an arbitrary phase factor. Under the operation of
is an arbitrary phase factor. Under the operation of![]() :
:
![]() (4)
(4)
The antiparticle mass in the state ![]() is given by
is given by
![]() (5)
(5)
Comparison of (4) and (5) illustrates that the Hamiltonian is invariant under the CPT operation:![]() .
.
2.5. Symmetries and Hierarchies
According to [12] , we get the fractal dimension D for a sub-block
![]() (6)
(6)
where n is the side of the sub-block, and its spin ![]() is given by
is given by
![]() (7)
(7)
![]() is the sub-block coordinate number, and
is the sub-block coordinate number, and![]() . The ordered block spin equals
. The ordered block spin equals
![]() (8)
(8)
where ![]() is the block coordinate number. When the side n takes a certain value, the spins
is the block coordinate number. When the side n takes a certain value, the spins ![]() and
and ![]() are constant. The conservation of the inner product for a sub-block spin or a block spin shows that the correlation obeys local symmetry
are constant. The conservation of the inner product for a sub-block spin or a block spin shows that the correlation obeys local symmetry ![]() (the spins can be in either spin-up state or spin-down state). In addition, the harmonic wave of the spin is governed by symmetry U(1) behaving in the way of plane wave [13] [14] . Therefore, we know there are symmetries in the range
(the spins can be in either spin-up state or spin-down state). In addition, the harmonic wave of the spin is governed by symmetry U(1) behaving in the way of plane wave [13] [14] . Therefore, we know there are symmetries in the range ![]() for the time-lattice model due to the correspondence of the model and the Ising model.
for the time-lattice model due to the correspondence of the model and the Ising model.
More complicated characteristics are that the hierarchies of these symmetries appear. Apparently, these symmetries show local gauge properties since the size of the sub-block and the block are finite. When the correlation length of the original lattices is of infinity the sub-blocks and the blocks disappear, the local symmetry ![]() of the three types of elementary excitations, except the first type, spontaneously breaks down, and the symmetry U(1) still exists, represented by the Higgs field due to the infinite correlation of the original lattices time states (the first sort of the first type of elementary excitation). The local symmetry SU(2) for the individual original lattices exists still until the temperature decreases to absolute zero. Meanwhile, the electromagnetic field and the gravitowagnetic field behave in the long-distance interaction way [15] . It should be here emphasized that the gravitowagnetic field includes the gravitational field and the wagnetic field. Both of them are related to mass. We still call the quanta of the gravitowagnetic wave as gravitons.
of the three types of elementary excitations, except the first type, spontaneously breaks down, and the symmetry U(1) still exists, represented by the Higgs field due to the infinite correlation of the original lattices time states (the first sort of the first type of elementary excitation). The local symmetry SU(2) for the individual original lattices exists still until the temperature decreases to absolute zero. Meanwhile, the electromagnetic field and the gravitowagnetic field behave in the long-distance interaction way [15] . It should be here emphasized that the gravitowagnetic field includes the gravitational field and the wagnetic field. Both of them are related to mass. We still call the quanta of the gravitowagnetic wave as gravitons.
3. Discussion
The Higgs field is just the time field, which quanta are the Higgs particles. The temperature ![]() may be higher, and the vibration frequency of the field can be described by Einstein model involving a single frequency [16] . This means all of the Higgs particles have the same energy. Therefore, there is a correspondence between the mass and the particle energy. While the temperature decreases significantly down we should consider Debye model, including different frequencies. Instead of a unique energy, the particles should have different energies, and the above one-to-one relation of the mass and the energy will not hold.
may be higher, and the vibration frequency of the field can be described by Einstein model involving a single frequency [16] . This means all of the Higgs particles have the same energy. Therefore, there is a correspondence between the mass and the particle energy. While the temperature decreases significantly down we should consider Debye model, including different frequencies. Instead of a unique energy, the particles should have different energies, and the above one-to-one relation of the mass and the energy will not hold.
Using Debye theory [11] , we get the energy density at the temperature T for the Higgs field
![]() (9)
(9)
where ![]() is mean energy of the field, v is the Higgs wave propagating velocity, V the field volume,
is mean energy of the field, v is the Higgs wave propagating velocity, V the field volume, ![]() Plank constant,
Plank constant, ![]() Boltzmann constant,
Boltzmann constant, ![]() ,
, ![]() the angle frequency,
the angle frequency, ![]() the Debye temperature. Referring to [13] , we can explore the time condensation when
the Debye temperature. Referring to [13] , we can explore the time condensation when![]() . Let
. Let ![]() denote a total number of the Higgs,
denote a total number of the Higgs, ![]() denote a number of Higgs in excitation states; and
denote a number of Higgs in excitation states; and ![]() if
if![]() , i.e. there is neither p-n pair nor n-n pair for the lattices. Let
, i.e. there is neither p-n pair nor n-n pair for the lattices. Let ![]() be a time-ordered intensity at the temperature T,
be a time-ordered intensity at the temperature T, ![]() be the intensity at absolute zero. A relative intensity
be the intensity at absolute zero. A relative intensity ![]() is given by
is given by
![]() (10)
(10)
Notice that there is neither sub-block nor block, only original lattices. In a low temperature region, when![]() , the relative intensity becomes
, the relative intensity becomes
![]() (11)
(11)
where ![]() is constant. Since the Higgs particles are bosons, when the temperature decreases to a turning point of Bose-Einstein Condensation (BEC), the Higgs as a strong degeneration condition become so significant that the system properties will change dramatically different from that at the temperature
is constant. Since the Higgs particles are bosons, when the temperature decreases to a turning point of Bose-Einstein Condensation (BEC), the Higgs as a strong degeneration condition become so significant that the system properties will change dramatically different from that at the temperature![]() , we call the turning point as critical temperature
, we call the turning point as critical temperature ![]() of BEC, which is
of BEC, which is
![]() (12)
(12)
where![]() , m an effective mass,
, m an effective mass, ![]() is a Rieman zeta function. The ratio of
is a Rieman zeta function. The ratio of ![]() to
to ![]() is written as
is written as
![]() (13)
(13)
The relative intensity changes into
![]() (14)
(14)
The lower the temperature, the weaker the time liquidity, since more Higgs particles will pull up together in the condensation state. A subsequence of the effect is the time rhythm slow down, all of physical processes will slow their steps.
![]()
Figure 2. A continuous nonvanishing time vector field in a solid torus.
If the temperature![]() , the field energy density is represented by [11]
, the field energy density is represented by [11]
![]() (15)
(15)
where![]() , and
, and![]() . This means that with the decreasing of the temperature a
. This means that with the decreasing of the temperature a
space volume, even though it is small, will be full of the releasing energy of the Higgs, and the mass density, by the formula![]() , will become extremely big. Although we suppose the model is infinite, we only can, however, describe a finite world because our limited knowledge.
, will become extremely big. Although we suppose the model is infinite, we only can, however, describe a finite world because our limited knowledge.
If we consider the model as big but finite, the consequence of the time condensation may be shown as Figure 2 due to its possible boundary effect. The model will distort to become a solid torus, where there is a continuous nonvanishing time vector field. Clearly, there is neither starting point, nor terminal point for the time. The super strong gravitowagnetic field due to the extreme big mass will attract all of extraneous substances and tear them in pieces. Maybe, this is a possible mechanism of the formation of black hole.
The condensations make the Higgs particles pull up together to release partly their freedom degrees, and the massless particles such as the photons and the gravitons get a chance to become massive and slow down their speeds. Meanwhile, the particles may change their propagation paths.
4. Conclusion Remark
It is the most important to investigate all possible structures for the spacetime, which will provide us symmetries for the understanding of our world. From Equations (6) and (8), we know that the inner space of a block has about ![]() dimensions if the block side n tends close to infinity near
dimensions if the block side n tends close to infinity near![]() . Such a high dimensional space contains a lot of symmetries to leave much more rooms for exploration of unknown particles, and allow some useful analyses of the string theory to be transplanted to the model. The model can return to the original 3-di- mensional space by scaling law when
. Such a high dimensional space contains a lot of symmetries to leave much more rooms for exploration of unknown particles, and allow some useful analyses of the string theory to be transplanted to the model. The model can return to the original 3-di- mensional space by scaling law when![]() . This advantage manifests that the model is more applicable to describe our real world.
. This advantage manifests that the model is more applicable to describe our real world.