Received 3 January 2016; accepted 28 March 2016; published 31 March 2016

1. Introduction
The investigation of the properties for finite nucleus in its excitation state is very useful for understanding the products in heavy collision, barrier heights or saddle point configuration in nuclear fission. The Hartree-Fock (HF) theory [1] - [3] and more elaborate self-consistent theories [4] [5] have been widely and successfully applied to investigate various properties of nuclear structure.
One of the recent developments in the study of relativistic heavy-ion collisions is the identification of D-rich nuclear systems. When the nuclear system is compressed by heavy-ion collision experiments, the Ds may constitute up to 10% of nuclear constituents [6] - [8] .
In our earlier work, the excitation of D-degree freedom in 90Zr nucleus in (CSHF) was investigated [9] , where the ground state properties of 90Zr nucleus were examined in small model space that consisted of six major oscillator shells for N and six orbits for D. The goal of this work is to reexamine these properties in large model space that consists of nine oscillator shells for N and ten orbits for D.
The D isobar is an important mode of nucleonic excitation [10] [11] . It is due to a resonance in pion-nucleon scattering, photopion and electropion production from nucleon. In nuclear structure, the D resonance is an agent for corrections in the traditional picture of the nucleus as a system of nucleons only [12] [13] . It is as a considered constituent of nucleus beside nucleons. The D isobar provides a mechanism for pion scattering, pion production, and pion absorption [14] .
The theory of effective operators plays an important role in the modern approach to nuclear structure. The detailed calculations in Refs. [9] [15] - [18] demonstrated the effective Hamiltonian, Heff, and the calculation procedures in Refs. [19] - [22] . Based on the study presented in Ref. [9] , the two-body matrix elements are scaled in the N-N sector to an optimal value of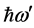 , the oscillator energy for 90Zr nucleus in the nine major oscillator shells with the ten delta orbits [19] - [22] . By using adjusting parameters:
, the oscillator energy for 90Zr nucleus in the nine major oscillator shells with the ten delta orbits [19] - [22] . By using adjusting parameters: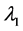 ,
, 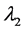 , and
, and 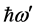 it is possible to obtain such a fit to the equilibrium binding energy and
it is possible to obtain such a fit to the equilibrium binding energy and 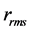 radius. In this work, the adjusting parameters:
radius. In this work, the adjusting parameters: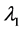 ,
, 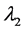 , and
, and 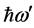 are: 0.999, 1.047, and 10.049, respectively.
are: 0.999, 1.047, and 10.049, respectively.
This paper is organized as follows: Section 2 specifies the results and discussions. Conclusions will be presented in Section 3.
2. Results and Discussion
In the previous studies [9] [23] - [25] , the following quantities were calculated: the Hartree-Fock energy, the root mean square radius, the number of delta particles in the occupied orbits, the radial density distribution, the single-particle energies, and the occupation probability of the single-particle orbits in the case of small model space. In this work, more detailed results for 90Zr nucleus are presented in order to examine its properties under static compression in larger model space consisting of nine major oscillator shells (excluding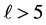 ) for nucleons and ten orbits for Ds making a total of 47 baryons orbits.
) for nucleons and ten orbits for Ds making a total of 47 baryons orbits.
2.1. The Hartree-Fock Energies
The bind energies 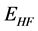 under compression using RSC potential are displayed in Figure 1 for 90Zr. The solid line represents results of the nucleon-only sector and the dashed line represents the results obtained when the Ds are added in the ten orbits:
under compression using RSC potential are displayed in Figure 1 for 90Zr. The solid line represents results of the nucleon-only sector and the dashed line represents the results obtained when the Ds are added in the ten orbits: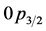 ,
, 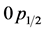 ,
, 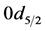 ,
, 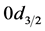 ,
, 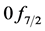 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Note that, in the CSHF approximation, the nucleons and delta may only mix in the
. Note that, in the CSHF approximation, the nucleons and delta may only mix in the![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() states.
states.
![]()
Figure 1. (CSHF ) energy as a function of the point mass ![]() for 90Zr is evaluated in 9 major oscillator shells with 10 D-orbits. The dashed curve corresponds to CSHF, the full calculations including the Ds, while the solid curve corresponding to CSHF with nucleons only.
for 90Zr is evaluated in 9 major oscillator shells with 10 D-orbits. The dashed curve corresponds to CSHF, the full calculations including the Ds, while the solid curve corresponding to CSHF with nucleons only.
Figure 1 clearly shows that there is virtually no difference in the results with and without Ds at equilibrium. It is seen that without the D-degree of freedom in the system, ![]() increases steeply towards zero binding energy under compression. When the transition to D is allowed, the nucleus remains bound as density is increased to 4.54 of normal density. Considering only the nucleons, the volume (based on the root mean square radius) of nucleus decreases by about 40% and the binding energy will be about 250.36 MeV with the inclusion of the D-excitations. In other words, this shows about 587.49 MeV, and 337.13 MeV of excitation energy to achieve a 40% volume reduction in the nucleon-only results, and nucleons and D+’s results, respectively.
increases steeply towards zero binding energy under compression. When the transition to D is allowed, the nucleus remains bound as density is increased to 4.54 of normal density. Considering only the nucleons, the volume (based on the root mean square radius) of nucleus decreases by about 40% and the binding energy will be about 250.36 MeV with the inclusion of the D-excitations. In other words, this shows about 587.49 MeV, and 337.13 MeV of excitation energy to achieve a 40% volume reduction in the nucleon-only results, and nucleons and D+’s results, respectively.
It appears from the above results that 337.13 MeV of excitation energy is enough to reduce the volume by 40% and the energy by 43% more. The results show that there is a significant reduction in the static compression modulus for RSC static compressions which is reduced by including the D excitations. The consequence of this reduction is the softening of the nuclear equation of state at larger compression. To see the role of D in determining the equation of state, Figure 1 shows the dependence of the ![]() on the compression charac- terized by the
on the compression charac- terized by the![]() . It can be seen that near equilibrium all curves agree. Also, the inclusion of D orbits tends to decrease of
. It can be seen that near equilibrium all curves agree. Also, the inclusion of D orbits tends to decrease of ![]() for compressed nuclei. The role of the Ds is less significant as the
for compressed nuclei. The role of the Ds is less significant as the ![]() approaches the ground state value.
approaches the ground state value.
Figure 1 shows that as the static load force increases, the compression of nucleus with nucleons only is less than the other nucleus with nucleons and Ds.
The difference between the results of the Hartree-Fock binding energy obtained in this work and those in Refs. [9] [23] - [25] is the size of the nucleon model space, the number of the D orbits included, different potentials and more compression. It is also worth mentioning that at equilibrium (no constraint) in 90Zr, it was not found any mixing between nucleon states and the D states. The same found in Refs. [9] [23] - [25] , all curves of ![]() are the same near equilibrium. This implies that results for the system at equilibrium don’t depend on model space. In comparison with results in previous studies [9] [23] - [25] , the current results are consistent with results obtained for 90Zr for
are the same near equilibrium. This implies that results for the system at equilibrium don’t depend on model space. In comparison with results in previous studies [9] [23] - [25] , the current results are consistent with results obtained for 90Zr for![]() . The results of the Hartree-Fock energy without compression and the behavior of curves for nucleons only and nucleons + Ds are the same for both the six and nine shells [9] . The static compression modulus is decreased significantly by increasing the nucleon model space. The current results display more compression than previous studies [9] [23] - [25] . It can be seen that the nuclear system becomes more compressible when the model space is increased. The results show that there is a significant reduction in the static compression modulus for RSC static compressions. It is reduced by including the D excitations. The consequence of this reduction is the softening of the nuclear equation of state at larger compression.
. The results of the Hartree-Fock energy without compression and the behavior of curves for nucleons only and nucleons + Ds are the same for both the six and nine shells [9] . The static compression modulus is decreased significantly by increasing the nucleon model space. The current results display more compression than previous studies [9] [23] - [25] . It can be seen that the nuclear system becomes more compressible when the model space is increased. The results show that there is a significant reduction in the static compression modulus for RSC static compressions. It is reduced by including the D excitations. The consequence of this reduction is the softening of the nuclear equation of state at larger compression.
In terms of relativistic heavy-ion collisions, the nucleus that can penetrate more easily when the D degree of freedom becomes explicit is implied by Figure 1. Because of the limitations of the model space, the calculations for higher densities are more speculative. Nevertheless it can give us some idea about how the D population can be increased as the nucleus is compressed to higher densities accessible to relativistic heavy-ion collisions.
2.2. The Number of D’s
Figure 2 shows the role of the D’s as a function of compression. The total number of D’s, D+’s and D0’s are plotted separately.
In Figure 2, the number of deltas increases rapidly as volume decreases. When the nucleus volume is reduced to about 78% of its volume at equilibrium, the number of deltas is increased to about 5.56% of all constituents of 90Zr. It is interesting to note in Figure 2 that the number of D0s and D+s are the same. In contrast to the previous findings [9] [24] , the curves of number for D+s and D0s don’t separate in the present work by increasing model space.
Although there is a rapid rise of the D-population as compression increases, the change in the total number of D’s does not exceed 0.0556 in Figure 2. Is this a reasonable amount of D population? To examine this issue, it is interesting to note that there is a consistency of the amount of N-D mixing with the amount of excitation energy exhibited with compression. That is, for example, when 0.0556D’s are presented, the excitation energy is in the order of 0.0556 (M-m) ≈ 16.52 MeV. Thus, on the scale of the unperturbed single-particle energies (including the rest mass of the nucleons and deltas), a substantial fraction of the compressive energy is delivered, through the N-D and D-D interactions to create more massive baryons in the lowest energy configuration of the nucleus. In other words, the number of D’s can be increased to about 5 at ![]() which corresponds to about 4.54 times the normal density.
which corresponds to about 4.54 times the normal density.
![]()
Figure 2. The number of D’s as a function of ![]() for 90Zr in 9 major shells model space. The upper curve is for the total number of D’s. The solid curve is for the number of D+, and the dashed curve is for D0.
for 90Zr in 9 major shells model space. The upper curve is for the total number of D’s. The solid curve is for the number of D+, and the dashed curve is for D0.
Figure 2 shows that the number of created Ds increases sharply when 90Zr nucleus compressed to a volume of about 0.78 of its equilibrium size. However, at this nuclear density, which is 4.54 times the normal density, the percentage of nucleons converted to D is only about 5.56% in 90Zr. This result is consistent with our previous results [9] and the results of relativistic heavy-ion collisions [6] - [8] [26] .
In comparison between our results with the previous results [23] [24] , the current results show the number of D’s is decreased by increased model space.
One potential consequence of this result is that it could represent a collective mechanism for Subthreshold pion production. That is, in subthreshold pion production experiments between colliding nuclei where the bom- barding energy per nucleon is below that needed to produce pions in N-N collisions. If the collisions produce isothermal compression, then the D’s are populated and relaxation could occur by the decay of the D to a nucleon and a pion. These calculations support a collective mechanism for subthreshold pion production.
2.3. The Radial Density Distributions
Figure 3 shows the radial density distributions for neutrons![]() , protons
, protons![]() , deltas
, deltas![]() , and their sum
, and their sum ![]() as a function of the radial distance from the center of the nucleus at large compression for 90Zr nucleus in a model space of nine major oscillator shells with D excitation restricted to the ten orbits:
as a function of the radial distance from the center of the nucleus at large compression for 90Zr nucleus in a model space of nine major oscillator shells with D excitation restricted to the ten orbits:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . The
. The ![]() is scaled by a factor of 10 to make it visible on the same scale as
is scaled by a factor of 10 to make it visible on the same scale as ![]() and
and![]() . In this figure, the neutron radial density is higher than the proton density at all values of r. This is due to Coulomb repulsion between the protons. The D-radial density distribution, under high compres- sion (point mass
. In this figure, the neutron radial density is higher than the proton density at all values of r. This is due to Coulomb repulsion between the protons. The D-radial density distribution, under high compres- sion (point mass![]() ), reaches a peak value of about 0.35 of the proton radial density at r = 2.80 fm. D-mixing with the nucleons in the
), reaches a peak value of about 0.35 of the proton radial density at r = 2.80 fm. D-mixing with the nucleons in the![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() orbits occurs and this explains the shape of the D-radial distribution presented in Figure 3.
orbits occurs and this explains the shape of the D-radial distribution presented in Figure 3.
Figure 4 displays the radial density distributions of 90Zr which is evaluated at about 0.16 reduced volume (![]() ). In this case, the D-radial density distribution reaches a peak value of around 0.47 of the proton radial density at 2.40 fm.
). In this case, the D-radial density distribution reaches a peak value of around 0.47 of the proton radial density at 2.40 fm.
In comparison between our results with the results of Ref. [9] , the radial density distribution for D is de- creased by increasing model space.
It can be seen from Figure 3, and Figure 4 that as compression increases, the total radial density increases and the radial density distribution of Ds increases sharply, whereas radial density of nucleons decreases sharply. This suggests that the less dense outer part of the nucleus initially responds to the external load more readily
than the inner part.
Clearly, the density in the interior rises relative to the interior density at equilibrium as the nucleus is com- pressed. This is in contrast to the behavior of the radial density on the outer-surface, where the radial density distribution is higher at equilibrium than the radial density when the static load is applied.
2.4. Single Particle Energies
Figure 5 displays the lowest self-consistent zero-change single particle energy levels as a function of![]() . The orbits curved up as the load on the nucleus increases. This is because the kinetic energy of the baryons which is
. The orbits curved up as the load on the nucleus increases. This is because the kinetic energy of the baryons which is
![]()
Figure 5. Single particle energy of lowest ten neutron states for 90Zr in nine-oscillator shells as a function of![]() .
.
a positive quantity becomes more influential than the attractive mean field of the baryons.
The single particle energies increase linearly after![]() , they intersect at higher compression especially for higher orbits, and consequently the nucleus becomes unbound. The behavior of single particle energies is independent of the model space [9] .
, they intersect at higher compression especially for higher orbits, and consequently the nucleus becomes unbound. The behavior of single particle energies is independent of the model space [9] .
The single particle energy spectrum also sees the gaps between the shells. As the nucleus is compressed, the single particle level ordering and gaps are preserved. The general trend exhibited the single particle energies (except the deepest bound orbital which actually drops with compression) shift to higher energies as the nucleus is compressed. The curvature goes up more and more as the orbital becomes closer to the surface. This implies that the surface is more responsive to compression than the interior of nucleus.
Moreover, single particle spectrum is generated entirely from the underlying microscopic Hamiltonian. This is a remarkable result since the calculated spectrum follows the expected ordering of the phenomenological shell model in the dominantly nucleons orbits. The spectrum also exhibits clearly visible gaps between the shells. As the nucleus is compressed, the single particle level ordering and the gaps are preserved. It is worth noting that the orbits closest to zero single-particle energy are more sensitive to compression. This means that these orbits are more responsive to compression than the interior orbits of nucleus. The general trend of single-particle energies exhibits a shift to higher energies as the nucleus is compressed.
The behavior of single particle energy levels is in good agreement with the orbital ordering of the standard shell model. The gap is very clear between the shells. The splitting of the levels in each shell is an indication that orbital-spin (L-S) coupling is strong enough in RSC potential, i.e., L-S coupling becomes stronger as the static load on the nucleus increases. When the nucleus is compressed, the splitting of the orbits becomes more noticeable especially in delta orbits.
3. Conclusions
The ground state properties of the neutron-rich spherical 90Zr nucleus have been investigated by using a realistic effective baryon-baryon Hamiltonian in the CSHF approximation. In model space consisting of nine major oscillator shells with D resonances of nucleons restricted to D orbits, the sensitivity of the results to the choice model space is examined.
It is found that the nuclear system becomes more compressible when the model space is increased. The radial density and the number of Ds are decreased by increasing model space. The behavior of single particle energies is found to be independent of the model space.
Future outlooks of this research are: we will increase the model space; a modified version of RSC should be used; thermal properties of finite nuclei can be incorporated in this model; a more general treatment should relax this restriction in order to allow for other mixing, e.g., (n, D−), (p, D++), (D0, D−), (D+, D++). Deformed nuclei can be studied by this model; relativistic effects can be also investigated and semi-classical descriptions of heavy-ion reaction at intermediate energies can be investigated.
Acknowledgements
The author acknowledges support for this research from the Deanship of Research at Zarqa University/Jordan.