On Two Extension Formulas for Lauricella’s Function of the Second Kind of Several Variables ()
Received 1 February 2016; accepted 27 March 2016; published 30 March 2016

1. Introduction
The Lauricella’s function  is defined and represented as follows [2]
is defined and represented as follows [2]
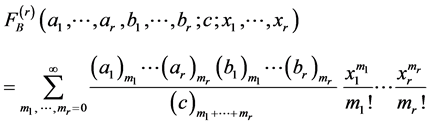 (1.1)
(1.1)
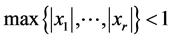 ;
;
where 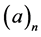 denotes the Pochhammer’s symbol defined by
denotes the Pochhammer’s symbol defined by
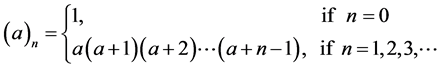 (1.2)
(1.2)
 (1.3)
(1.3)
Also, we note that
 (1.4)
(1.4)
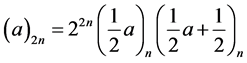 (1.5)
(1.5)
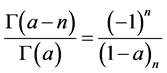 (1.6)
(1.6)
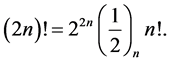 (1.7)
(1.7)
The generalized Lauricella’s function of several variables is defined as follows [2]
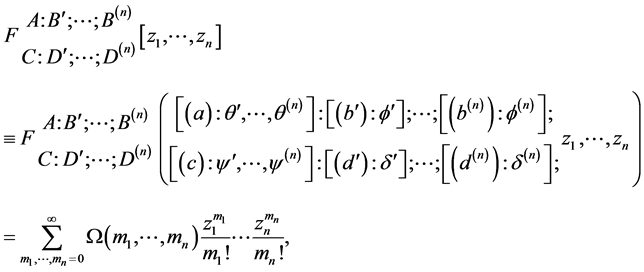 (1.8)
(1.8)
where
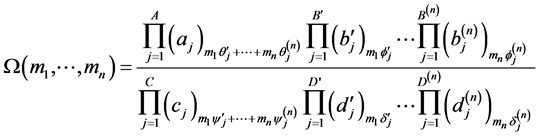 (1.9)
(1.9)
the coefficients 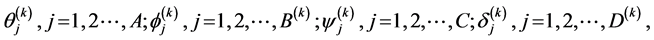 for all
for all
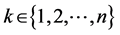 are real and positive;
are real and positive; ![]() abbreviates the array of A parameters;
abbreviates the array of A parameters; ![]() abbreviate
abbreviate
the array of ![]() parameters
parameters ![]() for all
for all ![]() with similar inter pretations for
with similar inter pretations for ![]() and
and ![]()
![]() . Note that, when the coefficients in Equation (1.8) equal to 1, the generalized Lauricella function (1.8) reduces to the following multivariable extension of the Kamp’e de F’eriet function [2] :
. Note that, when the coefficients in Equation (1.8) equal to 1, the generalized Lauricella function (1.8) reduces to the following multivariable extension of the Kamp’e de F’eriet function [2] :
![]() (1.10)
(1.10)
where
![]() . (1.11)
. (1.11)
In the theory of hypergeometric series, classical summation theorems such as Dixon, Watson and Whipple for the series![]() , have many generalizations and wide applications; see for example [1] [3] - [6] . In the present investigation, we shall require the following generalization of the classical Dixon’s theorem for the series
, have many generalizations and wide applications; see for example [1] [3] - [6] . In the present investigation, we shall require the following generalization of the classical Dixon’s theorem for the series ![]() [1] :
[1] :
![]() (1.12)
(1.12)
![]() ,
,
where ![]() denotes the greatest integer less than or equal to x and
denotes the greatest integer less than or equal to x and ![]() denotes the usual absolute value of x. The coefficients
denotes the usual absolute value of x. The coefficients ![]() are given respectively in [1] . When
are given respectively in [1] . When![]() , (1.12) reduces immediately to the classical Dixon's theorem [3] , (see also [6] )
, (1.12) reduces immediately to the classical Dixon's theorem [3] , (see also [6] )
![]() (1.13)
(1.13)
![]()
2. Extension Formulas
In this section, the following two extension formulas for Lauricella’s function of the second kind of several variables will be established:
![]() (2.1)
(2.1)
and
![]() (2.2)
(2.2)
where
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
for ![]()
The coefficients ![]() and
and ![]() can be obtained from the tables of
can be obtained from the tables of ![]() and
and ![]() given in [1] by replacing a by
given in [1] by replacing a by ![]() and
and ![]() respectively.
respectively.
Proof of (2.1): Denoting the left hand side of (2.1) by S, expanding ![]() in a power series and using the results [2] :
in a power series and using the results [2] :
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
![]() and
and![]() , (2.8)
, (2.8)
we get
![]() (2.9)
(2.9)
where
![]() (2.10)
(2.10)
Separating (2.9) into its even and odd terms, we have
![]() (2.11)
(2.11)
Finally, in (2.11) if we use the result (1.12), then we obtain the right hand side of (2.1). This completes the proof of (2.1). The result (2.2) can be proved by the similar manner.
3. Special Cases
1) In (2.1), if we take ![]() and use the results (1.3)-(1.7), then after some simplification we obtain the following transformation formula:
and use the results (1.3)-(1.7), then after some simplification we obtain the following transformation formula:
![]() (3.1)
(3.1)
which for![]() , reduces immediately to a known result of Bailey [7]
, reduces immediately to a known result of Bailey [7]
![]() (3.2)
(3.2)
where ![]() is Appell’s function [2] .
is Appell’s function [2] .
2) Similarly, in (2.2) if we take ![]() and use the results (1.3)-(1.7), then we obtain the following transformation formula:
and use the results (1.3)-(1.7), then we obtain the following transformation formula:
![]() (3.3)
(3.3)
3) In (2.2) if we take![]() , then we get a known extension formulas [8] for Lauricella’s function of three va-
, then we get a known extension formulas [8] for Lauricella’s function of three va-
riables ![]() for
for![]() .
.